Lyapunov-type Inequalities for a System of Nonlinear Di ff erential Equations

Wei Geng-ping

(Department of Mathematics,Huaihua University,Huaihua,Hunan,418008)

Lyapunov-type Inequalities for a System of Nonlinear Di ff erential Equations

Wei Geng-ping

(Department of Mathematics,Huaihua University,Huaihua,Hunan,418008)

Communicated by Shi Shao-yun

This paper presents several new Lyapunov-type inequalities for a system of first-order nonlinear di ff erential equations.Our results generalize and improve some existing ones.

Lyapunov-type inequality,nonlinear di ff erential equation,Hamiltonian system

1 Introduction

In this paper we are concerned the following system of nonlinear di ff erential equations:

whereα(t),β(t)andγ(t)are real-valued piece-wise continuous functions de fined onR,fandgare real-valued continuous functions de fined onR.

Ifandthen the system(1.1)reduces to the first-order linear Hamiltonian system

Note that(1.1)contains many well-known and well studied di ff erential equations as special cases.For example,the following second-order linear di ff erential equations can be written in form of(1.1)

and

wherep(t)andq(t)are real-valued piece-wise continuous functions de fined onRandρ(t)is a real-valued continuous function de fined onRwithρ(t)＞0.If we let

then(1.4)can be written in the form of(1.1)with

and

In 1907,Lyapunov[1]established the well known inequality which provides a lower bound for the distance between two consecutive zeroesa,bof the solution of the second-order linear di ff erential equation(1.3),namely

Since then many improvements on(1.6)have been developed and similar inequalities have been obtained for other types of di ff erential equations(see[2]and[3]).For instance, Wintner[4]showed that if(1.3)has a real solutionx(t)such that

then

where and in the sequelqwithMoreover,Wintner proved that the constant 4 cannot be replaced by a larger number.Later Hartman and Wintner[5]established

In 1969,Fink and Mary[6]extended Lyapunov inequality(1.8)to(1.4)and obtained the following Lyapunov-type inequality

In 2003,Yang[7]extended Lyapunov inequality(1.8)to the second-order di ff erential equation (1.5)and obtained the following inequality

if(1.5)has a solutionx(t)satisfying(1.7).In 2003,Guseinov and Kaymakcalan[8]further generalized(1.8)to the planar linear Hamiltonian system(1.2)and derived the following Lyapunov-type inequality

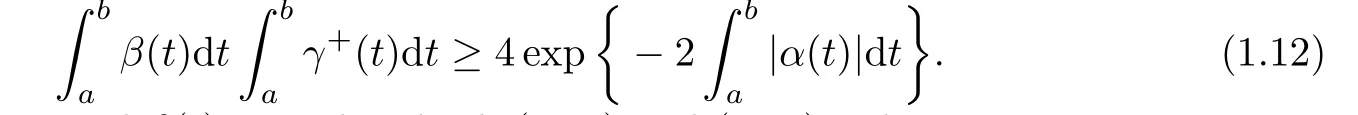
Note that ifα(t)=0 andβ(t)=1,then both(1.11)and(1.12)reduce to

which is almost identical to(1.8)except“＞”being replaced by“≥”.However,(1.11)and (1.12)do not include each other.Recently,Tanget al.[10]studied the following system

whereandand further generalized and improved(1.11)and(1.12).

Motivated by[8]–[10],in this paper,we aim to establish some new Lyapunov-type inequalities for system(1.1)and our results generalize/extend/improve some results mentioned above.In fact,The authors in[10]studied the system(1.14)which is a class of“superlinear”cases(i.e.,µ≥2 orν≥2).In this paper,we are concerned with the system(1.1),whereandare given functions that satisfyandfor allx=0 and are of linear growth at most.The system(1.1)is more general in the sense that nonlinearities are given by functionsfandgand therefore includes certain equations as special cases.Whenandour results are better than the results in[8] (See Remark 2.1).

2 Main Results

We first denote

Theorem 2.1Assume that

and there are constants M,m＞0such that

(1.1)has a solutionsatisfying(1.7).Then the following inequality

holds.

Proof.By(1.1),we obtain

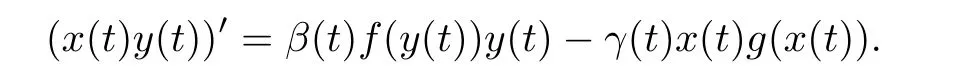
Integrating the above equation fromatoband taking into account thatx(a)=x(b)=0, we obtain

From the first equation of(1.1)and the fact thatx(a)=x(b)=0,we have

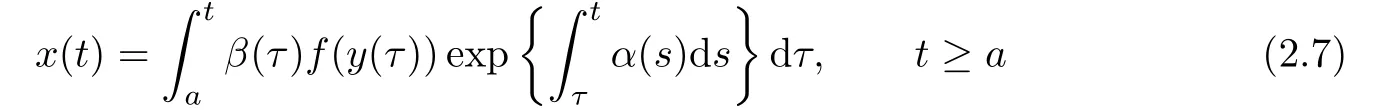
and

It follows from(2.1),(2.7)and the Cauchy inequality that

Similarly,it follows from(2.2),(2.8)and the Cauchy inequality that

By the condition that system(1.1)has a solutionsatisfying(1.7),we conclude that there exists asuch thatthus,orforFrom(2.9)and(2.10),we have

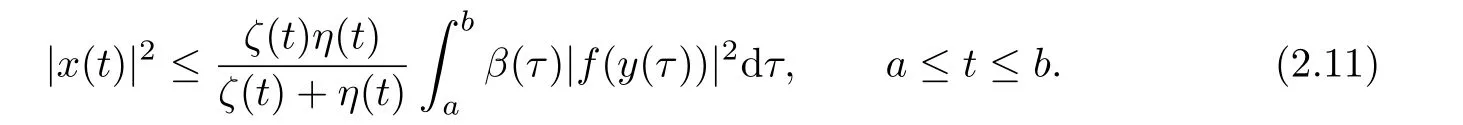
From(2.11)and(2.4),we obtain

Now,it follows from(2.6)and(2.12)that

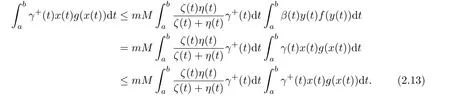
We claim that

If(2.14)is not true,then

From(2.6)and(2.15),we have

It follows from(2.4)that

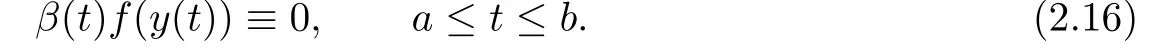
Combining(2.7)with(2.16),we obtain thatx(t)≡0 fora≤t≤b,which contradicts(1.7). Therefore,(2.14)holds.Hence,it follows from(2.13)and(2.14)that(2.5)holds.The proof is completed.

Theorem 2.2Assume that(2.3)and(2.4)hold.If(1.1)has a solution(x(t),y(t))satisfying(1.7),then there exists a c∈(a,b)such that

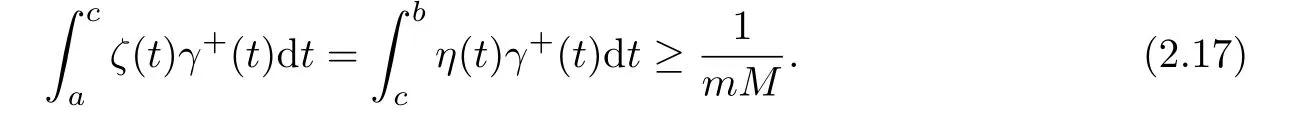
Proof.Choose ac∈(a,b)such that

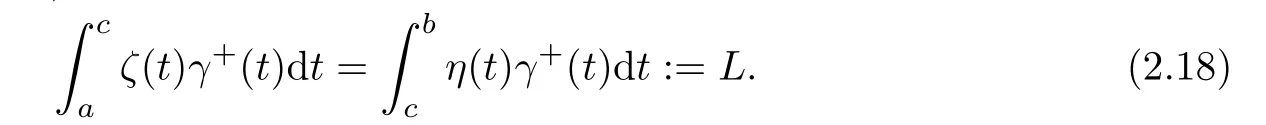
From(2.9)and(2.18),we have

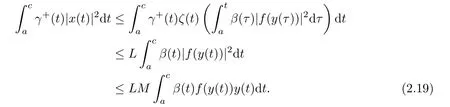
Similarly,we can obtain from(2.10)and(2.18)that

Adding(2.19)and(2.20),we have

It follows from

and(2.6)that

Corollary 2.1Suppose that hypothesis(2.3)and(2.4)are satis fied.If(1.1)has a solution(x(t),y(t))satisfying(1.7),then one has the following inequality

which implies that(2.23)holds.

Corollary 2.2Suppose that hypothesis(2.3)and(2.4)are satis fied.If(1.1)has a solutionsatisfying(1.7),then

Proof.By Theorem 2.2,we have

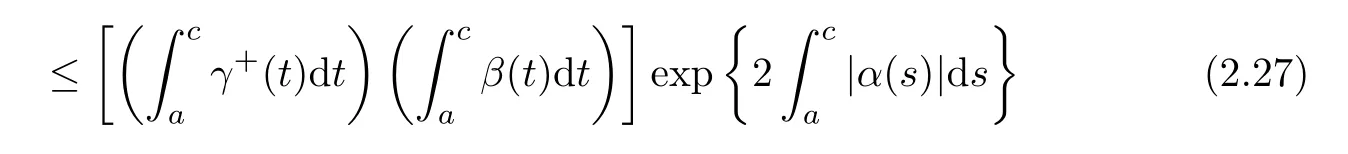
and

From(2.26)and(2.28),we have

and

From(2.27)and(2.29)–(2.31),we have

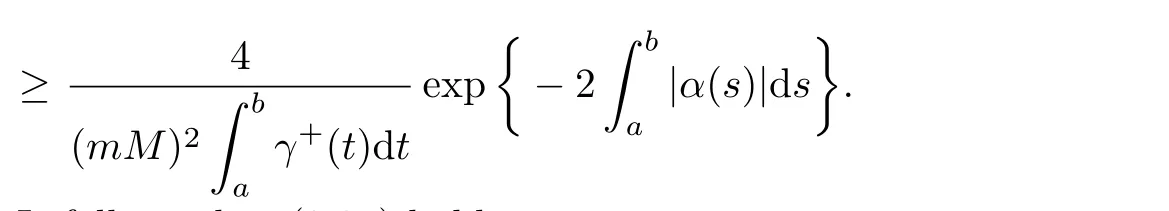
It follows that(2.25)holds.

Since

Corollary 2.3 follows from Corollary 2.1 or Corollary 2.2.

Corollary 2.3Suppose that hypothesis(2.3)and(2.4)are satis fied.If(1.1)has a solutionsatisfying(1.7),then

Remark 2.1It is easy to see that Lyapunov-type inequality(2.23)is better than(1.11) and(1.12)whenand

Note that inequalities(2.5),(2.23),(2.25),(2.29)and(2.32)are,in general,not strict. In case hypothesis(2.3)is replaced by the following stronger one

we further prove that inequalities(2.5),(2.23),(2.25),(2.29)and(2.32)are strict.

Theorem 2.3Suppose that(2.4)and(2.33)are satis fied.If(1.1)has a solution(x(t),y(t))satisfying(1.7),then one has the following inequality

where ζ(t)and η(t)are de fined by(2.1)and(2.2),respectively.

Proof.First,we prove that if hypothesis(2.3)is replaced by(2.33)in the proof of Theorem 2.1,then(2.11)is strict except end-pointsaandb,i.e.,

In fact,if(2.35)is not true,then there exists asuch that

Hence,from(2.9),(2.10)and(2.36),we obtain

and

It follows from(2.9)and(2.37)that

which implies that there exists a constantc1such that

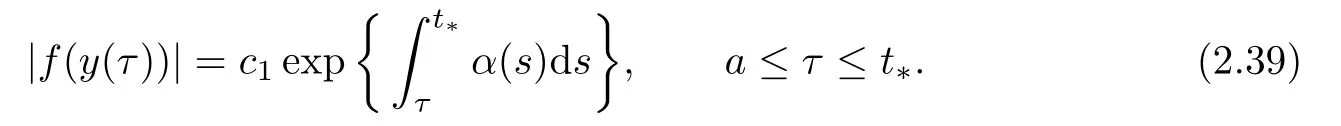
Similarly,It follows from(2.10)and(2.38)that there exists a constantc2such that

Sinceis continuous at(2.39)and(2.40)imply thatIfthenforit follows from(2.7)thatforwhich contradicts(1.8).Ifthenforit follows from(2.7) and(2.33)thatwhich contradicts the fact thatTherefore,(2.35)holds. Hence,in view of(2.35)and the proof of Theorem 2.1,(2.34)holds.The proof is completed.

In addition,in case Hypothesis(2.3)is replaced by(2.33)in the proof of Corollary 2.2, then(2.27)and(2.29)are also strict.Thus,we shall arrive to the following results which are immediate consequences of Theorem 2.3 and Corollaries 2.1–2.3.

Corollary 2.4Suppose that hypothesis(2.4)and(2.33)are satis fied.If(1.1)has a solutionsatisfying(1.7),then one has the following inequality

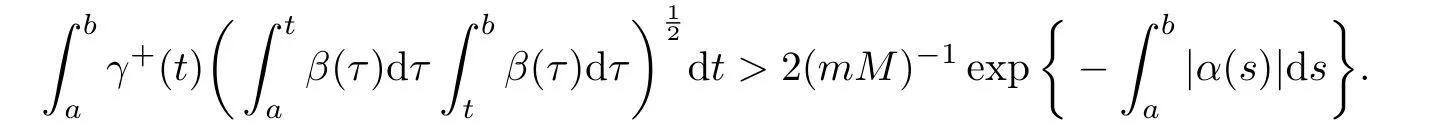
Corollary 2.5Suppose that hypothesis(2.4)and(2.33)are satis fied.If(1.1)has a solutionsatisfying(1.7),then

Corollary 2.6Suppose that hypothesis(2.4)and(2.33)are satis fied.If(1.1)has a solutionsatisfying(1.7),then

As application of our results,we consider the following system of di ff erential equations

whereα(t)is a real-valued continuous function de fined onR.It is easy to verify thatandsatisfy(2.4)withandforIf(2.41)has a solutionsatisfying(1.7),by Corollary 2.1 and notingwe have the following inequality

[1]Liapunov A M.Probl´eme g´en´eral de la stabilit´e du mouvement.Ann.Fac.Sci.Univ.Toulouse, 1907,2:203–407.

[2]Cheng S S.Lyapunov inequalities for di ff erential and di ff erence equations.Fasc.Math.,1991,23:25–41.

[3]Pachpatte B G.Mathematical Inequalities.North Holland Mathematical Library,67.Amsterdam:Elsevier,2005.

[4]Wintner A.On the non-existence of conjugate points.Amer.J.Math.,1951,73:368–380.

[5]Hartman P,Wintner A.On an oscillation criterion of Lyapunov.Amer.J.Math.,1951,73: 885–890.

[6]Fink A M,Mary D F St.On an inequality of Nehari.Proc.Amer.Math.Soc.,1969,21: 640–642.

[7]Yang X.On inequalities of Lyapunov type.Appl.Math.Comput.,2003,134:393–300.

[8]Guseinov G Sh,Kaymakcalan B.Lyapunov inequalities for discrete linear Hamiltonian systems.Comput.Math.Appl.,2003,45:1399–1416.

[9]Wang X.Stability criteria for linear periodic Hamiltonian systems.J.Math.Anal.Appl.,2010,367:329–336.

[10]Tang X H,Zhang Q M,Zhang M R.Lyapunov-type inequalities for the first-order nonlinear Hamiltonian systems.Comput.Math.Appl.,2011,62:3603–3613.

tion:34A40

A

1674-5647(2017)03-0205-10

10.13447/j.1674-5647.2017.03.02

date:Jan.27,2016.

The NSF(41405083,91437220)of China,and the NSF(2015JJ3098)of Hunan Province of China.

E-mail address:gengpingwei@163.com.