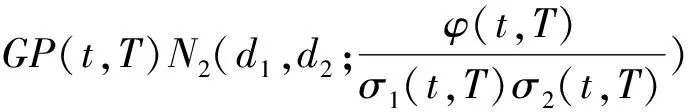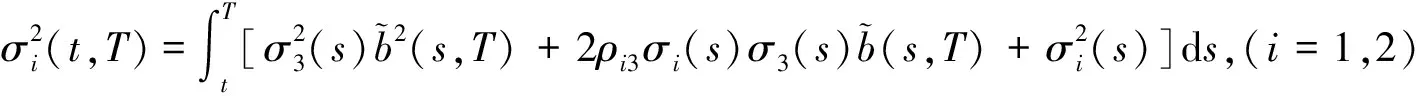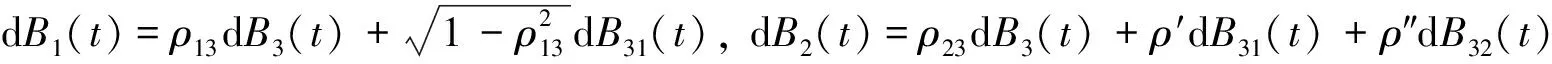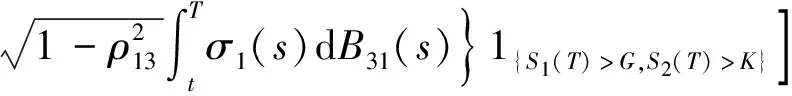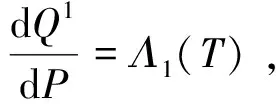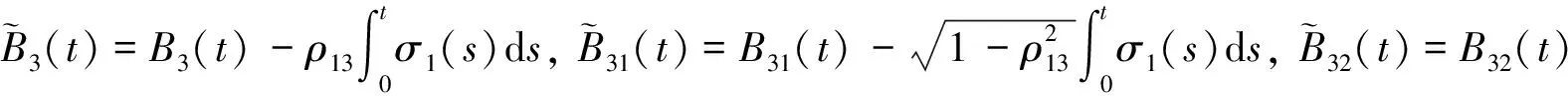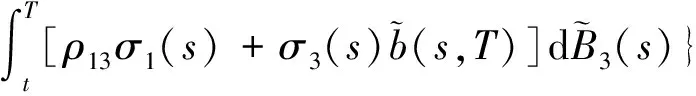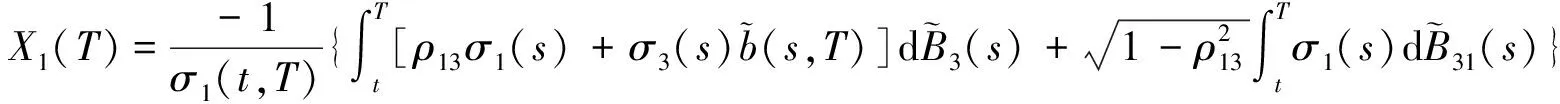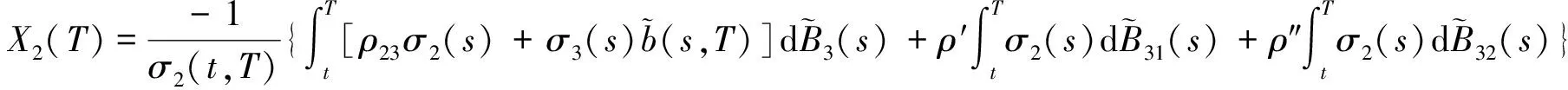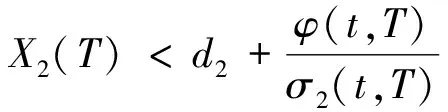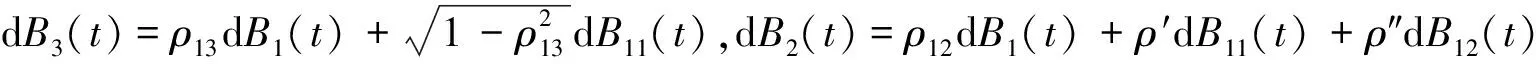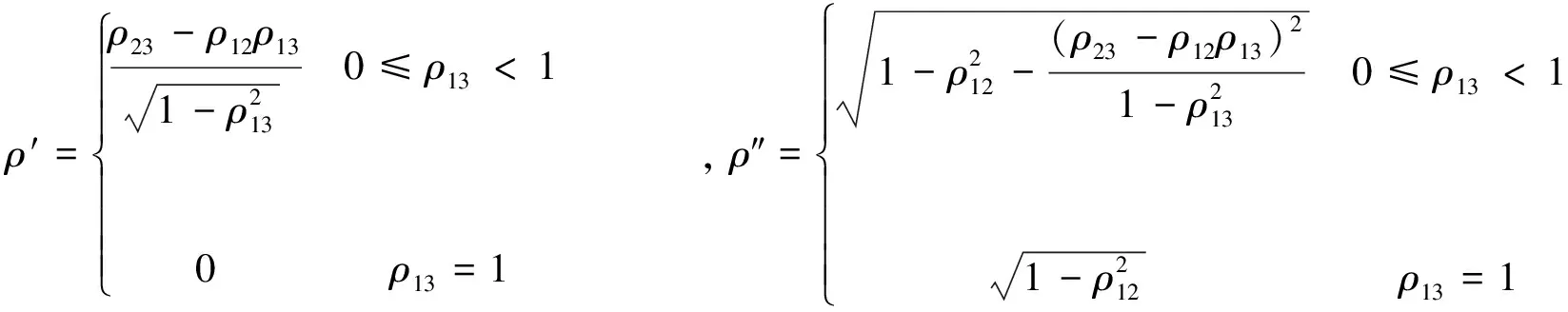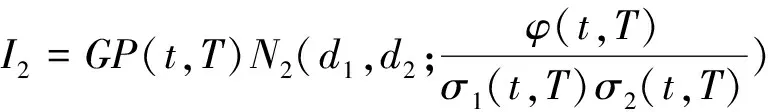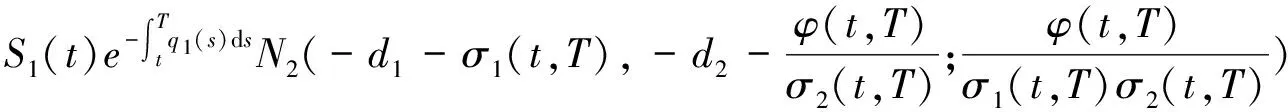随机利率下相关性数字期权的定价
康文娟, 李翠香
(河北师范大学 数学与信息科学学院,河北 石家庄 050024)
随机利率下相关性数字期权的定价
康文娟, 李翠香
(河北师范大学 数学与信息科学学院,河北 石家庄 050024)
利率随时间不断变化, 若假设利率服从Vasicek模型, 将更加贴近金融市场的实际情况.本文假设标的资产服从几何布朗运动, 利率服从Vasicek模型, 用多维Girsanov定理和测度变换推导出相关性数字期权的定价公式.
相关性数字期权; 测度变换; Girsanov定理
0 引 言
(1)
(2)
其中S1称为标的资产,S2称为测量资产,K为期权的执行价格,G为测量标的资产的缺口水平, 1A表示集合A的示性函数.由(1)(2)可以看出, 当S1=S2时, 即当S1与S2为同一资产时, 相关性数字期权即为缺口期权.
文献[2]给出了利率和红利均为常数的相关性数字期权的定价公式.由于在现实市场中, 利率是不断变化的, 所以许多学者扩展了B-S模型, 例如:2008年, 李淑锦[4]考虑了随机利率下欧式看涨期权和复合期权的定价.2012年, 张艳、周圣武[5]给出了随机利率下欧式缺口期权的定价公式.本文将研究利率服从Vasicek模型的相关性数字期权定价公式.
以下假设市场是均衡的, 完备的, 且无套利存在, 资产价格S1,S2满足随机微分方程(简称SDE):
dSi(t)=[r(t)-qi(t)]Si(t)dt+σi(t)Si(t)dBi(t),(i=1,2),
(3)
无风险利率r(t)服从扩展的Vasicek模型:
dr(t)=[a(t)-b(t)r(t)]dt+σ3(t)dB3(t),
(4)

1 预备知识
引理 1 设Si(t)满足SDE(3), 则对任意的t (5) 证明 由Ito公式得 对上式两边从t到T积分, 并整理得 引理1得证. 引理2[4]设无风险利率r(t)满足SDE(4), 则T时刻价值为{$1}的零息债券在t时刻的价格为 (6) 且 (7) 引理3 设Si(t)满足SDE(3), 则对任意的t (8) 证明 将(7)代入(5), 可得引理3. 引理4[3]设有界未定权益Y关于FT可测, 则在任意时刻t∈[0,T], 该未定权益的价值为 引理6[3]设W1(t),W2(t)为测度P下的独立的布朗运动, 若H1(t),H2(t)为平方可积的Ft可料过程, 则 是相互独立的布朗运动. 定理1 假设Si(t)和利率r(t)分别服从SDE(3)和(4), 则以S1(t)为标的资产,S2(t)为测量资产,K为执行价格,G为缺口水平, 到期日为T的欧式相关性数字看涨期权在到期前任意时刻t的价值为 其中N2(·,·;·)为二维正态分布累积函数, 证明 由引理4及(1)式知 C(S1(t),S2(t),t)=EP[e-∫Ttr(s)dsS1(T)1{S1(T)>G,S2(T)>K}]- GEP[e-∫Ttr(s)ds1{S1(T)>G,S2(T)>K}]=:I1+I2. (9) 首先计算I1.因为 (Bi(t),Bj(t))的相关系数为ρij(i,j=1,2,3且i≠j), 故在测度P下存在布朗运动B31(t),B32(t)使得B3(t),B31(t),B32(t)相互独立, 且 (10) 其中 由(5)及(10)知 I1=S1(t)e-∫Ttq1(s)dsEQ1[1{S1(T)>G,S2(T)>K}]=S1(t)e-∫Ttq1(s)dsQ1(S1(T)>G,S2(T)>K), (11) 且 (12) 是测度Q1下三个相互独立的布朗运动. 把(10)(12)代入(8)得 (13) (14) 由(11)得 (15) 其次计算I2.在测度P下存在布朗运动B11(t),B12(t)使得B1(t),B11(t),B12(t)相互独立, 且 (16) 其中 由(7)及(16)知 类似I1的证明可得 (17) 由(15)(17)知定理得证. 定理2 在定理1的条件下, 欧式相关性数字看跌期权在到期前任意时刻t的价值为 其中d1和d2同定理1. 证明 由引理4及(2)式知 P(S1(t),S2(t),t)=GEP[e-∫Ttr(s)ds1{S1(T) 类似于定理1中I1,I2的证明, 可得结论. [1]JohnC.Hull.Optionfuturesandotherderivatives[M].北京:机械工业出版社, 2011. [2]PeterG.Zhang.Exoticoptions[M].北京:机械工业出版社, 2014. [3]FimaC.Klebaner.Introductiontostochasticcalculuswithapplications[M].北京:人民邮电出版社, 2008. [4]李淑锦.随机利率下奇异期权的定价公式[J].数学学报, 2008,51(2):299-310. [5]张艳,周圣武,韩苗,等.随机利率Vasicek模型下的欧式缺口期权的定价研究[J].大学数学,2012, 28(4):98-101. [6]HullJC.Options,FuturesandOtherDerivatives(SeventhEdition)[M].北京:清华大学出版社, 2011. [责任编辑:王 军] Pricing of correlation digital options under the stochastic interest rate KANG Wenjuan, LI Cuixiang (College of Mathematics and Information Science of Hebei Normal University, Shijiazhuang 050024,China) Interest rate is changing with time, In order to make the asset prices model closer to reality of financial market, we will assume that the interest rate follows Vasicek model.In this paper, assuming that underlying asset price follows geometric Brownian motion, the interest rate follows Vasicek model, we get the pricing formulas of Correlation digital option by the help of multi-dimension Girsanov theorem and the change of measure. correlation digital option; measure transform;Girsanov’s theorem 2016-06-01 国家自然科学基金资助项目(11571089) 康文娟(1991—), 女, 河北赵县人, 河北师范大学硕士研究生, 主要从事金融数学的研究. O211.6 A 1672-3600(2017)06-0001-04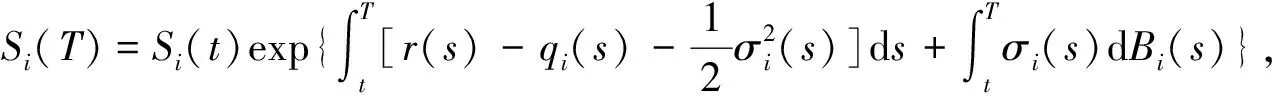
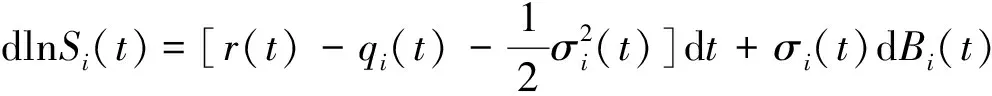
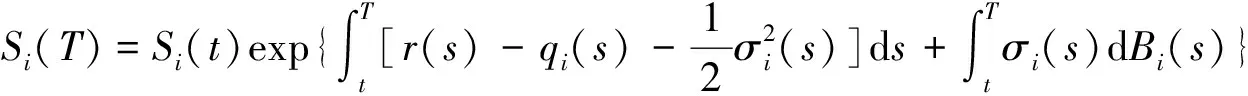
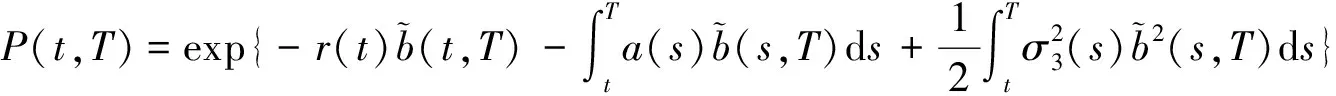

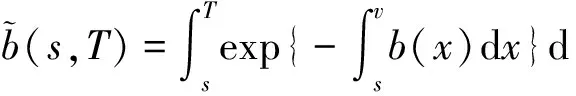
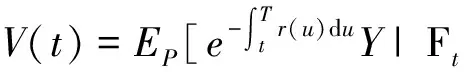



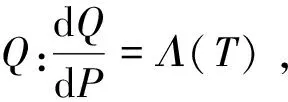

2 欧式相关性数字期权的定价