履带车辆扭矩载荷测试样本量的确定
刘海鸥, 赵梓烨, 徐 宜, 王 敏, 乔 丽
(1. 北京理工大学 机械与车辆学院, 北京 100081;2. 中国北方车辆研究所,北京 100072)
履带车辆扭矩载荷测试样本量的确定
刘海鸥1, 赵梓烨1, 徐 宜2, 王 敏2, 乔 丽2
(1. 北京理工大学 机械与车辆学院, 北京 100081;2. 中国北方车辆研究所,北京 100072)
扭矩载荷编谱技术是进行受载零部件机械结构设计和疲劳试验的重要研究基础.以某履带车辆传动轴为研究平台,以中值随机疲劳载荷谱编制原理和分散系数法定寿命原理为理论依据,提出了一种有较高置信度(90%以上)的样本量确定方法.通过设计扭矩测试及采集系统,获得了该履带车辆传动轴在典型行驶工况下的扭矩时域信号,依此确定了样本量的大小,并通过等效疲劳损伤原理进行了验证.该方法为编制履带车辆传动轴载荷谱提供了有效的原始数据,同时降低了试验样本数量及测试成本.
履带车辆;疲劳载荷谱;样本量确定;等效损伤;高置信度
对载荷谱编制方法研究的最根本目的就是要让其能最大限度地反映被测试件的实际受载情况,为零部件的设计提供真实可靠的设计基础,从P.Heuler[1]阐述了标准化的载荷时间历程,到C.M. Sonsino[2]提出了可变幅值的疲劳测试方法,再到Josef Morkus[3]描述了不同形式的载荷谱,机械动载行业逐渐形成了统一的载荷谱编制流程.尽管目前在航空、轮船、轨道等部分领域中载荷谱的编制工作已经比较成熟,但是由于测试设备和受载零部件的工作环境、使用强度的不同,载荷时间历程各有各的特点,所以针对不同试验应根据具体情况采取具有针对性的编谱方法.
传动系统在不同路面上的受载情况一直是被关注的核心和研究的热点,尤其是履带车辆不同于传统轮式车辆[4],由于其工作环境恶劣、空间狭小、工况负载变化多样,且变化瞬时速度快等给测试工作带来了极大的困难,一些特殊情况下的载荷瞬时出现难以捕获,所以履带车辆要想获得理想载荷数据需进行大量载荷试验.
载荷谱是进行车辆受载零部件机械结构设计和疲劳试验的基本依据,获得符合定寿设计原则的载荷谱则成为车辆零部件抗疲劳设计的重要前提.保证样本量充足,尽可能的涵盖全寿命周期下所有受载情况是最为核心的内容.
本次研究在确定样本最小样本量过程中,使用了中值随机疲劳载荷谱编制原理和分散系数法定寿原理作为理论基础[5],以真实试验数据作为编制载荷谱数据源,编制载荷谱,为进一步进行疲劳优化研究提供有效、直接的数据支撑.
1 分散系数法及中值载荷谱
对于像履带车辆这样的动力机械而言,其使用寿命是需要依靠全尺寸结构疲劳试验[6]进行确定的.试验中,疲劳试验机对结构施加的载荷谱真实性对疲劳寿命的确定至关重要.中值载荷谱理论的提出有效的解决了运用计数统计法[7-8]进行编谱时,对时间参量丢失的缺点.
1.1 技术路线
研究在原始数据的可靠性、有效性的基础上,为完成高效确定履带车辆传动系统载荷试验次数的目的,提出以下技术路线,如图1所示.
1.2 分散系数法

可以将N50中值疲劳寿命与Lf分散系数的比值定义为安全寿命Np[6].
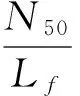
(1)
且假设对数疲劳寿命服从正态分布N(μ,σ),则对数安全疲劳寿命xp=lgNp可以写成:
xp=μ+up.
(2)

(3)
当已知母体的标准差σ的前提下,即σ=σ0,由上式可得(4),可求出理论分散系数Lf.
Lf=10-upσ0.
(4)
式中的标准正态偏量up是由不同可靠度P确定的,将Lf分散系数带入公式(1),即可获得安全寿命NP.以上依据试验数据先确定分散系数,再由分散系数确定零部件安全寿命的原理就是分散系数定寿原理.

图1 技术路线图
1.3 中值载荷谱的编制原理
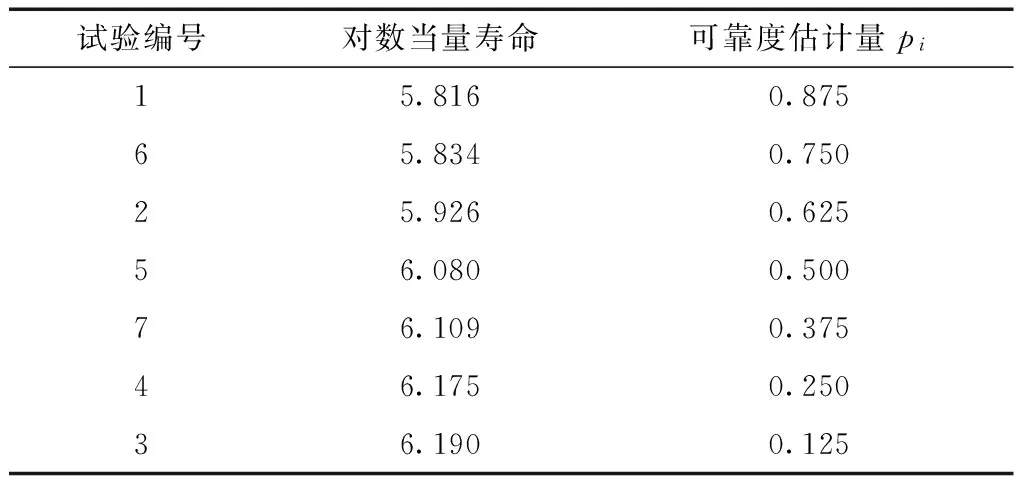
履带车辆在某工况下行驶,做循环试验n次,设第i次试验的当量寿命为Ti,则共取得n个观测值,则从小到大依次排列:
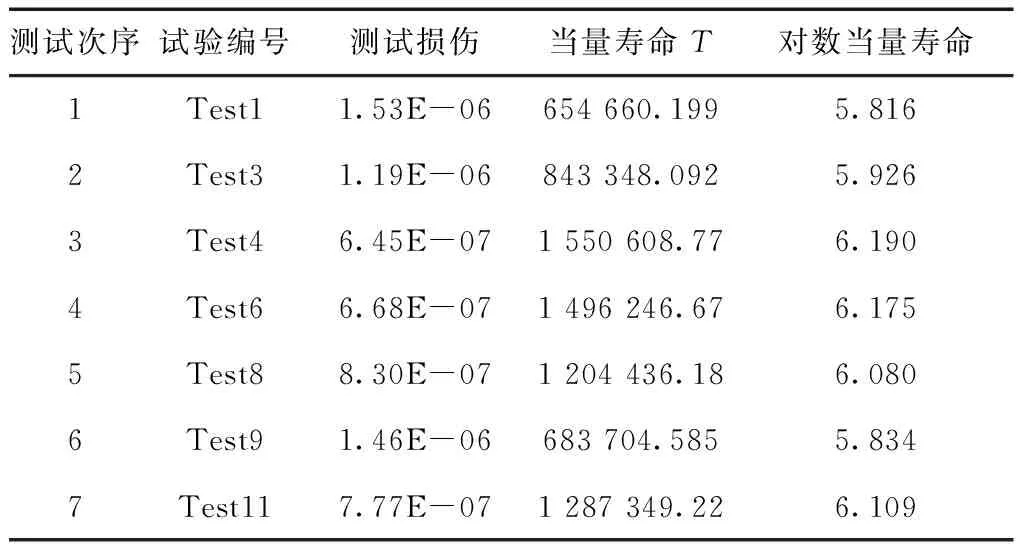
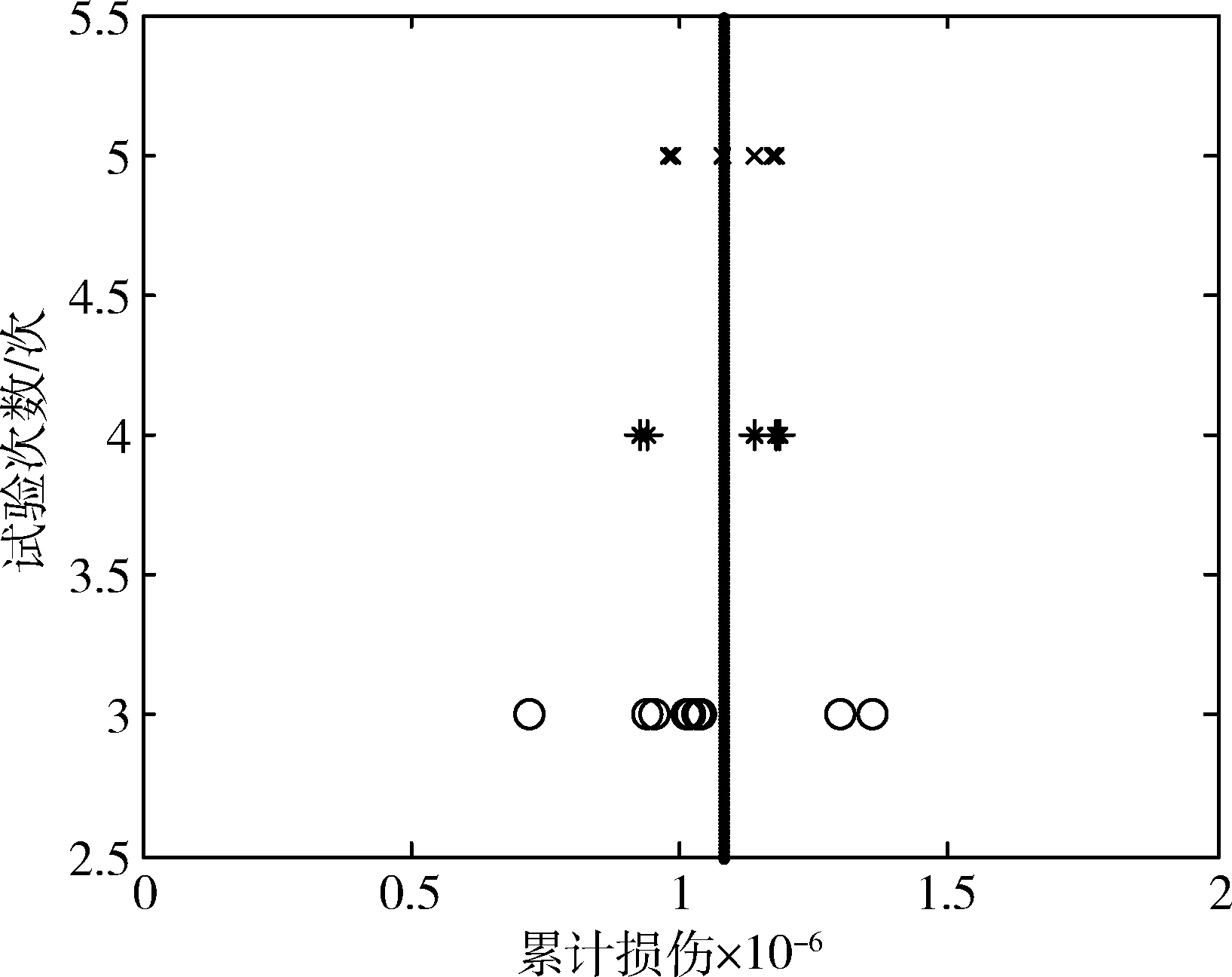
T1 第i个观测值Ti的可靠度估计量可由公式(5)确定. (5) i=0.5(n+1). (6) 由上式(6)可获得一组观测值中位于中间位置的数值序数.将居于中间位置的实测载荷—时间历程用于后续雨流计数、均幅值检验、极值推断、多工况合成等处理编制而成的载荷谱,即为该履带车辆中值疲劳随机载荷谱,此次试验数据就是中值载荷数据. 2.1 扭矩采集系统 扭矩采集系统的重点和难点在于如何在履带车辆上获取实时扭矩信号.履带车辆复杂的行驶工况、恶劣的试验条件会对测试系统造成很强烈的干扰.同时,履带车辆结构布局紧凑,测试关键部件处的空间狭小,给测试带来了很大不便.测试件工作温度高,震动剧烈,对传感器部件的保护工作也非常重要. 研究以装配有AMT变速装置的某轻型履带车辆为验证平台,传动系统的动力输入轴为测试点,且测试过程中不能对测试对象有任何形式的结构改变,经过对比测试采集设备及其工作原理[7-8],决定采用通过无线传输进而数据和能量传递的设备完成测试任务. 如图2所示,扭矩采集系统位于传动箱与主离合器之间,其目的是为了同时获得发动机的动态输出扭矩值与AMT变速箱的动态输入扭矩值,测试系统采用了较为先进的遥测技术,不破坏传动轴的结构,对原系统的受力几乎没有影响,可真实再现传动系统的载荷-时间历程. 图2 某型履带车辆传动机构简图 2.2 当量使用寿命及其分布 2.2.1 当量使用寿命 目前疲劳累计损伤理论主要有3种,即线性损伤累计理论、双线性疲劳累计损伤理论和非线性损伤累计理论[9-10],其中,Palmgren-Miner线性疲劳积累损伤准则应用最为广泛. 依据试验数据,每次完成特定任务工况时,发动机动力输出作用在零部件上有k级应力水平S1,S2……Sk,各级应力水平的循环数分别为n1,n2……nk.并设N1,N2……Nk分别代表在各级应力水平单独作用下的破坏循环数.D为一常量,它的取值主要取决于结构外形、材料性能和载荷形态,因为试验目的是确定最小测试次数,所以在进行对比计算时,可令D的取值为1.设T为传动轴疲劳使用寿命,根据Miner线性累积损伤理论有: (7) 已知本次试验履带车辆传动轴材料为20Cr2Ni4A,查表可知屈服极限σb(MPa)>1 483[11],在不进行构件S-N试验的情况下,为得到较为准确的寿命计算结果,可假定S-N疲劳曲线中的参数为:幂指数m=5;无限寿命幅值SE=1 000;无限寿命频次NE=107. 以每次试验工况为原始数据,利用原理公式(7)可得此典型任务工况下各次测试试验结果的当量使用寿命,如表1所示.且由公式(5)可知当量寿命T服从对数正分布,即logT服从正态分布. 表1 某典型工况的当量寿命与当量损伤 2.2.2 分布检验 根据以上的理论可知,对数当量寿命服从正态分布.为检验本次试验获得的对数当量寿命是否服从正态分布,应用概率图法,对各工况的对数当量寿命做正态分布检验,如图3所示. 从正态分布检验的概率图中可以看出,在90%的置信度下,各工况的数据点分布在拟合直线附近,且检验P值为0.268,大于0.05说明各工况的对数当量寿命都以90%的置信度符合正态分布,验证了对数当量寿命服从正态分布的理论. 图3 正态分布检验 2.3 最小测试次数确定 (8) (9) (10) 利用T分布理论(11-12),母体均值μ的区间估计式为(10). (11) (12) 查找T分布数据分布表可知,试验次数为可判断试验测试次数n是否满足给定置信度a和相对误差σ的样本量要求,式中ta为与a相对应的t分布分位数.在实际使用中,可直接查出所需的最少测试次数. 本文取置信度a=90%,相对误差限度σ=10%,可确定本次试验数据所需最小测试次数为4,实际测试次数为11次满足样本量限制,试验数据充分能够反映置信度为90%下的履带车辆传动系统受载情况,无需补充试验. 由以上分析可以确定此次典型任务工况的最小测试次数为4次,并依据试验数据编制载荷谱,以表1试验数据为基础,选取7次试验过程中的任意试验数据,进行等效损伤验证. 雨流计数法的结果与材料应力—应变迟滞环一致,故采用雨流技术法完成疲劳统计计数得到每次循环的循环次数,对每次试验数据进行汇总可得表2,采用雨流技术法完成疲劳统计计数得到每次循环的循环次数. 表2 某工况下的多次试验损伤对比 为了验证最小次数的有效性,分别以测试次数为3、4、5为数据源编制载荷谱,并由公式(7)计算对应载荷谱下产生的累计疲劳损伤,如图4至7所示. 图4 试验次数为5的疲劳损伤 图5 试验次数为4的疲劳损伤 图6 试验次数为3的疲劳损伤 图7 疲劳损伤分布图 对表中数据再进一步进行统计分析可得表3,可知不同测试次数下的疲劳损伤平均值非常接近,体现了测试试验的数据准确性. 为了衡量数据相对分散程度,将标准差除以平均值得到特征值变异系数 (11) 表3 不同试验次数的统计值与变异系数 从表3中可知,从欠试验数据的3次试验到标准试验数据的4次试验,数据方差值和变异系数都有了较大幅度的提升,数据集中度较好.说明应用该最小测试次数理论确定的最小测试次数能有效改善数据的不确定性,提高编谱数据的准确度和可靠度. 由表2分析可得本次试验次数为7次,计算所需试验次数为4,试验样本量充足,所以此7次试验数据可作为载荷谱原始数据进行编谱.由公式(5)计算可得表4.可知7次试验可靠度估计量. 表4 各组试验可靠度估计量 由中值载荷谱编制理论,可知试验5的载荷—时间历程为中值载荷谱编制数据源.对其进行雨流计数、极值推断、均幅值概率分布参数估计、联合概率密度函数、多工况合成、平均应力修正等完成载荷谱如图8和9. 图8 试验5等高线图 图9 试验5柱状图 本文成功搭建了在复杂工况下行驶的履带车辆的传动系扭矩无线测试系统,成功完成了在不改变传动轴受载的情况下的扭矩数据的动态采集工作,在具有多种典型工况的试验场获取了大量扭矩数据. 在真实数据基础上,探索履带车辆传动轴中值载荷谱编制中的原始数据样本量的确定,并对样本量计算结果进行了等效疲劳损伤验证,得出以下结论. 1)研究应用了中值载荷谱编制原理和分散系数法定寿原理,完成履带车辆当量寿命计算,运用统计图法验证其满足对数正态分布,为进一步研究履带车辆载荷谱提供了理论支撑. 2)基于典型工况的试验数据,应用正态分布母体区间估计方法,确定了该工况下的最小测试次数,避免了盲目测试,冗余数据的产生,大大降低测试成本. 3)以累计损伤为评价载荷谱数据量是否有效的依据,站在事实的角度上对最小测试次数进行验证,获得了在90%置信度以上的疲劳载荷谱. 4)运用二维谱编制方法,编制均值幅值循环次数载荷谱以及二维设计谱,为进一步研究材料结构优化理论提供了有效的数据源. [1] Heuler P, Kl Tschke H. Generation and use of standardised load spectra and load-time histories [J]. International Journal of Fatigue, 2005, 27(8): 974-990. [2] Sonsino C M. Fatigue testing under variable amplitude loading [J]. International Journal of Fatigue, 2007, 29(6): 1080-1089. [3] Morkus J. Load spectrum of a car powertrain [J]. MECCA Journal of Middle European Construction and Design of Cars, 2013, 10(3): 31-38. [4] 闫清东,张连第,赵毓芹.坦克构造与设计:(下册) [M]. 北京: 北京理工大学出版社, 2007. [5] 高镇同,熊峻江.疲劳可靠性[M]. 北京: 北京航空航天大学出版社,2000. [6] 阎楚良,高镇同. 飞机高置信度中值随机疲劳载荷谱的编制原理[J]. 航空学报,2000,21(2):118-123. [7] 党 玲, 刘云鹏, 宋美球, 等. 车辆传动装置嵌入式无线扭矩测试系统研究 [J]. 计算机测量与控制,2011,19(6):1338-1340. [8] 宋美球, 刘云鹏, 党 玲, 等. 特种车辆扭矩测试仪的研制 [J]. 车辆与动力技术, 2012(1):26-29. [9] Miner M A. Cumulative damage in fatigue[J].Journal of theApplied Mechanics,1945,67(12):159-164. [10]Manson S S.Interfaces Between Fatigue Creep and Fracture[J].Fracture:1966,2(1):51-56. [11]赵少汴, 王忠保. 抗疲劳设计—方法与数据[M]. 北京:机械工业出版社,1997. [12]Heuler P, Klätschke H. Generation and use of standardised load spectra and load-time histories[J]. International Journal of Fatigue, 2005, 27(8): 974-990. Sample Size Determination of Torque Load Testing forTracked Vehicles LIU Hai-ou1, ZHAO Zi-ye1, XU Yi2, WANG Min2, QIAO Li2 (1.School of Mechanical Engineering, Beijing Institute of Technology,Beijing 100081, China;2. China North Vehicle Research Institute,Beijing 100072, China) The compilation technique of the torque load spectrum is important for the researchon the mechanical structure design and fatigue test of the loaded parts.Taking the transmission shaft of a tracked vehicle as an example, a method for determining the sample size is proposed with a high confidence level (above 90%), based both on the compilation theory of the median stochastic fatigue load spectrum and on the principle of the equivalent life probability distribution. Through designing a system for the measurement and acquisition of the torque data,the time domain signals of the shaft are obtained under typical driving conditions. The sample size is determined and verified by the principle of the equivalent fatigue damage. The mentioned method can provide an effective original data for the load spectrum of the transmission shaft and reduce the number of test samples and test costs. tracked vehicle; the fatigue load spectrum; sample size determination; equivalent damage; high confidence level 1009-4687(2017)02-0027-06 2016-12-6 工业化和信息化部基础研究项目-车辆载荷谱编制技术研究(3030021221505) 刘海鸥(1975-), 女, 副教授, 工学博士,研究方向为车辆理论与技术及自动变速操纵控制. TU461.76 A
2 动态扭矩测试平台验证






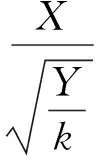
3 等效损伤验证






4 编制载荷谱

5 结 论

