基于双星编队SAR三轨法差分干涉技术的基线设计

许丽颖,王海涛

(上海卫星工程研究所,上海 201109)



基于双星编队SAR三轨法差分干涉技术的基线设计

许丽颖,王海涛

(上海卫星工程研究所,上海 201109)

将单星重复轨道三轨法差分干涉扩展到双星编队，对正侧视下合成孔径雷达差分干涉(DInSAR)技术的基线设计进行了研究。在测量坐标系中，将位于主星距离高度平面内的简化基线扩展为空间矢量，根据空间几何关系得到正侧视下双星编队SAR三轨差分干涉法的空间基线模型。建立了编队SAR测高程时基线设计公式，以及基线矢量到DInSAR测形变所需基线的转换公式，基于该模型首次从应用角度分析了基线对编队SAR三轨法差分干涉测形变的误差传播特性。给出了基于基线比的基线设计方法：测高程时，基线选择以临界基线为上限，综合考虑测高精度和灵敏度确定基线；测形变时，为降低误差对形变精度的影响，基线比应尽量小(基线比为0.25时编队SAR三轨法DInSAR形变测量精度最高)，即地形图像对的垂直有效基线应尽量大，形变图像对的基线应尽量小。用ALOS-2卫星参数进行了仿真计算，所得编队基线和重复轨道基线误差要求分别为毫米级和厘米级。研究对DInSAR系统中基线参数设计有更直观的理论指导意义和实际应用价值。

双星编队； 合成孔径雷达差分干涉； 三轨法差分干涉； 高程； 形变； 基线； 误差传播； 形变精度

0 引言

DInSAR技术具有覆盖范围大、空间分辨率高、成本低、能监测识别潜在地表形变的优势，非常适合我国自然和气候环境复杂、幅员辽阔、形变观测技术条件和能力有限的情况，在地质灾害、土地资源、地壳变形、基础测绘、防灾减灾等领域有广阔的应用前景[1-4]。地表形变前后的两幅SAR图像的干涉相位信息既包含地形信息又包含形变信息。DInSAR原理是采用一定方法获取地形相位并将其从形变相位中去除，得到地表形变信息。根据地形信息相位的获取方式，DInSAR可分为二轨法、三轨法和四轨法，其中三轨法选取形变前或形变后两幅图像干涉得到地形相位图，避免了使用外部DEM数据，配准难度亦小，目前应用较广。

当前差分干涉形变测量试验都基于重复轨道卫星观测实现，差分精度受基线误差、大气效应和时间去相干等因素的影响很大[5-7]。将传统单星重复轨道三轨法推广，通过利用双星编队SAR获得地形相位信息可提高形变测量精度[8]。因双星编队SAR在获取地形相位的同时可获得图像对，不存在时间去相干，受大气效应影响小，并能利用星间测量设备获得高精度星间基线等，但其系统设计和处理方法等的研究相对滞后，开展基于双星编队SAR系统的差分干涉研究有其现实意义[9]。干涉相位误差与基线误差是影响视线向形变检测精度的主要因素。基线是差分干涉SAR工作原理中的关键系统参数，既是基线去相干的根源，又反映地形干涉相位图的质量，且影响测高灵敏度。系统设计时，合理选择基线长度和给出基线测量精度需求尤为重要。目前已开展的编队SAR差分干涉研究多基于基线在主图像距离高度平面内的简化模型，获得满足简化模型条件的干涉图像对较难，实际处理过程中图像对的几何关系复杂，尤其是对编队SAR系统，当基线不在主图像距离高度平面内时，干涉关系存在一定的特殊性，基线不再是标量而是一个空间矢量[10-11]。基于空间基线模型进行编队SAR差分干涉系统研究是进行后续研究的基础，但目前对基于差分形变应用的基线误差设计需求的研究较少。本文对正侧视条件下双星编队SAR三轨差分干涉法进行了研究，分析形变测量和基线的传递链路，给出了基于基线比的基线设计方法，基于编队SAR差分干涉三轨法的空间几何模型，讨论了编队SAR双星测高程的基线选择，从编队测高需求与形变测量精度需求分析了基线长度和测量误差对视线向形变检测精度的影响，给出了传播模型。

1 空间几何关系

双星编队SAR三轨法测地表形变的方法利用双星编队SAR一次航过获得形变前主辅图像slcl，slc2，进行干涉得到地形相位信息，利用重复轨道卫星得到形变后的第三幅图像slc3，与主图像干涉得到形变相位信息。空间几何关系如图1所示。图1中：点O为地心；T为形变前目标点的位置；D为形变后位置；h为形变矢量；S1为编队航过主星成像中心时刻的位置；S2为辅星位置；S3为卫星重复航过成像中心时刻的位置；r1，r2，r3分别为主星、辅星和重复航过卫星的视线矢量；I为卫星S-1所成图像的距离高度平面；II1为S1，S2，O确定的平面，双星编队的地形基线B12在平面II1内；II2为S1，S3，O确定的平面，重复轨道的形变基线B13在平面II2内；III为卫星S-1的轨道面；θ为主星的下视角；β2，β3分别为基线B12，B13的方位角；Φ2，Φ3分别为基线B12，B13的高度角。

图1 三轨法差分干涉SAR空间几何关系Fig.1 Spatial geometry of three-track DInSAR

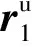
B12=

B12[cosφ2cosβ2cosφ2sinβ2-sinφ2]T

(1)

(2)

(3)

将基线B12分解为三个分量：视线向水平基线B12∥、距离向垂直有效基线B12⊥和方位向垂直有效基线B12a，分别为

sinφ2cosθ)

(4)

sinφ2sinθ)

(5)

B12a=B12cosφ2cosβ2

(6)

其中：B12∥，B12⊥都位于距离高度平面I内，是干涉与差分干涉的有效基线；B12a垂直于距离高度平面I，是动目标检测(GMTI)的有效基线。

2 基于星载双星编队SAR三轨法差分干涉技术的基线选择

2.1 编队SAR测高程基线选择

对编队干涉SAR系统，有效干涉基线为垂直视线方向的干涉基线分量，空间基线引起的干涉回波信号间的频谱偏移不能大于雷达信号带宽，否则无法进行干涉测量，因此需根据系统参数计算一个临界基线B⊥c，有

(7)

式中：BW为信号带宽；τy为地形坡度角；λ为波长；R0为中心斜距；θ0为中心视角；c为光速[11]。忽略地球曲率的影响，相位估计精度与测高精度的传递函数为

(8)

(9)

地形高度主要与相位估计精度σφ和h2π有关，而基线与两者都相关，基线越长高程灵敏度越高，基线通过相关系数影响相位估计精度。σφ与干涉图像的相关系数满足关系

(10)

式中：NL为视数；γ为分布式星载SAR干涉去相关系数，可表示为噪声去相关、几何去相关、体散射去相关等因素的乘积。忽略体散射影响，基线长度能引起的去相关因素为几何去相关

(11)

式中：ρr为距离向分辨率。由式(10)、(11)可知：基线越短越好。

总体上，基线选择以临界基线为上限，使测高精度最高，即高程误差最小的基线是获取DEM的有效基线；增加基线长度可提高测高灵敏度，但会增加几何去相关，降低相位估计精度，选择基线时需考虑这两者因素。

2.2 三轨法测形变基线选择

2.2.1 基本原理

slcl，slc2包含地形信息。忽略大气相位误差和扰动误差，rti，rri分别表示发射星和接收星与地面散射单元距离，双星编队SAR一发双收模式下rt1=rr1=r1,rt2=r1,rr2=r2。根据几何关系r2=r1-B12，可得地形图像对干涉相位

(12)

在星载SAR系统中，存在关系r1≫B12，将φ12作泰勒展开，仅保留1/r1的一阶项，则有

(13)

slcl，slc3的图像对包含形变信息，在重复轨道时，两次航过获得的形变图像对存在一定时间和空间基线，将造成大气相位延时、地物去相关等，进而引起干涉相位噪声。忽略相位噪声，同理在rt1=rr1=r1rt3=rr3=r3,r3=r1+h-B13几何关系下，干涉相位

(14)

同样存在关系r1≫B13,B13≫h，将φ13作泰勒展开，仅保留1/r1的一阶项，可得由地形相位φtopo和形变相位φdefo组成的相位

(15)

式中：hr为沿航迹方向的视线向变量。

在差分干涉处理中，真正需要反演的变量是形变信息，用式(13)从干涉相位φ13中去除编队飞行获得的地形相位，所算得的剩余形变相位φdefo可用于反演形变信息。由去平地效应法可得

(16)

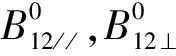
2.2.2 基线选择

基线和干涉相位是影响形变测量精度的重要因素。三轨法差分干涉有两条基线，两幅干涉相位图会引入误差，求视线向形变hr的偏导可得相位误差和基线误差传播系数，进而得到基线范围和测量精度需求。对式(16)求偏导可得相位误差传递公式为

(17)

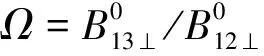
(18)

可知：当基线比为0.25时，误差传递系数最小，可获得的形变精度更好，如前文所述地形图像对有效基线会增加几何去相关，选取有效基线需同时考虑这两个因素。

由于干涉测高、地形变化都对星间基线误差非常敏感，本文基于形变测量精度给出了基于编队SAR三轨法差分干涉对基线测量误差的传递函数

(19)

式中：σB12y,σB13y分别为基线B12，B13在y轴向的误差；σB12z,σB13z分别为基线B12，B13在z轴向的误差。当雷达正侧视时，沿航迹方向的基线误差不会影响最终的形变检测精度，由误差传播系数计算公式(19)可知：为降低误差对形变精度的影响，基线比应尽量小，地形图像对的垂直有效基线应尽量大，形变图像对的基线应尽量小。地形图像对是由双星编队SAR一次航过得到，基线会受编队构形的限制，也将受几何去相干的限制。

3 仿真分析

参考ALOS-2卫星选择系统参数给出基线设计结果，卫星参数为：轨道高度628 km；下视角31°；频率，L波段1.25 GHz；分辨率3 m；方位模糊比(AASR)-18 dB，距离模糊比(RASR)-20 dB。入射角在范围20°～53°内，仿真计算所得不同视角的临界基线长度如图2所示。

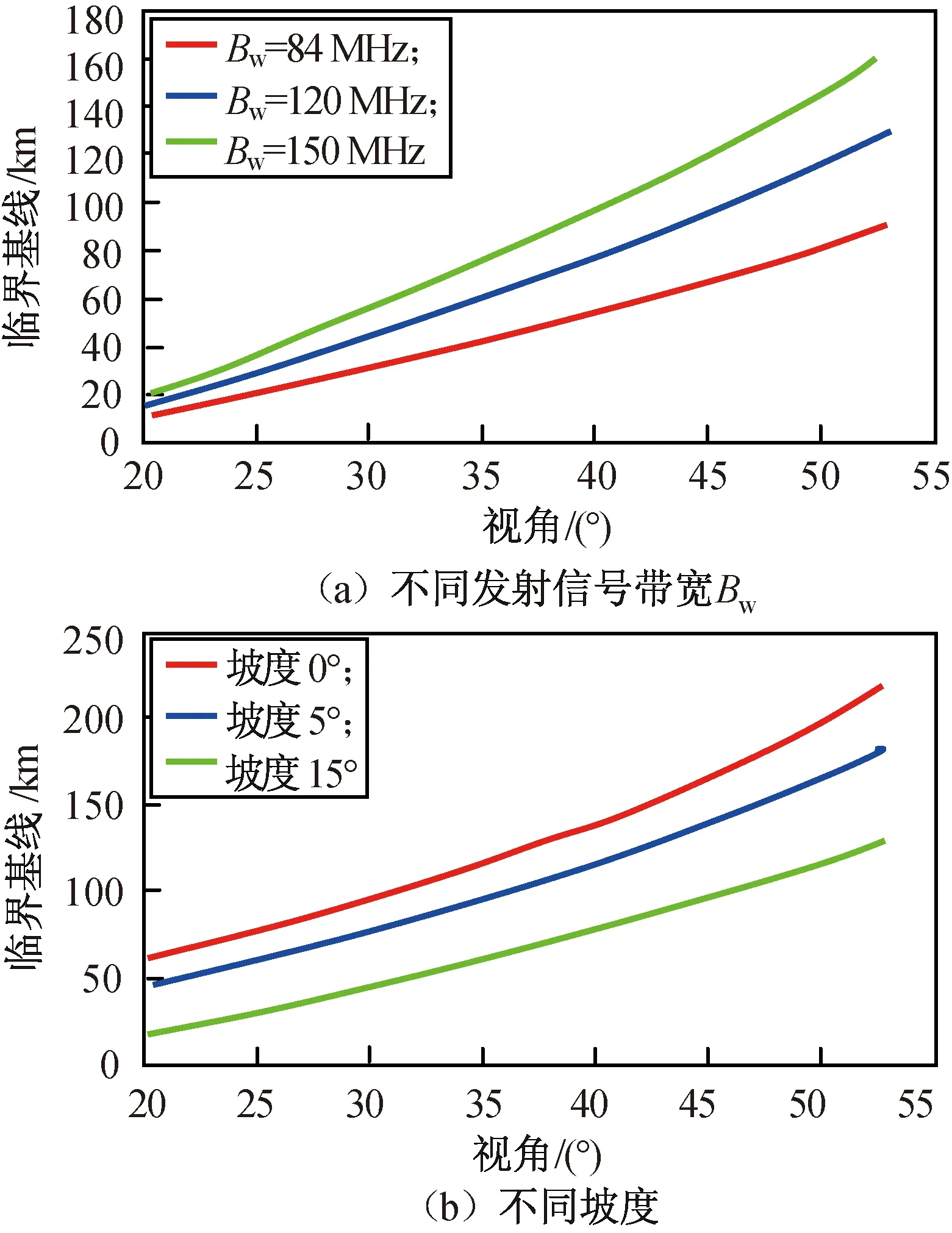
图2 不同条件下不同视角的临界基线长度Fig.2 Critical baseline length under various incidence angles

由图2可知：临界基线长度随视角增大而增加，不同带宽和坡度时临界基线值不同，带宽越宽临界基线越长，地形坡度越大临界基线就越短。当带宽为84 MHz时，平地测绘对应的临界基线为55～210 km，山地测绘对应的临界基线为10～120 km。

在干涉测高时，不同的基线长度条件下干涉相位条纹变化反映了不同的高程变化，使测高精度最高也就是高程误差最小的基线是获取DEM的有效基线。在相同系统参数条件下，仿真所得不同基线时平地和山地区域的相对测高精度如图3所示。

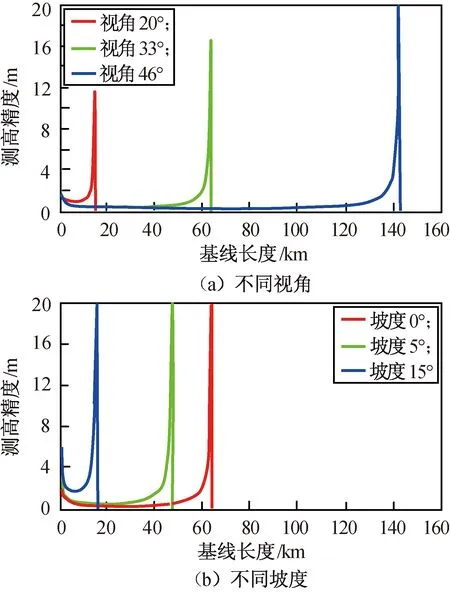
图3 不同基线的测高精度Fig.3 Relative height accuracy as a function of baseline

由图3(a)可知：基线长度受高度敏感度和几何去相关两个因素影响，需在一定范围内取值，视角越小基线范围越窄。图3(b)为视角条件最差的情况，可发现平地时为满足测高精度2 m的要求，基线长度应取0.75～61.5 km，高山区域时为满足测高精度5 m的要求，基线长度应取0.5～13.25 km。基线长度越长相位解缠的难度越大，选择基线时需综合考虑。

如前文所述，相位误差对三轨法形变测量影响的大小受基线比的制约，在满足地形测绘精度的条件下，需合理选择形变基线长度，以满足形变精度需求，根据本文参数选择地形基线长度0.5～13.25 km，仿真所得不同基线比的形变精度如图4所示。

图4 不同基线比的形变精度Fig.4 Deformation accuracy under various baselines

由图4可知：当基线比为0.25时精度最好；随着基线比的增大，编队SAR三轨法D-InSAR形变测量精度变差。但实际情况中很难准确地选择基线比为某个确定值，此外基线越长相位解缠越困难，对形变图像对来说时间去相关越严重，选择形变基线时需综合考虑。形变图像对的获得时间间隔也将影响相干性，它必须与观测目标相匹配，如对海洋观测，因表面变化非常快，时间基线必须是秒或毫秒量级，但对地壳变形等缓慢形变过程的应用，则时间基线为数年才能进行精确测量。

当基线长度确定后，需进一步分析对编队SAR三轨法差分干涉仿真试验中的误差传播系数，得到对基线测量精度的需求。用典型值后的形变误差计算结果见表1。

表1 典型误差值的形变精度计算结果

Tab.1 Deformation accuracy under typical error conditions

误差源σϕ12σB12yσB12zσϕ13σB13yσB13z典型值10°2mm2mm10°10cm5cm视线向形变误差1 6mm1×10-6mm1×10-6mm3 2mm25 8mm23 57mm

由表1可知：双星编队SAR三轨法差分干涉处理中，干涉相位误差引起的形变误差较小，可保持在毫米量级。形变检测误差主要源于形变图像对的基线误差，且主要是切航迹向及垂直向的基线误差，需要高精度的星间基线以大幅提高形变检测精度。

4 结束语

本文在空间基线的基础上结合雷达差分干涉测量的原理，将单星重复轨道三轨法差分干涉推广到双星编队。基于空间基线，由形变测量精度给出了用基线比设计给出误差需求的设计方法，对DInSAR系统设计有重要的参考价值。建立了编队SAR差分干涉三轨法的空间几何模型，并给出了基线矢量到DInSAR测形变所需基线的转换公式；分析了干涉测高和三轨法差分干涉测形变的相位，给出了基线的选择方法和基线误差对形变检测精度的影响；推导了基线比对三轨法形变测量的影响，当基线比为0.25时星载编队SAR三轨法DInSAR形变测量精度最高。与传统依据重复轨道形变图像对相干性选择基线的方法相比，本文方法更符合DInSAR形变测量的应用需求，更直观可靠。因实践中很难固定某个基线比，后续将进一步研究不同地物时间去相干的影响。总体来讲，需选择尽可能较小有效基线的形变干涉对和较大有效基线的地形干涉对进行差分干涉处理，另外形变图像对切航迹向以及垂直向的基线误差是形变测量误差的主要来源。本文研究对DInSAR系统中基线参数设计有更直观的理论指导意义和实际应用价值。

[1] PEPE A, EUILLADES L D, MANUNTA M, et al. New advances of the extended minimum cost flow phase unwrapping algorithm for SBAS-DInSAR analysis at full spatial resolution[J]. IEEE Tansactions on Geoscience and Remote Sensing, 2011, 49(10): 4062-4079.

[2] HU Zhe, GE Lin-lin, LI Xiao-jing, et al. An underground-mining detection system based on DInSAR[J]. IEEE Tansactions on Geoscience and Remote Sensing, 2013, 51(1): 615-625.

[3] ALIMUDDIN I, BAYUAJI L, TETUKO S S J, et al. Surface deformation monitoring of Miyakejima volcano using DInSAR technique of ALOS PALSAR images[C]// In Proc IEEE IGARSS, 2011. Vancouver: IEEE, 2011: 1615-1618.

[4] CHANG H, GE L, WANG H, et al. Radar interferometry for 3-D mining deformation monitoring[C]// In Proc IEEE IGARSS 2007. Barcelona: IEEE, 2007: 2090-2092.

[5] RAUCOULES D, MICHELE M D. Assessing ionospheric influence on L-band SAR data: implications on coseismic displacement measurements of the 2008 Sichuan Earthquake[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(2): 286-290.

[6] BOMBRUN L, GAY M, TROUVE E, et al. DEM error retrieval by analyzing time series of differential interferograms[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(4): 830-834.

[7] NOLAN M, FATLAND D, HINZMAN L. DInSAR measurement of soil moisture[J]. IEEE Trans on Geoscience and Remote Sensing, 2003, 41(12): 2802-2814.

[8] KRIEGER G, FIEDLER H, HAJNASEK I, et al. TanDEM-X: mission concept and performance analysis[C]// In Proc IEEE IGARSS, 2007. Barcelona: IEEE 2007: 4890-4893.

[9] ZHANG K, NG A-M, LI X, et al. A new approach to improve the accuracy of baseline estimation for spaceborne radar interferometry[C]// In Proc IEEE IGARSS, 2009. Cape Town: IEEE, 2009: 162-165.

[10] 何峰, 梁甸农, 刘建平. 星载双基地SAR干涉测高误差分析[J]. 系统工程与电子技术, 2005, 27 (9): 1519-1521.

[11] FABIO G, ANDREA M G, FRANCESCO P, et al. The wavenumber shift in SAR interferometry[J]. IEEE Trans on Geoscience and Remote Sensing, 1994, 32(4): 855-865.

Baseline Design of Three-Track Formation Based on Spaceborne SAR Differential Interferometry

XU Li-ying, WANG Hai-tao

(Shanghai Institute of Satellite Engineering, Shanghai 201109, China)

The baseline design of differential synthetic aperture radar interferometry (DInSAR) was studied for side looking while the three-track method for single satellite was extended to bi-satellite formation in this paper. Through extending the simplified baseline scalar in height-range plane to spatial vector, the spatial baseline model of three-track side looking DInSAR was obtained according to the spatial geometry in measurement coordinate system. The equation of baseline design was established for detecting elevation of formation SAR. And the transfer equation of baseline from baseline vector to DInSAR deformation measurement was also given. On the basis of this model, for the first time the error transfer characteristics from DInSAR deformation accuracy was analyzed at the point of view of application. The baseline design method based on baseline ratio was put forward. The upper limitation of baseline was the critical baseline for elevation detection. The baseline shall be selected for considering elevation detection accuracy and sensitivity. And the baseline ratio shall be as small as possible to reduce the influence of error on the accuracy for deformation detection. The vertical effective baseline of terrain image pair shall be as long as possible and the baseline of deformation image pair shall be as small as possible. The accuracy of deformation detection for three-track formation of DInSAR was the best when the baseline ratio was 0.25. The simulation computation was carried out by using ALOS-2 satellite parameters. The results showed that the baseline requirements of formation and repeat orbit were millimeter and centimeter respectively. The study has more clearly theoretical meaning and application value for designing baseline of DInSAR system.

bi-satellite formation; differential synthetic aperture radar interferometry (DInSAR); three-track differential interferometry; elevation; deformation; baseline; error transfer; deformation accuracy

1006-1630(2017)03-0060-06

2016-08-06；

2016-11-09

国家自然科学基金资助(41501414)

许丽颖(1987—)，女，博士，主要从事合成孔径雷达载荷总体设计。

TN958

A

10.19328/j.cnki.1006-1630.2017.03.008