空间非合作目标近程自主跟踪的全局鲁棒最优滑模控制研究

王洪宇,杨雪勤,贡 鑫

(上海宇航系统工程研究所,上海 201109)



空间非合作目标近程自主跟踪的全局鲁棒最优滑模控制研究

王洪宇,杨雪勤,贡 鑫

(上海宇航系统工程研究所,上海 201109)

对空间非合作目标的近程自主跟踪过程中目标可能会由于不确定原因出现轨道变动时的近程自主跟踪控制问题进行了研究，提出了一种全局鲁棒最优滑模控制器方法。针对空间非合作目标自主跟踪问题的标称系统，由基于无限时域的二次型性能指标的最优控制理论，获得最优调节器，再构造一个积分滑模面，使系统开始即在滑模面上，消除了传统滑动模态中的趋近模态，并使控制系统滑动模态与对应标称系统的最优动态有相同的形式，则滑动模态亦是渐近稳定的，且具有完全的鲁棒性；为保证滑动模态的存在，设计了滑模变结构控制器。该方法吸取了最优控制和滑模控制的优点，可在优化燃耗的同时满足全局鲁棒稳定性。仿真分析结果表明：用该法可实现对空间非合作目标轨道变动时的自主稳定跟踪，保证跟踪的精度。

空间非合作目标； 轨道变动； 近程； 自主跟踪； 相对动力学模型； 最优滑模控制； 全局鲁棒

0 引言

空间非合作目标包括故障或失效卫星、空间垃圾、未知航天器等。对空间非合作机动目标实现长期、自主、精确的跟踪，能有效用于在轨服务、卫星编队等多项空间技术领域中，并利于空间操作和空间任务的完成。对空间非合作目标近程自主跟踪控制问题来说，非合作目标可能进行主动的轨道变动，由于无法获得其加速度，因此会产生一些不确定因素。目标航天器的变动引起目标轨道不确定变化，两航天器间相对位置的变化规律也将随之发生改变，这种改变使目标随着时间的推移，可能会飞出追踪航天器自主跟踪能力定义的界限，并最终因跟踪机制的缺陷而导致失跟。为避免该情况发生，延长对非合作性机动目标的跟踪时限，需考虑追踪航天器的自主机动控制，以用基本方法解决轨道变动目标的自主跟踪问题。

随着编队飞行等其他空间任务的广泛开展，对航天器闭环控制的需求有拓展，基于应用背景对各种闭环控制问题进行了充分研究。文献[1]将在轨服务系统对非合作目标的最优机动控制问题描述为一个标准线性规划问题，通过线性规划优化方法，对在轨服务系统的接近路径进行优化并能确定相应的燃耗，对相对运动的一种特例目标悬停进行控制器设计，实现了近距离目标悬停相对轨道的精确控制，为在轨服务系统的工程实现提供了技术支持。文献[2]提出了直接以发动机产生向心力对目标进行绕飞的控制方法，并完全利用跟踪航天器上光学相机提供的观测信息，设计了一种在绕飞面控制视线转率为非零常值，同时在纵平面辅以比例导引的制导方法，使跟踪航天器能在以目标为中心的近圆相对轨道上飞行。文献[3]根据CW方程设计了初制导律，在视线坐标系中建立了微型航天器与非合作目标间的相对运动方程，并设计了空间交会自寻的末制导律。交会任务开始时，为节省微型航天器的燃料，轨道平台根据初制导律以一定速度及释放角度释放微型航天器，微型航天器进入交会轨道，在初制导的作用下，经过若干个过渡轨道周期后接近空间非合作目标，并为末制导提供良好的交班条件，当末制导导引设备捕获并跟踪目标后可通过自寻的末制导最终完成与空间非合作目标交会任务。实际上，非合作目标自主跟踪控制就是利用相对运动状态跟踪结果的反馈进行的闭环控制。空间环境中的追踪航天器能力有限，设计闭环自主控制律时，除满足基本的稳定控制指标外，燃耗是最重要的考虑因素。与此同时，系统内外部扰动的普遍存在则对平台自主控制的鲁棒性提出了要求。由于鲁棒性的取得一般来自最优性的牺牲，鲁棒与燃耗优化指标间存在矛盾，因此兼顾系统的鲁棒性与燃耗的最优性是非合作目标跟踪控制问题的核心[4]。

对航天器的闭环控制，应用较广的是最优控制，但无法满足非合作目标不确定性轨道变动的跟踪问题。针对非合作目标自主跟踪问题鲁棒性的控制需求，应用较多的H∞鲁棒控制，未考虑燃耗的优化问题[5]。针对非合作目标的近程自主跟踪控制问题，本文采用的全局鲁棒最优滑模控制，可兼顾考虑系统的鲁棒性和燃耗的优化问题，使系统在解决非合作目标自主跟踪问题的前提下同时满足燃耗的需求。针对非合作目标自主跟踪问题的标称系统，由基于无限时域的二次型性能指标的最优控制理论，获得最优调节器，再构造一个积分滑模面，使系统开始即在滑模面上，消除了传统滑动模态中的趋近模态，并使控制系统滑动模态与对应标称系统的最优动态有相同的形式，则滑动模态亦是渐近稳定的，且具有完全的鲁棒性；为保证滑动模态的存在，设计了滑模变结构控制器。通过仿真验证了设计方法对非合作目标自主跟踪问题的有效性。

1 非合作目标跟踪问题动力学模型

空间非合作目标自主跟踪控制主要研究两近距离航天器间的轨道运动，建立两航天器间的相对动力学模型是实施有效控制的基础[6-7]。

空间两飞行器相对几何关系如图1所示。在惯性参考系中，非合作目标轨道动力学方程可表示为

(1)

追踪器轨道动力学方程可表示为

(2)

非合作目标与追踪器的位置可表示为

(3)

(4)

图1 空间两飞行器相对几何关系Fig.1 Relative geometry between two spacecrafts

式(2)减去式(1)，并将式(3)、(4)代入，可得

dS-dT

(5)

dS-dT

(6)

在目标轨道系中，两飞行器相距仅数十千米，可简化摄动影响，对两器间的引力差进行线性化简化处理，将相对轨道动力学方程写成状态空间形式。定义状态向量为

(7)

将相对轨道动力学方程写成状态空间形式

(8)

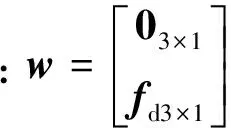
(9)

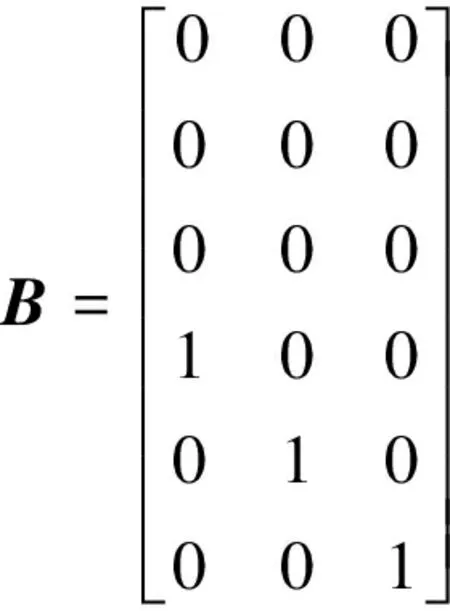
(10)

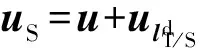
2 最优滑模控制设计

滑模变结构控制理论是通过控制作用强迫从任意点出发的状态轨迹到达某滑模面，然后沿此滑模面滑动至平衡点[8-10]。这种控制策略与常规控制的根本区别是控制的不连续性，即系统“结构”随时变化，迫使系统沿规定的状态轨迹作小幅度、高频率的振动，这种运动称之为滑动模态或“滑模”运动。滑动模态是可设计的，且与系统的参数及扰动无关，这导致滑模变结构控制具快速响应、对参数变化及扰动不灵敏、无需系统在线辨识、物理实现简单等优点。随着滑模变结构控制理论的发展，其适用的系统与控制任务己越来越广，涉及到确定与不确定系统、同步系统与时滞系统、连续与离散系统、线性与非线性系统、集中参数与分布参数系统、随机系统、大系统等。最优滑模控制将积分滑模控制与最优控制结合，使控制器既具鲁棒性，又有最优性[11]。

2.1 最优滑模控制系统

对非合作目标的自主跟踪问题的动力学模型，因非合作目标可能存在未知机动，考虑系统式(8)的不确定性，有

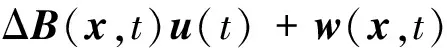
(11)

式中：ΔA(x,t)，ΔB(x,t)为未知的时变函数矩阵，分别对应A，B的不确定部分。

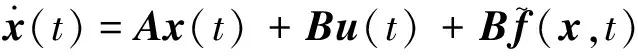
(12)

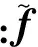
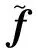
(13)

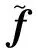
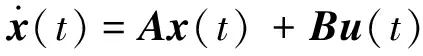
(14)

对非合作目标自主跟踪控制，针对系统的不确定性，选择控制律为

(15)

式中：ul为线性部分的连续控制律，为理想控制，用以稳定和优化标称系统式(14)；ubl为不连续控制项，用以补偿系统式(11)中的不确定因素的影响。

2.2 标称系统的最优控制

针对标称系统式(15)，根据最优控制理论，存在唯一的最优控制律u*(t)，使性能指标

(16)

为最小。此处：Q∈Rn×n为半正定的状态加权矩阵；R∈Rm×m为正定的控制加权矩阵。

标称系统使性能指标取最小值的最优状态反馈控制律为

(17)

式中：P∈Rn×n为正定常数对称阵，为代数Riccati方程

(18)

的唯一解。将该最优控制律作为式(14)中的连续部分，即ul=u*(t)，将其代入系统式(15)，则闭环系统的最优动态方程为

(19)

根据最优控制理论，闭环系统是渐近稳定的。但若将该控制律直接用于有不确定性的系统，而不设计不连续控制部分，则系统的状态轨迹将会偏离系统的最优轨线，甚至不稳定。

2.3 全局鲁棒最优滑模面

基于积分滑模原理进行全局鲁棒最优滑模面的设计，一方面使系统一开始就运动在切换流形上，取消传统滑模变结构控制中的趋近状态，保证系统的整个动态过程具不变性；另一方面使理想滑模态的状态轨迹与标称系统的最优轨线一致。

对不确定性系统式(12)，构造积分滑模面

s(t)=G[x(t)-x(0)]-

(20)

式中：G∈Rm×n为滑模面系数矩阵且满足GB是非奇异的；x(0)为系统的初始状态(已知)。对任意状态的x(0)，积分滑模面式(20)都有s(0)=0，从而取消了趋近模态。

G(A-BR-1BTP)x=GΔAx+G(B+

ΔB)u+Gw+GBR-1BTPx=0

(21)

则将系统式(12)的等效控制

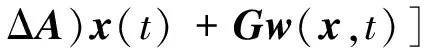
(22)

代入系统方程，得系统的理想滑动模态方程

[G(BR-1BTP+ΔA)x+Gδ]+w=

(A+ΔA)x-(B+ΔB)[G(B+ΔB)]-1×

[GΔAx+Gδ+GBR-1BTPx]+w=

(A-BR-1BTP)x

(23)

比较式(19)、(23)可知：不确定系统的理想滑模动态方程与标称系统的最优动态方程完全一致。

因不确定系统的理想积分滑模运动轨迹与标称系统的最优轨线完全相同，故称式(20)为全局鲁棒最优滑模面，式(23)为最优滑动模态，且最优滑动模态对满足匹配条件的参数的不确定性和外界扰动，具完全的鲁棒性。

2.4 全局鲁棒最优滑模控制律

对非合作目标自主跟踪控制问题，按式(20)构造的积分公式选取滑模面，滑模控制律u=ul+ubl保证起始于状态空间任意位置的状态轨迹都能在有限时间内到达滑模面且随后一直保持在其上。此处有

(24)

(25)

式中：sgns=[sgns1sgns2… sgnsm]T；η为适当的正的常数。

2.5 滑模稳定性

取Lyapunov函数V=(1/2)sTs，则

sT{G[(A+ΔA)x+(B+ΔB)u+w]-

G(A-BR-1BTP)x}=

sT{(GB)[-R-1BTPx-(GB)-1(η+

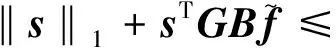
-η‖s‖1-η0‖GB‖‖s‖1+

η0‖GB‖‖s‖≤-η‖s‖1<0

(26)

式(26)表明：所选取的滑模控制律，滑模存在条件和有限时间到达条件成立，说明不确定系统起始于任意点的状态在形如u=ucon+udis的控制律的作用下均能在有限时间内到达滑模面，并随后一直保持在其上，则系统的整个动态过程对给出的二次型性能指标以及满足匹配条件的不确定性是全局鲁棒最优的。

3 仿真与分析

假设追踪航天器初始时刻位于目标飞行器后方23 km、下方11 km处，追踪航天器自主进行近程跟踪逼近，最终两航天器理想相对运动状态为[0 0 0 0 0]。目标从时间1 000 s开始持续机动，在沿目标航天器轨道坐标系x、y轴各施加加速度0.03 m/s2。仿真时间6 500 s，仿真周期0.1 s。优化性能指标

式中：

Q1=[100 0 0 0 0 0]

Q2=[0 100 0 0 0 0]

Q3=[0 0 100 0 0 0]

追踪航天器与目标航天器的初始轨道参数见表1。分别用最优控制、H∞控制和最优滑模三种控制方法进行仿真。所得最优控制的相对位置与速度的仿真结果分别如图2、3所示，H∞控制所得相对位置与速度的仿真结果分别如图4、5所示，最优滑模控制所得相对位置与速度的仿真结果分别如图6、7所示。

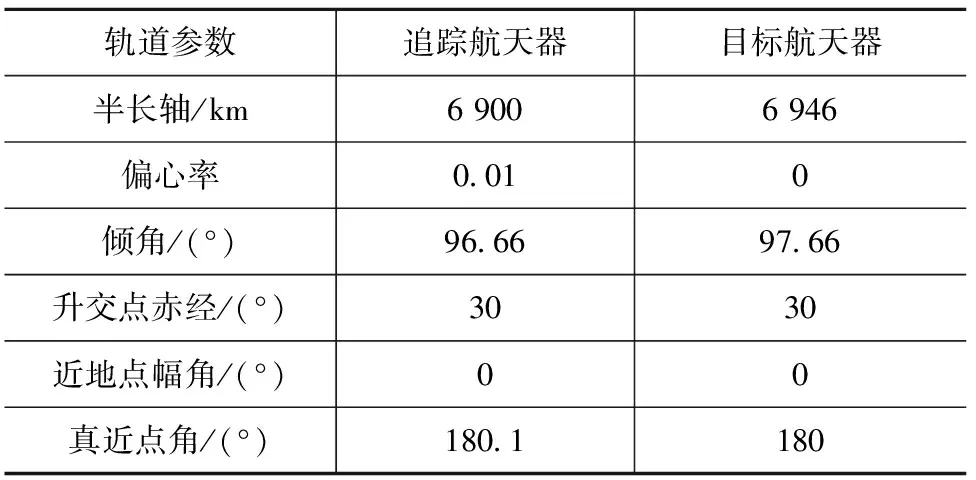
表1 初始轨道参数

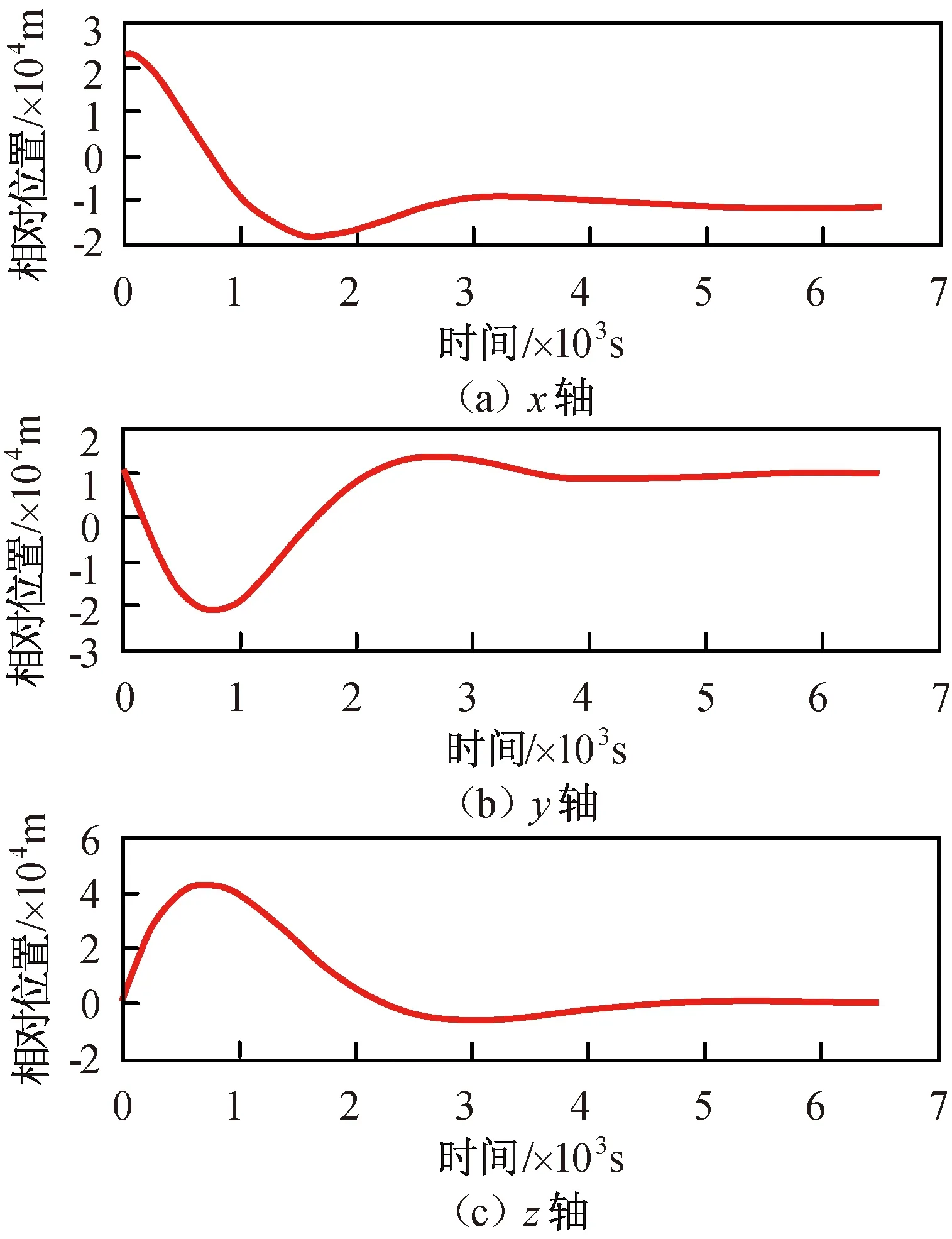
图2 最优控制相对位置变化Fig.2 Relative position changes under optimum control

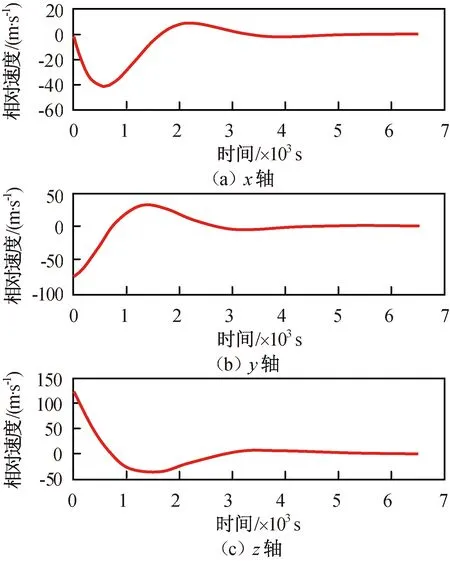
图3 最优控制相对速度变化Fig.3 Relative velocity changes under optimum control

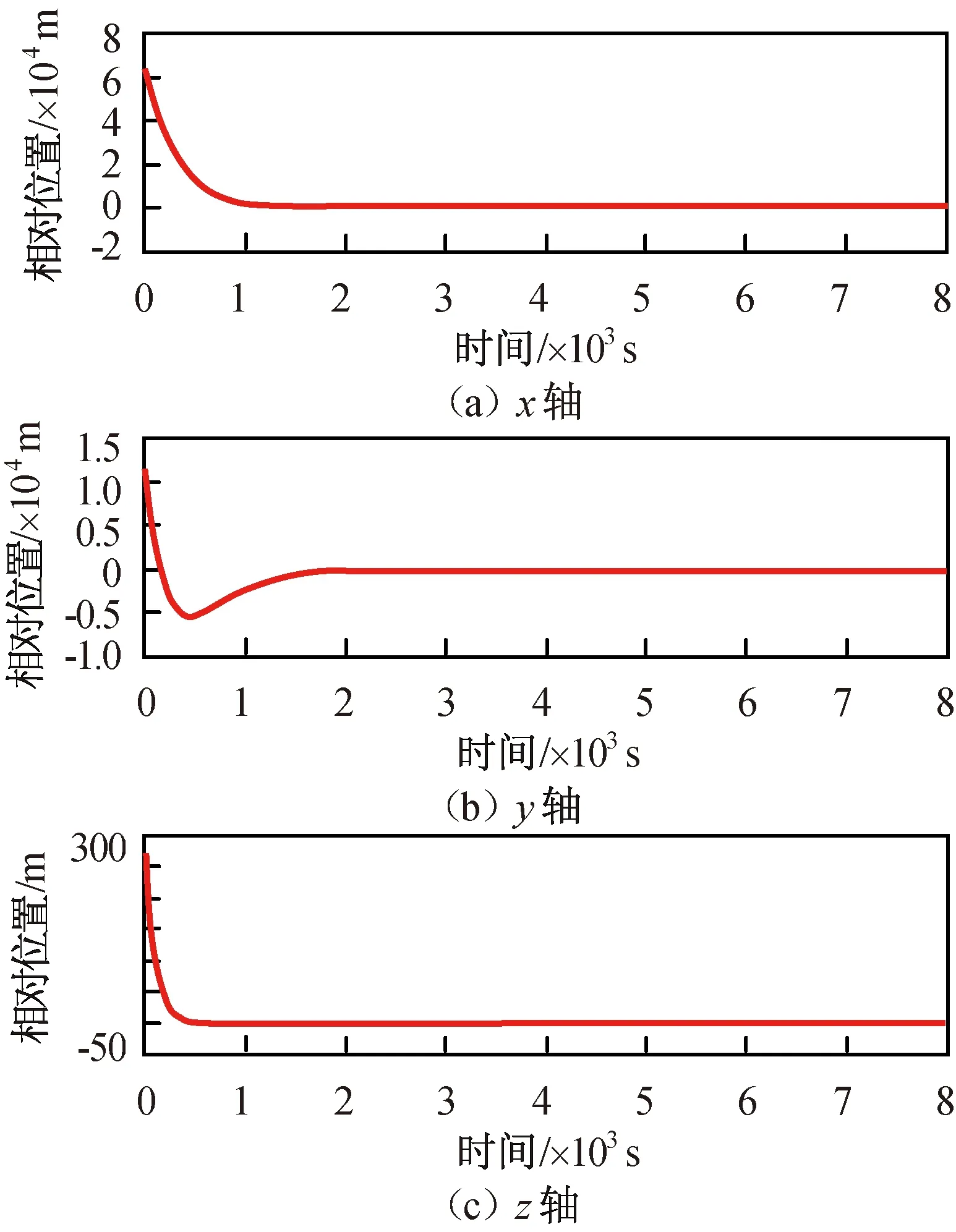
图4 鲁棒H∞控制相对位置变化Fig.4 Relative position changes under H∞ robust control

图5 鲁棒H∞控制相对速度变化Fig.5 Relative velocity changes under H∞ robust control

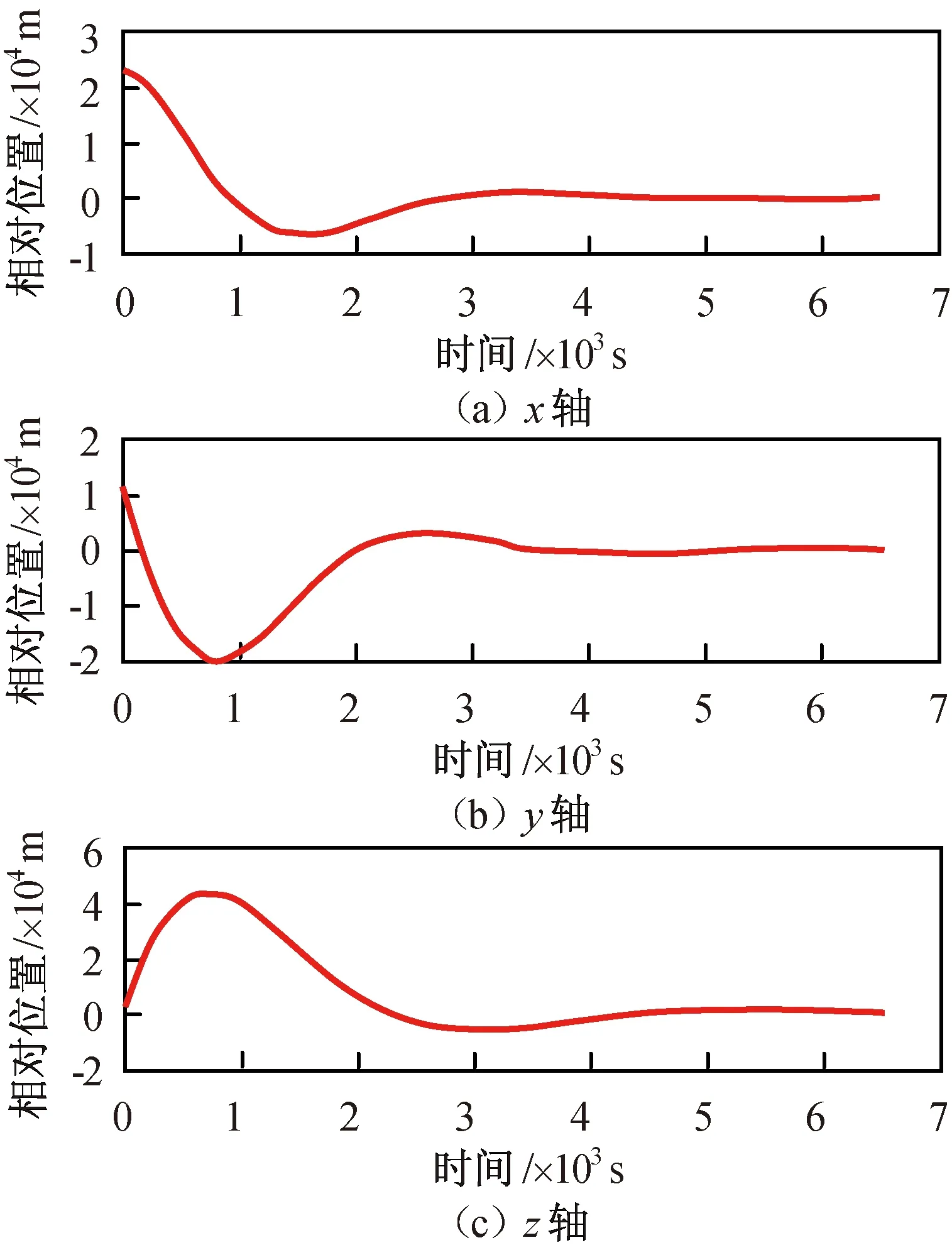
图6 最优滑模控制相对位置变化Fig.6 Relative position changes under optimal sliding-mode control

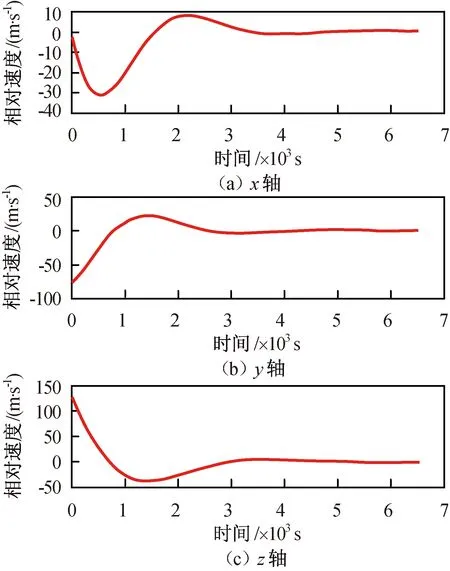
图7 最优滑模控制相对速度变化Fig.7 Relative velocity changes under optimal sliding-mode control

因最优控制方法在目标机动的情况下系统发散，故只比较了H∞控制与最优滑模控制方法机动过程中的速度增量，结果见表2。

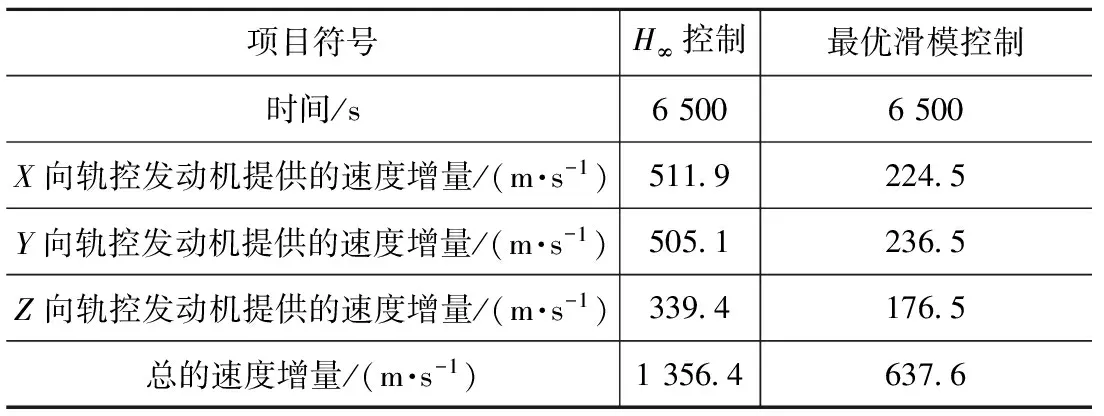
表2 不同控制方法机动过程中的速度增量

由仿真结果可知：

a)最优控制方法虽可用于优化燃耗，但在非合作目标存在轨道变动时系统出现发散，无法完成对非合作目标的稳定控制；H∞控制和最优滑模控制可满足非合作目标自主跟踪的鲁棒性要求。

b)最优滑模控制相对位置、相对速度曲线均收敛，系统达到平衡状态，且所需的速度总增量637.6 m/s，远小于H∞控制，说明最优滑模控制能在目标存在机动的情况下实现对目标的有效跟踪控制，动态响应几乎不受扰动或目标机动的影响，且兼顾燃耗的优化。

综合仿真结果可知：本文设计的方案可行，能在保证系统燃耗优化的同时，对外界扰动等不确定性有较强的鲁棒性。

4 结束语

本文针对非合作目标的近程自主跟踪控制问题进行了研究。用全局鲁棒最优滑模控制器的设计方法，构造了一种积分滑模面，使系统一开始就在滑模面上，消除了传统滑动模态中的趋近模态，并使控制系统滑动模态与对应标称系统的最优动态有相同的形式，保证系统的整个动态过程具鲁棒性和燃耗的优化性。对最优控制、H∞控制、最优滑模控制三种方法进行了仿真以验证本文方法的有效性，结果表明：在目标轨道变动情况下，全局鲁棒最优滑模控制表现出较好的鲁棒性，且相对其他控制方法，在保证鲁棒性的前提下兼顾考虑燃耗优化。

[1] 苏晏, 李克行, 黎康. 非合作目标追踪与相对状态保持控制技术研究[J]. 空间控制技术与应用, 2010, 36(6): 51-55.

[2] 兰宏炜, 江涌. 目标监视绕飞导引方法研究[J]. 系统工程与电子技术, 2008, 30(9): 1735-1739.

[3] 崔乃刚, 张立佳. 微型航天器与空间非合作目标交会制导方法[J]. 航空学报, 2009, 30(8): 1466-1471.

[4] 李元凯. 空间救援目标自主随动跟踪与控制研究[D]. 上海: 上海交通大学, 2010.

[5] ZHENG Q, WU F. NonlinearH∞control designs with axisymmetric spacecraft control[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(3): 850-859.

[6] 杨雪勤, 王洪宇, 冯刚. 失效卫星救援过程中相对导航研究[J]. 上海航天, 2015, 32(4): 1-7.

[7] 邢光谦, 冯刚, 张宝恒. 一种追踪航天器近程逼近目标及保持伴飞的实现方法: ZL200910125447[P]. 2009-10-12.

[8] 高为炳. 变结构控制的理论和设计方法[M]. 北京: 科学出版社, 1998.

[9] UTKIN V I. Variable structure system with sliding modes[J]. IEEE Transactions on Automatic Control, 1977, 22(2): 212-222.

[10] UTKIN V, SHI J. Integral sliding mode in systems operating under uncertainty conditions[C]// In Proc Conference on Decision and Control. Kobe: [s. n.], 1996: 4591-4596.

[11] 逄海萍. 一类不确定仿射非线性系统的最优滑模控制[D]. 青岛: 青岛科技大学, 2010.

Study on Global Robust Optimal Sliding-Model Control for Space Non-Cooperative Target of Short Range Auto Follow-Up Problem

WANG Hong-yu, YANG Xue-qin, GONG Xin

(Aerospace System Engineering Shanghai, Shanghai 201109, China)

The short range autonomous tracking and control of space non-cooperative target was studied when the target might maneuver uncertainly because of unknown reasons in the follow up. The global robust optimal sliding-model control algorithm was put forward in this paper. For the nominal system of the tracking problem of the space non-cooperative target, the optimal controller was obtained by optimal control theory based on infinite-time quadratic performance index. The integral sliding-model was constructed to make the system on the sliding surface at first, which eliminated the approach module in traditional sliding-model. And this would make that the sliding-model of the control system had the same form with relative nominal system. So the sliding-model would be asymptotic stability and have totally robustness. The variable structure controller was designed to ensure the existence of sliding-model. This control algorithm combined the advantages of both optimal control and sliding-mode control and achieved global robustness and the optimizing fuel consumption at the same time. The simulation results showed that this controller would be used in non-cooperative target autonomous tracking problem, and it could guarantee the tracking precision.

space non-cooperative target; orbit maneuver; short range; autonomous tracking; relative dynamic model; optimal sliding-model control; global robust

1006-1630(2017)03-0088-07

2016-08-19；

2016-09-16

王洪宇(1989—)，男，硕士，主要从事飞行器总体设计。

V448

A

10.19328/j.cnki.1006-1630.2017.03.012