基于星间测距增强的卫星编队GPS相对导航研究
张 伟,杜耀珂,李东俊,王 瞧,金小军,徐兆斌,金仲和
(1.浙江大学 微小卫星研究中心,浙江 杭州 310027; 2.上海航天控制技术研究所,上海 201109; 3.航天恒星科技有限公司,北京100086)
基于星间测距增强的卫星编队GPS相对导航研究
张 伟1,杜耀珂2,李东俊3,王 瞧1,金小军1,徐兆斌1,金仲和1
(1.浙江大学 微小卫星研究中心,浙江 杭州 310027; 2.上海航天控制技术研究所,上海 201109; 3.航天恒星科技有限公司,北京100086)
针对单纯差分GPS系统在精度、连续性、实时性方面存在的问题,提出了一种星间测距增强差分GPS的卫星编队组合相对导航方案。该组合相对导航系统由编队卫星中分别安装的GPS接收机、星间RF测量传感器,以及主星中运行的导航处理器组成,其中星间RF测量传感器集成了窄带通信功能,可在进行星间距离测量的同时同步进行GPS数据的互传。采用扩展Kalman滤波算法,结合简化动力学模型和GPS以及RF测量数据实现卫星编队的相对位置与速度的高精度实时递推解算。用模拟器采集数据进行了仿真验证,结果表明:在星间测距数据辅助下,星间基线长度在星间测距工作的30 km范围内时,实时相对导航精度优于1 mm;系统在GPS信号中断时仍可连续输出满足精度要求的相对位置、速度数据;系统初始化时间由单纯差分GPS相对导航系统的几十个历元降低到单点。
卫星编队; 相对导航; 组合导航; 伪距; 载波相位; 差分GPS; 星间测距; 扩展Kalman滤波
0 引言
微小卫星编队卫星间的相对导航是编队协同工作的基础,相对导航精度决定了编队能达到的应用水平。基于差分GPS的相对导航系统是目前卫星编队导航的主要手段,有代表性的应用有: 2002年发射的GRACE双星编队,地面事后处理的星间基线确定精度达到毫米级;2010年发射的PRISMA双星编队,GPS实时相对导航精度达到厘米级,事后处理可达到亚厘米级;2014年发射的加拿大CanX-4/CanX-5双星编队由两颗仅重6.85 kg的纳卫星组成,GPS相对导航精度优于10 cm[1-5]。但单纯基于差分GPS(CDGPS)的编队导航技术存在一些突出的问题。一是连续导航能力受限:编队卫星由于共视GPS卫星不足、编队任务中实施机动等因素造成无法获取足够多的GPS观测量,而仅依靠轨道动力学模型进行推算,1 min后误差就已较明显[6]。文献[4]中的分析表明低轨双星编队仅有70%~80%的时间能获得足够多的GPS观测量。二是导航精度受限:地面事后处理已达到毫米级的精度极限,而实时导航精度一般只能达到厘米级[7]。三是导航实时性受限:编队初始化或观测数据中断再恢复后的重新初始化过程常需要数十个历元[3,8]。
在编队中增加星间自主射频(RF)测量传感器获取星间测距数据,从而形成增强导航系统或组合相对导航系统,是克服单纯基于差分GPS编队导航系统缺陷的有效途径。由于星间RF测量在编队内完成,信号连续性易保证,将星间RF测量与GPS测量结合,可明显提升连续导航能力和系统鲁棒性;另外卫星编队的星间距离相对较短(一般为数米至数百公里),星间RF测量能获得较GPS信号更优的信噪比条件,因此两种测量的组合可突破纯GPS导航系统的精度极限;由于星间RF测量精度较高,可明显提升组合导航系统收敛的速度,导航实时性可得到有效提高。在国外,星间RF测量技术得到了一定的发展,其中有代表性的是:PRISMA编队的飞行射频(FFRF)传感器,星间测距精度1 cm,视角测量精度1°;GRACE/GRAIL编队的K波段测距(KBR)系统,星间测量精度达到了微米级[1-3]。但对PRISMA卫星编队的星间RF测量系统来说,其相对导航应用还存在的问题有,一是厘米级的RF测量精度还不能满足一般编队应用的需求,另一是仅基于星间RF测量的编队导航系统不能自主运行,需要地面或星载GPS接收机提供绝对轨道信息。KBR系统的问题则是,其本质上是一种距离变化的测量方法,依赖于地面事后处理,系统自主性和实时性受限,同时系统过于复杂,难以在微小卫星上应用。本文以航天器编队应用为背景,针对现有单纯基于GPS、GPS增强或组合导航方法在导航连续性、相对导航精度、导航实时性等方面的不足,提出了一种基于高精度星间测距数据增强差分GPS的卫星编队组合相对导航方案,在分析组合相对导航系统结构的基础上,提出了GPS和星间测距的伪距和载波相位观测模型,给出用扩展卡尔曼滤波(EKF)方法解算卫星编队相对位置与速度的组合相对导航估计算法,最后对所提方法的导航精度、连续性和实时性进行仿真验证。
1 组合相对导航系统
基于差分GPS/星间测距的组合相对导航系统由GPS接收机、星间RF测量传感器、导航处理器及相应接口组成,其系统结构如图1所示。GPS接收机由主星(A)GPS接收机和从星(B)GPS接收机组成,主星GPS接收机将接收的GPS星历和观测数据同时发送给组合相对导航处理器和GPS实时定轨子处理器,而从星GPS接收机直接将获得的GPS星历和观测数据通过RF测量传感器的通信通道发送给组合相对导航处理器。GPS实时定轨子处理器通过EKF滤波器解算出主星位置rA、速度vA并传送给组合相对导航EKF滤波器用于时间更新解算。星间RF测量数据输入主星星间测距解算子处理器解算出高精度的基线长度数据rAB,用于组合相对导航EKF滤波器观测更新。组合相对导航处理器接收GPS实时定轨模块、星间测距解算模块和GPS接收机模块发送的相关数据,用EKF滤波器解算出卫星编队的相对位置和速度。

图1 组合相对导航系统结构Fig.1 Architecture of integrated relative navigation system
不同于PRISMA/FFRF,GRACE/KBR等自主测量系统,本文所用星间RF测量采用复合伪码测距结合双程转发载波测距方法,能以较简单的传感器结构获得较高的测量精度(理论上能达到微米级的测距精度)。同时,将交换GPS,RF测量数据的窄带通信功能集成到RF传感器的测量通道,由于采用双程测量方式,能易实现编队节点间的信息互传。在基于GPS的编队导航系统中,则需专门建立通信链路完成测量数据的交换。
因此,采用GPS,RF测量耦合构成组合导航系统,一方面可利用高精度的RF测量数据,突破单纯基于GPS的编队导航的精度极限;另一方面星间RF测量中复合伪码为载波测量解整周模糊,能实现单点实时测量,因此RF测量与GPS耦合有助于加快相对导航系统初始化过程,而这对导航实时性要求较高的编队任务是非常有用的。
2 组合相对导航估计算法
两颗低轨微小卫星以主从星模式构成双星编队,其每颗卫星均安装有双频GPS接收机和RF测量传感器,以获取伪码和载波相位观测量。
组合导航估计算法用EKF滤波的方法递推解算出编队的相对位置和速度[9-10]。其中:在EKF的时间更新中,以实时定轨模块获取的主星A的位置和速度为参考点,结合四阶龙格-库塔方法和简化动力学模型递推出从星B的位置与星间基线矢量;在测量更新中,以GPS双差观测量和星间测距解算获得的星间测距观测量构成测量更新观测矢量,实现星间测距与GPS的耦合。
2.1 观测模型
2.1.1 GPS观测模型
卫星双频GPS接收机工作于GPS L1、L2C频点,由于双星编队星间距离小于30 km,在大部分时间内,两个GPS接收机能共视足够数量的GPS导航星,用双差的方法消除观测量中的共有误差项实现编队卫星高精度相对定位。
a)GPS伪距观测量
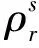
(1)
式中:c为光速。
b)GPS载波相位观测量
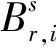
(2)
c)差分GPS观测量
由a)、b)伪距和载波相位观测量可构成GPS无差(UD)观测量zUD(t),有
(3)
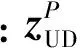
GPS无差(UD)观测量zUD(t)可由转换矩阵DU,S转换成GPS单差(SD)观测量zSD(t),有
(4)
式中:
(5)
GPS单差(SD)观测量zSD(t)通过转换矩阵DS,D转换成GPS双差(DD)观测量zDD(t),有
(6)
式中:
(7)
2.1.2 星间测距观测模型
星间测距系统(ISRS)采用有别于GPS的测距体制,由复合伪码测距方法结合双程转发载波测距方法组成。
a)ISRS伪距观测量
伪距观测方程为
(8)
式中:ρ(t)为真实距离;ρT(t)为双程测量时相对运动导致瞬时距离值误差;IP为电离层折射引起的误差;MP为多径引起的误差;εP为随机噪声及测量方法引入的误差。
b)ISRS载波相位观测量
双程转发载波测距星间距离测量值可表示为
(9)

c)RF星间测距解算
ISRS星间测距解算采用Kalman滤波方法,解算模块输入量为伪距观测量和载波相位观测量,输出量为星间距离值。
Kalman滤波器状态量可表示为
(10)
式中:ρ为星间距离值;N为载波对应整周模糊度。
Kalman滤波器观测模型采用a)、b)中所述伪距和观测模型,观测向量可表示为
(11)
式中:ρp为伪距观测量;C为载波相位观测量。
系统观测矩阵可表示为
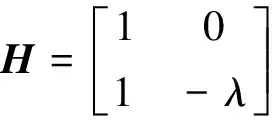
(12)
2.2 组合相对导航估计算法
设组合相对导航EKF滤波器状态量为
(13)
式中:rAB,vAB分别为ECI坐标系中六维星间基线位置和速度矢量;IAB为GPS单差(SD)电离层路径延迟,为n=32维矢量,分别对应32颗GPS卫星;BAB为GPS单差载波相位模糊度值,为2n=64维矢量,分别对应L1、L2频点处的32颗GPS卫星。此处:
(14)
在某一历元,当卫星不可见时,则将该颗卫星对应的电离层路径延迟IAB和模糊度BAB清零;当某颗GPS卫星重新可见时,则将对该颗卫星对应的IAB,BAB赋初值。即
(15)
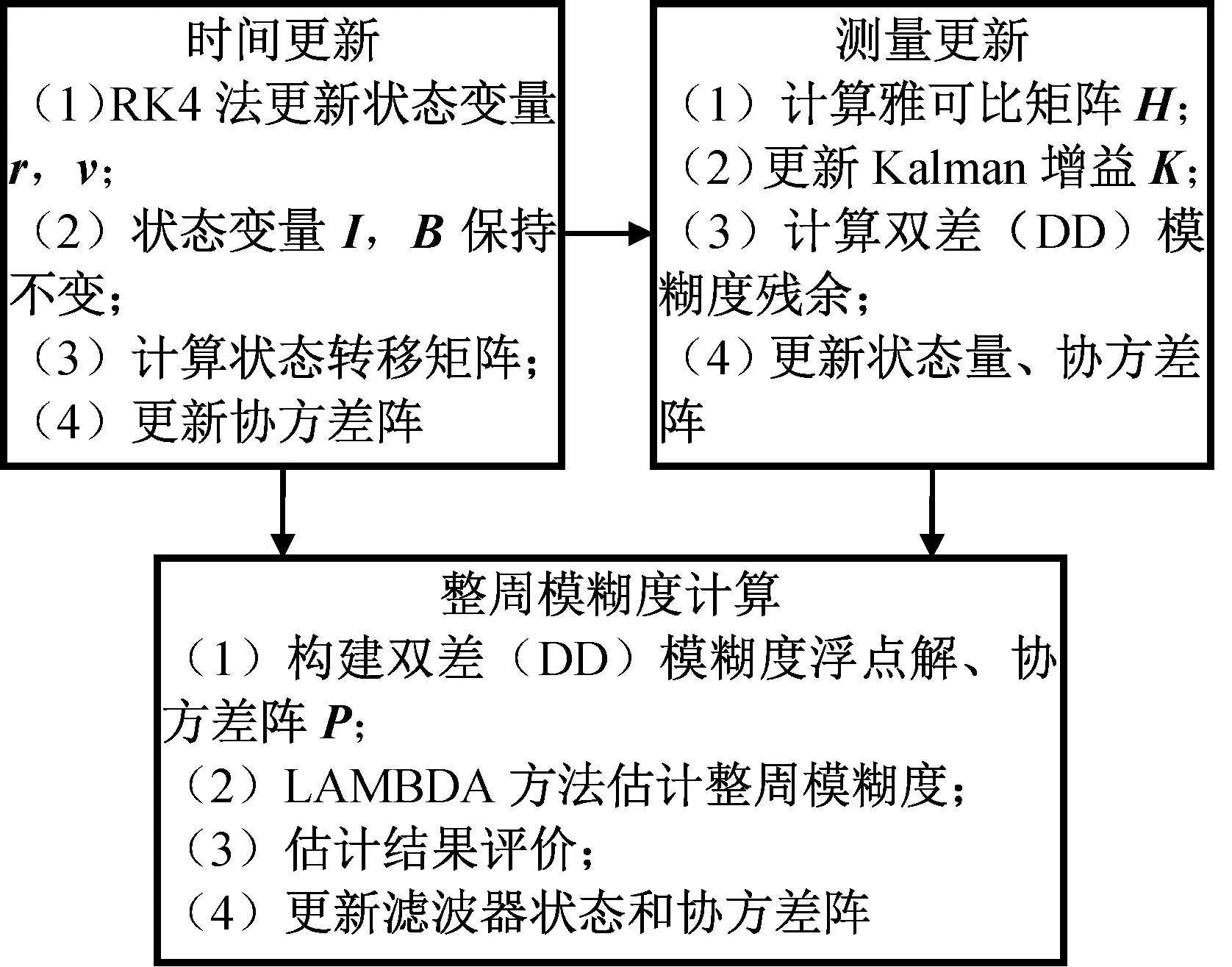
图2 组合相对导航EKF滤波器更新流程Fig.2 Update scheme of EKF filter for integrated relative navigation system
测量更新中,观测矢量由GPS双差(DD)观测量zi, GPS和星间测距观测量zi, ISRS组成,zi, GPS可通过转换矩阵DU, S,DS, D从无差(UD)观测量转换得到,星间测距观测量由ISR观测模型对原始星间测距观测数据处理后得到。有
(16)
雅可比矩阵为
(17)
式中:h为状态量和观测矢量间关系的非线性函数;E为惯性系中主星指向从星的视线单位矢量;f1,f2和λ1,λ2分别为GPS L1,L2频点频率和波长。
3 系统验证方法及结果
本文根据GPS模拟器产生所需数据,用MTLAB/C平台仿真方法进行性能验证。GPS模拟器采用思博伦GNSS信号模拟器GSS9000,通过分时工作的方式产生A、B两星的GPS广播数据和卫星轨道数据。两颗卫星运行于高度约530 km近圆轨道,A星轨道参数为半长轴6 907 395.5 m,倾角97.430 4°,升交点赤经-64.438 9°,偏心率0.001 163,平近点角75.753 2°,近地点幅角128.103 8°;B星轨道参数除真近点角外与A星相同,通过控制两颗卫星真近点角之差可获得不同星间距离的仿真场景。
对A、B两颗卫星的轨道数据作差即可得真实星间距离数据,作为对比基准用于组合相对导航系统性能验证。
星间测距数据由A、B两星真实星间距离数据再加噪声得到。根据星间链路预算,星间基线长度小于等于30 km时,星间测距解算模块能正常通信以传送GPS测量数据。同时,为使星间测距获得优于毫米级的测距精度,要求星间测距伪码测量精度优于1个载波波长(约13 cm)。伪码测量精度与接收信号强度的关系如图3所示。其中:当星间基线长度为30 km时,接收信号强度约-101.5 dBm,伪码测量精度约11 cm,满足要求。因此,模拟器仿真中,取A、B星星间距离为30 km。值得一提的是,星间测距解算模块历元间隔为1 s,其滤波器收敛时间远小于组合导航滤波器历元间隔30 s,因此星间测距解算模块输出数据不会对组合导航滤波器的实时性产生影响。
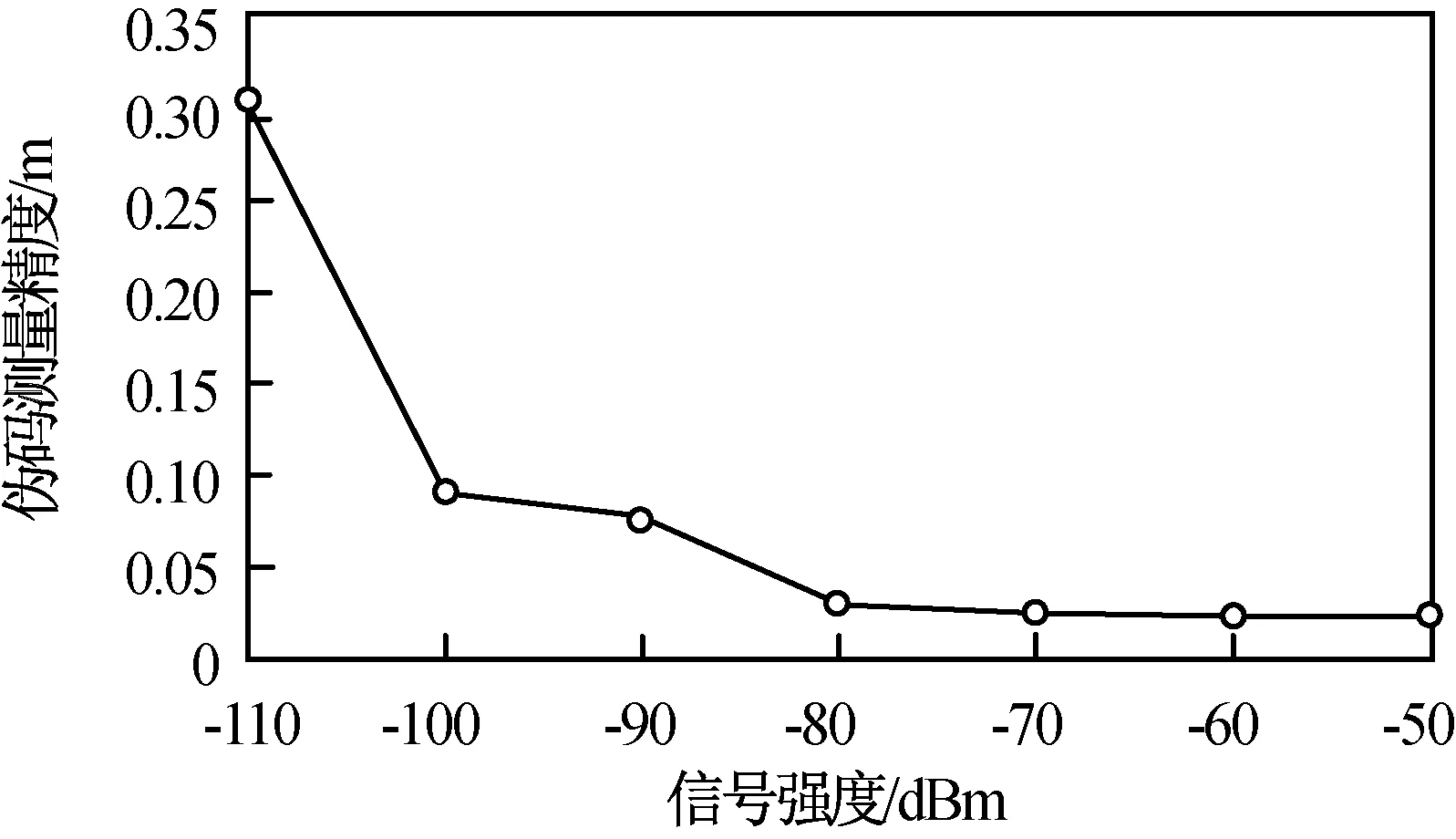
图3 星间测距伪码测量精度Fig.3 Pseudo code ranging error in inter-satellite ranging system
经测试,星间基线长度为30 km时,星间测距3D 均方差(RMS)精度优于0.5 mm。因此在真实相对距离基准值中添加RMS值约0.5 mm的高斯白噪声构成星间测距数据,其中高斯白噪声用于模拟星间测距数据中的相对距离误差。
3.1 实时相对导航精度
在基线长度约30 km条件下进行仿真,仿真时长24 h,仅用差分GPS观测数据所得相对距离的误差如图4所示。其中:3D RMS精度为0.028 7 m。

图4 差分GPS相对导航系统相对距离误差Fig.4 Relative range error of carrier differential GPS relative navigation system
附加RMS精度为0.5 mm的星间测距数据后,由组合相对导航系统所得相对距离误差如图5所示。其中:3D RMS精度为0.546 mm。由此可知:星间测距数据能显著提高相对导航系统的3D RMS精度。
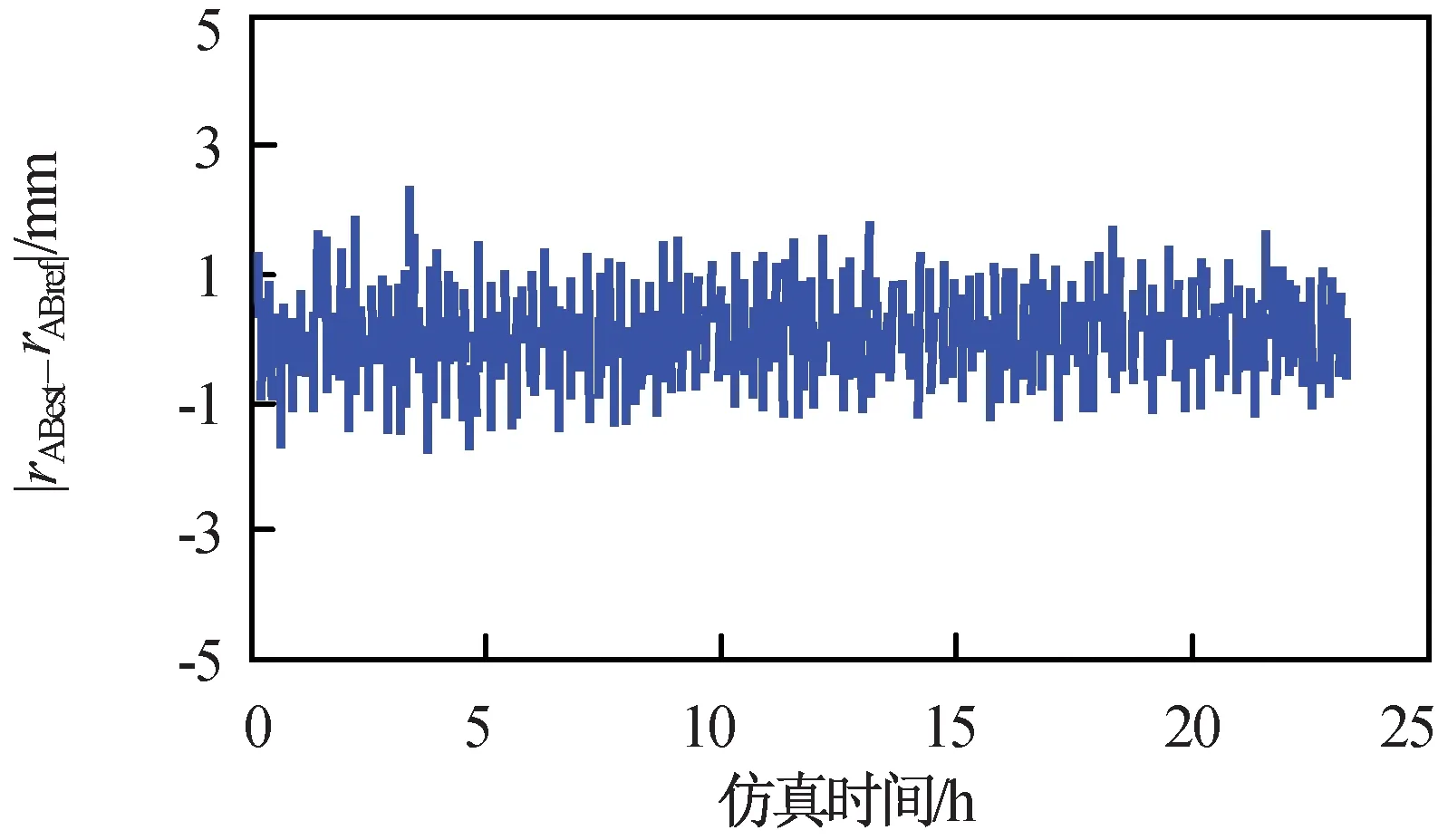
图5 星间测距辅助差分GPS相对导航系统相对距离误差Fig.5 Relative range error of inter-satellite ranging augmented system
3.2 导航连续性
在差分GPS相对导航系统中,在GPS观测数据出现中断时,由动力学模型进行相对位置与速度的更新和传递,但当GPS观测数据中断时间过长时,动力学模型解算值精度将无法满足需求[相对距离误差|Δr|<3σ(此处:σ为正常解算误差3D RMS值)],导致导航系统输出值中断[10]。用基线长度30 km的差分GPS观测数据,仿真时长5 h,所得观测数据在仿真时间2~3 h的区间内中断,如图6(a)所示。图中:红线之间为3σ区间。由图6(a)可知:观测数据中断20 min后,相对距离误差达到3σ(0.09 m),而在1 h的中断区间内,相对距离误差最大可达0.17 m,中断区间内RMS值为0.130 6 m。因此,根据仿真结果,当GPS观测数据中断约20 min,差分GPS相对导航系统即无法输出满足精度要求(相对距离误差小于0.09 m)的相对位置、速度数据。在GPS观测数据中断处引入RMS精度为0.5 mm的星间测距数据辅助后,所得观测数据如图6(b)、(c)所示。由图6(b)、(c)可知:中断处相对距离误差均小于2 mm,中断处RMS值为0.56 mm。因此,根据仿真结果,在星间测距辅助下,GPS观测数据中断时相对导航系统仍可输出满足精度要求的相对位置与速度数据。
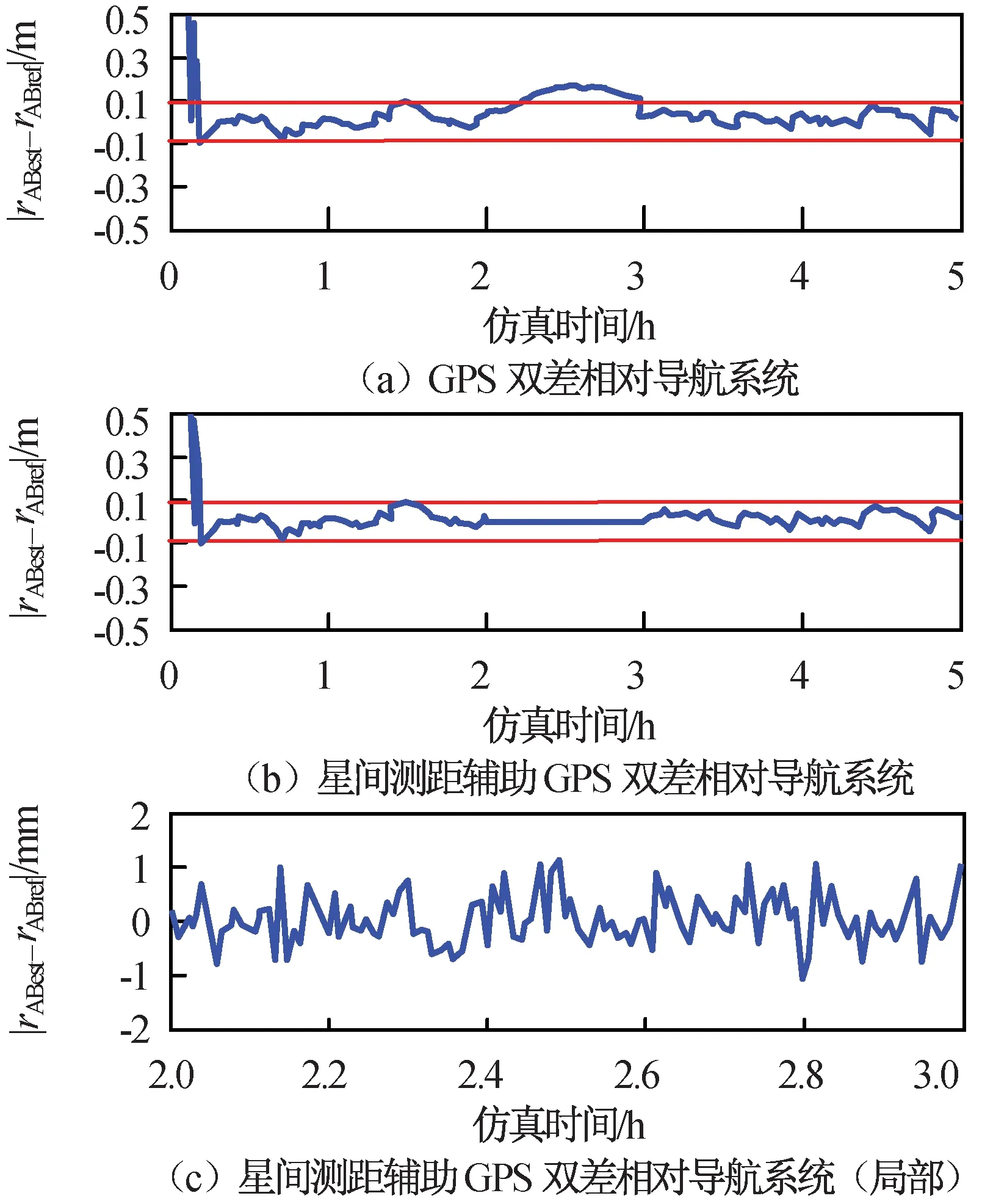
图6 GPS观测数据中断和星间测距辅助相对导航误差Fig.6 Relative navigation errorfor pure CDGPS and inter-satellite ranging augmented system during a GPS data interrupt
3.3 导航实时性
差分GPS相对导航系统和星间测距辅助差分GPS相对导航系统的初始化局部如图7所示。由图7(a)可知:差分GPS相对导航系统需24个历元收敛至其3D RMS值的3σ区间内。由图7(b)可知:在前5个(小于24)历元中加入RMS精度为0.5 mm的星间测距数据构成星间测距辅助差分GPS相对导航系统后,系统初始化时间显著减少,1个历元即可收敛,在星间测距辅助的前5个历元内其3D RMS精度为0.001 1 m,在5个历元后,无星间测距数据辅助下,3D RMS精度为0.028 7 m,恢复到差分GPS相对导航系统精度水平。
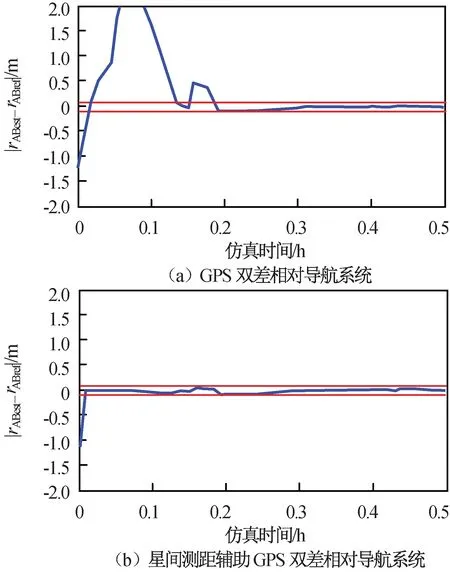
图7 差分GPS相对导航系统和星间测距辅助差分GPS相对导航系统初始化结果Fig.7 System initialization for pure CDGPS and inter-satellite ranging augmented system
上述仿真结果表明:在星间测距数据辅助GPS差分相对导航系统初始化下,相对导航系统实时性达到单点。
4 结束语
本文给出了一种星间测距增强差分GPS的卫星编队组合相对导航方案。在编队中增加星间自主射频(RF)测量传感器获取星间测距数据,同时结合GPS双差模型形成增强导航系统,能克服单纯差分GPS编队导航系统在导航实时性、连续性和导航精度上的缺陷,同时也可解决星间测距系统只能提供星间距离而无法提供星间矢量的问题。本文分析了组合相对导航系统结构和算法,并进行了仿真验证。仿真结果表明:在星间测距数据辅助下,星间基线长度在星间测距工作的30 km范围内时,实时相对导航精度优于1 mm;系统在GPS信号中断时仍可连续输出满足要求的相对位置与速度数据;系统初始化时间由GPS差分相对导航系统的数十个历元降低到单点。
本文从理论上验证了算法的可行性,后续可从以下对算法进行改进:一是数据来源,使用实验室研制的高动态GPS接收机接收模拟器信号产生真实GPS测量数据,同时星间测距数据由编队真实距离加从星间测距传感器获取的噪声获得;二是改进星间测距传感器,提高其可用星间距离,扩展系统使用范围;三是分析天线相位中心、天线分布对组合导航系统的影响;四是随着北斗全球导航系统的组网完成,可采用多GNSS导航系统以改善导航星的几何构型,在提高系统的定轨精度的同时增强系统的可靠性。
[1] KROES R, MONTENBRUCK O, BERTIGER W, et al. Precise GRACE baseline determination using GPS[J]. GPS Solutions, 2005(9): 21-31.
[2] DELONG N. PRISMA relative orbit determination using GPS measurements: 21st International Symposium on Space Flight Dynamics[C]// Toulouse: 2009.
[3] D’AMICO S, ARDAENS J-S, MONTENBRUCK O. Navigation of formation flying spacecraft using GPS: the PRISMA Technology Demonstration, ION-GNSS-2009[C]// Savannah: 2009.
[4] EYER J K. A dynamics and control algorithm for low earth orbit precision formation flying satellites[D]. Toronto: University of Toronto, 2009.
[5] ROTH N H. Navigation and control design for the CanX-4/-5 satellite formation flying mission[D]. Toronto: University of Toronto, 2010.
[6] MONTENBRUCK O, GILL E. State interpolation for on-board navigation systems[J]. Aerospace Science and Technology, 2001, 5(3): 209-220.
[7] D’AMICO S, MONTENBRUCK O. Differential GPS: an enabling technology for formation flying satellites: Small Satellite Missions for Earth Observation-New Developments and Trends[C]// Berlin: 2010.
[8] LEUNG S, MONTENBRUCK O. Real-time navigation of formation-flying spacecraft using global-positioning-system measurements[J]. Journal of Guidance, Control, and Dynamics, 2005, 28: 226-235.
[9] KROES R. Precise relative positioning of formation flying spacecraft using GPS[M]. Rotterdam: Optima Grafische Communicatie, 2006.
[10] 王甫红. 高精度星载GPS 实时定轨卡尔曼滤波模型[J]. 武汉大学学报(信息科学版), 2010, 35(6): 653-656.
Inter-Satellite Ranging Augmented GPS Relative Navigation for Satellite Formation Flying
ZHANG Wei1, DU Yao-ke2, LI Dong-jun3, WANG Qiao1,JIN Xiao-jun1, XU Zhao-bin1, JIN Zhong-he1
(1. Micro-Satellite Research Center, Zhejiang University, Hangzhou 310027, Zhejiang, China; 2. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China; 3. Space Star Technology Co. Ltd., Beijing 100086, China)
Aimed at overcoming limitations in navigation accuracy, navigation continuity and real-time performance in pure carrier differential GPS system, an inter-satellite ranging augmented GPS carrier differential relative navigation method was proposed. The integrated relative navigation system contains GPS receivers, inter-satellite ranging sensors and navigation processor which operates in main satellite of the formation flying system. Narrow band communication function is integrated in the inter-satellite ranging sensor, which means it can measure satellite range and transfer GPS data at the same time. Based on extended Kalman filter, the satellite relative position and velocity are real-time computed by applying the simplified dynamic model with GPS and inter-satellite ranging sensor data. The algorithm is validated with data generated by a GPS simulator. Simulation results indicate that the proposed approach is effective for improving navigation accuracy, navigation continuity and real-time performance when the baseline is smaller than 30 km. The achieved real-time navigation accuracy is better than 1 mm; the system can still output the adequate relative range and speed data in a GPS data interrupt; the system initialization time is significantly decreased from tens of epochs to only one epoch.
satellite formation flying; relative navigation; integrated navigation; pseudo range; carrier phase; differential GPS; inter-satellite ranging; extended Kalman filter
1006-1630(2017)03-0095-07
2016-08-28;
2017-03-23
国家自然科学基金资助(60904090,61401389);天地一体化信息技术国家重点实验室(筹)开放基金资助(2014 CXJJ-DH 11);中央高校基本科研业务费专项资金资助(2016QN81007);国家杰出青年基金资助(61525403);国防预研教育部联合基金资助(6141A02033310);上海航天科技创新基金资助(SAST201450)
张 伟(1989—),男,博士生,主要从事星载GPS定轨技术、相对导航技术、GNSS接收机软件设计的研究。
V412.41
A
10.19328/j.cnki.1006-1630.2017.03.013

