卫星通信系统邻星干扰分析方法研究

郭 强,刘 波,司圣平,刘 辉,蒋应富,张 恒

(1.上海航天技术研究院,上海 201109; 2.上海卫星工程研究所,上海 201109)



卫星通信系统邻星干扰分析方法研究

郭 强1,刘 波2,司圣平2,刘 辉2,蒋应富2,张 恒2

(1.上海航天技术研究院,上海 201109; 2.上海卫星工程研究所,上海 201109)

针对多星组网频率复用卫星通信系统的邻星干扰问题，对一种卫星通信系统邻星干扰分析方法进行了研究。首先计算地面站能否同时接收到邻星信号，若无，则不存在邻星干扰，若有，则需分析干扰的影响。其次计算邻星是否在接收天线主波束范围内，若不是，可认为两星的极化方式对接收系统无影响；若是，考虑双星完全重叠的极限情况，分析最严重的邻星干扰，并给出了综合考虑天线、降雨、倾角、冰晶等因素导致的去极化效应的信噪比计算模型。该方法已成功用于我国某卫星星座通信系统设计并通过了在轨测试，误码率满足系统设计要求。研究可为我国其他多星组网频率复用卫星通信系统的研究和设计提供参考。

卫星通信； 邻星干扰； 频率复用； 信噪比； 交叉极化隔离度； 圆极化； 天线主波束； 去极化效应

0 引言

随着我国卫星事业的发展，多颗卫星组网运行实现特定的任务已成为一个趋势。多颗卫星组网会出现同时进入同一地面接收天线接收范围的情况，由于卫星通信系统有其特定工作频段限制，为满足不断增加的传输码速率需求，通信系统工作频段常会出现重叠，在多星组网通信系统设计时须考虑邻星干扰问题，保证多星通信系统的误码率满足组网使用要求。邻星干扰分为使用相同极化方式(单极化或双极化)和使用不同极化方式(双圆极化或双线极化)两种情况。当使用的极化方式相同时，可采用更高进制的调制方式避免频段重叠[1]。但该方法传输每比特数据所需的能量更多，增加了卫星的研制难度和成本，若无法避免频段重叠，则产生同频干扰即邻星干扰，此时需定量计算邻星干扰对系统误码率的影响。当使用的极化方式不同(双圆极化或双线极化)时，全部或部分工作频段重叠，可使传输的码速率最大增加1倍[2-8]。但该法须要解决双极化工作方式下的交叉极化问题，定量计算出交叉极化干扰即邻星干扰对系统误码率的影响。卫星星座组网布局一般为均匀分布，星与星间存在一定距离间隔，则多颗星间的邻星干扰问题可简化为任意两星间的邻星干扰问题。文献[2]对两颗星使用相同单极化方式且不进入接收天线主瓣范围的频率复用卫星通信系统邻星干扰进行了研究；文献[3-9]对单颗星使用双极化频率复用卫星通信系统的交叉极化问题进行了研究，但未见对多颗卫星组网运行时，用相同极化方式(单极化或双极化)和不同极化方式频率复用卫星通信系统进行系统的邻星干扰分析方法的研究。本文从卫星通信系统设计实际出发，以常用的圆极化方式为例，根据ITU-R标准，对多星组网运行时频率复用卫星通信系统邻星干扰的分析方法进行了研究，并成功用于我国某卫星星座频率复用通信系统，为我国多星组网频率复用卫星通信系统的研究与设计提供参考。

1 邻星干扰分析计算方法

多星组网卫星通信系统可包括静止轨道卫星通信系统和非静止轨道卫星通信系统。频率复用则有两个卫星各使用一个相同单极化天线或各使用一个相同双极化天线对地传输数据、两个卫星各使用一个不同的单极化天线对地传输数据等不同方式。本文以常用的圆极化频率复用卫星通信系统为例，讨论了适于以上不同情况的邻星干扰分析方法。

根据组网卫星的轨道类型和参数、地面站的位置，以及接收天线的工作仰角范围，用卫星轨道仿真软件(如STK软件)仿真计算特定地面站能同时接收到两颗卫星下传信号的时间。若该地面站没有被两颗卫星下传信号同时覆盖的时间，即不存在邻星干扰，则按传统的单星通信链路分析方法计算信噪比；若有被同时覆盖的时间，则用本文方法分析邻星干扰的影响[10]。

2 相同极化方式邻星干扰计算方法

如甲、乙两颗卫星采用相同单极化天线，并进入同一接收天线的波束覆盖范围，在接收甲卫星下传信号时，乙卫星在重叠频段内的下传信号会对甲卫星造成干扰，该干扰可视作高斯白噪声，该情况下甲卫星信噪比(Eb/N0)的计算符合信噪比的倒数和原理[1]。其计算公式为

(1)

式中：Etot为甲卫星工作频段的信号总能量；Eover为重叠频段的信号能量；(Eb/N0)s为只有甲卫星条件下的信噪比；(Eb/N0)d为在双星相互干扰时甲卫星的信噪比。

当甲、乙两颗卫星采用相同双极化天线时，目前，因在研和在轨卫星天线的极化隔离度都大于25 dB，两星间的邻星干扰主要为相同单极化方式的同频干扰，不同极化方式间的交叉极化干扰可忽略不计，则计算方法与两颗卫星采用相同单极化天线一致。

3 不同极化方式邻星干扰计算方法

3.1 交叉极化产生原因

在采用双圆极化频率复用技术的卫星通信系统中，交叉极化的产生包括两部分：一是由于卫星天线的馈源极化器制造工艺和安装中不可避免的误差，以及极化变换器的损耗，导致形成的圆极化波不可能是理想的圆形，使系统本身包括交叉极化分量，同时地面接收天线的非理想性也会引入交叉极化分量；二是即使发射端为理想圆极化，在传播过程中，也会受到降雨、倾角、冰晶等因素的去极化影响而引入交叉极化分量。

3.2 交叉极化隔离度定义

一般，用交叉极化隔离度(XPI)度量交叉极化的优劣。双极化通信系统中信号去极化如图1所示。图1中：at，bt为一对正交发射信号；ar，br为对应的正交接收信号；ax，bx为对应的交叉极化分量。XPI的定义为：本信号在本信道接收的共极化分量ar与另一信道在本信道产生的交叉极化分量bx之比[1]。

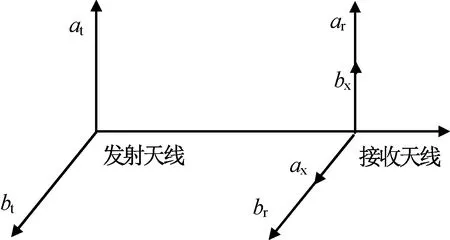
图1 去极化示意Fig.1 Depolarization

通道的交叉极化隔离度可分别表示为

(2)

(3)

对圆极化方式，XPI等于共旋极化分量与反旋极化分量之比。在大多数传播实验中仅有一种极化方式的卫星信号，同时测量接收到的有用信号(共极化)和无用信号(交叉极化)，两者的比值称为交叉极化分辨力(XPD)[1]。有

(4)

通常，计算出的XPI，XPD值相同，并可被简单地称为隔离度[1]。

3.3 圆极化频率复用卫星通信系统邻星干扰分析方法

当特定地面站能同时接收到两颗卫星下传信号时，两颗卫星与同一地面站天线的关系包括两种情况：双星不在同一地面站天线主波束范围内；双星在同一地面站天线主波束范围内。

3.3.1 双星不在同一地面天线主波束范围内

实际的地面站接收天线多为抛物面，则天线的增益G和主瓣宽度θ1/2分别满足关系

(5)

(6)

式中：f为频率；D为天线直径；η为天线效率[1]。

ITU-R标准中对地面站的接收天线旁瓣峰值进行了规定，其天线90%的旁瓣峰值不应大于以下要求

(7)

式中：“*”表示当D/λ小于100时，该角度为(100λ/D) (°)；θ为偏离主波束方向的角度；λ为波长[11-12]。

地面站天线的实际主瓣、旁瓣增益需经过测试，上述理论计算公式可作为系统设计的参考依据。由式(1)，当两颗星的信号不在同一个地面接收天线主瓣范围内，不考虑极化方式时，信噪比计算公式为

(8)

式中：Gmain为接收天线的主瓣增益；Gsub为接收天线的旁瓣增益。

用STK软件仿真计算出同一地面站与两颗卫星所成矢量的夹角，通过调整轨道幅角等参数可改变该矢量夹角的最小值；根据该最小值，以及地面天线的主瓣与旁瓣增益；用式(8)可算出两颗星相互干扰时的最小信噪比，判断所得该信噪比能否满足星地通信的误码率要求，若满足则以该轨道参数作为卫星发射和轨道控制的约束条件。

一般情况下，当双星不在同一个地面接收天线主瓣范围内时，因主瓣增益远大于旁瓣增益，因此两星间的相互干扰很小，不会影响地面站的正常接收，此时两星是否采用不同的极化方式对地面接收系统无影响。

3.3.2 双星在同一地面天线主波束范围内

当通过轨道控制无法实现双星不同时出现在同一地面天线主波束范围内，极限情况为双星完全重叠，此时邻星干扰最大(作为卫星通信系统设计的约束条件)，而其他情况的邻星干扰由于地面接收天线增益的原因均可认为小于该极限情况。该极限情况与单个卫星采用双极化天线的相同，具体分析如下。

a)仅考虑天线导致的去极化效应

根据卫星发射天线和地面站接收天线的轴比，圆极化方式隔离度(XPD)可表示为

DXPD(a)=

(9)

式中：r1，r2分别为卫星天线和地面天线的轴比；α为两者长轴间的夹角[1]。当α=0°时为最小隔离度。±4r1r2项符号的选用原则是：当来波极化方式与接收站本身的极化方式一致时取“+”号；反之取“-”号。

由式(1)，只考虑卫星天线和地面天线导致的去极化效应，邻星干扰信噪比可表示为

(10)

式中：DXPD，min(a)为由式(9)算得的最小隔离度。

b)仅考虑降雨、倾角、冰晶等导致的去极化效应

根据ITU-R标准，假设卫星发射的双圆极化信号为理想圆极化，考虑降雨、倾角、冰晶去极化等因素导致的去极化效应，计算星地通信隔离度的方法如下[13]。

(a)计算随频率变化的项

Cf=30lgf，8GHz≤f≤35GHz

(11)

(b)计算随降雨衰减变化的项

CA=V(f)lgAp

(12)

V(f)=12.8f0.19， 8 GHz≤f≤20 GHz

(13)

V(f)=22.6，20 GHz≤f≤35 GHz

(14)

式中：Ap为所讨论路径上规定的时间百分比p内被超过的降雨衰减值。

(c)计算极化改进因子

(15)

式中：τ为倾角。当τ=45°时，Cτ=0 dB；当τ=0°或90°时，Cτ达到最大值15 dB。其中：τ=45°对应于圆极化。

(d)计算随倾斜角变化的项

(16)

式中：θ为链路仰角。

(e)计算随倾斜角变化的项

(17)

式中：σ为雨滴倾斜角分布的有效标准差。对1%，0.1%，0.01%，0.001%的时间百分比，σ的值分贝相应为0°，5°，10°，15°。

(f)计算雨天p%时间内XPD不大于

(18)

(g)计算随冰晶变化的项

(19)

(h)考虑冰晶影响计算p%时间内的XPD不超过

(20)

计算频率8 GHz以下的XPD时，先计算出频率8 GHz以上的XPD，再用以下计算结果换算到所要的频率

DXPD2=DXPD1-

4 GHz≤f1,f2≤30 GHz

(21)

式中：DXPD1，DXPD2分别为f1(8 GHz以上)，f2(8 GHz以下)频率，以及τ1，τ2极化倾斜角时，相同时间百分比内的XPD值。

c)综合考虑天线和降雨等导致的去极化效应

综合考虑天线的非理想性及降雨等因素导致的去极化效应。根据XPD的定义，共极化分量即有用信号，交叉极化分量即干扰噪声，则计算同一条链路上不同去极化效应产生的总去极化效应，符合信噪比的倒数和原理[8]。有

(22)

则由式(1)，综合考虑天线和降雨等因素导致的去极化效应，计算邻星干扰信噪比的公式为

(23)

4 结束语

随着我国航天事业的快速发展，多颗卫星组网并采用频率复用技术的通信系统将越来越多，邻星干扰问题是整个卫星星座通信系统设计必须解决的关键问题，直接影响整个星座系统的误码率是否能满足用户使用要求。本文基于已有的单星单极化通信系统误码率分析方法、两颗星使用相同单极化方式且不进入接收天线主瓣范围的频率复用卫星通信系统邻星干扰分析方法，以及对单颗星使用双极化频率复用卫星通信系统交叉极化分析方法，提出了多颗卫星组网运行时，对相同极化方式(单极化或双极化)和不同极化方式频率复用卫星通信系统，进行完整系统邻星干扰定量分析的方法。该方法已成功用于我国某多星组网通信系统设计并通过在轨测试，多星通信系统误码率满足用户使用要求。该方法可为我国其他多星组网频率复用卫星通信系统的研究和设计提供参考。

[1] 吕洪生. 实用卫星通信工程[M]. 成都: 电子科技大学出版社, 1994: 53-59.

[2] 刘波. 新一代极轨气象卫星多星在轨运行通信链路的研究与分析[D]. 上海: 上海交通大学, 2013.

[3] 赵宁. 极化复用技术在遥感卫星数据传输中的应用[J]. 航天器工程, 2010, 19(4): 55-62.

[4] 王怀, 李化营, 王涛, 等. 星地一体化极化复用接收实验比对标准研究[J]. 电子测量技术, 2016, 39(2): 8-13.

[5] 周治宇, 黎红武, 田华. 卫星通信系统中降雨的去极化效应估计[J]. 空间电子技术, 2014(1): 77-80.

[6] 王蕾蕾, 李萍, 安合志, 等. Ku波段卫星通信降雨的交叉极化研究[J]. 电子科技, 2012(11): 40-43.

[7] 张莎莎, 刘希刚, 黄缙. 双圆极化频率复用数传链路极化损耗影响分析[J]. 航天器工程, 2012, 21(6): 98-102.

[8] 王万玉, 王永华, 王强. 双圆极化遥感卫星数据接收系统极化鉴别率需求分析[J]. 现代电子技术, 2014, 37(15): 45-54.

[9] YANG Jun-yi, CHEN Jin-shu, WANG Wan-yu, et al. Joint XPI and ISI cancellation for dually-polarized radio systems over earth-space links[J]. Procedia Engineering, 2012, 29: 3217-3221.

[10] 胡国军, 李世忠, 胡海彦, 等. 一种对地观测卫星的数据传输系统及星地链路设计[J]. 遥感应用, 2009(1): 66-74.

[11] Radio Communication Sector of ITU. Radiation diagrams for use as design objectives for antennas of earth stations operating with geostationary satellites: ITU-R S.580-6[S]. Geneva: ITU, 2004.

[12] Radio Communication Sector of ITU. Reference earth-station radiation pattern for use in coordination and interference assessment in the frequency range from 2 to about 30 GHz: ITU-R S.465-5[S]. Geneva: ITU, 1993.

[13] Radio Communication Sector of ITU. Propagation data and prediction methods required for the design of Earth-space telecommunication systems: ITU-R P.618-8[S]. Geneva: ITU, 2007.

Analysis Method Study of Satellite Communications System Adjacent Interference

GUO Qiang1, LIU Bo2, SI Sheng-ping2, LIU Hui2, JIANG Ying-fu2, ZHANG Heng2

(1. Shanghai Academy of Spaceflight Technology, Shanghai 201109, China; 2. Shanghai Institute of Satellite Engineering, Shanghai 201109, China)

Aiming at the problem of adjacent interference of multi satellite communication system with frequency reuse, an analysis method of satellite communication system adjacent interference was studied in this paper. First the ground station could receive satellite signal or not is calculated. There is no adjacent interference if no. It needs to analyze the interference influence if yes. Then the satellite is in the range of the receiving antenna main lobe or not is calculated. The polarization of the two adjacent satellites has no effect on the ground receiving system if no. The limitation when the two satellites are overlap totally shall be in consideration if yes. And the major interference need to be analyzed. Finally the computation mode of signal noise rate is given when the cross polarization is caused by the factors of antenna, rainfall, inclination, ice and others. The method has been successfully applied to the design of a multi-satellite communication system of some satellite in China. The error rate test results meet the design requirements of the system. This method can provide reference for the research and design of China′s other multi-satellite frequency reuse satellite communication system.

satellite communications; adjacent interference; frequency reuse; signal noise rate; cross polarization; circular polarization; antenna main lobe; depolarization effect

1006-1630(2017)03-0131-05

2017-02-13；

2017-03-30

国家重大航天工程

郭 强(1983—)，男，工程师，硕士，主要研究方向为卫星通信系统设计。

V57

A

10.19328/j.cnki.1006-1630.2017.03.018