基于双回路扩展卡尔曼滤波的惯性平台连续自标定
王 琪,汪立新,秦伟伟,沈 强
(火箭军工程大学,西安710025)
基于双回路扩展卡尔曼滤波的惯性平台连续自标定
王 琪,汪立新,秦伟伟,沈 强
(火箭军工程大学,西安710025)
为解决传统的惯性平台连续自标定中,由于系统非线性强、状态向量维数大引起的滤波收敛速度慢、对滤波初始条件敏感等问题,研究了一种双回路扩展卡尔曼滤波方法。首先给出了平台连续自标定的误差模型;然后根据加速度计误差与导航误差之间的关系,对加速度计输出进行预滤波得到加速度计输出误差;同时通过分析陀螺仪误差在平台连续自标定过程中的传播特性,将耦合在加速度计输出误差中的陀螺仪误差解耦;最后以陀螺仪误差和加速度计输出为观测量,建立了陀螺仪和加速度计的扩展卡尔曼滤波方程,分别对陀螺仪和加速度计误差系数进行标定,实现双回路扩展卡尔曼滤波。仿真结果表明,该方法能够在900 s内以低于0.05%的相对误差标定出所有的平台误差系数,并且对滤波初始条件不敏感,可以有效地扩展连续自标定方法的实际应用。
连续自标定;扩展卡尔曼滤波;惯性平台;误差模型;误差解耦
0 引 言
制导工具误差是影响制导武器命中精度的主要因素,而惯性仪表的误差是制导工具误差中的主要成分,因此在使用时必须进行补偿。根据陀螺仪和加速度计在长期稳定性测试中一次启动随机误差远小于多次启动误差的特性,提出了平台射前自标定[1]。传统的多位置自标定方法是一种“静态”的标定方法,由于其误差模型相对简单,特别是激励安装误差的地球自转角速度相对较小,导致多位置自标定中对于安装误差的激励不够充分,标定精度较低[2-3]。
针对多位置自标定的缺点,Jackson[4]提出了连续自标定方法。惯性平台连续自标定方法的基本原理如下:惯性平台在外力矩的作用下以角速度ωc(称为加矩角速度)转动,在地球自转角速度、加矩角速度以及重力加速度的激励下,加速度计输出中包含有陀螺仪误差、加速度计误差、安装误差和平台对准误差等全部误差信息。以加速度计输出为观测量,以平台对准误差方程为动力学模型,采用最优滤波算法估计平台误差系数和对准误差[5]。文献[6]系统地介绍了平台连续自标定的误差建模、可观测性分析、参数辨识等内容;文献[7-8]针对大失准角情况下传统的失准角误差模型会产生较大误差的问题,建立了框架角误差模型;文献[9-10]分别建立了以加速度计输入轴和陀螺仪输入轴为基准的平台坐标系,使所有的安装误差变得可观,提高了标定精度。
但是由于平台连续自标定的误差模型复杂、误差系数较多[11],因此在建立滤波模型时,会存在状态向量维数大、系统非线性强等特点,这会导致在滤波过程中收敛速度慢、对滤波初始条件比较敏感等问题,从而限制了连续自标定方法的实际应用。针对以上问题,本文研究了一种基于双回路扩展卡尔曼滤波的惯性平台连续自标定方法,以提高连续自标定方法的适用性。
1 坐标系定义
首先给出平台中的坐标系定义,假设平台由三个单自由度积分陀螺仪与三个摆式加速度计组成,如图1所示。
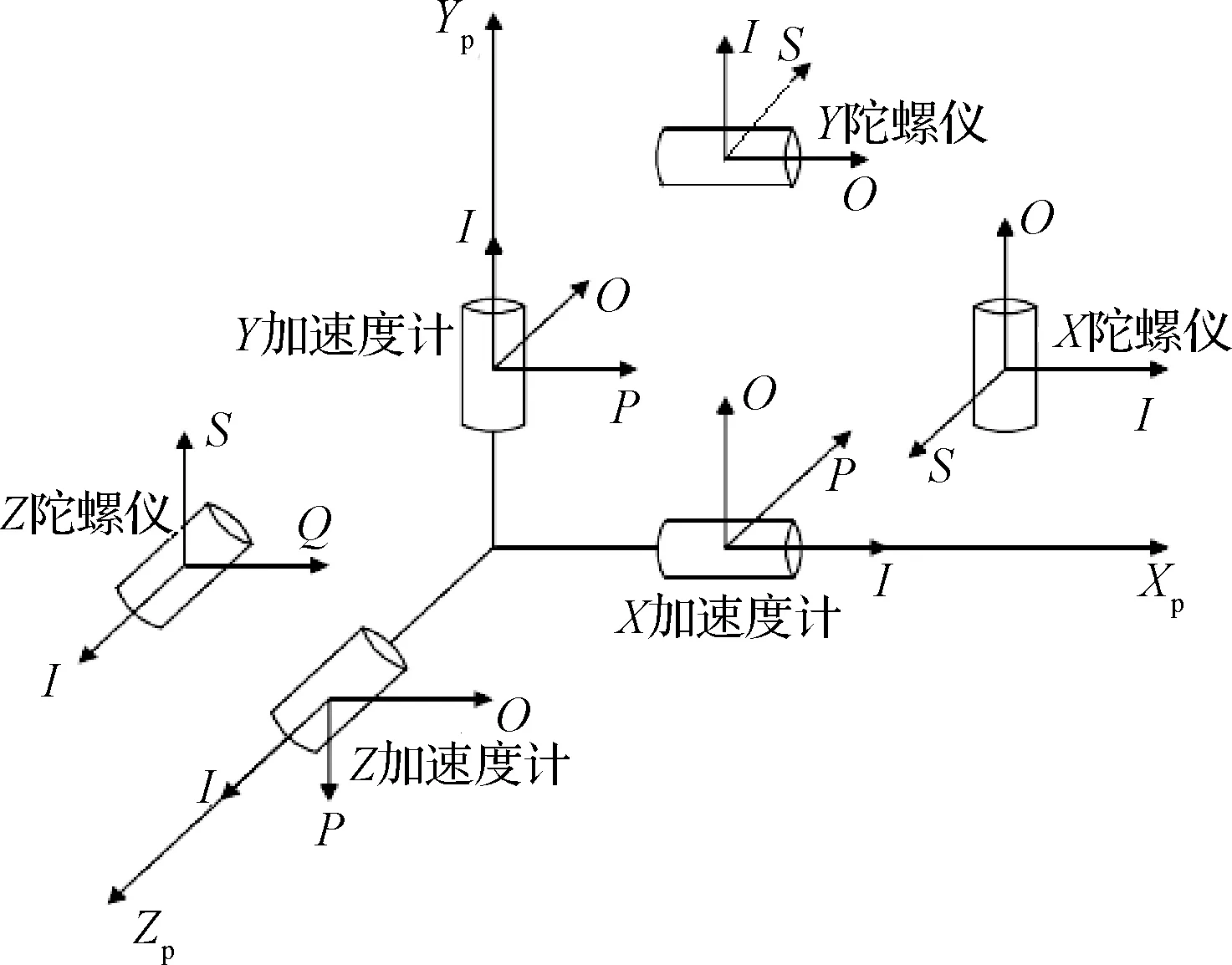
图1 平台陀螺仪和加速度计安装示意图Fig.1 Installation diagram of gyros and accelerometers in platform
设陀螺仪I轴绕其O、S轴的安装误差为Δoi、Δsi(i=x,y,z),如图2所示。则平台坐标系(p)到陀螺仪敏感轴坐标系(g)的转换矩阵为[12]
(1)
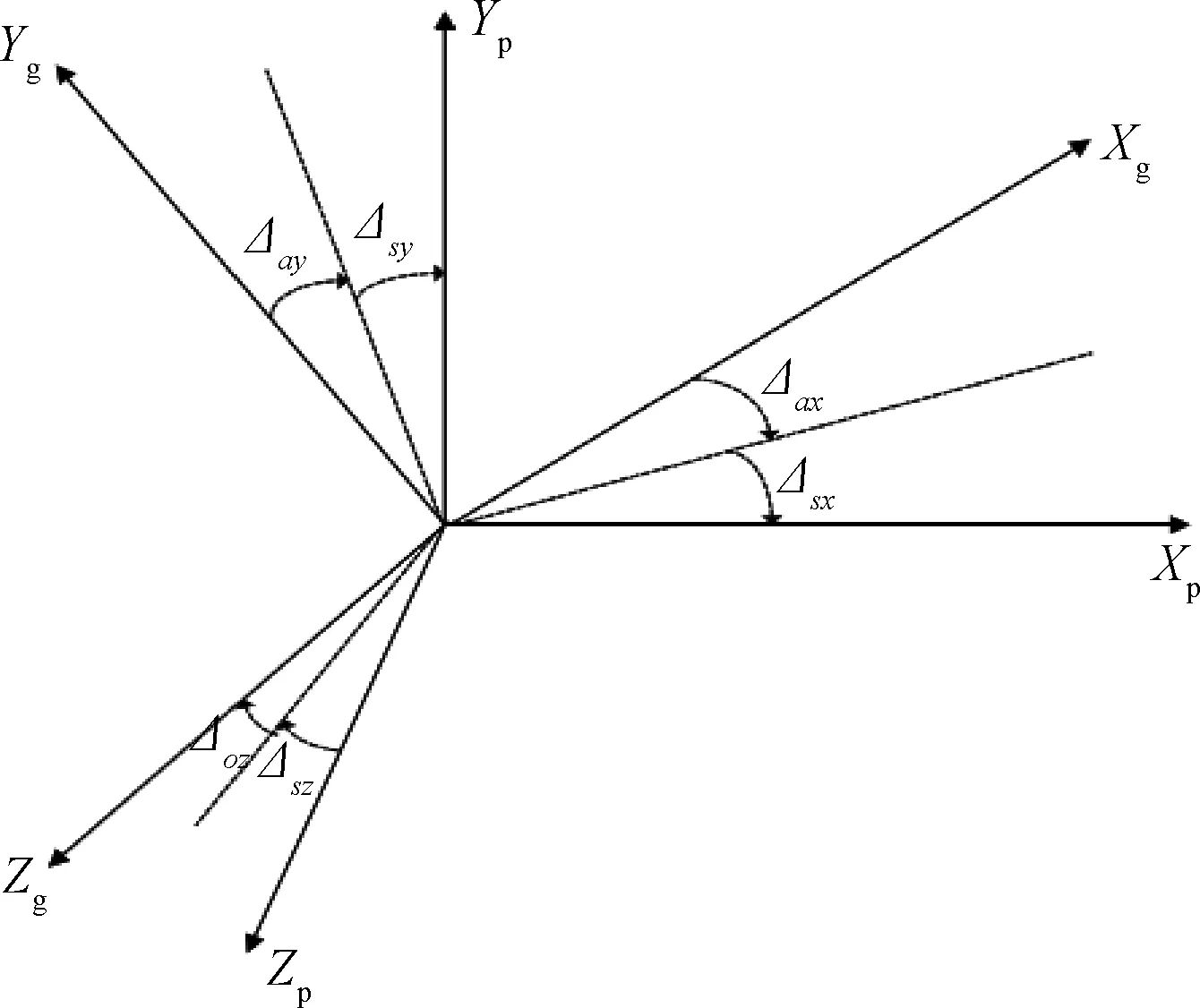
图2 陀螺仪安装误差Fig.2 Gyro-platform geometry
如图3所示,设加速度计I轴绕其P、O轴的安装误差为θpi、θoi(i=x,y,z),则p系到加速度计敏感轴坐标系(a)的转换矩阵为[12]
(2)
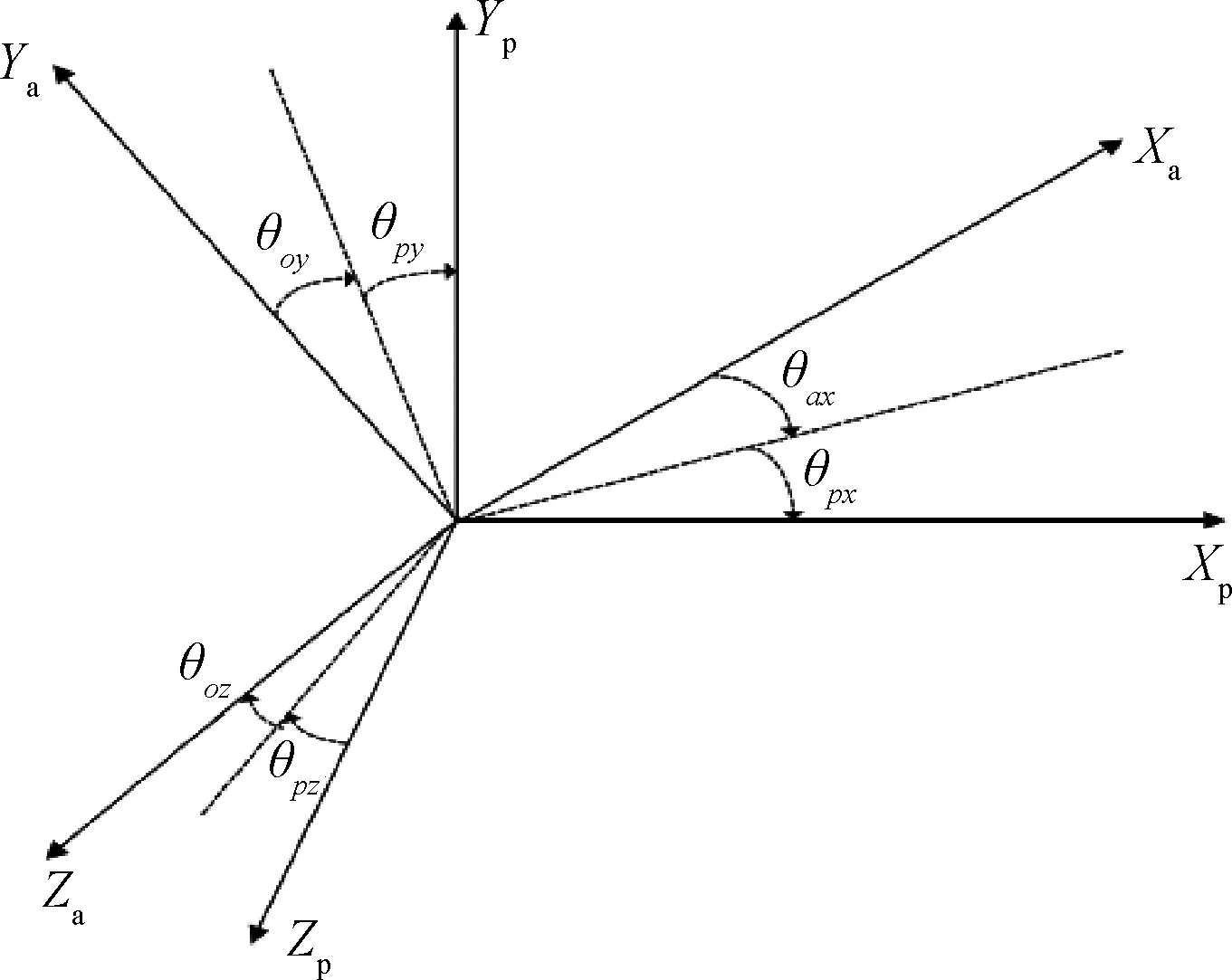
图3 加速度计安装误差Fig.3 Accelerometer-platform geometry
此外,定义一个理想计算坐标系(c):计算坐标系是一个理想的正交坐标系,作为平台连续转动的参考。在不考虑任何漂移的情况下,计算坐标系与平台坐标系重合。
2 连续自标定误差模型
2.1 姿态误差方程
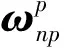
(3)
(4)
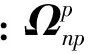
将式(4)代入式(3),有
(5)
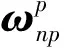
(6)
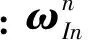
对式(6)左乘Φn,有
(7)
利用列向量φ、ω与其反对称矩阵Φ、Ω之间的性质Ωφ+Φω=0,式(7)可变换为
(8)
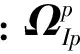
对式(5)右乘φn,并将式(8)代入可得
(9)
对式(9)左乘(Φn)-1并省略高阶项,整理可得失准角误差方程为
(10)
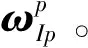
综上所述,p系相对I系的转动角速度为
(11)
将式(11)代入式(10)可得平台连续自标定的姿态误差方程为
(12)
2.2 陀螺仪误差模型
陀螺仪的误差与其三轴上的比力有关,其误差模型为[15]
i = x,y,z
(13)
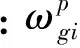
陀螺仪三轴上的比力如下式所示
(14)
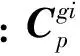
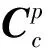
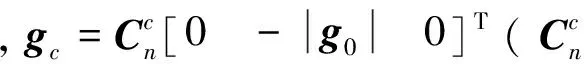
将式(14)代入式(13)可得陀螺仪误差模型为
(15)
式中:
2.3 加速度计输出模型
加速度计的输出与加速度计三轴敏感到的比力有关,加速度计三轴上的比力为
(16)
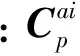
加速度计输出模型为[15]
(17)
式中:ka0i为加速度计的零偏;ka1i为加速度计一次项误差系数;同理,未考虑加速度计二次项误差系数;εai为测量随机误差。
将式(16)代入式(17)并忽略加速度计误差系数相乘形成的二阶项,可得加速度计输出模型为
Za=Cφ+D1ka+D2θ+h(ka,φ)+gc+εa
(18)
式中:
3 误差解耦
为实现双回路滤波,本文选择陀螺仪误差和加速度计输出两个观测量来分别对陀螺仪和加速度计误差系数进行辨识。因此需要将耦合在加速度计误差中的陀螺仪误差进行解耦。为此首先分析陀螺仪误差在平台连续自标定中对加速度计输出的影响。
3.1 陀螺仪误差传播分析
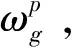
图4 陀螺仪误差对加速度计输出的影响Fig.4 Effect on accelerometers’ output of gyros’ error
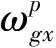
由此可知,只有沿Xp和Zp轴方向(即水平方向)的陀螺仪误差会引起加速度计误差,而沿Yp轴方向(即天向)的陀螺仪误差不会对加速度计误差产生影响。
3.2 误差解耦
根据第3.1节得到的结论,可以采取如下的解耦方法从加速度计误差中得到陀螺仪误差:
(19)
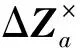
yL的东向和北向分量即为陀螺仪滤波回路的量测更新,即有
(20)
式中:e和n分别为东向和北向的3×1的单位向量,由n系到c系的方向余弦组成。
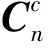
(21)
4 加速度计输出预滤波
在平台连续自标定中,加速度计输出是唯一的输出量,因此需要对加速度计输出进行预滤波来得到加速度计误差。加速度计误差ΔZa与导航速度误差Δv有如下关系[18]
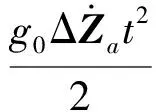
(22)
式中:Δv0为初始误差。
速度误差可由加速度计输出减去理论输出得到。理论上加速度计测量的是重力加速度在p系的投影,而在不考虑误差的情况下,p系与c系重合,因此加速度计理论输出为重力加速度在c系的投影,由此可得速度误差为[18]
Δv=Za-gc
(23)
需要注意的是,式(23)中的Za是加速度计输出转换成的比力值。
设滤波周期为T,加速度计输出离散周期为ΔT,则式(22)的离散形式可以写为
(24)
式中:j∈[-N,N],N=T/ΔT。
根据最小二乘法可解得加速度计误差分量为
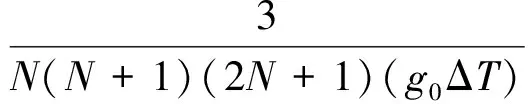
(25)
5 双回路扩展卡尔曼滤波
通过第3节的误差解耦和第4节的加速度计输出预滤波,得到的陀螺仪误差可以作为陀螺仪滤波回路的量测更新,同时将加速度计输出作为加速度计滤波回路的量测更新,就可以实现双回路卡尔曼滤波,从而极大地减小滤波过程中的计算量和加快滤波收敛速度。
5.1 陀螺仪滤波方程
(26)
式中:T为滤波周期,k表示第k个滤波周期。

(27)
5.2 加速度计滤波方程
(28)
对式(18)进行离散化可得观测方程为
Cφk+1+D1kak+1+D2θk+1+
h(ka,k+1,φk+1)+gc,k+1+εa,k+1
(29)
在得到陀螺仪和加速度计的滤波方程后,就可以利用扩展卡尔曼滤波分别对陀螺仪和加速度计的误差系数进行辨识,从而实现基于双回路扩展卡尔曼滤波的惯性平台连续自标定。
扩展卡尔曼滤波的基本方程如式(30)所示,式中:Qk是系统噪声协方差矩阵,Rk为量测噪声协方差矩阵,F和H分别为fe(X)和he(X)对X的偏导数。
(30)
6 仿真分析
根据前文推导的滤波方程,对本文方法进行了仿真验证。首先设置仿真初始条件如下:
1)在连续自标定开始之前,平台处于空间稳定的工作状态,即始终跟踪当地水平面;
2)滤波周期为T=0.25 s;
3)加速度计量测噪声为1×10-6m/s2;
4)滤波初值设置为0。
由于平台误差系数的量值相对较小,因此定义如下的相对误差来表示误差系数的标定精度。
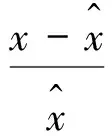
(31)
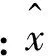
陀螺仪误差系数标定结果如图5所示,加速度计误差系数标定结果如图6所示。从图中可以看出,本文方法可以在900s内标定出所有的陀螺仪和加速度计误差系数,而且相对误差都小于0.05%,验证了方法的有效性。同时可以注意到,部分误差系数,特别是安装误差的滤波值在滤波稳定后会出现周期性的波动,在图中表现为一些周期性的“尖刺”,这是因为当加速度计接近水平位置时,加速度计输出中噪声比很大,从而会造成滤波结果偏离真值,在实际操作中甚至有可能导致滤波结果发散,这种情况是需要避免的。具体做法是:当加速度计接近水平位置时,断开陀螺仪和加速度计滤波回路的量测更新,待加速度计离开水平位置一定角度后,再重新获取量测更新值,继续进行滤波。
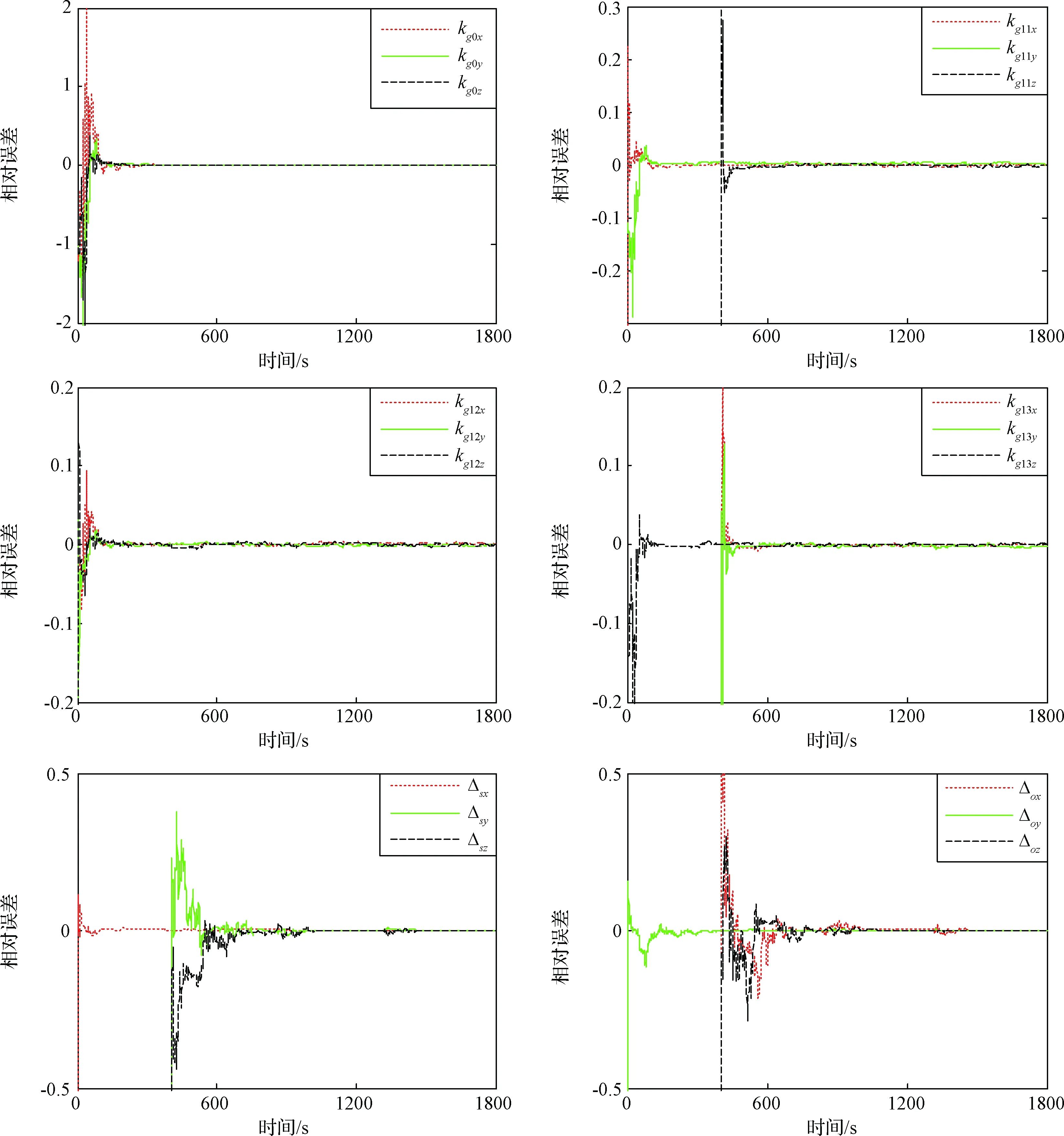
图5 陀螺仪误差系数标定结果Fig.5 Calibration results of gyros’ error coefficients
为验证本文方法滤波收敛速度快、对初始条件不敏感的优点,将本文方法与文献[6]中的方法进行了仿真对比。设置了如下不同的滤波初始条件:
(1)加速度计量测噪声设置为1×10-6m/s2,滤波初值设置为0;
(2)加速度计量测噪声设置为1×10-6m/s2,滤波初值设置为X0/2(X0为仿真真值);
(3)加速度计量测噪声设置为1×10-6m/s2,滤波初值设置为X0+N(0,1)·X0(N(0,1)为服从均值为0、方差为1的正态随机数);
(4)加速度计量测噪声设置为1×10-4m/s2,滤波初值设置为0。
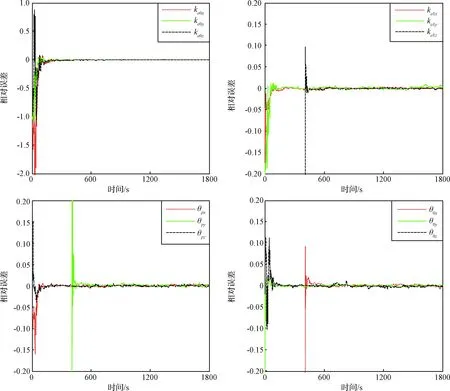
图6 加速度计误差系数标定结果Fig.6 Calibration results of accelerometers’ error coefficients
不同初始条件下各参数的滤波收敛速度见表1,由于标定参数较多,表中只给出了所有参数收敛的最终时间。

表1 不同初始条件下的滤波收敛时间Table 1 Convergence time of different filter initial condition
从表1可以看出,本文方法在初始条件(1)、(2)、(3)下的滤波收敛速度明显快于文献[6]方法。在标定精度方面,本文方法在三种初始条件下的标定相对误差都低于0.05%,而文献[6]方法的相对误差都在0.1%~1%之间。在初始条件(4)下,随着量测噪声的增大,文献[6]方法中的陀螺仪安装误差系数Δsy、Δsz、Δox和Δoz不能有效的收敛到真值,而本文方法的标定结果基本不受影响。验证了本文方法滤波收敛速度快、对初始条件不敏感的优点。
7 结 论
针对传统的连续自标定方法中,由于系统非线性强、状态向量维数大,会引起滤波收敛速度慢、对初始条件敏感等问题,本文研究了一种基于双回路扩展卡尔曼滤波的惯性平台连续自标定方法,以陀螺仪误差和加速度计输出为观测量,将陀螺仪和加速度计分为两个回路进行滤波,从而降低滤波方程中的状态向量维数和系统的非线性。仿真结果表明,该方法可以加快连续自标定的滤波收敛速度和降低对滤波初始条件的敏感度,有效地提高连续自标定方法的适用性。
[1] 钟万登.液浮惯性器件[M].北京:宇航出版社,1994:348-350,371-372.
[2] 杨立溪.惯性平台误差快速自标定技术[J].中国惯性技术学报,2000,8(4):1-4.[Yang Li-xi. Rapid autocalibration for the errors of inertial platform [J]. Journal of Chinese Inertial Technology, 2000, 8(4): 1-4.]
[3] 孟卫锋,袁爱红,贾天龙,等.高精度惯性平台十六位置自标定方案[J].中国惯性技术学报,2015,23(2):150-155.[Meng Wei-feng, Yuan Ai-hong, Jia Tian-long, et al. 16-position self-calibration of high-accuracy inertial platform [J]. Journal of Chinese Inertial Technology, 2015, 23(2): 150-155.]
[4] Jackson A D. Continuous calibration and alignment techniques for an all-attitude inertial platform [C]. AIAA Guidance and Control Conference, Key Biscayne, Florida, USA, August 20-22, 1973.
[5] Cao Y, Cai H, Zhang S F, et al. A new continuous self-calibration scheme for a gimbaled inertial measurement unit [J]. Measurement Science and Technology, 2012, 23(1): 385-394.
[6] 杨华波.惯性测量系统误差标定及分离技术研究[D].长沙:国防科学技术大学研究生院,2008.[Yang Hua-bo. Research on error calibration and separation for inertial measurement systems [D]. Changsha: Graduate School of National University of Defense Technology, 2008.]
[7] 曹渊,张士峰,杨华波,等.惯导平台误差快速自标定方法研究[J].宇航学报,2011,32(6):1281-1287.[Cao Yuan, Zhang Shi-feng, Yang Hua-bo, et al. Research on rapid self-calibration method for inertial platform [J]. Journal of Astronautics, 2011, 32(6): 1281-1287.]
[8] 丁智坚,蔡洪,杨华波,等.浮球式惯性平台连续翻滚自标定自对准方法[J].国防科技大学学报,2015,37(3):148-154.[Ding Zhi-jian, Cai Hong, Yang Hua-bo, et al. Continuous self-calibration and self-alignment method for floated inertial platform [J]. Journal of National University of Defense Technology, 2015, 37(3): 148-154.][9] 许永飞,张士峰.惯导平台自标定中安装误差可观性分析[J].中国惯性技术学报,2015,23(5):575-579.[Xu Yong-fei, Zhang Shi-feng. Observability analysis of IMU’s misalignment angles in self-calibration for inertial platform [J]. Journal of Chinese Inertial Technology, 2015, 23(5): 575-579.]
[10] 连丁磊,夏刚,王汀,等.基于陀螺仪敏感轴系的平台连续翻滚自标定算法[J].导弹与航天运载技术,2013,2:24-29.[Lian Ding-lei, Xia Gang, Wang Ting, et al. Self-calibration algorithm of inertial navigation platform continuous tumble based on gyro sensitive shaft system [J]. Missiles and Space Vehicles, 2013, 2:24-29.]
[11] 杨华波,蔡洪,张士峰,等.高精度惯性平台误差自标定自对准技术[J].宇航学报,2006,27(4):600-604.[Yang Hua-bo, Cai Hong, Zhang Shi-feng, et al. Continuous calibration and alignment techniques for a high precision inertial platform [J]. Journal of Astronautics, 2006, 27(4): 600-604.]
[12] Chana K Y, Rajakarunaa N, Engelkeb U, et al. Alignment parameter calibration for IMU using the Taguchi method for image deblurring [J]. Measurement, 2015, 65: 207-219.
[13] 曹渊,张士峰,杨华波,等.一种新的惯性平台快速连续旋转自对准方法[J].兵工学报,2011,32(12):1468-1473.[Cao Yuan, Zhang Shi-feng, Yang Hua-bo, et al. Fast self-alignment method for inertial platform through continuous rotation [J]. Acta Armamentarii, 2011, 32(12): 1468-1473.]
[14] Drora G M, Itzhack Y B I. Unified approach to inertial navigation system error modeling [J]. Journal of Guidance Control and Dynamics, 1992, 15(3): 648-653.
[15] 包为民,申功勋,李华滨.惯性平台在系统中多位置翻滚自标定方法[J].北京航空航天大学学报,2011,37(4):462-465.[Bao Wei-min, Shen Gong-xun, Li Hua-bin. Investigation on inertial platform multi-position rolling self-calibration [J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(4): 462-465.]
[16] 王琪,汪立新,秦伟伟,等.基于D-最优的惯性平台自标定方案设计[J].中国惯性技术学报,2016,24(5):583-588.[Wang Qi, Wang Li-xin, Qin Wei-wei, et al. Design of inertial platform self-calibration scheme based on D-optimal theory [J]. Journal of Chinese Inertial Technology, 2016, 24(5): 583-588.]
[17] 任磊,杜建邦,王美娥.旋转惯导中加速度计尺寸效应误差分析及补偿[J].航空学报,2013,34(6):1424-1435.[Ren Lei, Du Jian-bang, Wang Mei-e. Error analysis and compensation of size effect in INS with IMU rotation [J]. Acta Aeronautica et Astronautica Sinica, 2013,34(6):1424-1435.]
[18] 秦永元.惯性导航[M].科学出版社,2006:249-253.
通信地址:陕西省西安市灞桥区同心路2号3304分队(710025)
电话:15829247083
E-mail:wq050314@163.com
秦伟伟(1982-),男,讲师,主要从事高超声速飞行器研究。本文通信作者。
通信地址:陕西省西安市灞桥区同心路2号3304分队(710025)
电话:18502967140
E-mail:18502967140@163.com
Continuous Self-Calibration of Inertial Platform Based on Dual Extended Kalman Filter
WANG Qi, WANG Li-xin, QIN Wei-wei, SHEN Qiang
(Rocket Force University of Engineering, Xi’an 710025, China)
In view of the problems of slow convergence and sensitivity to initial conditions in the traditional continuous self-calibration of an inertial platform because of the nonlinearity of the system and the large number of dimensions of the state vector, the dual extended Kalman filter is researched in this paper. Firstly, the error models of the continuous self-calibration are given. Then the output error of the accelerometer is pre-filtered according to the relationship between the accelerometer error and the navigation velocity error. At the same time, the gyro error is decoupled from the output error of the accelerometer by analyzing its propagation characteristics in the continuous self-calibration. At last, the dual extended Kalman filter is carried out by using the gyro error and the accelerometer output as the observations respectively to establish the filter equations of the gyro and the accelerometer, which can reduce the nonlinearity of the system and the number of the dimensions of the state vector. Simulation results indicate that the continuous self-calibration method based on the dual extended Kalman filter can calibrate all the error coefficients of the inertial platform with relative error lower than 0.05% within 900s and is not sensitive to the initial conditions, which is beneficial to the application of the continuous self-calibration of the inertial platform.
Continuous self-calibration; Extended Kalman filter; Inertial platform; Error model; Error decoupling
2017-03-13;
2017-04-19
国家自然科学基金青年基金(61503390,61503392);陕西省自然科学基金(2015JQ6213);航空科学基金(201501U8001)
U666.12
A
1000-1328(2017)06-0621-09
10.3873/j.issn.1000-1328.2017.06.009
王 琪(1991-),男,博士生,主要从事惯性系统及仪器研究。

