一种基于角度偏离的卫星分系统异常检测方法

康 旭，皮德常，田华东

(1. 南京航空航天大学计算机科学与技术学院，南京211106)(2.中国空间技术研究院总体设计部，北京100094)



一种基于角度偏离的卫星分系统异常检测方法

康 旭1，皮德常1，田华东2

(1. 南京航空航天大学计算机科学与技术学院，南京211106)(2.中国空间技术研究院总体设计部，北京100094)

为保证卫星稳定运行，延长卫星寿命，提出一种基于角度偏离的卫星异常检测算法(ADMAD)。针对卫星遥测数据构成的高维数据空间，利用共享近邻(SNN)算法构建相关数据集空间，用角度代替距离，采用基于角度偏离的属性选择算法筛选与异常相关的属性，使用归一化的马氏距离计算异常值，结合统计学知识计算得到异常阈值并对数据集进行分类。采用某卫星2014年7-9月、2015年7-9月控制和电源分系统的遥测数据分别进行验证，试验结果表明，在领域知识匮乏的情况下，该算法的准确率可以达到95%以上，算法鲁棒性较高，能够有效地实时检测卫星分系统异常。

卫星分系统；角度偏离；属性选择；异常检测

0 引 言

卫星是一种融合遥感、通信、计算机科学等多学科技术研制出来的多功能系统，它是人类探索宇宙奥秘的首要途径。由于太阳辐射、外太空温差变化大等多种因素，卫星在轨运行期间会出现各种各样的异常或故障[1-2]，及时发现和避免这些异常和故障能够保证卫星运行的可靠性和安全性，延长卫星使用寿命。因此，异常检测在卫星故障排查和实时健康检测等领域起着重要的作用。

传统的异常检测算法是基于距离的异常检测算法，这类算法能够在较短的时间内检测出局部异常，但是随着数据维度的增加，计算距离所消耗的成本增加，因此基于距离的异常检测算法具有较大的局限性，不能从低维数据空间扩展到高维数据空间。Kriegel[3]指出“在高维空间中，角度比距离更稳定”。因此，在高维数据空间中可以用角度代替距离。Kriegel等[4]在2008年KDD国际会议上提出了一种基于角度的异常检测算法(Angle-based outlier detection,ABOD)，该算法通过计算数据记录的角度方差来衡量其是否发生异常。然而，由于该算法需要扫描全局数据记录，故算法复杂度为O(dn3)，效率很低。为解决复杂度高的问题，Pham和Pagh[5]提出了一种接近线性时间复杂度的角度异常检测算法，该算法的时间复杂度为O(nlogn(d+logn))。随后，Ye等[6]提出了一种增量式的基于角度的异常检测算法，算法时间复杂度为O((ylogk+mlogk)·n+(x+y)·(mr+mk+k2+kr)+mkr+mk2)，缩短了计算时间，提高了效率。这两种算法虽然效率较高，但仍然没有达到卫星异常检测实时性要求。

已有的卫星异常检测方法大多需要借鉴相关的领域知识，而本文在上述研究的基础上，提出了一种无领域知识的基于角度偏离的卫星分系统异常检测算法(Anomaly detection method based on angle deviation，ADMAD)，该算法采用滑动窗口技术和共享近邻算法构建相关数据集空间，缩小了搜索空间，大大缩短了计算时间，同时使用一种基于角度偏离的方法来选择特征属性及构建特征属性空间。在领域知识匮乏的情况下，通过计算异常值，避免了某些与异常不相关的属性对异常检测结果的影响。

1 构建相关数据集空间

由于卫星的异常通常为突发情况，判断遥测数据是否发生异常，与该遥测数据前某一时间段之内的遥测数据有关[7]，而与其时间点相差较远的遥测数据无关。因此，本文引入了滑动窗口机制，通过滑动窗口提取某条遥测数据之前一段时间的遥测数据作为该条遥测数据的异常分析子数据集，在子数据集中计算该条遥测数据的异常值，缩小了异常分析的数据量，大大提高了算法效率，对卫星实时异常检测具有重要的意义。

当滑动窗口较大时，算法的搜索空间依然很大，达不到减小搜索空间，提高算法效率的目的。故可以通过K近邻算法[8]在滑动窗口内提取数据记录的近邻数据记录空间，在此空间中执行异常检测算法。然而，在高维数据空间中，距离和邻域的概念失去了原始意义，因此，本文采用了一种在高维数据空间普遍采用的替代算法，共享最近邻(Shared nearest neighbors, SNN)算法。

SNN算法最早是由Jarvis和Patrick[9]提出。如果两个数据对象越相似，则它们共享的最近邻个数越多。计算两条数据记录的共享近邻相似度即统计这两条数据记录的共享近邻个数。假设原始数据空间为D⊆d，滑动窗口为W⊆d，在空间W中任意一点p，点p的K近邻数据集为Nk(p)，空间W中另一点q的K近邻数据集为Nk(q)，则SNN相似度为：

(1)

式中：f(·)函数用于统计数据集Nk(p)和Nk(q)中相同元素的个数。

基于SNN算法的基本思想，本文可以选择点p的SNN相似度最大的s个数据记录构成其最近邻子空间即为相关数据集空间，记作R(p)，其中s≤k。

2 筛选特征属性

所谓异常，即某一个数据记录不同于其他数据记录，如图1(a)所示。针对选择特征参数的重要性，本文提出一种基于角度偏离的属性选择算法。如图1(b)所示，数据记录p的最近邻子空间的中心为q(用黑色三角形表示)，线段l是p与q的连线，这里用这条线段表示数据记录p与其最近邻子空间的偏离程度，该线段分别与x轴方向和y轴方向形成两个夹角α和β，α小于β。显然，与线段l有较小偏离角度的坐标轴方向上出现了异常，而与线段l有较大偏离角度的坐标轴方向上没有出现异常。正如图1(b)所示，使用基于角度偏离的属性选择算法，x轴对应的属性会被作为特征属性保留下来。

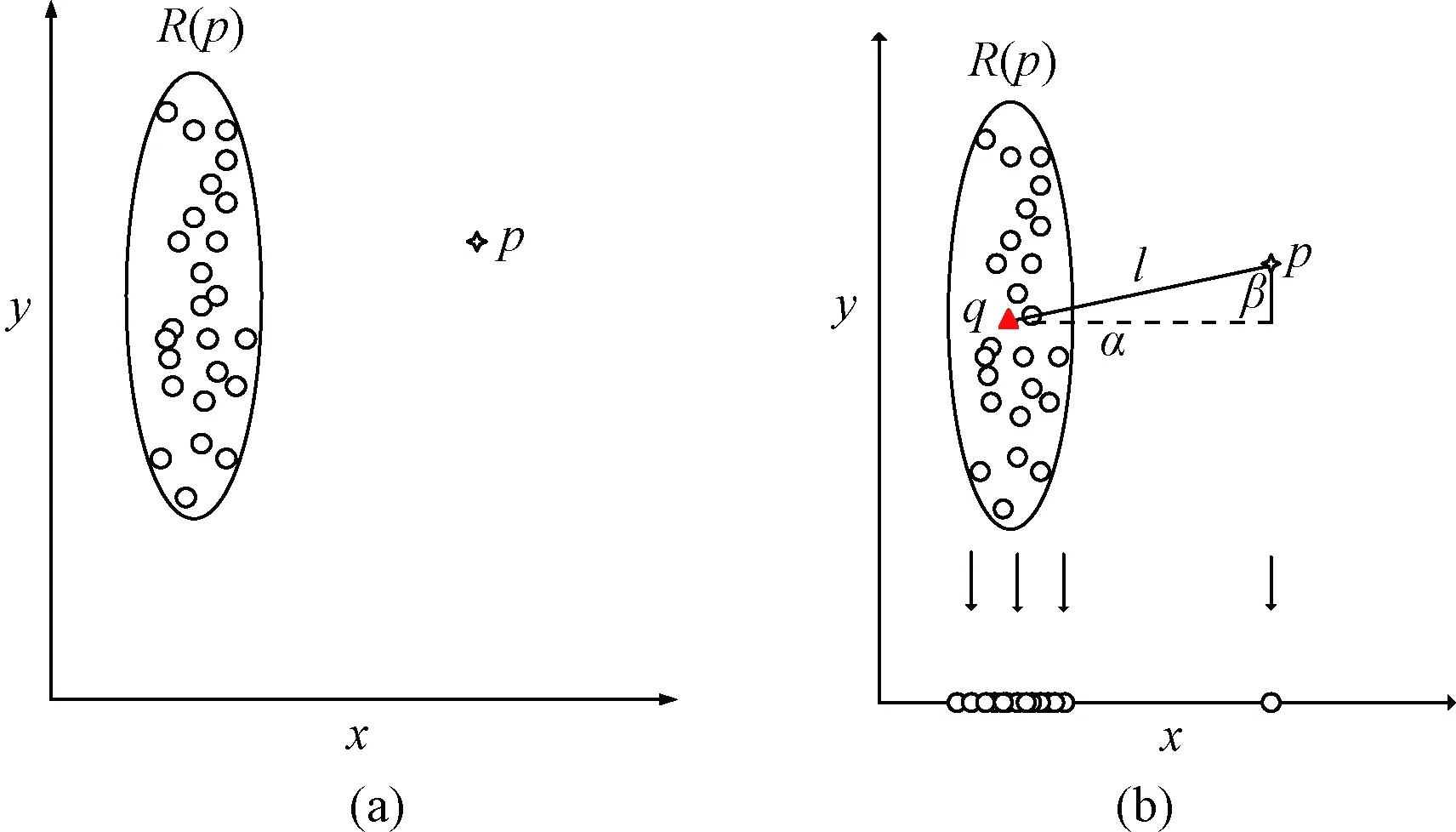
图1 相关数据集空间映射Fig.1 Mapping of reference point sets

2.1 计算角度偏差余弦值的平均值

令μd(j),j∈N,表示在d维空间中与第j维属性方向平行的单位向量。向量Vp是数据记录p的表示向量，Vq是数据记录p的最近邻空间的中点q的表示向量，向量Vq可以用数据记录p的最近邻空间中所有点的表示向量的均值来代替。则数据记录p与q之间的连线l的表示向量为l=Vp-Vq，记为l=[l1,l2,…,ld]T，则直线l与每一维属性方向平行线之间的夹角余弦值为：

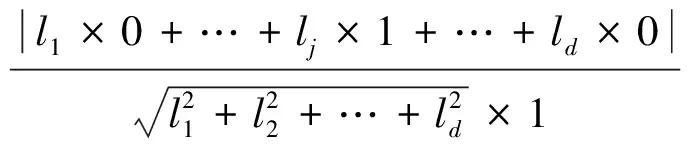
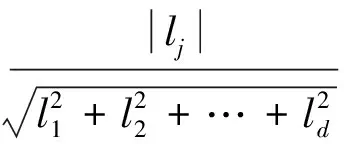
(2)

如果有多个属性与异常相关且第j个属性是与异常相关的属性，在计算数据记录p与第j维向量夹角的余弦绝对值时，由于其他与异常相关属性的影响使得夹角的余弦值偏小，不能将属性j正确提取出来。因此，为降低其他与异常相关属性对属性j的影响，将计算数据记录p与第j维向量夹角的余弦绝对值的过程分解为在所有包含j的二维空间中，计算数据记录p与第j维向量夹角的余弦绝对值的平均值，计算式如下：

(3)

式中：d表示向量空间维度，j-表示不同于j的属性，所有包含j的二维空间的个数为d-1。

式(3)中，当属性j和j-均为与异常无关的属性时，则lj与lj-的数值可能均为0，此时式(3)的分母为0，无意义。因此，为了消除分母为0的影响，本文将连线l中等于0的分量用一个极小的常数ε=10-5来代替。

(4)

则，式(4)转变为：

(5)

A(l,μd(j))值越大，属性j与异常相关程度越大，属性j应该被保留;否则，A(l,μd(j))值越小，属性j与异常相关程度越小，属性j应该被舍弃。

2.2 确定筛选阈值

角度偏差余弦值的平均值A在高维空间中是一种相对鲁棒性的度量标准，故本文设置一个阈值来筛选特征属性，阈值的计算式为：

(6)

(7)

3 计算异常检测值

对于某一数据记录i，在任意属性j上的A值均小于阈值T，这说明数据记录i在任何属性维度上都不明显偏离其最近邻子空间。因此，可以判定数据记录i不是异常数据记录。故本文定义对于所有属性j∈N都有Hi(j)=0的数据记录的异常检测值为0。

在马氏距离的基础上，为适应卫星遥测数据的特点，本文采用归一化的马氏距离来计算异常可疑点偏离其最近邻子空间的程度即异常检测值，计算数据记录i在d维数据空间的异常检测值S(i)，计算式如下：

S(i)=

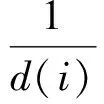
(8)

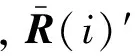
统计分析发现S满足自由度为d-1的χ2分布，因此本文选择S所形成的χ2分布上概率为α的对应值作为异常检测值的阈值，α取99.9%。同时，也可以使用一个简单的分类器对S进行分类，将S值较高的数据记录分为异常数据记录，而S值较低的数据记录分为正常数据记录。

4 实 验

实验数据是某卫星控制和电源分系统2014年7月1日-2014年9月30日和2015年7月1日-2015年9月30日的遥测数据，共包含76个遥测参数，约1600万条记录。本实验包含4个阶段，分别为：数据预处理、采用SNN算法构建每个数据记录的相关数据集空间、筛选每个数据记录的特征属性、使用归一化的马氏距离计算异常检测值并进行异常检测，具体的操作流程如图2所示。

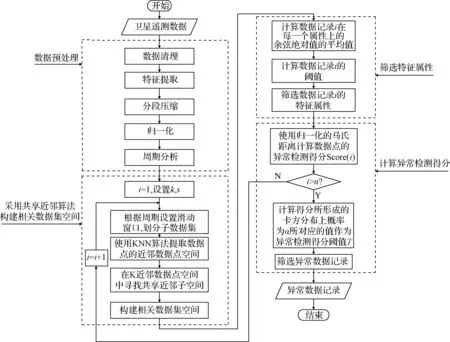
图2 基于角度偏离的异常检测模型框架Fig.2 Frame of anomaly detection model based on angle deviation

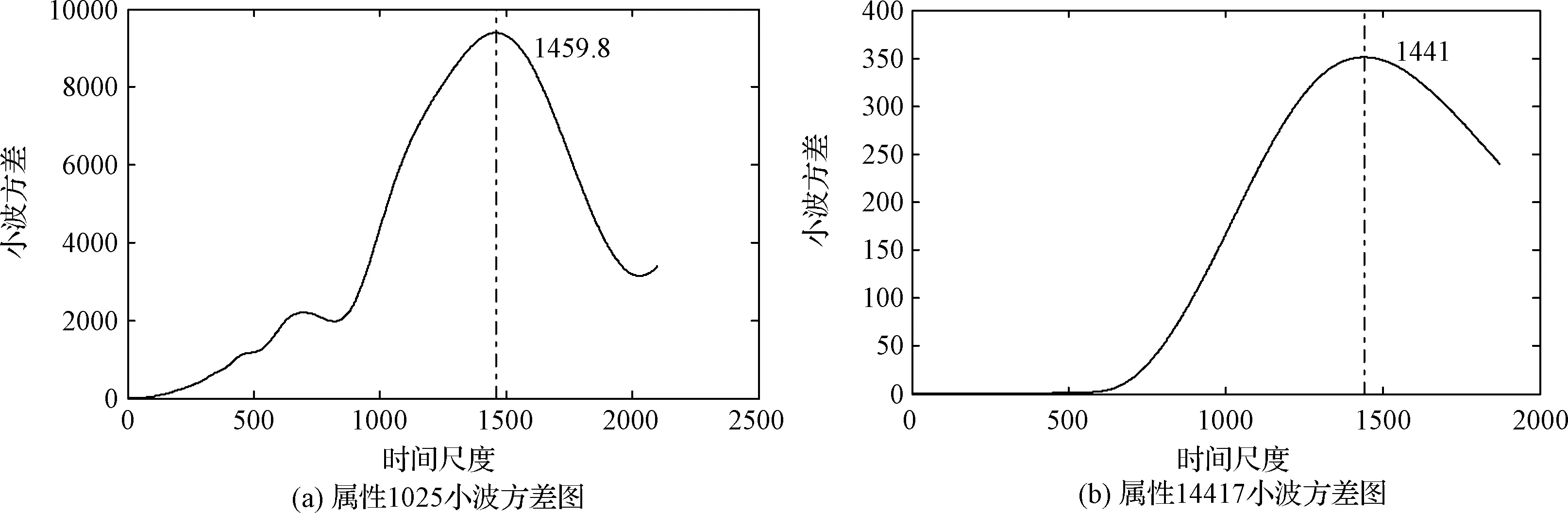
图3 周期分析Fig.3 Analysis of period

4.1 数据预处理

使用一维连续小波对存在野值的数据进行去噪，去除原始遥测数据中的噪声数据，小波函数选择db5，小波尺度为8。为方便进行异常检测，将包含76个属性的遥测数据，以1min为单位压缩成132480条均值数据。最后，对均值数据进行归一化处理。

结合卫星遥测数据的特点，本文将滑动窗口的大小设置为遥测数据的周期。采用小波方差法来获取数据周期，小波方差最高值对应的时间即为周期。根据领域专家建议，对筛选出的部分属性进行了周期分析，图3是1025、14417两个属性的小波方差图。从图3可以看出，两个属性的周期集中在1440左右，因此，本文将滑动窗口大小设置为1440。

4.2 实验分析

本文通过实验分别对两个时间段内的异常检测算法参数k和s的取值进行讨论。参数讨论使用的评价指标为准确度、精确度、召回率、漏报率、误报率和F-score。

针对2014年7月-9月和2015年7月-9月的遥测数据，k值分别取500、750、1000、1250，s值均取200时，分别采用计算异常阈值和无监督分类器来进行异常检测，结果如表1、2和图4所示。

对于2014年7-9月的遥测数据，随着k值的减小，检测准确度和精确度也随之提高，召回率稍有下降，误报率随之降低，F-score相应升高。通过分析表1，当k=500时，准确度、精确度和F-score达到最高，误报率达到最低，异常检测效果最好。

通过分析表2，对于2015年7-9月的遥测数据也表现出了类似结果，然而稍有不同的是，当k=750时，检测准确度、精确度和F-score达到最高，误报率达到最低，异常检测效果最好，此时再减小k值，异常检测效果并没有提升。

图4(a)为异常检测受试者工作特征曲线(Receiver operating characteristic curve,ROC)，图4(b)为精确度—召回率曲线(Preclsion recall curve,PRC)。从图4(a)可以看出，不同的k值，分类器的分类效果都不错，从图4(b)可以看出，不同的k值，其PRC曲线稍有不同。当k=500时，ROC曲线下方覆盖的面积最大，同时其PRC曲线下方覆盖的面积也最大，异常检测效果最好；随着k的增大，ROC曲线下方的面积随之减小。因此，综合分析阈值判别和分类器分类两种方法，本文选择k=500作为2014年7-9月异常检测算法参数。2015年7-9月异常检测ROC和PRC曲线与2014年结果相似。

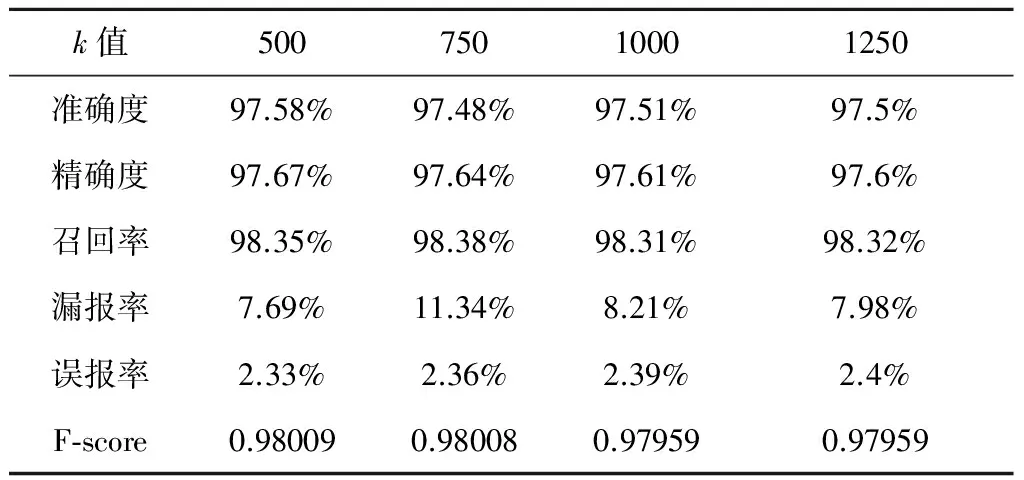
表1 不同k值异常阈值检测结果(2014年)Table 1 Results based on threshold with different k values (2014)

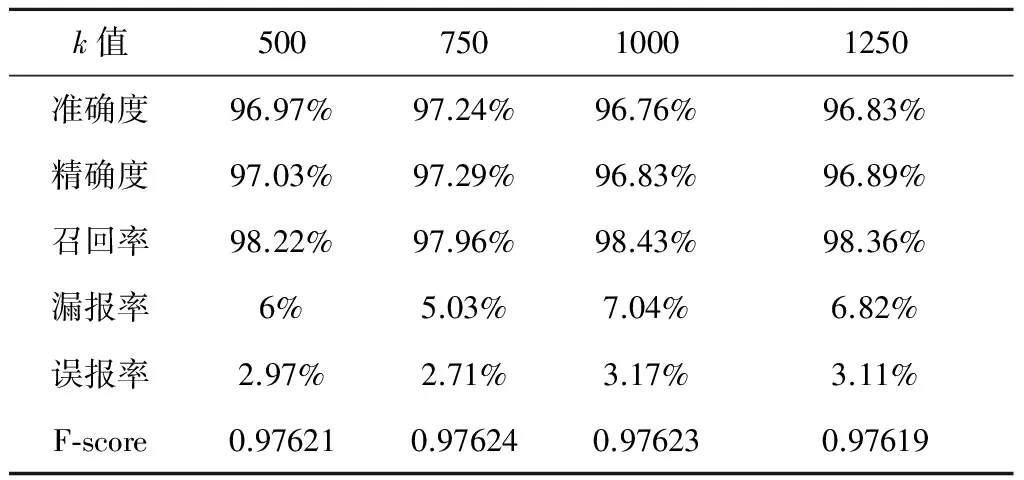
表2 不同k值异常阈值检测结果(2015年)Table 2 Results based on threshold with different k values (2015)

在构建相关数据集空间阶段，本文首先使用K近邻算法筛选K近邻数据集，其中k针对两年的数据分别取500和750，然后采用SNN算法构建共享最近邻子空间，s分别取50、100、150、200、250，分别采用计算异常阈值和分类器进行异常检测，结果如表3～4和图5所示。

对于2014年7-9月的卫星遥测数据，随着s的增大，检测准确度和精确度也随之提高，召回率稍有下降，误报率随之降低，F-score相应升高。通过分析表3，当s=250时，准确度、精确度和F-score达到最高，误报率达到最低，异常检测效果最好。

通过分析表4，对于2015年7-9月的卫星遥测数据也表现出了类似的结果，当s=250时，检测准确度、精确度和F-score达到最高，误报率达到最低，异常检测效果最好。

从图5(a)可以看出，不同的s值，分类器得到的ROC曲线差别不大。然而，从图5(b)可以看出，当k=500，s=50时，PRC曲线明显低于其他曲线，分类器效果最差。随着s的增大，ROC曲线下方的面积随之增大。当s=250时，ROC曲线下方覆盖的面积最大，同时其PRC曲线下方覆盖的面积也最大，异常检测效果最好。综合分析，本文选择s=250作为2014年7-9月异常检测算法参数。

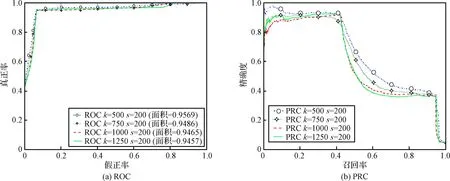
图4 不同k值分类器分类结果(2014年)Fig.4 Classification results with different k values (2014)

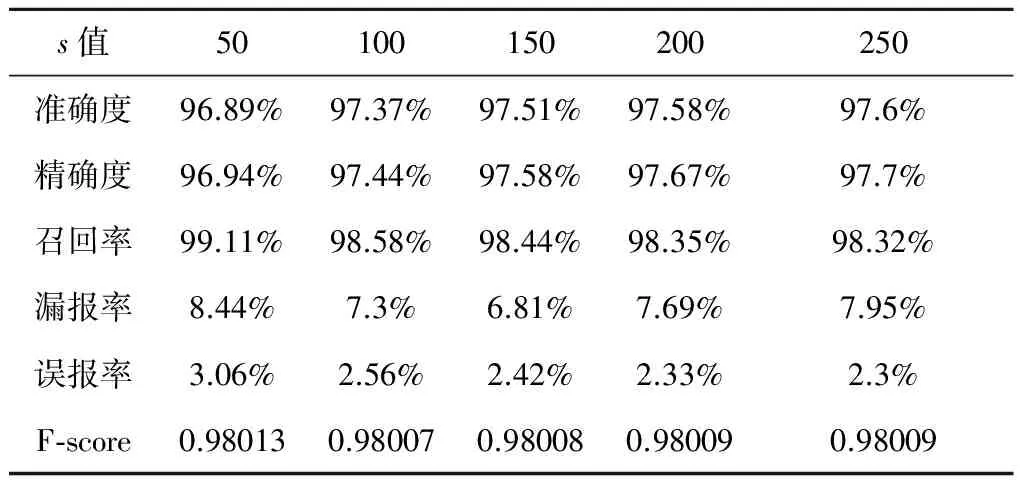
s值50100150200250准确度96．89%97．37%97．51%97．58%97．6%精确度96．94%97．44%97．58%97．67%97．7%召回率99．11%98．58%98．44%98．35%98．32%漏报率8．44%7．3%6．81%7．69%7．95%误报率3．06%2．56%2．42%2．33%2．3%F⁃score0．980130．980070．980080．980090．98009

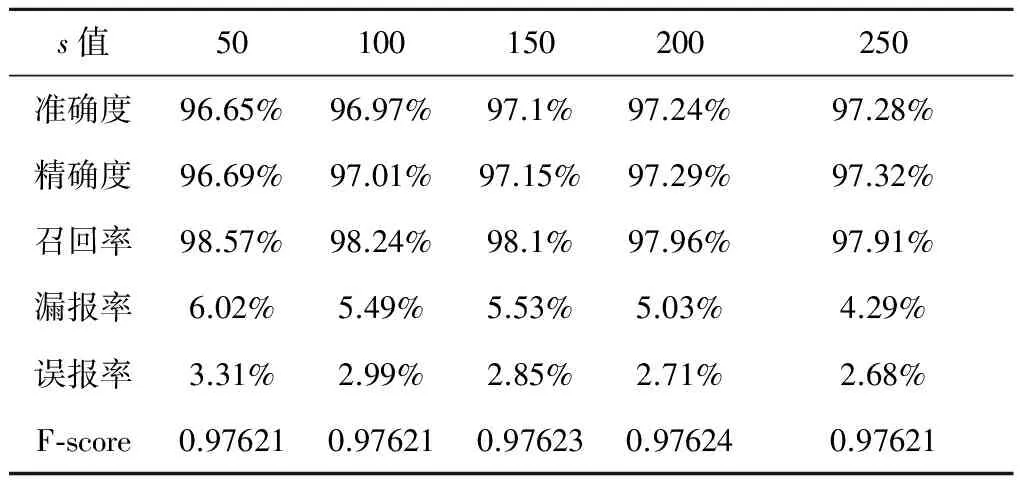
表4 不同s值异常阈值检测结果(2015年)Table 4 Results based on threshold with different s values (2015)

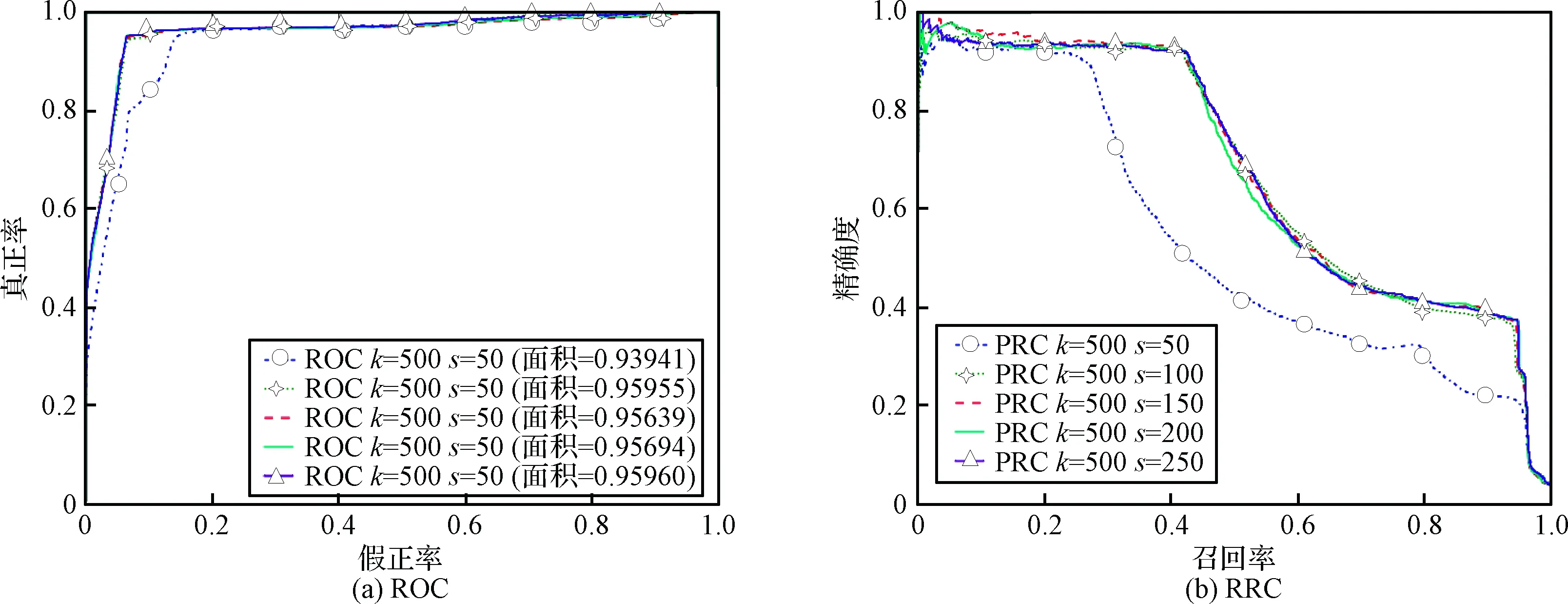
图5 不同s值分类器分类结果(2014年)Fig.5 Classification results with different s values (2014)

为对比本文提出的特征属性筛选算法的优越性，分别采用领域专家筛选的特征属性以及采用灰关联分析选择的属性，与本文提出的基于角度偏离的特征属性选择算法进行对比。灰关联属性选择算法的基本思想是，计算不同属性之间的灰关联度，将灰关联度最小的两个属性放入被选择属性集合，计算剩余的属性与被选择属性集合中属性之间的灰关联度之和，将和最小的属性放入被选择属性集合；重复上述步骤，直到剩余的属性之间的灰关联度大于0.8。该方法将原始的76个属性经过上述方法降维得到以下22个属性，表5中的每一项是每一类属性的一个代表。表6为领域专家筛选出的特征属性。

对比表5、表6发现，灰关联属性选择算法筛选的属性与专家筛选的属性有部分重复，这说明灰关联属性选择算法有一定的可行性，但是筛选属性的数量大约占原始属性的四分之一，由此看出该算法效果一般，仍然保留了许多与异常无关的冗余属性。

表5 灰关联选择属性算法筛选的属性Table 5 Attribute selected by grey relational analysis

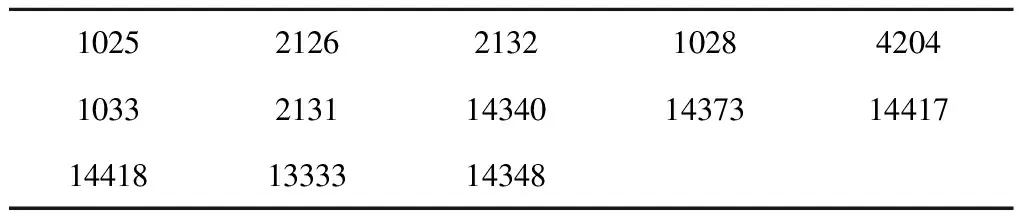
表6 领域专家筛选的属性Table 6 Attribute selected by experts

从表7～8可以看出，在进行异常检测时，由于筛选的属性个数过多，维度高，算法运行时间较长，效率低；本文提出的基于角度偏离的属性选择算法的运行时间多于领域专家属性选择算法，这是因为领域专家给出的属性属于其工作领域的先验知识，是工作经验的积累，不需要消耗计算机的运行时间。

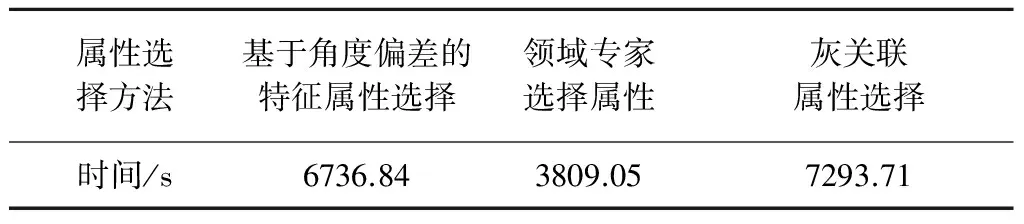
表7 使用三种属性选择算法的异常检测算法的运行时间对比(2014年)Table 7 Comparison of runtime among three attribute selection methods (2014)

表8 使用三种属性选择算法的异常检测算法的运行时间对比(2015年)Table 8 Comparison of runtime among three attribute selection methods (2015)

通过分析表9～10，对于相同的数据集，本文提出的基于角度偏离的特征属性选择方法效果最好，具有最高的准确度、精确度、召回率和F-score，同时，其漏报率和误报率最低，异常检测效果最好。灰关联属性选择算法和领域专家选择属性效果略差于本文提出的属性选择算法。虽然，本文提出的属性选择算法消耗了一定的运行时间，但是异常检测效果要优于其他两种算法，更为重要的是，不需要先验知识。

从图6(a)可以看出，本文提出的基于角度偏离的属性选择算法的ROC曲线明显高于领域专家选择属性的ROC曲线，虽然灰关联属性选择算法的ROC曲线与基于角度偏差的属性选择算法的ROC曲线相差不大，但是从图6(b)可以看出，基于角度偏离的属性选择算法的PRC曲线明显高于灰关联选择属性算法的PRC曲线。因此，综合分析：虽然基于角度偏离的属性选择算法会消耗一定的运行时间，但是在提高检测效果的前提下，必要的消耗是值得的。

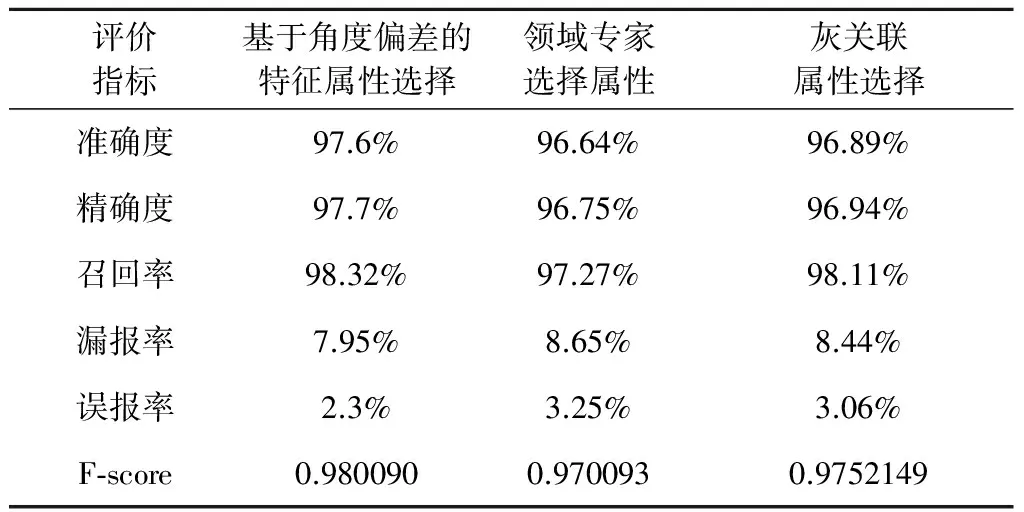
表9 不同属性选择算法异常阈值检测结果(2014年)Table 9 Results based on threshold with three attribute selection methods (2014)

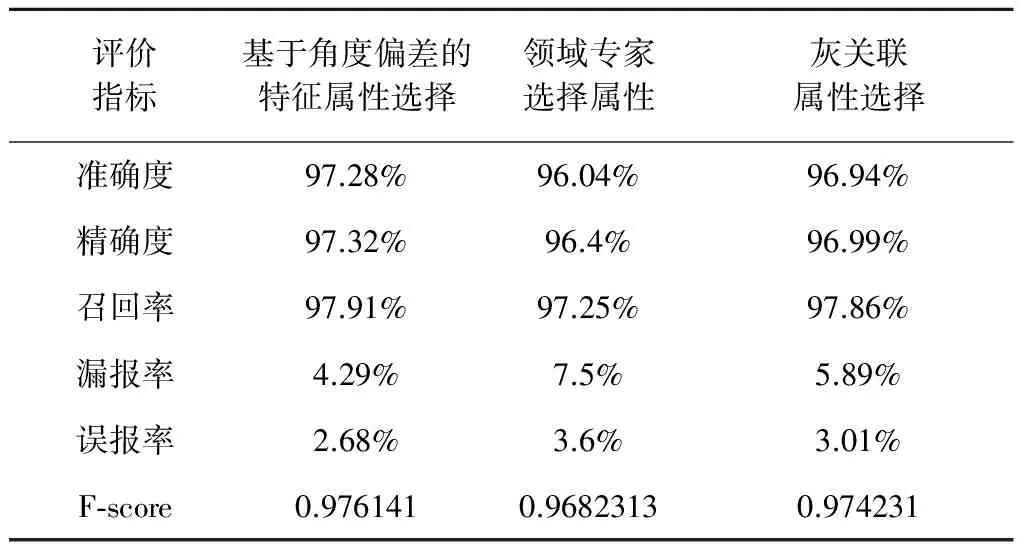
表10 不同属性选择算法异常阈值检测结果(2015年)Table 10 Results based on threshold with three attribute selection methods (2015)

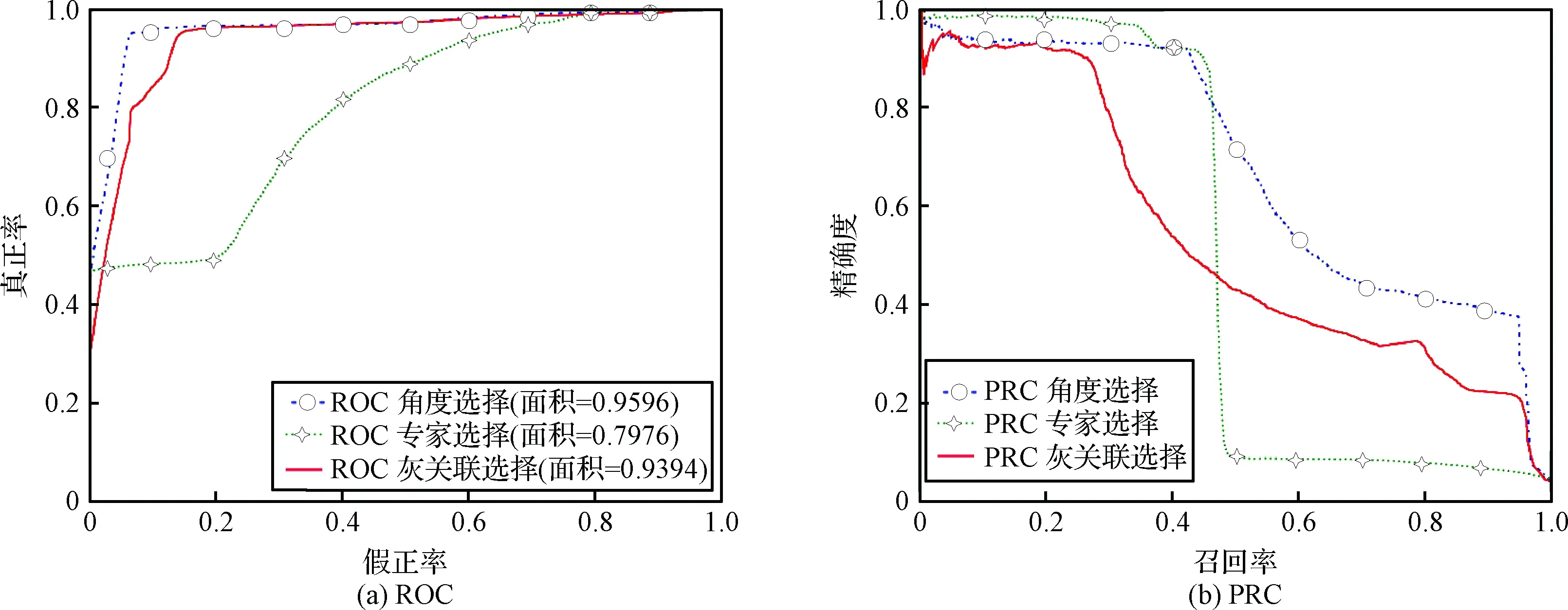
图6 不同属性选择算法分类器分类结果(2014年)Fig.6 Classification results with three attribute selection methods (2014)

为验证本文提出算法的可靠性，将本文提出的算法(ADMAD)与同领域相关学者，如Zhang等[10]提出的基于角度的高维数据子空间异常检测算法(ABSAD)、Sarah等[11]提出的基于深度信念网络的无监督高维异常检测算法(Deep belief network,DBN)、传统的基于主成分分析的异常检测算法(Principal component analysis,PCA)和改进的基于角度方差的异常检测算法(Fast angle-based outlier detection,fastABOD)进行对比，对比结果如图7和表11～12所示。从图7可以看出，本文提出的ADMAD算法在两个数据集上都具有较高的准确率，在处理异常数据与正常数据不平衡问题时性能稳定，而ABSAD算法在两个数据集上得到的结果差别较大，说明该算法性能不稳定、鲁棒性较差。DBN算法和PCA算法在处理异常数据与正常数据不平衡问题时，异常检测的效果不好，从PRC曲线看出，这两种方法的预测结果与真实结果偏离较大。

fastABOD算法的检测准确率最低，从ROC曲线和PRC曲线均可看出，fastABOD算法得到的曲线所包围的面积最小，异常检测效果最差。

表11 不同异常检测算法的运行时间对比(2014年)Table 11 Comparison of runtime among different anomaly detection methods (2014)

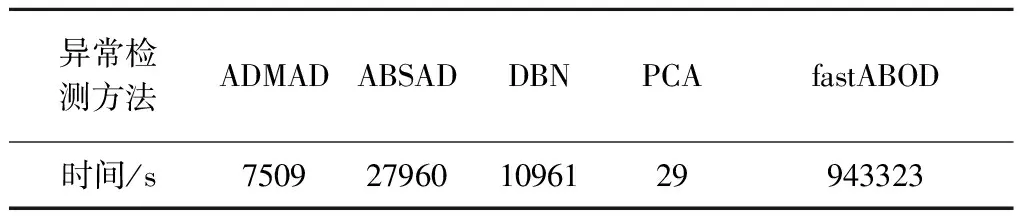
表12 不同异常检测算法的运行时间对比(2015年)Table 12 Comparison of runtime among different anomaly detection methods (2015)

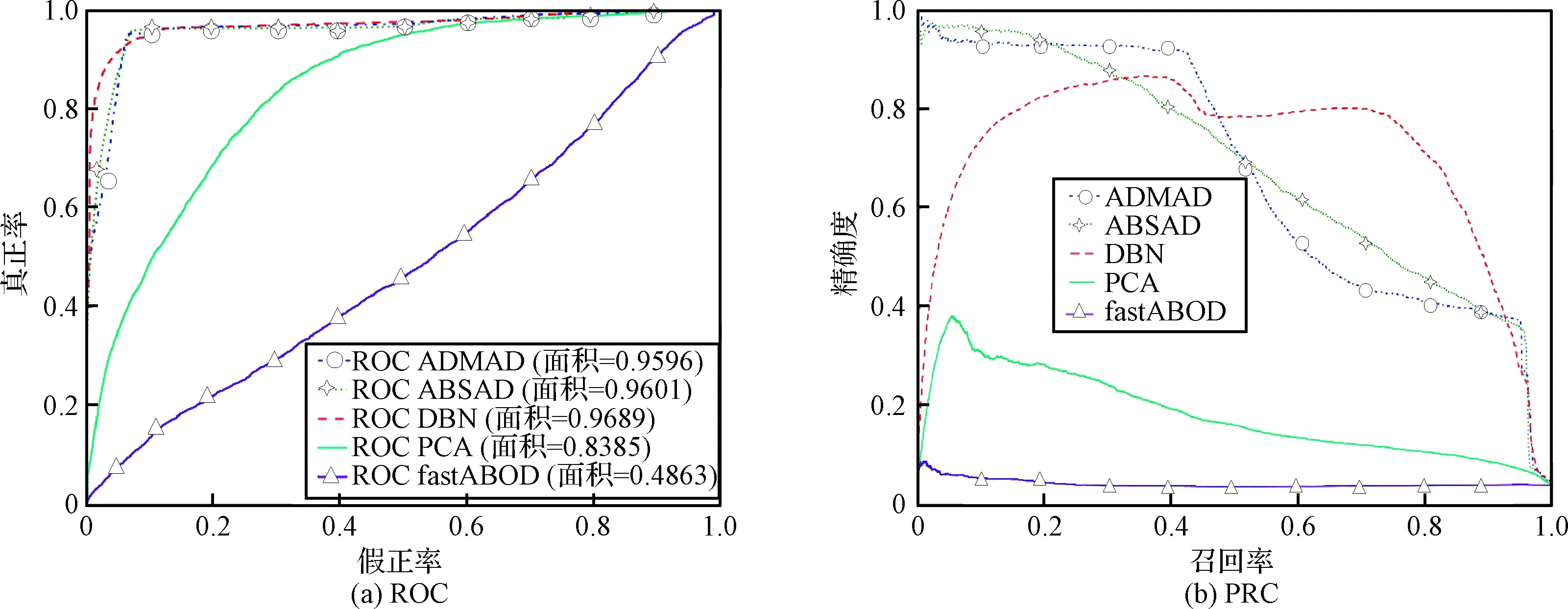
图7 不同异常检测算法结果对比(2014年)Fig.7 Comparison among different anomaly detection methods (2014)

由表11～12可知，fastABOD算法的运行时间最长，其次是ABSAD算法，DBN算法的运行时间略长于ADMAD算法，PCA算法的运行时间最短。虽然PCA算法的运行时间最短，但是对于卫星较常出现的局部异常该算法并不适用。DBN在构建深度信念网络结构时消耗的学习时间较长。fastABOD算法时间复杂度为O(dn2+dnk2)，ABSAD算法时间复杂度为O(n2·max(d,k))，这两种算法复杂度过高，在数据量较大时难以做到实时检测。本文提出的算法时间复杂度为O(n(m·max(k,d)+k))，大大降低了算法运行时间，提高了算法效率，能够满足卫星异常实时检测的需要。

5 结 论

针对卫星遥测数据量大，维度高，异常数据难以发现的问题，提出一种基于角度偏差的异常检测算法。采用角度替换距离的思想，将基于距离度量的异常检测算法修改为基于角度度量的异常检测算法。同时，引入滑动窗口机制，缩小了搜索空间，降低了算法运行时间；采用共享近邻算法进一步缩小搜索空间，使用基于角度偏离的属性选择算法筛选特征属性，并结合归一化的马氏距离计算数据记录的异常值。在不需要领域知识的前提下，该方法通过统计学知识计算异常阈值判断数据记录是否为异常数据记录，异常检测的准确度较高，其检测结果得到了领域专家的认可，同时，本文提出的算法可以推广到其他卫星或航天器的异常检测中。因此，在领域专家知识匮乏的情况下，本文提出算法能够满足卫星健康监测的异常检测需要。

[1] 顾胜, 魏蛟龙, 皮德常. 一种粒子群模糊支持向量机的航天器参量预测方法[J]. 宇航学报, 2014, 35(11): 1270-1276. [Gu Sheng, Wei Jiao-long, Pi De-chang. Particle swarm optimization-fuzzy support vector machine based prediction of spacecraft parameters[J]. Journal of Astronautics, 2014, 35(11):1270-1276.]

[2] 代成龙, 皮德常, 方针，等. 半球谐振陀螺仪寿命的一种长周期预测方法[J]. 宇航学报, 2015, 36(1): 109-116. [Dai Cheng-long, Pi De-chang, Fang Zhen, et al. A long-term lifetime prediction method for hemispherical resonator gyroscope[J]. Journal of Astronautics, 2015, 36(1):109-116.]

[3] Krogel P. Outlier detection techniques[C]. The 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, July 25-28, 2010.

[4] Kriegel H P, S Hubert M, Zimek A. Angle-based outlier detection in high-dimensional data[C]. The 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, Nevada, USA, August 24-27, 2008.

[5] Pham N, Pagh R. A near-linear time approximation algorithm for angle-based outlier detection in high-dimensional data[C]. The 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, August 12-16, 2012.

[6] Ye H, Kitagawa H, Xiao J. Continuous angle-based outlier detection on high-dimensional data streams[C]. The 19th International Database Engineering & Applications Symposium, Yokohoma, Japan, July 13-15, 2015.

[7] Cover T M, Hart P E. Nearest neighbor pattern classification [J]. IEEE Transactions on Information Theory, 1967, 13(1): 21-27.

[8] Keller J M, Gray M R, Givens J A. A fuzzy K-nearest neighbor algorithm[J]. IEEE Transactions on Systems Man & Cybernetics, 1985, SMC-15(4):580-585.

[9] Jarvis R A, Patrick E A. Clustering using a similarity measure based on shared near neighbors[J]. Computers IEEE Transactions on, 1973, C-22(11): 1025-1034.

[10] Zhang L, Lin J, Karim R. An angle-based subspace anomaly detection approach to high-dimensional data: with an application to industrial fault detection[J]. Reliability Engineering & System Safety, 2015, 142(10): 482-497.

[11] Erfani S M, Rajasegarar S, Karunasekera S, et al. High-dimensional and large-scale anomaly detection using a linear one-class SVM with deep learning[J]. Pattern Recognition, 2016, 58(10): 121-134.

通信地址：江苏省南京市江宁区将军大道29号南京航空航天大学计算机科学与技术学院(211106)

E-mail：kx2014vip@163.com

皮德常(1971-)，男，博士，教授，主要从事数据挖掘、大数据处理方向研究。本文通信作者。

通信地址：江苏省南京市江宁区将军大道29号南京航空航天大学计算机科学与技术学院(211106)

E-mail：dc.pi@nuaa.edu.cn

An Anomaly Detection Method Based on Angle Deviation for Satellite Subsystem

KANG Xu1, PI De-chang1, TIAN Hua-dong2

(1. College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China;2. System Design Department of China Academy of Space Technology, Beijing 100094, China)

In order to ensure the stable operation of a satellite and prolong its life, an anomaly detection method based on angle deviation(ADMAD) is proposed. In the high-dimensional data space of the satellite telemetry data, the method applies the shared nearest neighbors (SNN) algorithm to construct the reference point sets. Then the method selects the feature attributes associated with the anomaly by applying a method based on angle deviation using angle replacing distance.Finally, the normalized Mahalanobis distance is used to calculate the anomaly scores of points. Combining with the statistical knowledge, the threshold based on the anomaly scores is obtained, and the data sets are classified. We verified the proposed method using the telemetry data in control and power subsystem of a satellite in July to September, 2014 and July to September, 2015 respectively. The experimental results indicate that the accuracy of the proposed algorithm could reach more than 95% under the condition of lack of the field knowledge.The robustness of the proposed algorithm is higher. Simultaneously, it can detect the anomaly of satellite subsystem timely and effectively.

Satellite subsystem; Angle deviation; Attribute selection; Anomaly detection

2017-01-05;

2017-04-23

国家自然科学基金(U1433116);研究生创新基金(实验室)开放基金(Kfjj20161604)

V241.5+54

A

1000-1328(2017)06-0638-09

10.3873/j.issn.1000-1328.2017.06.011

康 旭(1993-)，女，博士生，主要从事数据挖掘方向研究。