火箭推进剂加注系统流量计系数的现场标定
任永平,凌 斌,崔本廷,崔 燕
(1. 太原卫星发射中心,太原030027;2. 太原理工大学,太原030027)
火箭推进剂加注系统流量计系数的现场标定
任永平1,凌 斌1,崔本廷1,崔 燕2
(1. 太原卫星发射中心,太原030027;2. 太原理工大学,太原030027)
针对液体火箭推进剂加注系统计量精度差的问题,提出一种拆分―重组的测量数据处理方法。该方法将流量计的现场测量数据拆分成若干分量的凸组合形式,再将各分量重组以构成有效的最小二乘算式,同时引入遗忘因子对测量数据的时效性进行折衷;分别按照两种常见的工程情况,利用发射任务实测数据检验了方法的有效性和实用性。这一方法解决了流量系数的现场标定问题,提高了加注系统的计量精度。
推进剂加注;流量系数;隶属函数;最小二乘;参数辨识
0 引 言
推进剂加注对液体火箭的入轨精度乃至发射成败有着至关重要的影响。加注过量或欠量都会导致火箭的动力学模型参数发生变化[1-2],进而影响到它的控制性能和精度,严重时会使发动机关机条件无法满足,从而导致发射失败[3]。
由于在流量系数标定上的缺陷,现有的加注量计量方法精度较差。尽管采用一些修正手段[4]能够提高计量精度和范围,但这种固定形式的流量系数从根本上并不能消除系数漂移所带来的误差,为此,需要采用流量系数现场标定方法,以获取准确的流量系数。而利用在线辨识方法进行流量系数现场标定,无论是经典的多项式拟合[5],还是新近提出的一些智能辨识方法[6-7],都很难根据现场已知条件(测量信号的时间序列及其相应的总输出结果)罗列出有效的参数辨识算式。因此,直接利用现场测量数据进行流量系数现场标定的做法尚未见报道。实际工程中有采用多传感器数据融合[8]来提高加注量计量精度的,但这种做法效果有限。
本文主要讨论如何利用现场测量数据对流量系数进行参数标定,以实现推进剂加注量的精确计量。首先,简要介绍了推进剂加注系统的工艺原理,指出现有计量方法的不足。其次,利用模糊数学中的隶属函数[9-10]概念将流量系数表示成若干离散样本点的凸组合形式,并基于这种凸组合结构,对测量数据进行拆分—重组处理,得到了有效的最小二乘算式。由于测量数据在拆分—重组处理时要大量用到累加运算,因此,这一处理方法能有效滤除信号中的噪声。最后,以发射任务的实测数据检验本文方法的效果,并针对实际工程中可能遇到的测量数据不足、数据观测阵条件数过大[11]等问题展开讨论,提出了相应的解决办法。
1 推进剂加注工艺原理
火箭推进剂加注系统是将液态推进剂由罐车或库房经管路泵入火箭的贮箱,其工艺原理如图1所示。图中的L1是适用于大流量的流量计,而L2是适用于小流量的流量计。在火箭贮箱里分别设立了3个液位触点。在推进剂加注的起始阶段,阀门A开启、B关闭,加注系统以大流量形式工作;当贮箱内的液面达到1液位时,1液位触点接通,贮箱发出“1液位到”信号,阀门A关闭、B开启,加注系统以小流量形式工作;当液面到达2液位时,同样触发“2液位到”信号,加注系统继续以小流量方式工作,直至推进剂液面达到期望液位(由轨道计算确定)。此时,总的推进剂加注量Vtotal为:
Vtotal=V0-1+V1-2+ΔV
式中:V0-1是1液位之前的贮箱容积,V1-2是1液位和2液位之间的贮箱容积,这两个容积值是事先已知的。ΔV是2液位到期望液位之间的容积,这一容积值随发射任务的不同而不同,无法事先确定,只能依靠对流量计的测量数据进行积分得到,而积分必然会涉及到积分误差问题,这就要求流量计系数标定得较为准确,以尽可能地减小积分误差。
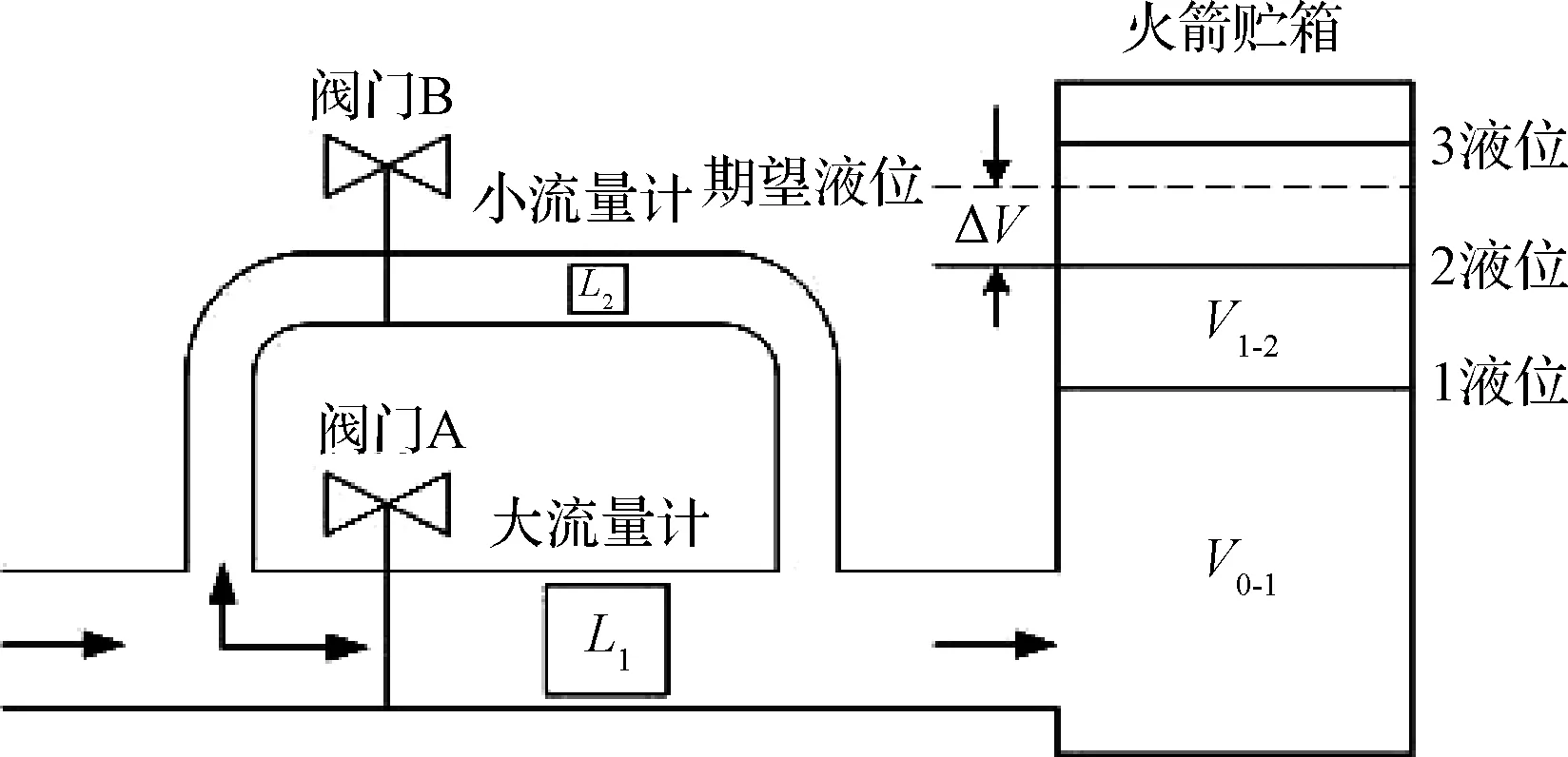
图1 加注系统工艺原理示意图Fig.1 Schematic diagram of rocket propellant filling system
根据涡街流量计[12]的工作原理,管路内的流量q为:

(1)
式中:f为涡街流量计的流速信号(脉冲数/秒),k为流量系数(脉冲数/升)。为了表述方便,本文将流量系数的倒数μ=1/k称为流量系数。
流量系数μ的值一般由厂商提供,它是通过测量流量计在若干个不同流速样本下的流量系数,再按照相关规范[13]的要求,求取一个平均值作为该流量计的流量系数。以图1中的L2流量计为例,厂商提供了如表1形式的数据,其中四个流速样本点设为fi(i=1,…,4),而相应流速样本点处的流量系数设为μi(i=1,…,4)。按照规范,舍弃较少用到的流速f1及系数μ1,取其余三个数的最大值和最小值的平均,作为该流量计的流量系数,对于表1中4组数据,其流量系数的平均值为[13]0.1134。

表1 厂商提供的流量计流速样本点的数据格式Table1 Data example of flowmeter provided by manufacturer
这种做法存在以下不足:
1)由于测试环境、介质条件的不同,厂商提供的流量系数并不一定适合发射场;另外,随着使用时间的增加,流量计难免会产生一些内外部变化,从而导致其流量系数发生漂移。
2)受实验条件的限制,厂商在测试流量计时往往不能做到满量程测试,比如,当厂商用水作为介质进行测试时,水的流速要受到水塔高度的限制,而水塔高度又受到工程造价的限制,因此,许多厂商常常提供不了流量计在较高流速下的流量系数。
3)由表1可知,当介质流速不同时,相应的流量系数也不相同,而上述取平均值的做法则完全忽略这种差异,当实际加注过程中的流速和厂商测试所用的平均流速不相同时,厂商提供的流量系数就不再适用。
2 数据处理的拆分—重组方法
要解决上述问题,需要考虑流量系数随流速而变化的情况,并采用现场标定方法来提高流量系数的准确度。而由前文的加注系统工艺原理介绍可知,流量计数据处理的已知条件仅为:流量计输出的流速信号,以及固定液位处所对应的容积值(如图1中的V0-1和V1-2)。根据这些已知条件很难列出有效的最小二乘式。为此,本文提出一种拆分—重组的数据处理方法,巧妙地解决了上述难题。
首先介绍最小二乘法的一个性质。考虑如下最小二乘式:
V=ΦU+N
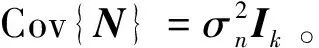
性质1[14].令系统的输出残差为:ε=V-ΦU,则有:
(2)
式中:E{·}表示数学期望。
性质1表明,在随机噪声N和试验次数k相同的情况下,增加待估计变量的个数m能减小输出残差ε(即容积计算误差)的期望值。其物理意义是:较少数量的待估计变量不足以兼容不同试验数据之间的差异。
假设流量计的实际流速为Fj(j=1,…,n),这里,为了和选定的样本点流速相区别,实际流速用大写的Fj(j=1,…,n)来表示,而样本点流速则用小写的fi(i=1,…,4)来表示。实际流速的累积脉冲数∑Fj所对应的容积值v为已知量。由式(1)可知:
(3)
由性质1可知,如果流量系数μ采用平均值形式,则待估计变量的个数m=1,利用现场数据对系数μ进行辨识,其输出残差会比较大。另外,考虑到流量系数实际上是流速的函数,可以将式(3)中的流量系数μ表示成如下函数形式:

(4)
式中:参数λi(Fj)(i=1,…,m)称为隶属函数,是已知量;而μi(i=1,…,m)为待估计的未知量。将式(4)代替式(3)中的系数μ,就可以增加待估计变量的个数,减小计算误差;同时也能将流量系数表示成随流速而变化的函数形式。
增加待估计变量个数的缺点是需要更多的试验数据来支持(k>m)。因此,待估计变量个数的一个合理的工程选择是,在厂商提供的数据基础上再增加1个待估计量,使流量计的流速能够覆盖工程所需,以弥补厂商提供不了大流速时的流量系数的缺陷。结合表1,式(4)的工程实现为:

(5)
式中:μ1,…,μ4为厂商提供的样本点处的流量系数,而μ5为人为引入的未知量,它和实际加注过程中的最大流速fmax相对应。
式(5)中的隶属函数λi(Fj)(i=1,…,5)可以用如下的距离约束予以确定:
(6)
式中:fi(i=1,…,5)为样本点处的流速,参数m表示距离约束的程度,当m=1时即为三角形隶属函数[9]。
将式(5)~(6)代入式(3),得:
(7)
式(7)即为标准的最小二乘算式,式中参数σi(i=1,…,5)的物理意义是和容积v所对应的总脉冲数∑Fj中,与某一样本点fi(i=1,…,5)相对应的脉冲数总分量为:
(8)
式(7)所对应的数据处理过程如图2所示。图中,每一时刻的Fj按照隶属函数λi(Fj)(i=1,…,5)拆分为各个样本点fi(i=1,…,5)所对应的分量,最后将这些分量各自相加,重组成总脉冲数∑Fj在各样本点fi(i=1,…,5)处的总分量,乘以相应的系数μi(i=1,…,5)后即为式(7)。
通过拆分—重组的处理,流量计测试信号中的特征被分解得更为细致;另外,由于重组是个累加过程,测量信号Fj(j=1,…,n)中的噪声也将被过滤掉,有利于提高数据辨识的精度。
测量数据的试验时间一般不同,这时,可以考虑根据测量数据的“新鲜程度”,在式(7)中引入如下的遗忘因子ηi[15]:
ηi=α(i-1)-β, 0<α≤1
(9)
式中:参数α表示遗忘率;参数i表示试验排序,i=1表示最近的一次液位数据,而i=p表示同一火箭最早的液位数据;参数β用来区分不同火箭。参数α、β的具体取值不会对辨识结果造成显著差异,因而可以根据实际工程情况人为选定。
为叙述和应用的方便,下面完整列出流量计数据处理所用到的最小二乘式:
(10)
式(10)可简化为:
ΦU=V
(11)
式中:Φ为数据观测阵,列向量U为待估计变量,V为液位容积值。
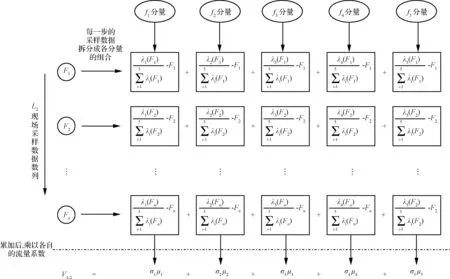
图2 测量数据的拆分—重组处理过程Fig.2 Procedure of split and recombination for the measured data
3 实际加注数据的处理
本节利用实际加注数据检验上述方法。有两种情形在实际工程中是最常遇到的:一是数据量不足,二是数据阵的条件数过大,下面结合实测数据,详细讨论这两种情况下数据处理的方法和步骤。
3.1 数据量不足时的处理
根据图3的实测数据,将流量计L2的最大流速限定为fmax=100(脉冲数/秒)。按照图2的拆分—重组处理过程,可以求得总脉冲数∑Fj在各样本点处的分量σi(i=1,…,5),其结果如表2所示。
由于数据个数只有4个,利用式(10)不能求出全部5个参数μi(i=1,…,5),这时,可以考虑将前4个系数μi(i=1,…,4)直接取为厂商提供的数据,而只求解未知参数μ5。由于4个数据是同一火箭的,遗忘因子(式(9))中的参数可以考虑选择为:β=0,α=0.95。将表2数据、遗忘因子ηi以及贮箱不同液位间的标称容积值(如表3中的标称值)代入式(10),求解该最小二乘式可得μ5=0.1174。
得到各样本点处的参数(fi,μi)(i=1,…,5)的值以后,就可以按照式(6)计算每个采样数据Fj(j=1,…,n)的隶属度,进而利用式(5)求得Fj所对应的流量系数,两者相乘为流量,累加后得到加注量。其计算结果和传统的、流量系数取固定值的计算结果的比较见表3。从表3中的方差计算结果可以看出,本文方法比传统方法精度要好很多。
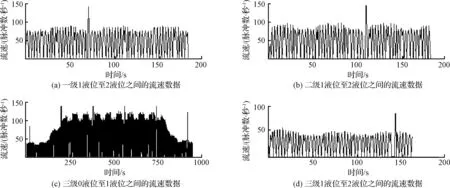
图3 火箭A加注系统的原始测量数据Fig. 3 Original measurement data collected from propellant filling system of the rocket A
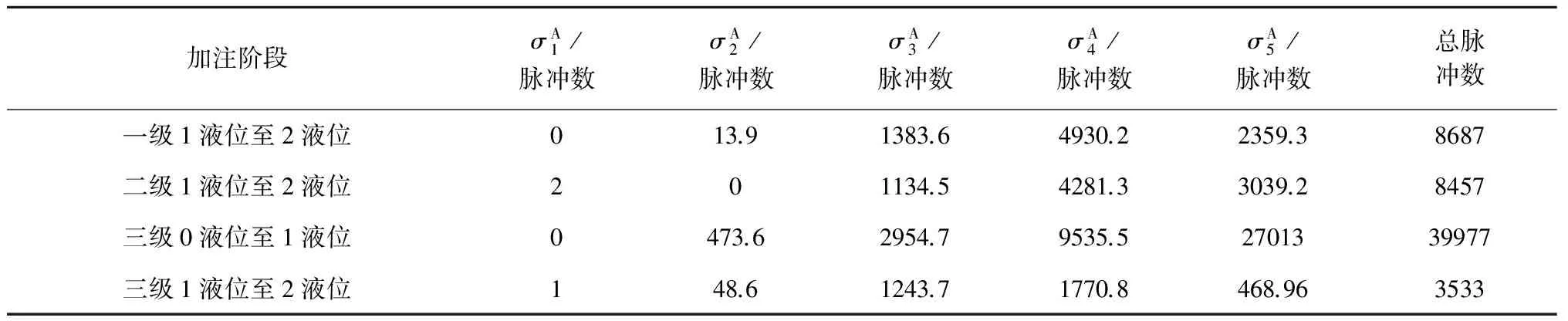
加注阶段σA1/脉冲数σA2/脉冲数σA3/脉冲数σA4/脉冲数σA5/脉冲数总脉冲数一级1液位至2液位013.91383.64930.22359.38687二级1液位至2液位201134.54281.33039.28457三级0液位至1液位0473.62954.79535.52701339977三级1液位至2液位148.61243.71770.8468.963533

表3 第3.1节方法和传统方法加注量计算结果的比较Table 3 Comparison of the calculation results of the method in section 3.1 and the traditional method
3.2 数据观测阵条件数过大时的处理
如果有更多的数据源,则可以利用式(10)求解全部5个样本点处的系数值,但这时需要注意数据观测阵条件数过大而引发的辨识精度问题[11]。
假设另外一发火箭B的推进剂加注数据经处理后,得到如表4所示的各样本点处的脉冲数分量。遗忘因子(式(9))中参数选为:α=0.95、β=0.3。将火箭A、B的各个总脉冲数分量(表2、表4数据)以及贮箱不同液位间的容积值代入式(10),求解该最小二乘式可得:
和厂商提供的参数相比,μ1=1.5348和μ2=0.1649明显过大,是不合理的。造成这一错误的原因是数据阵Φ第一列和第二列的数值太小,使得数据阵Φ的条件数过大,从而导致计算误差太大。
为解决这一问题,可以将参数μ1、μ2直接设定为厂商提供的数值,将其代入式(10),只求解μ3、μ4、μ5的值。最后求得μi(i=1,…,5)的值为:
和厂商提供的数据相比,这个结果非常合理,从数值上看,是完全可以接受的。
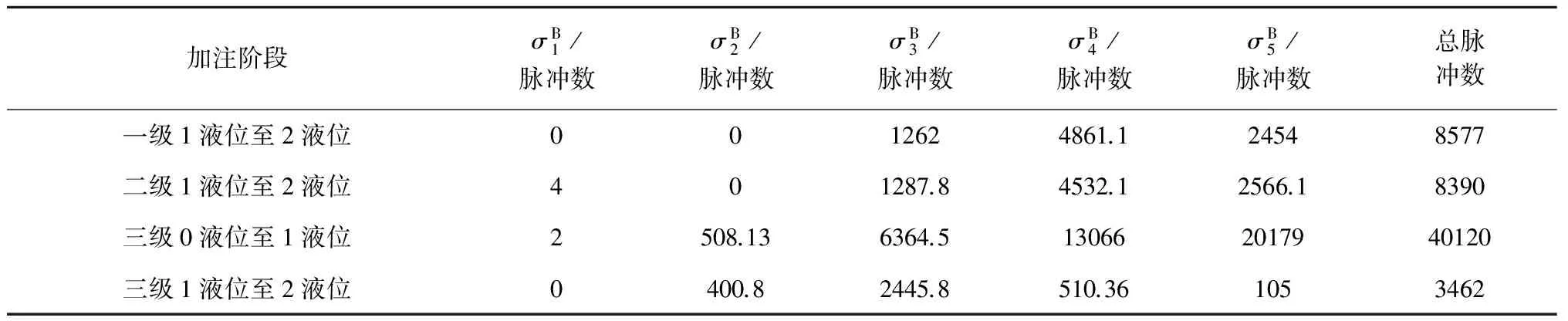
表4 火箭B的总脉冲数在各样本点处的分量Table 4 Components at discrete data points among total pulse number of the rocket B

表5 第3.2节方法和传统方法加注量计算结果的比较Table 5 Comparison of the calculation results of the method in section 3.2 and the traditional method
利用得到的μi(i=1,…,5)系数值可以同时计算火箭A、B贮箱不同液位间的加注量,其结果如表5所示。从表5可以看出,这组参数μi(i=1,…,5)能够较为准确地同时计算出火箭A、B的加注量。
综合上述两种情况来看,采用本文提出的方法能够使加注量的计量精度提高200多倍(按方差来衡量),足以证明本文方法的优势。
4 结 论
针对传统推进剂加注量计量方法存在的缺陷,提出一种测量数据拆分—重组的处理方法,巧妙地解决了加注系统流量系数现场标定所遇到的难于罗列辨识算式的难题。数据拆分是将一个测量数据表示成若干离散样本点处数据的凸组合形式,从而使待估计变量的个数增加,输出残差减小,同时也能将流量系数表示成流速的函数形式,更符合流量计的计量特性;数据重组则是将各样本点处的数据分量进行累加,和总的过程输出结果构成有效的最小二乘算式,数据重组的累加操作有利于抑制测量数据中的噪声。实例分析计算表明,利用拆分—重组的处理方法能非常准确地标定流量系数,大大提高了推进剂加注量的计量精度。
本文所解决的问题不仅是流量计标定时遇到的问题,它也是一个常见的工程问题——即已知测试信号序列及该信号所对应的结果,辨识出相应的系统参数,采用拆分—重组的数据处理方法能有效解决这类辨识问题。
[1] 邓明乐, 岳宝增, 黄华. 液体大幅晃动类等效力学模型研究[J]. 宇航学报, 2016, 37(6):631-638. [Deng Ming-le, Yue Bao-zeng, Huang Hua. Study on the equivalent mechanical model for large amplitude slosh[J]. Journal of Astronautics, 2016, 37(6):631- 638.]
[2] 李青, 马兴瑞, 王天舒. 非轴对称贮箱液体晃动的等效力学模型[J]. 宇航学报, 2011, 32(2):242-249. [Li Qing, Ma Xing-rui, Wang Tian-shu. Equivalent mechanical model for liquid sloshing in non-axisymmetric tanks [J]. Journal of Astronautics, 2011, 32(2):242-249.]
[3] 丁文华. 近年运载火箭发射失败原因分析[J]. 国际太空, 2009, 8:14-19. [Ding Wen-hua. Analysis on the failure of launch vehicle launch in recent years[J]. Space International, 2009, 8:14-19.]
[4] 叶佳敏, 张涛. 浮子流量传感器线性度的研究[J]. 传感技术学报, 2007, 20(3):570-574. [Ye Jia-min, Zhang Tao. Study on the linearity of float flow sensors[J]. Chinese Journal of Sensors and Actuators, 2007, 20(3):570-574.]
[5] 董云龙, 何友, 王国宏, 等. 一种改进的系统偏差估计算法[J]. 宇航学报, 2005, 26(6):737-742. [Dong Yun-long, He You, Wang Guo-hong, et al. One modified algorithms to estimate system errors[J]. Journal of Astronautics, 2005, 26(6):737-742.]
[6] 董帅, 徐科军, 侯其立, 等. 微弯型科氏质量流量计测量气-液两相流研究[J]. 仪器仪表学报, 2015, 36(9):1972-1977. [Dong Shuai, Xu Ke-jun, Hou Qi-li, et al. Study on measuring gas-liquid two-phase flow with microbend type Coriolis mass flowmeter[J]. Chinese Journal of Scientific Instrument, 2015, 36(9):1972- 1977.]
[7] 吴瑕, 周焰. 模糊传感器与区间型多属性决策的信息融合方法[J]. 宇航学报, 2011, 32(6):1409-1415. [Wu Xia, Zhou Yan. Method of information fusion based on fuzzy sensor and interval multi-attribute decision-making [J]. Journal of Astronautics, 2011, 32(6):1409-1415.]
[8] 王新峰, 王洪志, 高敏忠. 基于累积误差效应的瞬变加注量融合算法[J]. 北京航空航天大学学报, 2012, 38(5):670-674. [Wang Xin-feng, Wang Hong-zhi, Gao Min-zhong. Fusion algorithm for transient loading volume with accumulative error [J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(5):670-674.]
[9] 黄卫华, 方康玲, 章政. 典型模糊控制器的隶属函数设计及分析[J]. 模糊系统与数学, 2010, 24(5):83-90. [Huang Wei-hua, Fang Kang-lin, Zhang Zheng. Analysis and design of membership function for a typical fuzzy controller [J]. Fuzzy System and Mathematics, 2010, 24(5):83-90.]
[10] 董炜, 陈卫征, 徐晓滨, 等. 基于可分性测度的模糊隶属函数确定方法[J]. 控制与决策, 2014(11): 2089-2093. [Dong Wei, Chen Wei-zheng, Xu Xiao- bin, et al. Determination method of fuzzy membership function based on separability measure[J]. Control and Decision, 2014(11): 2089-2093.]
[11] 周浩. 线性数据拟合方法的误差分析及其改进应用[J]. 大学数学, 2013, 29(1):70-76. [Zhou Hao. Error analysis and improved application of linear data fitting method [J]. College Mathematics, 2013, 29(1):70-76.]
[12] 郑德智, 王帅, 樊尚春. 涡街流量传感器信号处理方法研究[J]. 传感技术学报, 2009, 22(1):80-84. [Zheng De-zhi, Wang Shuai, Fan Shang-chun. Research on signal processing method of vortex flowmeter[J]. Chinese Journal of Sensors and Actuators, 2009, 22(1):80-84.]
[13] JJG 1037-2008, 涡轮流量计检定规程[S].
[14] 邬吉波. 线性模型参数估计的若干性质研究[D]. 重庆:重庆大学, 2013. [Wu Ji-bo. Research on the properties of parameter estimation in linear regression model [D]. Chongqing: Chongqing University, 2013.]
[15] 刘学彦, 王昕, 王振雷. 带遗忘因子的线性回归性能评估算法及应用[J]. 控制工程, 2014, 21(6):867- 872. [Liu Xue-yan, Wang Xin, Wang Zhen-lei. Performance assessment algorithm of improved linear regression with forgetting factor (ILR) and its application [J]. Control Engineering of China, 2014, 21(6): 867-872.]
通信地址:山西省太原市200信箱8号(030027)
电话:(010)6015290
E-mail:waterman4633@sina.com
Field Calibration of Flowmeter Coefficient of Rocket Propellant Filling System
REN Yong-ping1, LING Bin1, CUI Ben-ting1, CUI Yan2
(1. Taiyuan Satellite Launch Center, Taiyuan 030027, China; 2. Taiyuan University of Technology, Taiyuan 030027, China)
In order to solve the problem of the poor measurement precision of a liquid rocket propellant filling system, a new data processing method called split and recombination is presented. The method splits the measured data into some components which are in the form of convex combination, and then recombines those components respectively to constitute a valid least squares equation. At the same time, a forgetting factor is employed to compromise the time-effectiveness of the measured data. The validity and practicability of this method are verified by the actual measured data of some launch missions according to the two common engineering conditions. It is shown that the field calibration of the flowmeter has been achieved and the measurement precision of the filling system has been improved.
Propellant filling; Flow coefficient; Membership function; Least squares; Parameter identification
2016-11-04;
2017-04-14
国家自然科学基金青年基金(201507098)
V554+.4
A
1000-1328(2017)06-0655-07
10.3873/j.issn.1000-1328.2017.06.013
任永平(1966-),男,博士,高级工程师,主要从事航天发射地面设备、系统辨识等方面的研究。

