一种导航卫星的系统效能建模与分析方法

杨卓鹏，郑 恒，角淑媛，龚佩佩

(中国航天标准化与产品保证研究院，北京 100071)



一种导航卫星的系统效能建模与分析方法

杨卓鹏，郑 恒，角淑媛，龚佩佩

(中国航天标准化与产品保证研究院，北京 100071)

针对导航卫星的轨道机动调控、星地联动运行、可靠性要求高等特点以及整体性能评估问题，提出一种综合考虑各类中断、随机型与耗损型故障、性能等多种因素的系统效能建模与分析方法。该方法采用马尔科夫链构建导航卫星可用性模型；考虑威布尔分布和正态分布构建导航卫星可靠性模型；采用应力—强度算法将性能进行归一化处理；综合可用性、可靠性和性能归一化值开展系统效能建模与分析，使导航卫星系统效能研究由单因素(性能)拓展为多因素(可用性、可靠性和性能)。中轨道(MEO)导航卫星仿真算例表明，该建模与分析方法可为导航卫星设计优化决策提供量化依据，并可拓展应用于通信、气象、遥感等系列卫星，为其研制建设提供重要专业技术支持。

可用性；可靠性；性能；系统效能

0 引 言

导航卫星是卫星导航系统的重要组成部分，其系统效能高低直接决定着卫星导航系统能否顺利实现对用户承诺的精度、完好性、连续性和可用性等核心指标。开展导航卫星系统效能分析，对于识别导航卫星设计薄弱环节、优化导航卫星可用性与可靠性指标、改进星地保障运行方案等具有重要意义。

目前，国内外很多学者已对卫星系统效能进行了研究。文献[1]较早建立了系统效能与可用性、故障率的关系。文献[2-5]基于可用性可信性能力(Availability, dependability, and capability, ADC)模型对通信、遥感等卫星进行了系统效能建模与分析。文献[6-16]针对不同卫星类型，在构建系统效能评估体系的基础上，分别利用模糊理论、支持向量机、层次分析法、图论等方法，并有选择的融合专家知识开展系统效能研究。总结当前系统效能研究现状可以发现，研究对象主要集中在侦察、通信、遥感类卫星或其卫星网络，涉及导航卫星的文献较少；分析指标多为传输延迟、吞吐量、空间分辨率、图像容量等性能指标，联动分析卫星可用性、可靠性和性能关系的文献较少；研究思路一般为建立系统效能评估体系，并将评估体系中的性能指标优劣作为系统效能评价的主要指标，各项指标间的耦合分析有待改进；部分研究过程需综合专家知识，分析结果具有一定的主观经验性。

本文在上述研究成果的基础上，考虑导航卫星轨道机动调控、星地联动运行、系统效能关系复杂等特点，选择导航卫星可用性、可靠性、性能为构成要素，集成应用马尔科夫链、威布尔分布与正态分布、应力—强度等方法，进行导航卫星系统效能建模与分析，建立导航卫星运行状态、星地保障能力、可用性、可靠性及性能和系统效能之间的映射关系，并开展导航卫星薄弱环节识别与优化策略比对分析，提升导航卫星工作效率与应用效益。

1 导航卫星系统效能概念与分析思路

1.1 系统效能概念描述

系统效能定义为系统在规定的条件下和规定的时间内，满足一组特定任务要求的程度。它与可用性、可信性和固有能力有关。结合导航卫星特点，选择美国工业界武器系统效能咨询委员会(Weapon system effectiveness industry advisory committee，WSEIAC) 提出的系统效能表达式[17]：

E=A·D·C

(1)

式中：E表示导航卫星系统效能，A表示导航卫星可用性，D表示导航卫星可信性，C表示导航卫星能力。

1)导航卫星可用性

导航卫星可用性是指导航卫星能工作时间与能工作时间及不能工作时间的和之比，该指标描述导航卫星的可用时间率。对于中轨道(Medium Earth orbit,MEO)卫星而言，该指标是卫星理论过境时间和实际工作时间的综合反映，而实际工作时间又与中断事件密切相关。参考美国全球定位系统(Global positioning system, GPS)和欧洲空间标准化组织(European cooperation for space standardization, ECSS)相关标准[18-19]，导航卫星中断事件可分为四类[20]：短期计划(Short term scheduled，STS)中断、短期非计划(Short term unscheduled，STU)中断、长期计划(Long term scheduled，LTS)中断和长期非计划(Long term unscheduled，LTU)中断。

短期计划中断一般包括轨道机动、调频调相、备份系统切换等运行与维护活动。短期非计划中断一般指不可预见的单粒子翻转等硬失效或软失效，可通过硬件切换或软件重启等修复。长期计划中断一般指燃料耗尽等可预见的卫星寿命末期硬失效；长期非计划中断一般指不可预见的长期硬失效。

2)导航卫星可信性

导航卫星可信性指导航卫星在任务开始时可用性给定的情况下，在规定的任务剖面中的任一时刻，能够使用且能完成规定功能的能力。一般而言，导航卫星在单次执行导航电文的接收与生成、精密时间比对测量等任务的过程中不具备修复能力，故导航卫星的可信性转换为可靠性。

传统的导航卫星可靠性服从指数分布，即假设卫星发射后的运行状态与发射时一样。该假设未考虑导航卫星运行过程中的故障积累和老化机理，在描述导航卫星可靠性变化规律方面存在不足。因此，对传统的指数分布模型进行改进[21]，将导航卫星构成单元分为随机型故障单元和耗损型故障单元，导航卫星可靠性是上述两种故障单元可靠性的综合值。

3)导航卫星能力

导航卫星能力描述导航卫星在任务执行过程中持续工作的情况下，对任务目标的实现情况。导航卫星能力由性能表征。由于导航卫星是典型的多任务系统，其性能指标因业务类型而异。对于RNSS业务，包括上行注入和下行导航电文播发2项任务，相关综合性能指标包括：上注时间、注入频度、单次注入信息误码率、测距精度、信息传输速率等。对于RDSS业务，相关综合性能指标包括通信容量、授时精度、波束覆盖范围等。

1.2 建模与分析思路

建立系统效能和可用性、可靠性、性能等要素的映射关系，并进行指标要素波动分析，识别导航卫星的薄弱环节并提出设计改进策略。具体建模与分析思路见表1。

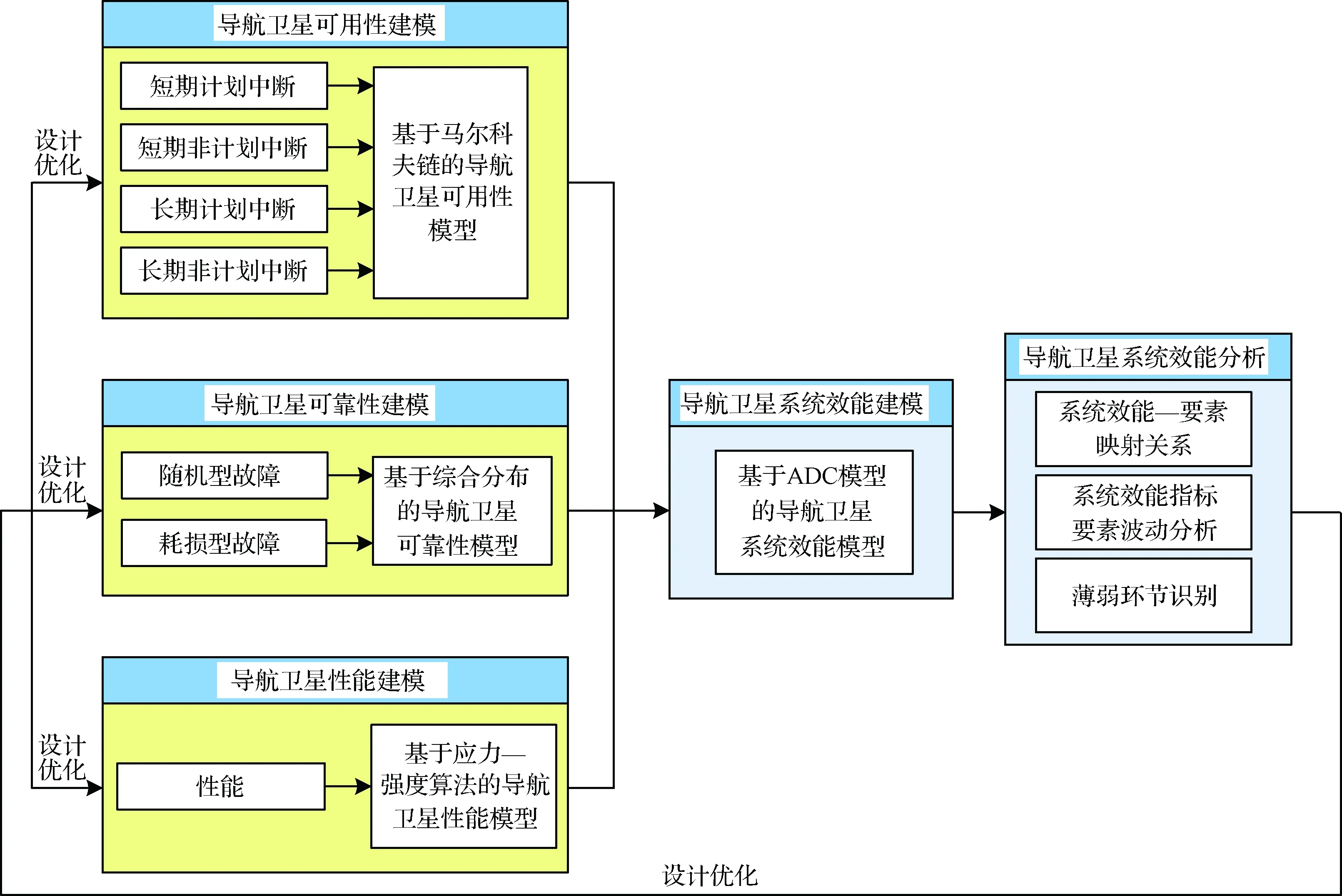
图1 导航卫星系统效能建模与分析流程Fig.1 Flow chart of system effectiveness modeling and analysis for a navigation satellite

2 导航卫星系统效能建模与分析

2.1 可用性建模与分析

构建基于马尔科夫链的导航卫星可用性模型，将导航卫星的短期计划中断、短期非计划中断、长期计划中断、长期非计划中断等各指标进一步分解为平均中断间隔时间(Mean time between outages ，MTBO)和平均中断修复时间(Mean time to repair outages，MTTRO)两项分指标。一般认为上述两项分指标均服从指数分布。图2为综合考虑各类中断的导航卫星可用性模型，图中S0表示导航卫星正常状态，S1i,i=1,2,3,4分别表示导航卫星的不同中断类型。λi=1/TMTBOi、μi=1/TMTTROi,i=1,2,3,4分别表示各类中断的故障率和修复率。

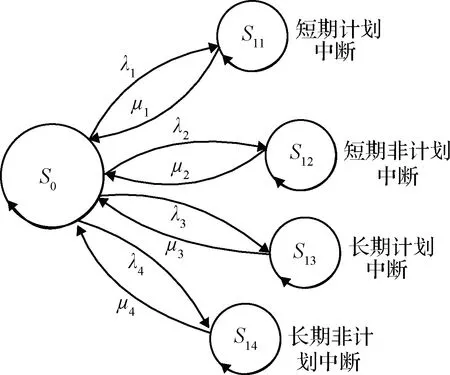
图2 基于马尔科夫链的导航卫星可用性模型Fig.2 Availability model of a navigation satellite based on Markov chain

合并各类中断的故障率和修复率，确定导航卫星的总故障率和总修复率为：

(2)

构建基于马尔科夫链的导航卫星可用性模型为：

(3)

式中：Pi(t),i=0,1为导航卫星处于运行或中断状态下的概率。

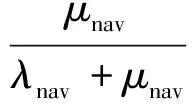
(4)

和稳态可用性：

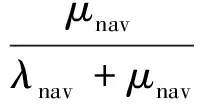
(5)

另一方面，导航卫星的可用性取决于其各类中断时间，设各类中断对应的稳态可用性分别为：ASTS(∞)、ASTU(∞)、ALTS(∞)、ALTU(∞)：

(6)

由式(5)～(6)可知，导航卫星稳态可用性与其各类中断稳态可用性的表达形式相同，建立相关映射关系：Anav(∞)=f(ASTS(∞),ASTU(∞),ALTS(∞),ALTU(∞))

(7)

抽取可用性表达式共性特征：

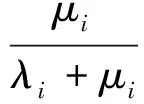
(8)

进一步转换为：

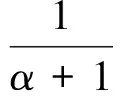
(9)式中：α称为维修时间比，其大小决定Ai。因此，可对各类中断的维修时间比进行比对和波动分析，识别导航卫星可用性的薄弱环节并提出改进建议。

2.2 可靠性建模与分析

根据导航卫星的运行状态，设随机型故障单元的可靠性服从威布尔分布，耗损型故障单元的可靠性服从正态分布，分别为：

Rr(t)=e-(t/α)β

(10)

式中：α为尺度参数，β为形状参数。

(11)

式中：μ为期望值，σ为标准差。

综合考虑上述两类可靠性分布，构建导航卫星综合可靠性模型：

(12)

2.3 性能归一化处理

根据导航卫星的设计要求，将性能进行归一化处理，归一化转换式为：

Cnav(t)= P(δ>σ)=1-P(δ<σ)=

(13)

式中：Cnav为性能归一化转换值，f(σ)为导航卫星实际性能指标，σ为应力，g(δ)为导航卫星要求的性能指标，δ为强度。

2.4 系统效能建模与分析

综合考虑导航卫星可用性、可靠性和性能归一化值，确定导航卫星的系统效能为：

Enav(t)=Anav(t)·Rnav(t)·Cnav(t)

(14)

3 算例分析

3.1 系统效能建模与分析

选取一颗MEO导航卫星，业务类别为RNSS，仿真构建系统效能模型，仿真时间间隔为0.5年，总时间为10年。按照业务特点，选择导航卫星可用性、可靠性、测距精度作为构成要素，开展系统效能建模与分析。

1)可用性

构建MEO导航卫星虚拟中断数据，如表1所示。

表1 MEO导航卫星的中断数据Table 1 Outages of a MEO satellite

结合表1，根据式(2)～(5)确定MEO导航卫星的瞬时可用性和稳态可用性，图3为10年内的瞬时可用性。由图3可知，MEO导航卫星的可用性在初始0.5年内逐渐下降，随后0.5年～10年时间内保持在91.33%左右。

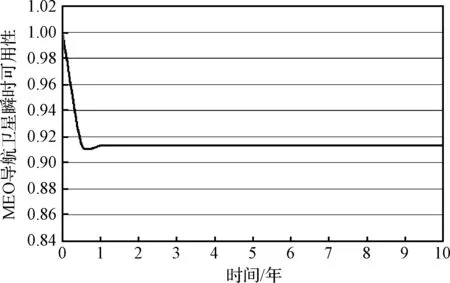
图3 MEO导航卫星10年期间瞬时可用性Fig.3 Instantaneous availability of an MEO satellite during 10 years

确定MEO导航卫星的稳态可用性：Anav(∞)=91.3252%。

根据式(6)～(9)进一步确定各类中断对应的稳态可用性和维修时间比，图4为各类中断对应的维修时间比。

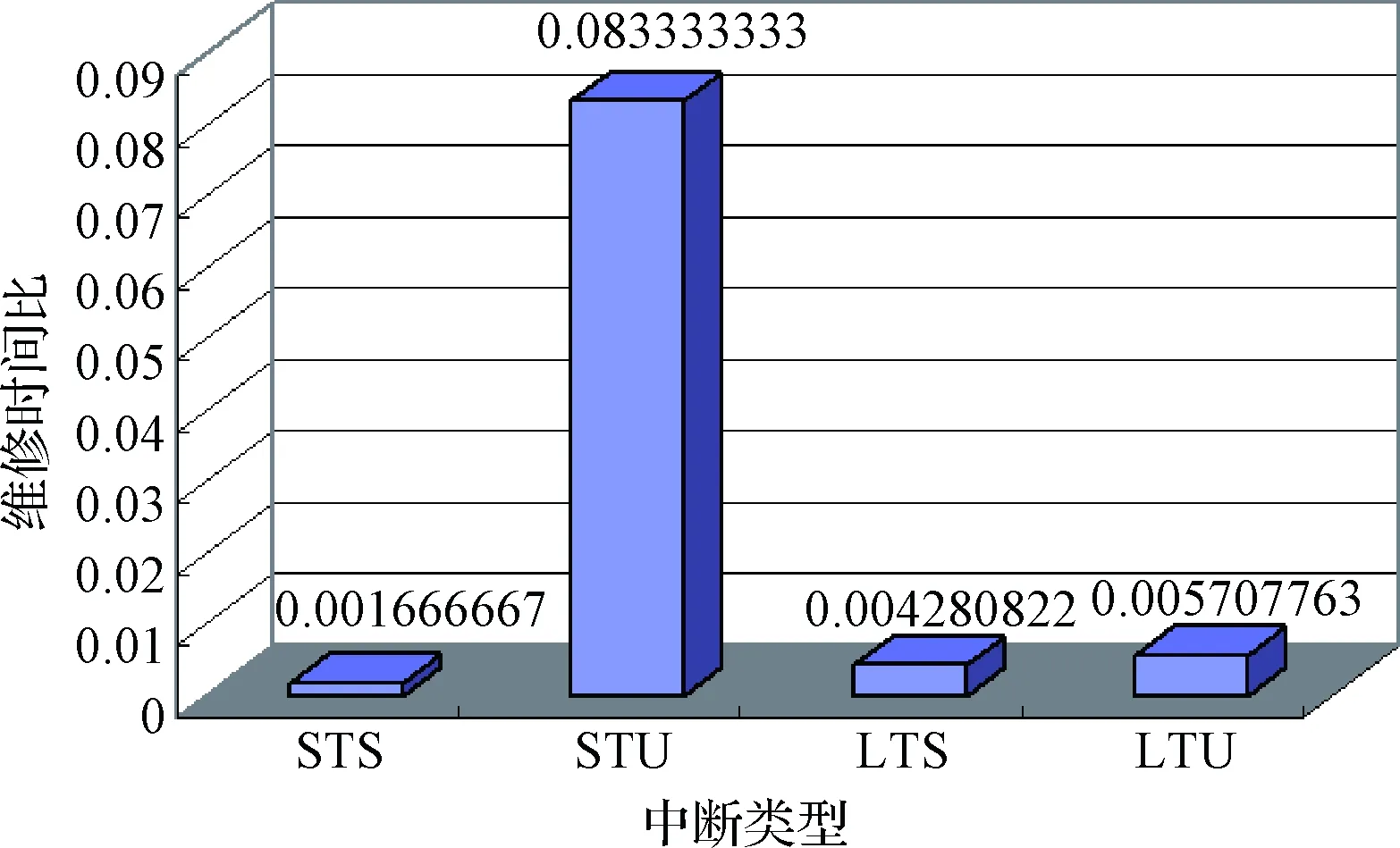
图4 MEO导航卫星各类中断对应的维修时间比Fig.4 Maintenance time ratio of an MEO satellite outages

由图4可知，短期非计划中断在维修时间比中占比较大,影响较为显著，因此短期非计划中断属MEO导航卫星可用性分析中的薄弱环节。

2)可靠性

对导航卫星按照随机型故障单元和耗损型故障单元进行结构分解。将导航任务处理单元、扩频应答机等电子类设备视为随机型故障单元，服从威布尔分布；将太阳电池阵、飞轮等光学类退化器件、机械类磨损设备视为耗损型故障单元，服从正态分布。

根据MEO导航卫星设计寿命要求和实际运行情况，参考GPS MEO卫星相关指标，确定其威布尔分布和正态分布的参数，如表2所示。

表2 MEO导航卫星可靠性参数Table 2 Index of a MEO satellite

结合表2，根据式(10)～(12)确定MEO导航卫星的综合可靠性，如图5所示。图中同时给出了威布尔分布和正态分布结果。

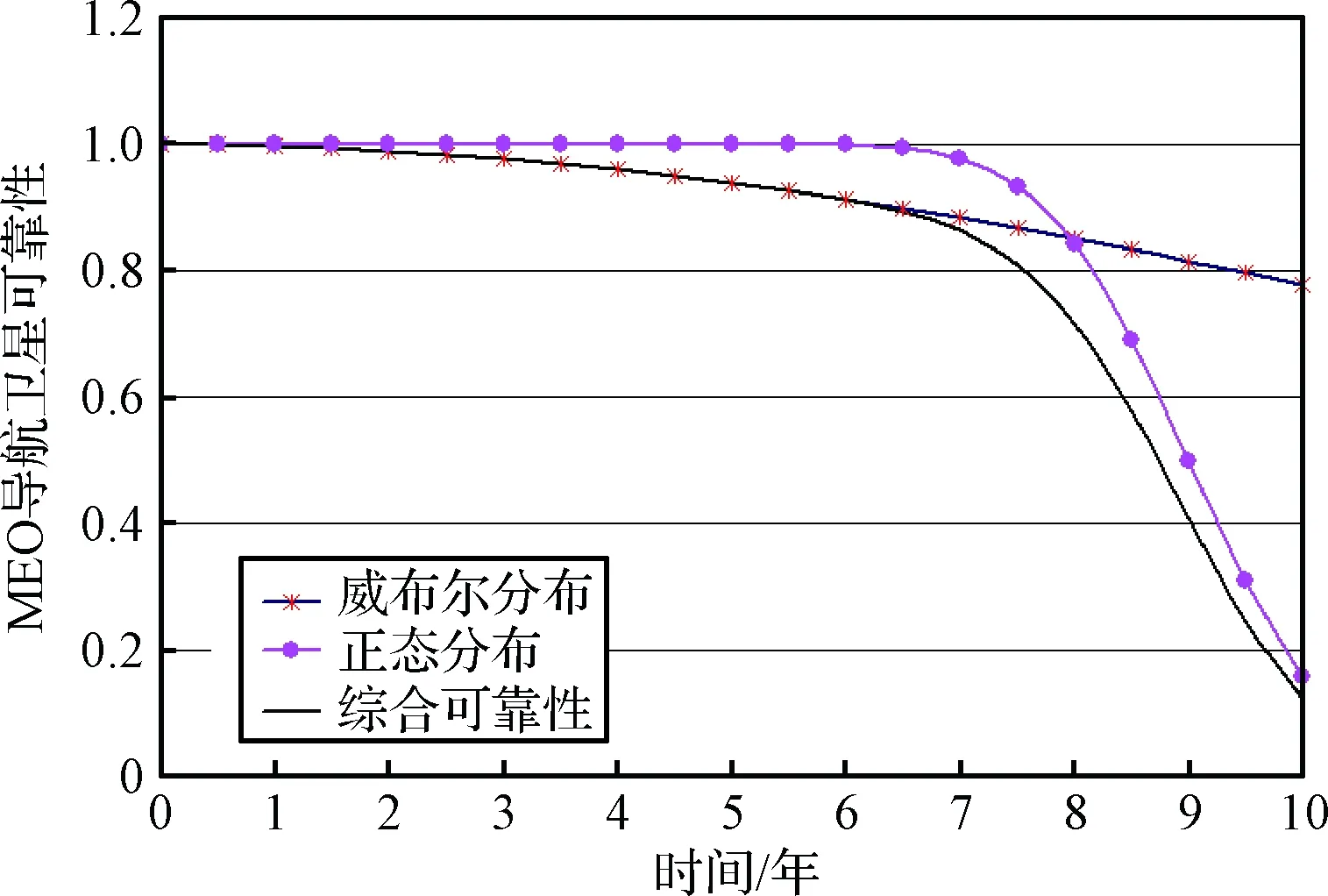
图5 MEO导航卫星10年期间可靠性Fig.5 Reliability of an MEO satellite during 10 years

由图5可知，MEO导航卫星的可靠性指标在前6年缓慢下降，至第6年可靠性仍保持在90%以上。从第6年开始，可靠性指标迅速下降，至第8年已不足80%，至第9年已不足50%，至10年末期可靠性指标仅为12.33%。

进一步分析，早期阶段，随机型故障单元的可靠性对MEO导航卫星的可靠性指标影响较大，随着时间的增长，耗损型故障单元的累积作用逐步显著，并成为影响MEO导航卫星可靠性的主导因素。

3)性能

本文选取测距精度作为RNSS业务性能指标。按照应力—强度算法进行测距精度归一化处理。MEO导航卫星在方案设计阶段会明确测距精度设计值，设设计值为强度，约定强度的均值为0.8，标准差为0.1，且保持不变。结合MEO导航卫星真实运行情况，仿真在轨运行过程中的测距精度实际值，设实际值为应力，约定初始阶段应力均值为0.3，标准差为0.1，且均值和标准差随着时间逐步增大。图6为MEO导航卫星10年期间测距精度应力—强度干涉情况。

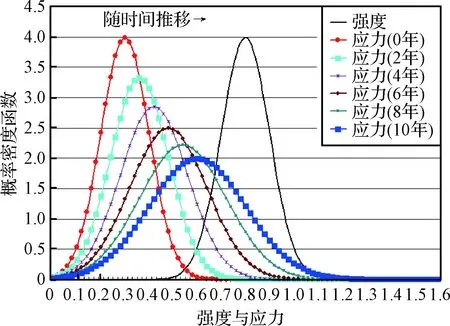
图6 测距精度应力—强度干涉情况Fig.6 Stress strength interference of ranging accuracy

由图6可知，应力的概率密度函数随着时间逐步逼近强度的概率密度函数，即归一化指标逐步降低。根据式(13)确定测距精度10年内的归一化指标变化情况，如图7所示。

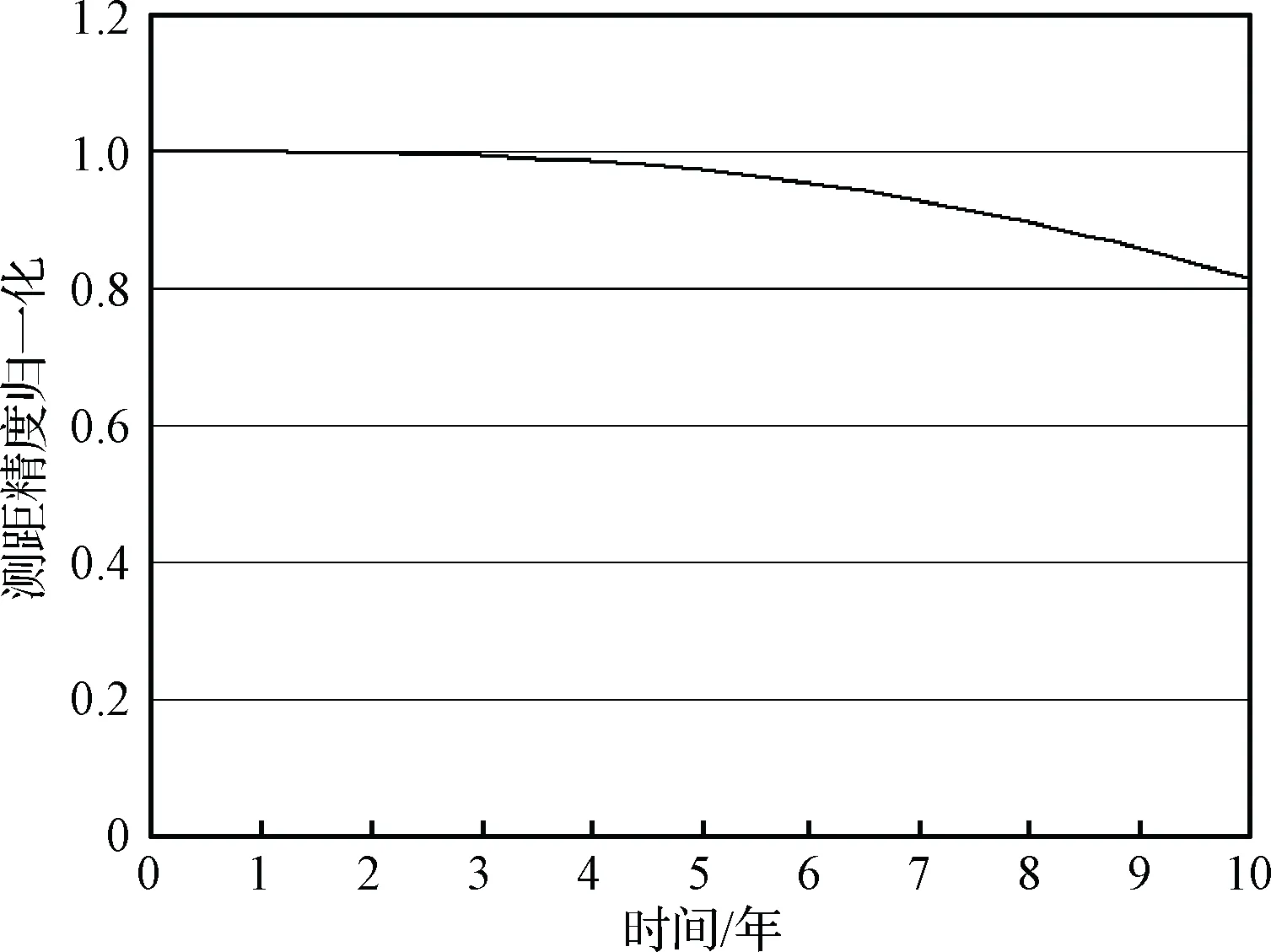
图7 MEO导航卫星10年内测距精度归一化指标Fig.7 Normalization of ranging accuracy for an MEO satellite during 10 years

由图7可知，归一化值随时间逐步降低。在0～3年内保持在0.99以上，至第5年为0.9739，至第8年已不足0.9，至第10年为0.8145。

4)系统效能

结合MEO导航卫星的可用性、可靠性、测距精度归一化值，根据式(14)确定其系统效能，如图8所示。由图8可知，MEO导航卫星系统效能在0～0.5年内出现较为明显的下降，即由99.98%降至91.23%；在0.5～5.5年内系统效能平稳下降，指标均保持在80%以上；随后系统效能迅速下降，至第8.5年已不足50%，至第10年，系统效能仅为9.17%。

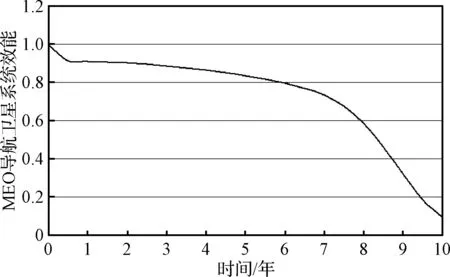
图8 MEO导航卫星10年运行期间系统效能Fig.8 System effectiveness of an MEO satellite during 10 years

3.2 优化策略比对分析

针对MEO导航卫星系统效能变化情况，开展薄弱环节分析。由图8可知，系统效能可分为三个阶段。第一阶段为早期阶段(0年～0.5年)，该阶段的主要影响因素为卫星可用性。第二阶段为平稳下降阶段(0.5～5.5年)，随机型故障单元可靠性和测距精度降低是效能下降的主要原因。第三阶段为迅速退化阶段(5.5～10年)，耗损型故障单元可靠性是效能下降的主要影响因素。第一阶段和第三阶段为系统效能明显变化时期，故对此两个阶段进行深入分析。

针对第一阶段，考查导航卫星的可用性。可以确定短期非计划中断是造成可用性初期下降的深层次原因。通过加强单粒子设计、电磁兼容设计、静电防护设计等措施，可有效提升短期非计划中断的平均中断间隔时间。同时，借助于充分的应急预案和快速反应机制，可进一步缩短短期非计划中断的平均中断修复时间。

针对第三阶段，考查导航卫星的可靠性。耗损型故障导致卫星后期可靠性和系统效能显著下降。按照假设的正态分布，决定耗损型故障波动趋势的参数是均值和方差，对应的物理含义为耗损型故障单元的寿命及其波动范围。因此，可将延长耗损型故障单元的寿命作为设计改进的重点。

综上，给出三种设计优化方案：

(1)将短期非计划中断的平均中断间隔时间提升1倍，同时将平均中断修复时间压缩30%；

(2)将耗损型故障单元寿命延长30%；

(3)综合方案(1)和方案(2)。

图9所示为三种设计优化方案与原方案的比对结果。

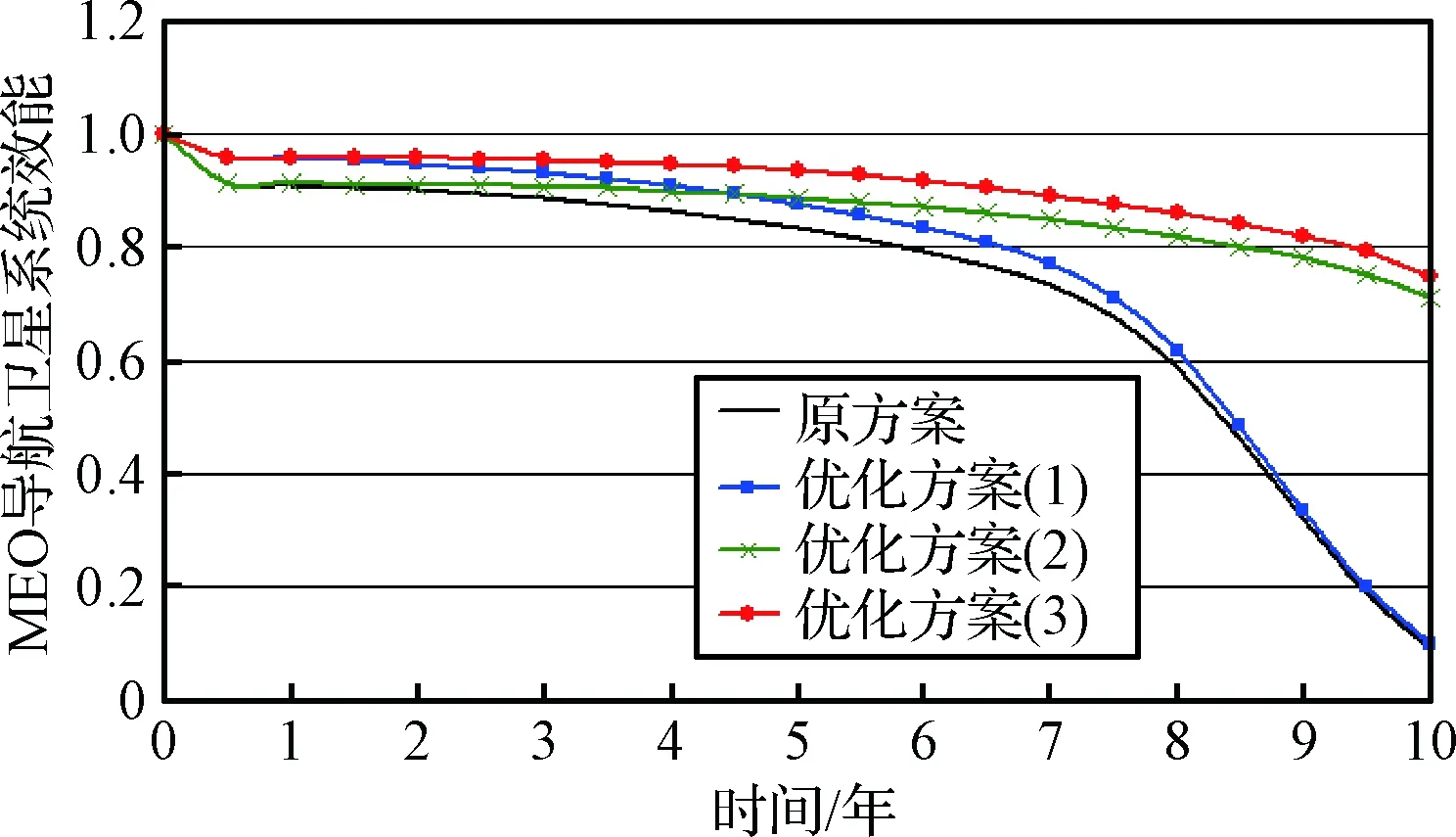
图9 MEO导航卫星系统效能方案比对Fig.9 System effectiveness comparison of different MEO designing schemes

由图9可知，相比于原系统效能(10年末期系统效能=9.17%)，方案(1)的优化效果并不明显(10年末期系统效能=9.65%)，方案(2)的优化效果十分显著(10年末期系统效能=71.07%)，方案(3)较方案(2)略有提升(10年末期系统效能=74.76%)。进一步分析，MEO导航卫星可用性除早期阶段的“陡坡式”下降外，在整个运行时间内基本保持平稳，且系统效能受可用性、可靠性、性能综合影响，仅改善一类中断指标，对提升整体系统效能并不显著。MEO导航卫星耗损型故障单元的寿命在后期阶段对可靠性降低起主导作用，延长耗损型单元的寿命对于提升整个MEO导航卫星的系统效能具有明显效果。

4 结 论

综合考虑导航卫星可用性、可靠性和性能，仿真构建其系统效能模型并开展设计优化方案比对，具体包括：

1)构建基于马尔科夫链的导航卫星可用性模型，建立了导航卫星可用性和各类中断可用性的映射关系；构建基于多种分布的导航卫星可靠性模型，指出耗损型故障单元是影响导航卫星可靠性的主导因素；采用应力—强度算法进行性能归一化处理，将性能指标波动情况转换为可靠性术语的表达形式。

2)综合导航卫星可用性、可靠性、性能归一化值，构建其系统效能模型，并给出延长短期非计划中断的平均中断间隔时间和压缩平均中断修复时间、延长耗损型故障单元寿命、以及综合上述两类的三种系统效能提升方案。分析结果指出：延长耗损型故障单元寿命对于提升系统效能的效果更为显著。

3)本文提出的系统效能分析方法可为导航卫星设计优化提供量化依据，同时，该方法还可进一步拓展应用于通信、气象等系列卫星，为各类卫星的研制建设提供重要专业技术支持。

[1] Francois F B, George Y N. Satellite systems availability and effectiveness[C]. Reliability and Maintainability Symposium, San Francisco, USA, Jan 24-26, 1984.

[2] Elhady A M. Remote sensing satellite system overall effectiveness analysis and modeling [C]. IEEE Aerospace Conference, Big Sky, USA, March 1-8, 2014.

[3] Liu C T, Xiang L, Zhu G Q. Effectiveness evaluation for Earth observation satellite system based on analytic hierarchy process and ADC model[C]. The 31st Chinese Control Conference, Heifei, China, July 25-27, 2012.

[4] 孟锦, 李千目, 张宏, 等. 基于ADC模型的侦察卫星效能评估研究[J]. 计算机科学, 2009, 36(6): 41-43. [Meng Jin, Li Qian-mu, Zhang Hong, et al. Effectiveness evaluation of reconnaissance satellite based on the ADC model [J]. Computer Science, 2009, 36(6): 41-43.]

[5] 王宇. 基于ADC模型的星座卫星通信系统效能评估技术研究 [D]. 长沙: 国防科技大学, 2007. [Wang Yu. Research on the effectiveness evaluation technology for constellation satellite communication system based on ADC modeling [D]. Changsha: National University of Defense Technology, 2007.]

[6] 沈宇飞, 王轶博, 矫贺明, 等. 一类模糊评价模型与通信卫星效能评估[J]. 哈尔滨工业大学学报, 2016, 48(4): 129-132. [Shen Yu-fei, Wang Yi-bo, Jiao He-ming, et al. A class of fuzzy evaluation model and the effectiveness evaluation of telecommunication satellites [J]. Journal of Harbin Institute of Technology, 2016, 48(4): 129-132.]

[7] 张力, 于睿, 金鑫, 等. 基于双犹豫模糊信息的军用卫星通信系统效能评估[J]. 舰船电子工程, 2016, 36(1): 97-142. [Zhang Li, Yu Rui, Jin Xin，et al. Effectivness evaluation of military satellite communication system based on dual hesitant fuzzy information [J]. Ship Electronic Engineering, 2016, 36(1): 97-142.]

[8] 朱建丰, 尤明懿. 基于多信息融合的海洋监视卫星侦察效能分析[J]. 系统仿真学报, 2014, 26(11): 2682-2691. [Zhu Jian-feng, You Ming-yi. Reconnaissance effectiveness analyses of ocean surveillance satellite based on fusing multidimensional information [J]. Journal of System Simulation, 2014, 26(11): 2682-2691.]

[9] Yang H T, Wang X M, Zhao H L. The modeling, simulation and effectiveness evaluation for communication networks of multi-layer satellite constellation[C]. 2006 International Conference on Computational Intelligence and Security, Guangzhou, China, Nov 3-6, 2006.

[10] Dong C X, Wu D W, He J. Study on method of satellite navigation system combat effectiveness evaluation based on rough fuzzy sets[C]. Chinese Control and Decision Conference, Yantai, China, July 2-4, 2008.

[11] Tang Y F, Yu X H. The effectiveness evaluation of nano-satellites used in military operations[C]. International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC), Dec 20, 2013.

[12] 冯书兴. 卫星系统综合效能分析研究[J]. 控制与决策, 2003, 18(6): 740-743. [Feng Shu-xing. Analyzing and studying of synthetic effectiveness for satellite systems [J]. Control and Decision, 2003, 18(6): 740-743.]

[13] 林琪, 李智. 基于拓扑特征的卫星网络效能评估[J]. 中南大学学报(自然科学版), 2013, 44(增2): 368-371. [Lin Qi, Li Zhi. Performance evaluation of satellite-network based on topologic characteristics [J]. Journal of Central South University (Science and Technology), 2013, 44(Suppl. 2): 368-371.]

[14] 田志新, 汤海涛, 王中果, 等. 基于星上动态指令调度的卫星使用效能提升技术[J]. 宇航学报, 2014, 35(10): 1105-1113. [Tian Zhi-xin, Tang Hai-tao, Wang Zhong-guo, et al. Satellite utility improvement technique based on dynamic on-board command scheduling [J]. Journal of Astronautics, 2014, 35(10): 1105-1113.]

[15] 项磊, 杨新, 张扬, 等. 基于层次分析法与模糊理论的卫星效能评估[J]. 计算机仿真, 2013, 30(2): 55-61. [Xiang Lei, Yang Xin, Zhang Yang, et al. Effectiveness evaluation for satellite system based on analytic hierarchy process and fuzzy theory [J].Computer Simulation, 2013, 30(2): 55-61.]

[16] 吴炜琦, 张育林. 海洋目标探测卫星的通用效能模型初探[J]. 宇航学报, 2006, 27(4): 814-818. [Wu Wei-qi, Zhang Yu-lin. The preliminary study of general effectiveness model of the ocean target detection satellite system [J]. Journal of Astronautics, 2006, 27(4): 814-818.]

[17] MIL-HAND-338B. Military handbook electronic reliability design handbook [S]. U.S. Department of Defense, 1998.

[18] U.S. Department of Defense. Global positioning system standard positioning service performance standard[R]. The 4th Edition, Washington DC, Sep 2008.

[19] ECSS-Q-ST-30-09C. Space product assurance-availability analysis[S].

[20] Rhonda S, Karl K. New and improved GPS satellite constellation availability model[C]. The 12th International Technical Meeting of the Satellite Division of the Institute of Navigation, Nashville, USA, Sep 14-17, 1999.

[21] Womack J. Revised block II/IIA lifetime predictions and the impact on block IIR/IIF replenishment planning[J]. Proceedings of the National Technical Meeting of the Institute of Navigation,1998:381-390.

通信地址：北京丰台区小屯路89号航天标准大厦(100071)

电话：(010)88108246

E-mail:yangzhuopeng88@163.com

A System Effectiveness Modeling and Analysis Method of Single Navigation Satellite

YANG Zhuo-peng, ZHENG Heng, JIAO Shu-yuan, GONG Pei-pei

(China Academy of Aerospace Standardization and Product Assurance, Beijing 100071, China)

Due to the high requirements of orbit control, satellite-station interactive operation, reliability, and performance assessment, a modeling and analysis method of system effectiveness for a navigation satellite is proposed, considering the outages, random and wearout faults as well as performance. The availability of a navigation satellite is confirmed based on the Markov chain, the reliability is analyzed considering the Weibull and Gaussian distribution, and the performance is normalized by the stress strength interference. The system effectiveness is modeled and analyzed by the factors mentioned above. The medium Earth orbit (MEO) simulation results have demonstrated that this method can be applied for design optimization, and be extended to communications, meteorological, remote sensing satellites.

Availability; Reliability; Performance; System effectiveness

2017-01-03;

2017-04-26

TN967.1

A

1000-1328(2017)06-0647-08

10.3873/j.issn.1000-1328.2017.06.012

杨卓鹏(1983-)，男，工程师，主要从事卫星导航系统可靠性建模与分析。