用数学思考引导小学生感受数学学习的魅力

雷英霞

摘 要：小学生学习数学的一个重要目标，是真正领略到数学的魅力，这对于小学数学教学来说是一个挑战，其是需要教师的教学策略作为支撑的。用数学思考来引导学生推开小学数学学习的大门，进而感受数学的魅力，是有效的策略。利用小学数学知识中的动静置换与空间理解，可以让学生体验到充分的数学思考，并在成就感的驱动之下激活自身的数学思维，从而让他们在数学学习中有更为良好的体验。

关键词：小学数学；数学思考；动静置换；空间理解；数学思维

小学生的数学学习过程应当是一个美丽的过程，这样的界定可以让自己所从事的小学数学教学变得美丽、智慧一些。这就意味着教师可以摆脱机械的知识传递，可以将数学美丽、智慧的一面呈现给学生。笔者以为，小学数学教师是应当有这种追求的，小学数学教师历来都是教学改革、课程改革的弄潮儿，解读当前活跃在小学数学课堂上的那些名师们，可以发现他们课堂上所绽放出来的智慧，是一般的数学课堂所不具有的。而从学生的角度来看，小学生的数学学习过程如何变得有趣且有收获，如何绽放出数学课堂应有的韵味，这是需要有效的学习策略作为支撑的。在笔者看来，重视学生在学习过程中的数学思考，可以帮学生推开小学数学学习的这扇大门，从而让学生领略到数学的有趣，领略到数学所包含的智慧。

一、数学思考体现在动静转换处

思考是人作为人的素养体现之一，数学思考是用数学的思维进行思考，数学思考的价值，对于小学生来说，是将形象的事物进行适当的抽象，以让其在大脑中形成的形象更为清晰与简洁。在小学数学学习中，学生的数学思考理论上是无处不在的，但更多的其实只是一种自然情境下的思考，而真正的数学思考的意蕴，往往是需要教师努力去发掘的。

动静关系是小学数学学习中比较常见的关系，动静转换常常可以促进学生进行有效的数学学习。动静理解在小学数学中可以是思维的动与知识的静，可以是数学实验的动与知识构建的静，可以是学生的动与教师的静，但无论是哪种动与静，只要很好地实现了转换，就能够激发学生的数学思考。

如在“三角形三条边的关系”（新人教版，下同，四年级下册）的教学中，要让学生认识到三条边之间的约束关系，教师可以在教学设计的时候确定这样的三对动静关系：第一对，呈现一个固定的三角形，并让学生猜想三角形三边的长度之间是否存在某种关系——这是形的静与思维的动；第二对，给出两根已知长度的小棒，如分别是10厘米与6厘米，如果需要提供第三根小棒构建一个三角形（可以给出若干长度的小棒让学生去选择），那这第三根小棒的长度是否要满足某个要求——这是数学活动（实验）的动与三角形三边关系理解的静；第三对，还是提供10厘米与6厘米的两根小棒，如果将其中一根折断并与另一根构成三角形，那如何折是否有技巧——这是变式的动与三角形三边关系理解的静。

在这样的三个教学环节中，动静是同时存在的，同时动静又是需要转换的：在第一个环节中，学生面前所出现的三角形是静态的，让学生对着这个静态的三角形去思考三边可能存在的关系，意味着学生要在大脑中对该三角形进行动态的思考，而最佳的思考方式就是一边不动，另两边像人的两只“脚”一样在不动的那个边上“劈叉”或“立正”（有学生说立正之后是个“瘸子”，这实际上是对非等腰三角形的通俗表达），这样就知道三角形的三边需要满足一定的关系了——这样的比喻是来自于课堂上学生的发言，这说明在学生的思维中，该三角形已经“动”了起来，因为学生所做的两个比喻，即劈叉与立正，其实都已经不是三角形了，真正的三角形存在这两者之间。尽管这个时候学生不能用严格的数学语言来描述三角形三边的关系，但已经大体上感觉到了两边之和必须大于第三边（而两边之差小于第三边是无法发现的）。

第二个环节需要学生实际动手完成三角形的构建。由于已经有了第一个环节作为支撑，学生的思维会更“活”一些，他们不需要做出太多的尝试就能够感觉到第三边的长度选择与已知两边长度的关系。比如说有学生在同组内其他学生选择了最长的那一根20厘米的小棒时，就立即判断：这一根肯定不行！因为他已经知道其长度超过了已有两根小棒的长度之和，肯定是不合适的。这里，三角形三边的关系作为一个知识点，已经静静地存在于学生的思维中，而学生的动手操作与动脑思考的动，则与静很好地呼应，从而构建了一个良好的动静共存的学习生态。

第三个环节与第二个环节类似，但从形式上来看，第三个环节与第二个环节是形异而神似的，这是一种数学变式思想的运用。变式之变，就是一种动，而三角形三边关系的重复可以视作一种静，这里仍然是一种动静转换，这样的转换类似于信息加工理论里的精加工，可以促进学生对三角形三边关系的进一步理解。

二、数学思考蕴含在空间理解里

数学是研究数与形的学科，在小学数学中，数形结合是学习的常态，尽管对学生不需要强调数形结合这个概念，但需要注意的是，学生对于形的认识其实异于数的认识的，因为学生小时候是经历了无数次“识数”的熏陶的，但对于形的认识则往往是自发的、自然的，因此在小学数学学习的过程中，教师要有意识地帮学生建立对形的一种空间理解（二维空间），这个理解的过程当然也是需要数的参与的，因此数形结合其实是空间理解的基础。

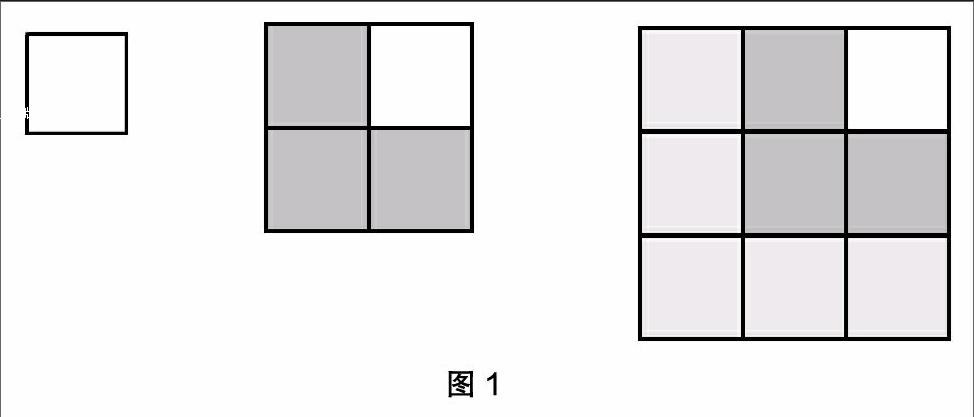
例如，在数学广角的“数与形”的研究过程中，当教师给出1+3=？1+3+5=？1+3+5+7=？等式子时，学生需要通过逐步计算来发现其中的规律，这只是基于數的打下本课学习基础的过程。其后，教师向学生呈现另一组图形（如图1）。

此时，学生可以通过比较发现，三个图形中的小正方形个数正好是1、4、9，而这个结果与刚才的运算存在重叠的地方，这个时候教师就可以引导学生的思维向空间转换：上一步中算式左边的加数与这里的图形之间是不是存在某种对应关系？而当学生发现算式左边的加数就是1+3，1+3+5时，学生是非常惊喜的，因为一个有规律的式子与一个有规律的图形之间竟然存在这样的对应关系，这对于小学四年级的学生来说，显然是一个意外的发现。在此基础上，教师可以给学生呈现一个边长为4个小正方形的大正方形，让学生写出对应的式子，则绝大多数学生都能够顺利地写出1+3+5+7。其后，教师帮助学生构建全面的空间理解：一个从1开始的连续奇数的和，既可以通过写式子的方式来呈现，也可以表现在由小正方形构成的大正方形里……教师可以进一步提出问题：如果给你一个现成的从1开始的连续奇数相加的式子，你能否判断出其对应的大正方形的边长是由几个小正方形构成的呢？这个问题可以将学生对空间的理解推向一个新的高度，因为学生需要对前几个图与算式（其实就是形与数）重新进行对比分析，进而发现结果，限于篇幅，这里就不赘述了。

在这样的学习过程中，学生的思维围绕空间进行了有效的转换，对于数与形的理解达到了一种默契的认识，这就是数形结合的效果，也是空间理解能力的提升。在此过程中，数形以令人惊讶的对应关系出现在学生的面前，激发兴趣是自然的，而学生由此领略数学的智慧亦是必然的。

三、数学思考存在于学生思维中

数学是思维的科学，亦是思维含量非常高的学科。在小学数学教学中，数学教学最终也是要指向学生的思维的。数学思维的表现形式是数学思考，数学思考也以数学思维为核心，因此对数学思考的研究是离不开数学思维的。

例如，教学“三角形的稳定性”是一个非常有意思的过程，因为稳定性严格来说并不是一个数学概念，但其又是三角形最基本的特征。在此教学中，最有效的策略当然是引导学生去比较，即在不提三角形稳定性的情况下给学生一个三角形、一个四边形，然后让学生去拉拉、搡搡，接着让学生说出自己的感觉以及发现。学生自然会用生活语言说出：三角形拉不动，而四边形可以“变形”。那教师可以追问：如果在一个建筑中，你觉得是用三角形好还是用四边形好呢？学生在生活经验的作用之下，自然会认识到三角形可以让房子更为稳固。请注意，一旦学生说出类似于稳固的词，那教师就要引导学生将其向“稳定性”过渡，这也是一个思维过程，也是用相对统一的语言描述三角形特征的过程。

对于思维在数学学习中的作用，小学数学教学历来有重点研究的传统，这里不需要赘述。只是要强调一点：为了让学生真正走进数学的大门，并窥得数学学科的魅力，数学教学设计与课堂教学只有围绕学生的思维来进行，才能彰显数学学科的魅力，也就是说只有思维才能激发学生对数学学习的兴趣，进而形成一种良好的数学学习直觉，这种直觉的作用是其他的说教所无法比拟的。可以肯定地讲，数学思维几乎就是学生领略数学魅力的最重要的因素！