地铁线路平面设计切圆法及其应用

卓文海

(广州地铁设计研究院有限公司， 广东 广州 510010)



地铁线路平面设计切圆法及其应用

卓文海

(广州地铁设计研究院有限公司， 广东 广州 510010)

为提高地铁线路平面精调效率，避免调线后出现相邻区段控制点线位偏差，利用切圆法通过建立与圆曲线相切的辅助线进行指定角度的切圆旋转，通过协同调整交点坐标与切线方位角关系进行平面优化。结果表明：1)在调整相邻区段线位时，切圆法可以完全不影响已稳定曲线部分的线位；2)利用切圆法调整线位，对既有曲线的变化只是单端减短或增加圆曲线的长度；3)在设计阶段，对于控制点众多的连续曲线区段的平面选线，切圆法具有较强的实用性；4)在施工过程中，当发生隧道平面掘进偏移事故时，切圆法能够极大程度地提高调线的工作效率，能短时间内提出指导后续推进的调整方案，降低盾构停机所造成的工程风险。

城市轨道交通；调线；切圆法；线路平面设计

0 引言

传统的地铁线路平面调线方法主要有：1)调整曲线两侧直线偏角；2)改变曲线半径、缓和曲线长度等参数；3)调整交点坐标[1]。

国内很多学者对平面调线进行过研究和总结。杜昊璇[2]在分析调线调坡设计时，以哈尔滨1号线交通学院至桦树街站区间为例，隧道平面偏差达131 mm，在不改变曲线半径的情况下，通过调整2处缓和曲线长度，将偏差调整至73 mm。李建斌[3]在分析圆形隧道调线调坡设计时，以深圳地铁5号线翻身站至灵芝站区间右线为例，水平方向普遍侵限100～350 mm，通过采用移动交点位置、调整曲线要素等方法来调整线路平面，将偏差控制在69 mm以内。陈菊[4]总结了平面调线的一般方法：1)对于两头切线方向偏差不大，而曲线地段偏差超出范围的地段，可采取偏角不变、调整曲线半径或缓和曲线长度的方法进行调整；2)对直线(含部分曲线)存在同向偏差且数值相当的地段，可采用切线平移的方法进行调整。李洪强[5]提出了旋转夹直线偏角，结合旋转夹直线偏角、曲线半径及缓和曲线长度三者叠加的调整方法，通过同时调整曲线多个要素进行优化，并在苏州地铁1号线调线过程中进行运用。赵强[6]在武汉地铁2号线调线中，越江区间过江南明珠园段，左线采用R=360 m、l=60 m的右偏曲线，在掘进过程中发生300 mm的偏移，通过调整半径、缓和曲线长、切线偏角等方法进行多次试算，提出R=359.9 m、l=60 m的调整方案，避免侵限。吴爽等[7]为提高地铁平纵设计工作效率，在CAD系统基础上，利用VS.NET、ARX2006和AUTOLISP等编程工具，开发了地铁平纵面CAD系统MetroExpress，其平面数据结构是运用交点法进行描述，其线元数据包括直线、圆曲线半径、缓和曲线、切线方位角等。

以上方法均是通过单一调整曲线某一要素，或同时调整多个参数进行调线，但始终未利用参数间的关系，建立稳定既有曲线线位的调整方法。本文提出切圆法，在曲线前后直线段线位调整的情况下，可控制曲线段整体线位不变，避免对已稳定区段方案的影响，极大程度地提高了平面线路优化设计工作的效率。

1 切圆法

1.1 主要特点

曲线的主要参数有交点坐标、圆曲线半径、缓和曲线、线路偏角、外距和切线长[8]等(如图1所示)。常规的移动交点法及平行夹直线法之所以会造成曲线段线位的变化，是因为简单改变了曲线交点的坐标或者曲线两端线路的偏角。切圆法相对于常规的移动交点法及平行夹直线法，可以实现调整前后线位改变，而曲线某些区段整体线位不变的效果。

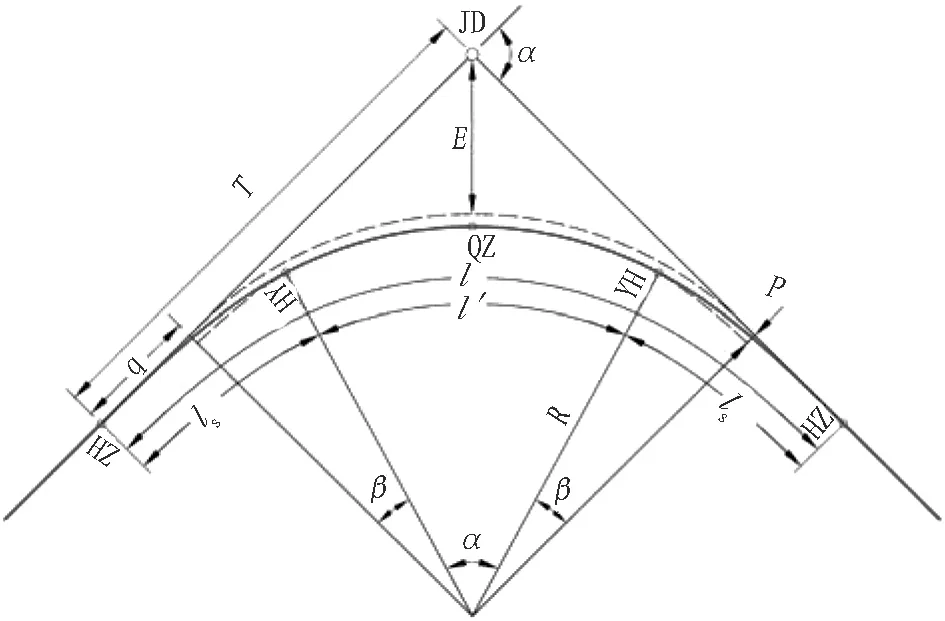
ZH为直缓点；HY为缓圆点；YH为圆缓点；HZ为缓直点；α为加缓长后的曲线偏角；R为圆曲线半径；β为缓和曲线偏角；P为内移距；q为切线增长；T为切线长；E为外距；D为切曲差(D=2T-l)。
图1 曲线要素示意图
Fig.1 Sketch of curve elements

1.2 设计原理

一旦曲线的交点坐标、切线方位角、半径及缓和曲线长度(采用统一的三次抛物线型)确定了，也就确定了曲线的线位[9]。切圆法通过旋转切线，保持调整后的直线线位始终与该圆曲线相切，而另一端切线、前缓和曲线长度、半径均不变。

采用切圆法对交点坐标及切线进行协同调整，调整后只是根据线位变化的幅度改变了后缓和曲线线位，缩短或延长了圆曲线长度，而对于圆曲线其他区段、前缓和曲线及前直线的线位，均未产生变动。

1.3 调线方法

1.3.1 明确控制点位置，确定调整方向

调整线位的目的，一是保持曲线整体线位不变，避免影响已稳定区段的线型；二是对与曲线相邻的直线段进行微调。根据现阶段方案线位与新增控制点的平面关系，应对直线段的偏移方向(顺时针方向为负，逆时针方向为正)及偏移角度有大致判断。

1.3.2 绘制辅助切线

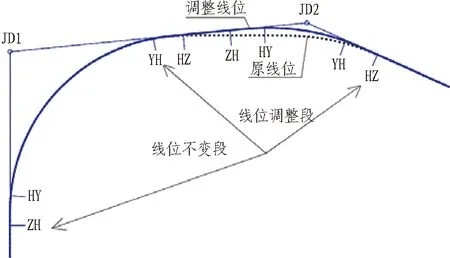
在需要保持不变的曲线交点JD1，与需要调整的直线段相连的另一交点JD2之间，绘制辅助直线AB(圆曲线的切线外偏内移值P)，该直线即为曲线的切线。为使相邻线路调整后该曲线线位不变，需要将直线AB以圆曲线圆心为旋转的基点进行旋转，得到直线A′B′(如图2所示)，该直线是在圆曲线切线基础上外偏P值(内移值)而得的辅助线。在旋转过程中，可以根据控制点位置，通过观察切线的实时线位进行手动粗略定位， 也可以输入需要旋转的角度(顺时针方向为负，逆时针方向为正)，进行精确微调。

ZH为直缓点；HY为缓圆点；YH为圆缓点；HZ为缓直点。
图2 选取切线示意图
Fig.2 Sketch of tangent line selection

1.3.3 定位调整线位

辅助线A′B′的位置能满足避让后续控制点时，已经实现对JD1和JD2坐标的重新定位，直线A′B′与两交点所对应的另一切线分别相交的JD1′与JD2′即为目标方案的2个新交点。可通过移动交点法分别调整2处交点，也可以通过平行夹直线法，将直线AB作为需要移动的初始线位，以直线A′B′作为基准直线，输入“0”线间距，实现重合，达到调线的目的(如图3所示)。

2 工程实例

2.1 沿线环境

深圳地铁9号线香梅站至景田站区段为福田成熟建成区，建筑密集，高楼林立，路口西北侧为鲁班大厦(地上30层，地下1层，人工挖孔灌注桩，桩长30 m)、香蜜新村(地上7层，条形基础)及市政大院住宅楼(地上8层，人工挖孔灌注桩，桩长大于18 m)。景田路两侧分布有擎天华庭高层住宅楼(地上46层，地下2层，人工挖孔灌注桩，桩长24 m)、天平大厦(地上28层，地下1层，人工挖孔灌注桩，桩长23 m)、景田综合市场、妇儿大厦等。

ZH为直缓点；HY为缓圆点；YH为圆缓点；HZ为缓直点。
图3 调整前后线位对比图
Fig.3 Line position before and after adjustment

2.2 线路方案

2.2.1 原方案

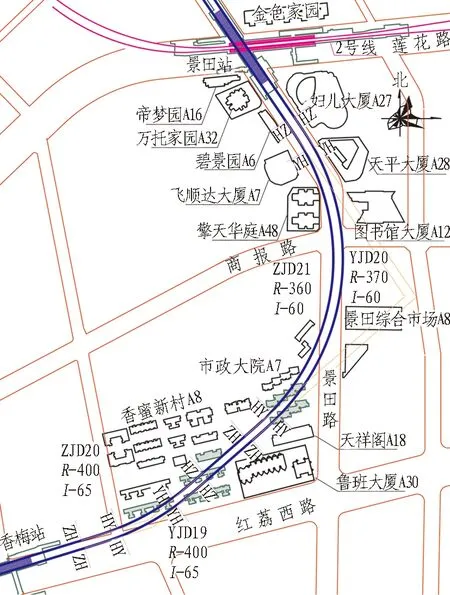
区间由红荔西路转至景田路敷设，因道路走廊限制，线路转角达77°。景田站与已运营的2号线侧岛T型换乘，本线为岛式站，换乘节点已预留，景田站以南线位可调空间小。线路平面在该区间采用了半径为400 m和370 m的2处小曲线，平面避让高层建筑，由鲁班大厦北侧经过，下穿3栋香蜜新村住宅楼及2栋市政大院住宅楼(如图4所示)。

ZH为直缓点；HY为缓圆点；YH为圆缓点；HZ为缓直点。
图4 原方案线路平面图
Fig.4 Original plan of metro line

由于早期阶段未搜集到鲁班大厦具体地下室基础图，右线隧道与建筑主体净距按12 m控制，可以避免下穿香蜜新村26号楼。随着项目的推进，通过定测数据揭示，其地下室北侧外扩最大处达12.4 m，且采用桩径为1.5 m、桩长为30 m的人工挖孔灌注桩无法竖向避让，隧道与桩基相冲突，须采取桩基托换；靠近景田段，隧道与擎天华庭、天平大厦桩基净距仅为 2.26 m和6.9 m，同时，线位受2号线预留节点限制，基本无调整空间。

2.2.2 切圆法优化方案

为了避免托换鲁班大厦桩基，降低工程风险及投资，通过切圆法，在不影响景田站南侧线位的情况下，对该段线路平面进行优化。

定义靠近香梅站一侧为曲线1、靠近景田站为曲线2，连接右线2个交点建立辅助线AB，以曲线2的圆心为基点，向顺时针方向旋转4°(即旋转角度为-4°)，辅助线A′B′与鲁班大道西北角地下室桩基净距约3.9 m，该处隧道位于强风化及中风化花岗岩地层，优化后线位具有较好的可实施性及安全性，如图5和图6所示。

ZH为直缓点；HY为缓圆点；YH为圆缓点；HZ为缓直点。
图5 切圆法示意图
Fig.5 Sketch of tangent circle method

通过平行夹直线功能将右线与辅助线重合。为确保左、右线隧道净距处于相对安全的实施环境中，控制隧道净距在1倍盾径的情况下[10]，需下穿香蜜新村26号楼，该楼为条形浅基础。香梅站东侧采用坡度为25‰、坡长为320 m的坡段下坡，隧道顶与香蜜新村基础净距约17.9 m，与市政大院住宅桩底净距约2.97 m。市政大院及其以北高层密集区段平面线位均未变化。由此可见，使用切圆法，在该区段线位优化中可以较好地体现出其优势，如图7和图8所示。

ZH为直缓点；HY为缓圆点；YH为圆缓点；HZ为缓直点。
图6 优化方案线路平面图
Fig.6 Optimized plan of metro line

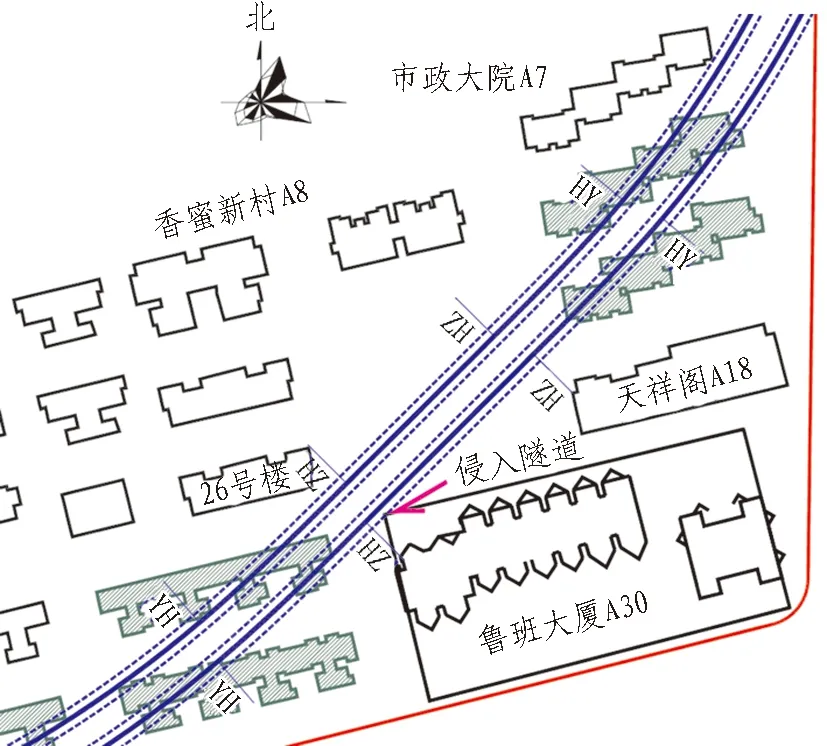
ZH为直缓点；HY为缓圆点；YH为圆缓点；HZ为缓直点。
图7 原方案净距图
Fig.7 Original plan clearance

3 应用拓展

利用切圆法能够实现对曲线某侧线路调整的条件下，完全不影响圆曲线及另一侧缓和曲线的线位。该方法可在设计优化过程中提高工作效率，同时，也可在调线调坡工作中得到较好的应用，可以在辅助线旋转时，输入具体的旋转参数，对平面进行精细化的调整。

此外，在施工过程中，由于地下工况变化等不可预见因素，小半径曲线段掘进过程中容易发生隧道偏移。若监测发现偏移较大时，需要立即停止掘进，进行隧道断面测量[11]，分析后续趋势，必要时需要调整线位，以适应现场情况。当偏移发生在曲线中部时，无法通过插入一段曲线进行调整，若通过调整曲线半径、缓和曲线参数、移动交点等方法，都将影响到未发生偏移的已实施段。切圆法能在此种情况下发挥其重要的优势，可以避免拟合推进趋势后造成已实施段线位的偏移。

ZH为直缓点；HY为缓圆点；YH为圆缓点；HZ为缓直点。
图8 优化方案净距图
Fig.8 Optimization scheme clearance

4 结论与建议

切圆法与传统调线方法的区别之处在于该方法并非独立改变曲线的某个或多个参数值，而是保持几个参数之间的关系进行协同调整，建立在圆曲线切线基础上外偏P值(内移值)的辅助线，在调整相邻区段线位时，可以完全不影响已稳定曲线部分的线位，对既有稳定曲线的变化只是单端减短或增加圆曲线的长度。

切圆法可以在线路设计阶段、施工过程发生偏差时或者隧道贯通后的调线调坡阶段，较好地发挥其优势。在设计阶段，可以提高控制点众多的连续曲线区段的平面设计效率。在施工过程中，当发生隧道平面掘进偏移事故时，切圆法能较好地结合既有隧道与掘进趋势进行拟合，提出合理的推进建议，以指导施工，降低盾构停机所造成的工程风险。隧道贯通后，根据断面测量数据，发现隧道平面侵限时，可以进行精细化微调。

建议在基于CAD平台的地铁平纵辅助设计软件中，补充切圆法的拓展操作，实现调整过程中的可视化联动效果，进一步改善调线效率。同时，建议研究以隧道全断面扫描数据为基础，运用BIM技术，进行侵限碰撞检查，结合切圆法及传统平面调线原理，实现平面调线与纵断调坡的联动设计。

[1] 叶霞飞，顾保南.轨道交通线路设计[M].上海：同济大学出版社， 2010.YE Xiafei,GU Baonan.Rail transit line design[M].Shanghai:Tongji University Press,2010.

[2] 杜昊璇.城市轨道交通施工完成后的调线调坡设计研究[J]．地下工程与隧道， 2015(2):52-59.DU Haoxuan.Study of alignment and slope design of urban rail transit after completion of construction [J].Underground Engineering and Tunnels,2015(2):52-59.

[3] 李建斌.圆形地铁隧道调线调坡设计研究[J]．铁道标准设计，2015(3):90-93.LI Jianbin.Research on fine-tuning of line and slope of circular metro tunnel[J].Railway Standard Design,2015(3):90-93.

[4] 陈菊.城市轨道交通线路设计中的调线调坡技术研究[J]．铁道标准设计， 2014(3):25-28.CHEN Ju.Technical study of route alignment and gradient adjustment in route design of urban rail transit [J].Railway Standard Design,2014(3):25-28.

[5] 李洪强.苏州轨道交通调线调坡技术研究[J].铁道建筑技术， 2013(11):38-40.LI Hongqiang.Research on line and slope adjustment technology of Suzhou Rail Transit [J].Railway Construction Technology， 2013(11):38-40.

[6] 赵强.武汉2号线调线调坡设计研究[J]．铁道工程学报， 2013(10):100-105.ZHAO Qiang.Research on adjustments of track and gradient of Line 2 of Wuhan Metro[J].Journal of Railway Engineering Society， 2013(10):100-105.

[7] 吴爽，田连生.地铁平纵面CAD系统研究与开发[J].铁道勘察， 2014(3)：85-87.WU Shuang,TIAN Liansheng.Development and research on CAD system of metro horizontal and profile [J].Railway Investigation and Surveying,2014(3)：85-87.

[8] 毛保华.城市轨道交通规划与设计[M].北京：人民交通出版社， 2011.MAO Baohua.Urban rail transit planning and design[M].Beijing:China Communications Press,2011.

[9] 欧阳全裕.地铁轻轨线路设计[M].2版.北京：中国建筑工业出版社， 2016.OUYANG Quanyu.Metro light rail line design[M].2nd Edition.Beijing:China Architecture & Building Press,2016.

[10] 地铁设计规范:GB 50157—2013[S]．北京:中国标准出版社， 2014． Code for design of metro:GB 50157—2013[S]．Beijing:Standards Press of China， 2014．

[11] 李连生．地铁既有线改扩建工程中线路调线调坡测量技术的研究与应用[J]．城市轨道交通研究， 2013， 16(3) :107-111． LI Liansheng．Survey technology in adjusting route alignment and gradient in the improvement of existing subway lines[J]．Urban Mass Transit， 2013， 16(3):107-111．

Design and Application of Tangent Circle Method for Metro Lines Design

ZHUO Wenhai

(GuangzhouMetroDesign&ResearchInstituteCo.,Ltd.,Guangzhou510010,Guangdong,China)

In order to improve the plane fine adjustment efficiency of metro lines and avoid line position deviation of control point of adjacent sections after line adjustment,a tangent circle method is adopted.The results show that:1) When adjusting the line position of the adjacent sections,the line position of the section with stable curve will not be affected.2) By using tangent circle method,the existing curve shortens at one end and increases in length.3) In the design phase,the tangent circle method is the most practical for plane line selection of continuous curve with plenty of control points.4) In the construction process,by using the tangent circle method when the deviation occurs to tunnel plane excavation,subsequent line adjustment scheme can be proposed and the engineering risk induced by shield stop can be reduced.

urban rail transit; line adjustment; tangent circle method; plane design of metro lines

2017-02-08;

2017-03-21

卓文海(1987—)，男，福建寿宁人，2009年毕业于长沙理工大学，交通工程专业，本科，工程师，现从事轨道交通规划和线路设计工作。

E-mail:zhuowenhai@dtsjy.com。

10.3973/j.issn.1672-741X.2017.06.012

U 452.1+3

B

1672-741X(2017)06-0730-05