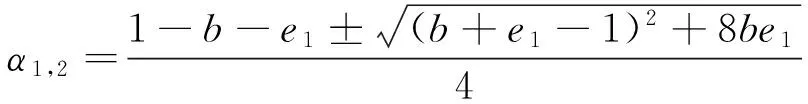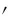食饵捕食模型的周期性行波解的存在

熊 军

(兰州交通大学 数理学院, 甘肃 兰州 730070)

食饵捕食模型的周期性行波解的存在

熊 军

(兰州交通大学 数理学院, 甘肃 兰州 730070)

处理了关于修正的食饵捕食者扩散反应模型的行波解的有效解析.通过分析该模型的指数多项式特征方程的根,得到了模型的唯一正稳定状态的渐近稳定性的重要条件.

食饵捕获模型; 扩散; 稳定性; 周期行波

0 引言

考虑以下关于周循环样本的简单反应扩散模型

(1)

包括互相影响的种类,各自拥有种群的密度u和v,其中f(u,v)和g(u,v)模拟局部活动,密度u和v代表食饵和捕食者,宿主和被宿主等等．其中x是空间坐标,t表示时间．我们把焦点放在循环样本上,则存在动力函数f和g满足空间上一致连续方程组:

则方程组有一个稳定的周期解(极限环)在不稳定与稳定共存之间产生.对于3种或以上的种类的模型,周期行波解的定理同样适用．以下是基于Leslie-Gower and Holling type II schemes的食饵捕获模型的反应扩散系统[1]:

(2)

其中式(2)的所有变量都为正.函数u(x,t)和v(x,t)分别表示食饵和捕食者的密度,d1、d2是反应扩散系数,b1是测量食饵种群(u)之间的竞争强度,是食饵(u)的每头数的减少率,k1、k2是测量环境给食饵和捕食者提供的资源的量,r1、r2描述的是食饵的成长率,a1、a2表示极值.则如下是一个常微分方程:

(3)

其中初值条件:x(0)>0，y(0)>0．这两种食物链模型描述的是捕食(食饵)样本x是捕食者y的食物．式(3)是如下时滞的方程组所组成的系统[2]:

(4)

对所有t>0都成立,这里离散的时滞数τ>0和捕食者的密度的负反馈一致．

1 稳定状态和稳定性

反应扩散系统如下:

(5)

进一步简化,取

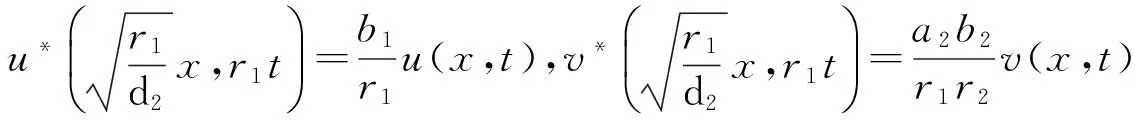
然后使用u,v,x,t表示,得

(6)

可以证明反应扩散系统(6)产生一个动力系统在稳定的Banach空间上是个好的生态系统模型[3]．令

F=(F1,F2),U=(u,v),D=diag[d,1],

其中

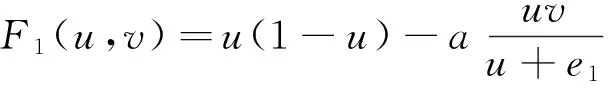
考虑边界条件,可以把系统(6)写成如下形式

(7)

(8)

(9)

则式(9)是如下抽象线性微分方程组在X1上的解.

(10)

由半群的另外一个性质有，对每个t>0时,Tu(t)和Tv(t)是紧算子,则得到如下偏微分方程组

(11)

这是关于F1=F2=0的初值有界值问题(7)的古典解[4]．

令T(t):X→X,T(t)=Tu(t)×Tv(t),则T(t)是X上算子的一个半群,由在定义域D(A)=D(Au)×D(Av)上和算子A=Au×Av的作用下所产生,并且U(x,t)=[T(t)φ](x)是以下线性系统的解,

(12)

由于非线性项F在U上是二次连续可导．因此,我们可以定义映射[F*(φ)](x)=F(φ(x))是X到自身的映射,方程组(7)可以看成是在X上的一个常微分方程组,记为

(13)

因此,通过限制一些条件,如φ∈D(A)，可以获得式(13)的一个解z(t),则z(t)可能写成如下形式

(14)

另外,

(15)

T(t)XΛ⊂XΛ,t≥0

(16)

定理1 对每个φ∈XΛ,系统(6)有一个唯一的平衡解z(t)=z(φ,t)∈XΛ和一个古典解U(x,t)=[z(t)](x).甚至,通过系统(6)的诱导,在流型ψT(φ)=z(φ,t)下,集合XΛ是正变量集．

证明 系统(6)有4个平衡点:E0=(0,0),E1=(1,0),E2=(0,e2),E*=(u*,v*)和没有扩散的常微分方程组的系统(6)的平衡点一致,其中

(17)

v*=u*+e2

(18)

在没有扩散下,平衡点E0处,食饵和捕食者之间的关系可能处于不稳定状态,在没有捕食者的情况下,E1是个鞍点.若ae20,则在E*处,食饵和捕食者之间关系达到渐近平衡,并且若p(u*)<0,在E*处,食饵和捕食者之间关系没有达到平衡;其中

p(x)=2x2+(b+e1-1)+be1

(19)

进一步,若在E*处,系统是渐近稳定,但是若b+e1-1<0,并且α1

特别地,如果e1-1≥0,在E*处,系统是全局渐近稳定[5]．如果b+e1-1≥0,则系统没有极限环．为了找到系统(6)的行波解的存在性[6],我们假设解具有如下形式

u(x,t)=u(x+ct)和v(x,t)=v(x+ct),

其中s=x+ct,c是波速.则系统(6)可以写成

(20)

(21)

式(21)有4个平衡点E0=(0,0,0,0),E1=(1,0,0,0),E2=(0,e2,0,0),E*=(u*,v*,0,0),其中u*,v*由式(17)和式(18)中所给定．系统(21)在平衡点(f,g,0,0)附近的线性系统如下

(22)

此时对应的特征矩阵和对应的特征方程为

Q(λ,d)=λ4-(c+γ)λ3+(cγ-α-υ)λ2+(γυ+αc)λ+αυ-βμ

(23)

其中

对于βμ=0,式(23)可以写成

Q(λ,d)=λ4-(c+γ)λ3+(cγ-α-υ)λ2+(γυ+αc)λ+αυ=

(λ2-cλ-υ)(λ2-γλ-α).

推论1βμ=0,暗示着β=0或者μ=0．如果β=0,可以得到f=0,由式(23),可以推出系统在平衡点E2处的稳定性．如果μ=0,可以得到g=0,由式(23)可推出系统在平衡点E0和E1处的稳定性．

在平衡点(f,g,0,0)处,(f,g)=(u*,v*),可得到

还可得到

对应的特征方程如下

(24)

注意

其中p(x)由式(19)可得．为了进一步简化,定义:

那么,式(24)可写成

(25)

定理2 1)如果c>0,σ<0,并且ρ+σ>0,则平衡点(f,g,0,0)是鞍点．

2)如果c<0,σ<0,并且X1<1+d

如果1+d>X2,则系统在平衡点(f,g,0,0)处是不稳定的．其中

(26)

(27)

证明 1) 由Hurwitz法则,可以得到平衡点(f,g,0,0)是鞍点．

2) 令ai(i=1,2,3,4)表示的是在方程组(25)中的多项式Q的系数.当c<0,σ<0,-ρ<σ<0,则a1>0,a2>0,a4>0．利用Hurwitz法则,求a3>0.假设X1<1+d

D(x)=-bρx2-(c2+b)σx+σ2

(28)

这就意味着D(1+d)>0,通过简单的计算,可得到a3>0．由Hurwitz法则,可以得到相应的结论．为了得到系统的稳定性,需要得到式(25)的纯虚根．令λ=ik是式(25)的一个根,则Q(ik,d)=0暗示着如下形式成立

分离实部和虚部,可得

(29)

(30)

[1] Aziz-Alaoui M A, Daher Okiye M. Boundedness and Global Stability for a Predator-Prey Model with Modified Leslie-Gower and Holling-Type II Schemes[J]. Lett Math Appl,2003,16: 1069-1075.

[2] Nindin A F, Aziz-Alaou M A, Cadivel M.Analysis of a predator-prey model with modified Leslie-Gower and Holling-type II schemes with time delay, Nonlinear Anal[J]. Real World Appl,2006,7:1104-1118.

[3] Xu R, Chaplain M A J. Persistence and global stability in a delayed Predator prey system with Michaelis-Menten type functional response[J]. Appl Math Comput, 2002,130: 441-455.

[4] Yafia R, Adnani F H. Talibi Limit cycle and numerical similations for small and large delays in a predator-prey model with modified Leslie-Gower and Holling-type II schemes[J]. Real World Applications,2008,9:2055-2067.

[5] Yafia R, Adnani F H, Talibi H. Stability of limit cycle in a predator-prey with modified Leslie-Gower and Holling-type II schemes with time delay[J]. Appl Math Sci,2007(3):119-131.

[6] Huang J,Lu G,Ruan S. Existence of travelling wave solutions in a diffuse predator prey model[J].Jour Math Biol, 2003,46: 132-152.

[7] Bierman M S, Fairbairn P J, Petty J S, et al. Changes over time in the spatiotemporal dynamics of cyclic populations of field voles[J]. Am Nat,2006,167: 583-590.

[责任编辑：李春红]

Existence of Periodic Traveling Waves Solutions in Predator Prey Model

XIONG Jun

(School of Mathematics, University of Lanzhou Jiaotong, Lanzhou Gansu 730070, China)

This paper deals with the qualitative analysis of the traveling waves solutions of a reaction diffusion model that refers to the competition between the predator and prey with modified.Leslie-Gower and Holling type II schemes.We establish sufficient condition for the asymptotic stability of the unique nontrivial positive steady state of the model by analyzing roots of the exponential polynomial characteristic equation

predator prey model; diffusion; stability; periodic traveling waves.

2017-02-13

熊军(1989-),男,甘肃临夏人,硕士研究生，研究方向为微分方程理论与应用动力系统． E-mail: 459584325@qq.com

O178

A

1671-6876(2017)02-0104-06