复合Linex对称损失下Rayleigh分布参数倒数的两种Bayes估计

罗 倩, 周菊玲

(新疆师范大学 数学科学学院, 新疆 乌鲁木齐 830017)

复合Linex对称损失下Rayleigh分布参数倒数的两种Bayes估计

罗 倩, 周菊玲

(新疆师范大学 数学科学学院, 新疆 乌鲁木齐 830017)

在复合Linex对称损失函数下,研究了Rayleigh分布位置参数已知的情况下,对尺度参数的倒数的Bayes估计和E-Bayes估计，随机模拟证明了其科学性.

复合Linex对称损失; Rayleigh分布; Bayes估计;E-Bayes估计

0 引言

Rayleigh分布在无线通讯、寿命分析中有着广泛的应用,很多国内外学者对Rayleigh的研究产生了浓厚的兴趣.陈志强在Linex损失下对Rayleigh分布参数倒数的Bayes一般形式进行了估计[1];邱燕等人在熵损失下对Rayleigh分布参数倒数的Bayes进行了估[2]计;余慧敏等人在Mlinex损失下对Rayleigh分布参数倒数完成了Bayes估计[3].张睿研究了复合Linex对称损失下,正态分布以及指数分布的参数估计并证明了其可容许性[4].

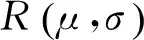
(1)

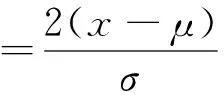
设随机变量X服从Rayleigh分布,X1,X2,…,Xn为来自总体,X的容量为n的简单随机样本,则其联合密度函数为

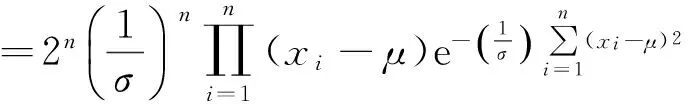
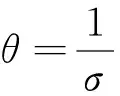
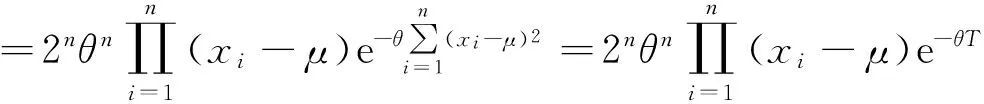
(2)

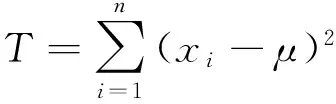
张睿提出了复合LINEX对称损失函数[4],表达式为

L(θ,δ)=La(θ,δ)+L-a(θ,δ)=e-a(θ-δ)+ea(θ-δ)-2,a>0

(3)

该损失函数是非负的,且该损失函数是关于δ的严格凸函数．

1 θ的Bayes估计

主要讨论尺度参数σ倒数的Bayes估计.θ的Bayes估计为

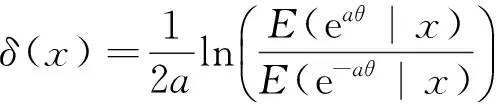
可由以下引理得到.

引理1[6]在复合LINEX对称损失函数(3)下,对任何的先验分布π(θ),θ的Bayes估计为

(4)

选取Γ(∂,β)为Rayleigh分布σ的倒数θ的先验分布，所以先验分布的密度函数为

(5)

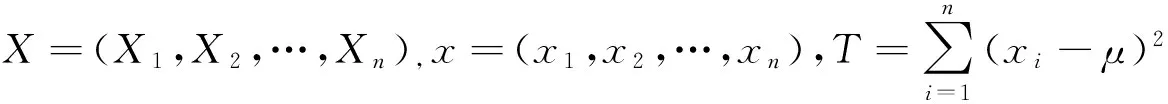
证明 由式(1)及先验分布有

(6)

所以参数θ的后验密度为

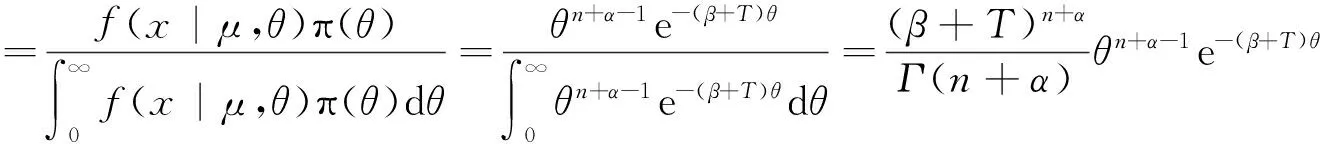
(7)

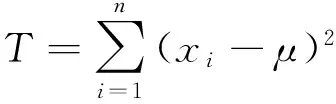
定理2 在复合对称损失函数(1)下,选取先验分布为Γ(α,β),Rayleigh分布尺度参数σ的倒数θ的Bayes估计为

(8)

证明 由引理1可得

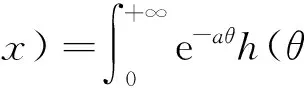
(9)

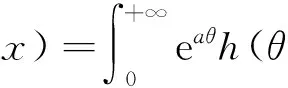
(10)

则尺度参数σ的倒数θ的Bayes估计为

(11)

2 复合Linexr损失函数下Rayleigh分布的E-Bayes估计

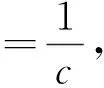
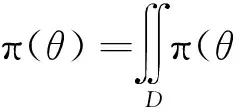
(12)

定义2[8]如果δ(α,β)是θ的参数Bayes估计含有超参数α和β且δ(α,β)是连续的，则称

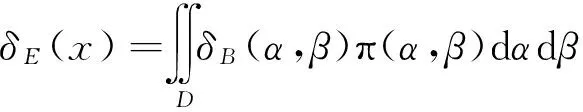
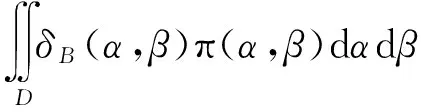
定理3 对Rayleigh分布，若参数的倒数θ的先验分布为Γ(α,β),在复合Linexr损失下，参数θ的E-Bayes的估计为

(13)

由定义2,有

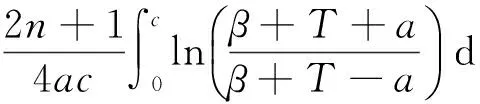
3 随机模拟

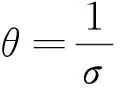
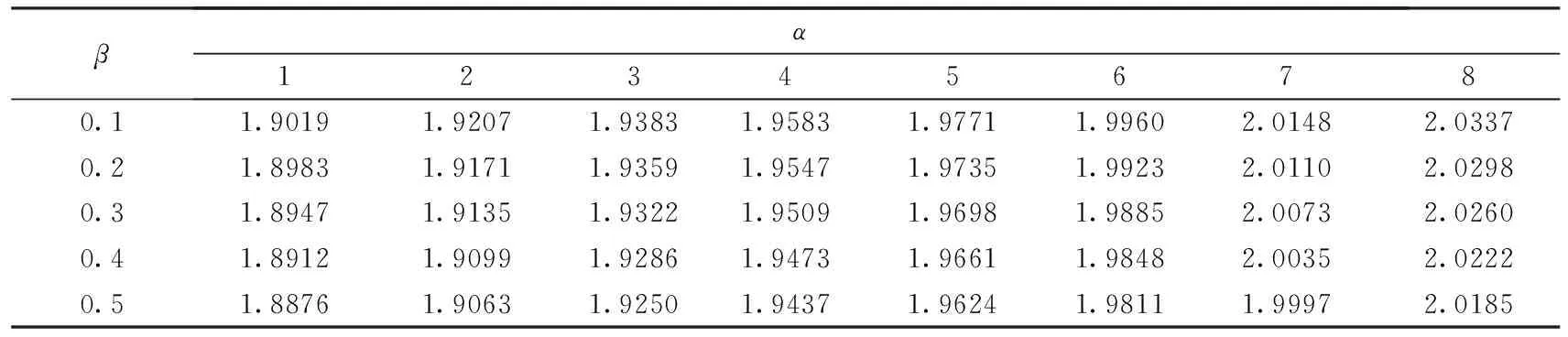
表1 δ(x)的估计值

由表1可以看出,δB(x)的估计值非常接近真实值θ=2,极差最大时是0.1461.对Rayleigh分布的Bayes估计也可以在不同的损失函数下实现,符合统计决策的稳健性,即我们的估计是科学合理的.对Rayleigh分布的E-Bayes估计形式更简单,可以实现数值模拟.

[1] 陈志强,韦程东,韦莹莹.Linex损失下Rayleigh分布尺度参数倒数的Bayes估计[J].广西科学，2007,14(4):362-364.

[2] 邱燕,韦程东,胡莎莎.熵损失下Rayleigh分布尺度参数倒数的Bayes估计[J].广西师范学院学报,2010,27(2)：39-43.

[3] 余慧敏,赵海清.Mlinex损失下Rayleigh分布尺度参数倒数的Bayes估计[J].岭南师范学院学报,2015,36(6)：14-16.

[4] 张睿.复合LINEX损失下的参数估计[D].大连:大连理工大学,2007.

[5] 韦程东.贝叶斯统计分析及其应用[M].北京:科学出版社,2015.

[6] 韦师.几种分布参数的E-Bayes估计及其应用[D].南宁:广西师范学院,2010.

[7] 韩明.参数的E-Bayes估计法及应用[J].数学的实践与认识,2004,34(9):97-106.

[8] 韩明.Pascal分布的参数估计[J].纯粹数学与应用数学,2006,22(4):510-514.

[责任编辑：李春红]

Two Bayes Estimation of the Reciprocal of Rayleigh Distribution Parameters under the Compound Linex Symmetric Loss

LUO Qian, ZHOU Ju-ling

(Department of Mathematical Sciences, Xinjiang Normal University, Urumqi Xinjiang 830017, China)

In this paper,the compound Linex symmetric loss function the Bayesian estimation andE-Bayes estimation of the reciprocal of the scale parameter was studied under the condition that the position parameter of the Rayleigh distribution is known,and the random simulation was carried out to prove its scientific nature.

compound linex symmetric loss; Rayleigh; Bayes estimation;E-Bayes estimation

2017-02-04

周菊玲(1968-),女,山东济南人，副教授,研究方向为概率论与数理统计. E-mail: 326815649@qq.com

O212.1

A

1671-6876(2017)02-0110-03