用积分算子定义的强星象函数和强凸象函数
陶玉琴, 杨 颖
(马鞍山师范高等专科学校 教师教育系, 安徽 马鞍山 243041)
用积分算子定义的强星象函数和强凸象函数
陶玉琴, 杨 颖
(马鞍山师范高等专科学校 教师教育系, 安徽 马鞍山 243041)

解析函数; 强星象函数; 强凸象函数; 星象函数; 凸象函数
0 引言及预备知识
设A(k)(k≥2)表示在U={z:|z|<1}解析,且具有形式
(1)
的全体函数组成的类,令A=A(2).用S*和K分别表示由A(k)中所有的星象函数和凸象函数组成的子类.
定义1 若φ(z)∈A(k),且满足
(2)
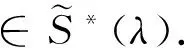
定义2 若φ(z)∈A(k),且满足
(3)

许多学者相继对强星象函数和强凸象函数进行了广泛地研究[1-6],本文将对上述两个函数类的充分条件进行讨论,为了证明主要结论,需要下面的两个引理.
引理1[1]设函数p(z)=1+c1z+c2z2+…在U内解析,且p(z)≠0,(z∈U),如果存在一个点z0∈U,使得
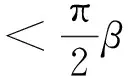
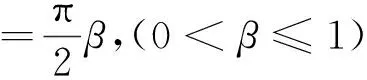
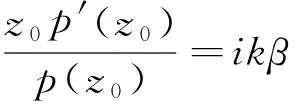
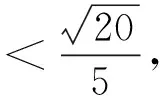
1 强星象函数和强凸象函数的充分条件
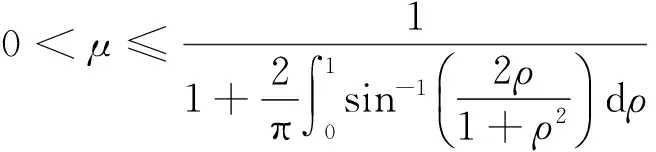
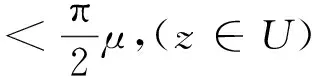
(4)
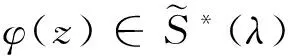

(5)
令 0=ρ0<ρ1<ρ2<…<ρn-1<ρn=r,ρm-ρm-1=δm,(m=1,2,…,n),
根据式(5)得到
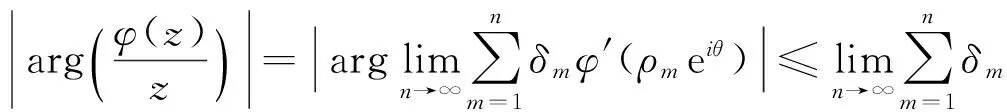
再根据条件(4)
φ′(z),
得到
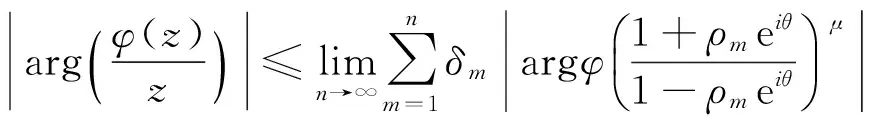

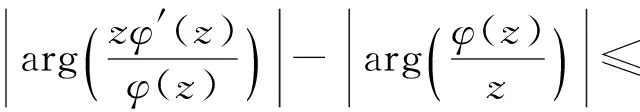
(6)
由条件(4)和(6)有
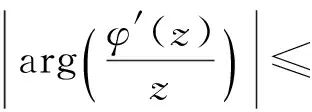
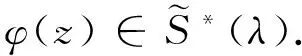
定理2 设0<λ≤1,若φ(z)∈A(k)(k≥2) 满足
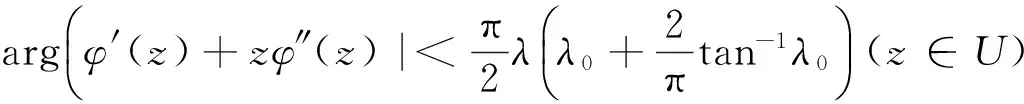
(7)
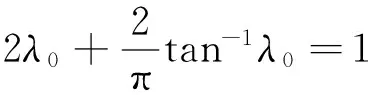



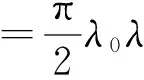
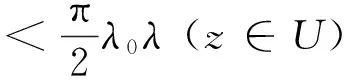
又因为

所以
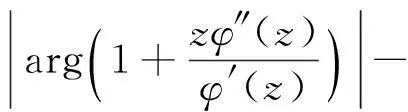
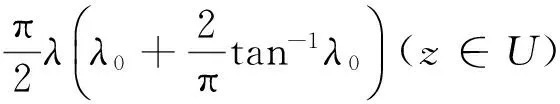
故
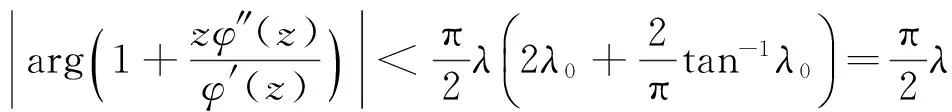
2 星象函数和凸象函数的充分条件
定理3 若φ(z)=z+akzk+…∈A(k)(k≥2)满足
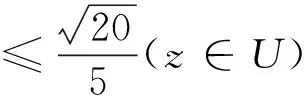
(8)
则φ(z)∈S*.
证明 根据式(8)得

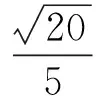
故

由引理2得到φ(z)∈S*.
定理4 若φ(z)=z+akzk+…∈A(k)(k≥2) 满足
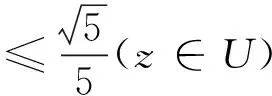
(9)
则φ(z)∈K.
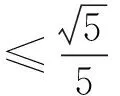
|(zφ′(z))′-1|=|φ′(z)+zφ″(z)-1|≤|φ′(z)-1|+|zφ″(z)|≤

由引理2得到zφ′(z)∈S*即φ(z)∈K.
[1] Nunokawa, M. On the order of strongly starlikeness of strongly convex functions[J]. Proc Jpn Acad Ser A Math Sci, 1993, 69(7):234-237.
[2] Mocanu, P T. Some starlikeness conditions for analytic functions[J]. Rev Roum Math Pures Appl, 1988,33(2): 117-124.
[3] Liu J L.Properties of certain subclass of multivalent func-tions defined by an integral operator[J]. Complex Varia-bles and Elliptic Equations,2009, 54(5): 471-483.
[4] Noor K I,Noor M A. On integral operators[J]. J Math Anal Appl,1999, 238(2): 341-352.
[5] 杨颖,陶玉琴.亚纯P叶星象函数的一类新子类的性质[J].牡丹江师范学院学报(自然科学版),2013,85(4):4-6.
[6] 陶玉琴,杨颖.用线性算子定义的一类亚纯多叶函数[J].阜阳师范学院学报(自然科学版),2014,31(2):12-14.
[责任编辑:李春红]
Strongly Star-like Function and Strongly Convex Function Defined with Integral Operator
TAO Yu-qin , YANG Ying
(Department of Teacher Education, Maanshan Teachers School, Maanshan Anhui 243041, China)
analytic function; strongly star-like function; strongly convex function; star-like function; convex function
2016-12-23
安徽省教育厅高校自然科学基金重点资助项目(KJ2016A694)
陶玉琴(1981-),女,安徽马鞍山人,副教授,硕士,研究方向为复分析. E-mail: 48654293@qq.com
O174.51
A
1671-6876(2017)02-0100-04

