基于光机械系统的质量探测器

马鹏程, 李晓薇, 詹佑邦

(淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)

基于光机械系统的质量探测器

马鹏程, 李晓薇, 詹佑邦

(淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)

光机械系统在精密测量方面的应用关键是基于纳米机械振子与高品质光学腔之间的强耦合．利用光学腔耦合纳米机械振子的同时通过库伦力耦合另外的一个带电纳米机械振子,并利用双模光力诱导透明等量子特性,发现第二个纳米机械振子随着附加质量的不断增加,两个透明窗口之间的距离(透射光频率之差)不断减小,根据此关系可精密测量附加在第二个纳米机械振子上微小物体质量．

光机械系统; 精密测量; 纳米机械振子; 光力诱导透明

0 引言

光学微腔是一种尺寸在微米量级或者亚微米量级并且具有高质量因子的光学谐振腔．目前光学微腔有许多种几何式样,常用的微腔有:平面微腔(Fabry-Perrot微腔)、回音壁模式微腔、光子晶体缺陷微腔等．腔光力学就是将光学微腔和力学结合起来的一门科学．腔光力学系统的基本物理图像是光学微腔的一个腔镜固定在一个微纳尺度机械振子上,通过光与镜子之间的辐射压,腔中的光场自由度和移动腔镜的机械运动自由度可以有效地耦合起来．

光机械系统在精密测量方面的应用主要是基于光与移动镜子的相互作用过程,在光机械系统中,纳米机械振子(Nanomechanical Resonator),简称NR,耦合与光学腔场使得光的辐射压力作用于纳米机械振子上,可以从腔的输出光谱中观测到纳米机械振子诱导的量子力学效应．目前,已有许多的理论及实验研究在此系统中,例如:光子阻塞,克尔效应,光力诱导透明效应(OMIT),量子信息转换,正则模分裂等．

光机械系统中的电磁诱导透明(简称光力诱导透明)是由Weis等人于2010年在实验上成功实现[1]．光力诱导透明效应是一种因为辐射压力而导致的透明现象,而且是最近几年里一个非常热门的研究方向,已有许多研究工作与此有关,例如:冷却纳米机械振子到量子基态[2],基于光机械系统的量子路由[3],精密测量耦合强度[4], 超慢与超快光传播及转换[5-6]等．另一方面,由于在原子系统内部存在双模电磁诱导透明(d-EIT),而光机械系统中也同样存在着与原子系统相似的能级结构及光与原子相互作用形式．因此目前也有多个理论方案讨论双光力诱导透明现象,例如:利用非线性晶体或量子比特耦合光机械系统实现双模光力诱导透明,在利用两个移动的镜子和一个固定的镜子构成环形腔模型基础上实现双模光力诱导透明．然而在以上所有的理论方案中,由于其固定的耦合强度,导致透射光的频率是固定无法调动的．而最近Ma P.C.等人提出了可调的双模光力诱导透明方案[7]．

本文主要利用光机械系统中可调的双光力诱导透明等量子特性精密测量附加在第二个纳米机械振子上的微小物质的质量．研究发现,随着第二个纳米机械振子附加质量的不断增加,两个透明窗口之间的距离(透射光频率之差)而不断减小,由此扫描出两个透明窗口出射光谱的频率之差后,便可根据此特性精密计算出附加在第二个纳米机械振子上微小物质的质量．

1 系统模型及哈密顿量

系统模型如图1,此系统总哈密顿为:

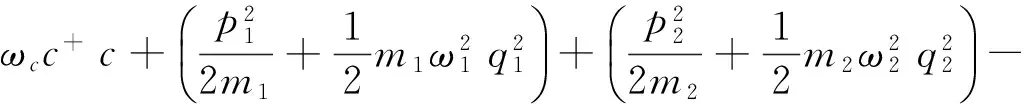
HC+iħεl(c+e-iωlt-h.c.)+iħ(c+εpe-iωpt-h.c.)

(1)

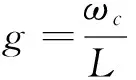
(2)

图1 系统模型示意图

图1中一个固定的镜子和一个移动的镜子,即纳米机械振子1(NR1)．NR1通过偏置电压V1带电并库伦耦合于腔外的另一个偏置电压为-V2的NR2．光学腔长为L并被两个驱动场驱动,其中一个为泵浦场εl其频率ωl,另一个为探测场εp．输出场用εl表示．q1和q2分别为NR1和NR2偏离其各自平衡位置的微小位移,r0为两个纳米振子平衡距离．其中r0为NR1和NR2之间的平衡距离,q1,q2分别为NR1和NR2偏离其各自平衡位置的微小位移,r0为两个纳米振子平衡距离．当r0≪q1,q2,利用二阶展开,第五项HC可以重新写为

(3)

其中,线性项可以吸收到平衡位置中,并重整化其NR1和NR2的频率,可简化为

HC=ħλq1q2

(4)

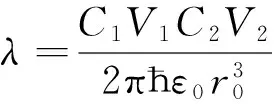
在泵浦光频率ωl的旋转坐标下,系统哈密顿可以重新表示为

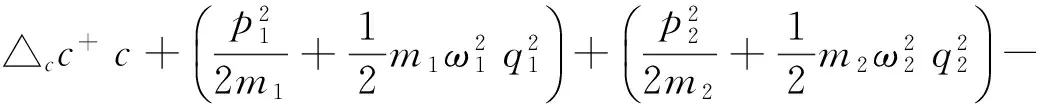
ħλq1q2+iħεl(c+-c)+iħ(c+εpe-iPt-h.c.)

(5)

其中,△c=ωc-ωl为泵浦场与腔场的失谐量,δ=ωp-ωl为探测场与泵浦场的失谐量．

考虑到光腔中光子数丢失及环境中的布朗噪声,则式(5)的动力学演化可以用如下非线性郎之万方程描述:

(6)

其中γ1和γ2分别为NR1和NR2衰减率．NR1(NR2) 的量子布朗噪声为ξ1(ξ2)并且其平均值为零．cin为真空输入噪声算符,其平均值也为零．在平均场近似下,〈Qc〉=〈Q〉〈c〉,其平均值可以表示为如下方程:

(7)

考虑到上式是一个非线性方程,其稳态在频域由多个不同的频率组分构成．由于在光力系统的稳态条件下,我们可以假设以上方程的稳态解为如下形式:

(8)

上述解中每一个都包含三个项Os,O+,O-(其中O∈{q1,p1,q1,p1,c}),它们对应的原始频率分别为ωl,ωp,和2ωl-ωp．在Os≫O±条件下,式(8)可以将余下的两个频率组分O±当成扰动处理．将式(8)代入式(7)中,并忽略二阶小量,可以求得系统的稳态平均值:

(9)

其中,△=△c-gq1s,扰动输出为

(10)

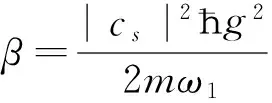
利用腔场的输入输出关

εout(t)+εpe-iδt+εl=2κ〈c〉

(11)

(12)

可以得到

εout+=2κc+-1

(13)

上式可以利用零差探测技术测量得到．输出光谱εout+与探测场频率ωp具有相同的频率．我们定义

εT=εout++1=2κc+

(14)

其对应的实数Re[εT]和虚数部分Im[εT]分别代表此光机械系统的吸收和色散．

2 精密测量附加在NR2上的微小物质质量

为表示数值模拟的实验可行性,本文采用文献[8]中的实验参数,如图2所示,输出场的吸收谱Re[εT]和Im[εT]色散谱随x/ω1=(δ-ω1)/ω1变化的函数关系,其中参数选择:λl=1 064 nm,L=25 mm,ω1=ω2=2π×947×103Hz,质量因子Q1=ω1/γ1(=Q2=ω2/γ2)=6 700,m1=m2=145 pg,κ=2π×215×103Hz,Pl=2 mW,λ=8×1035Hz/m2[8]．从图2中能够看出,在一定的腔场耦合强度下,系统的透射光谱中出现两个明显的透明窗口．

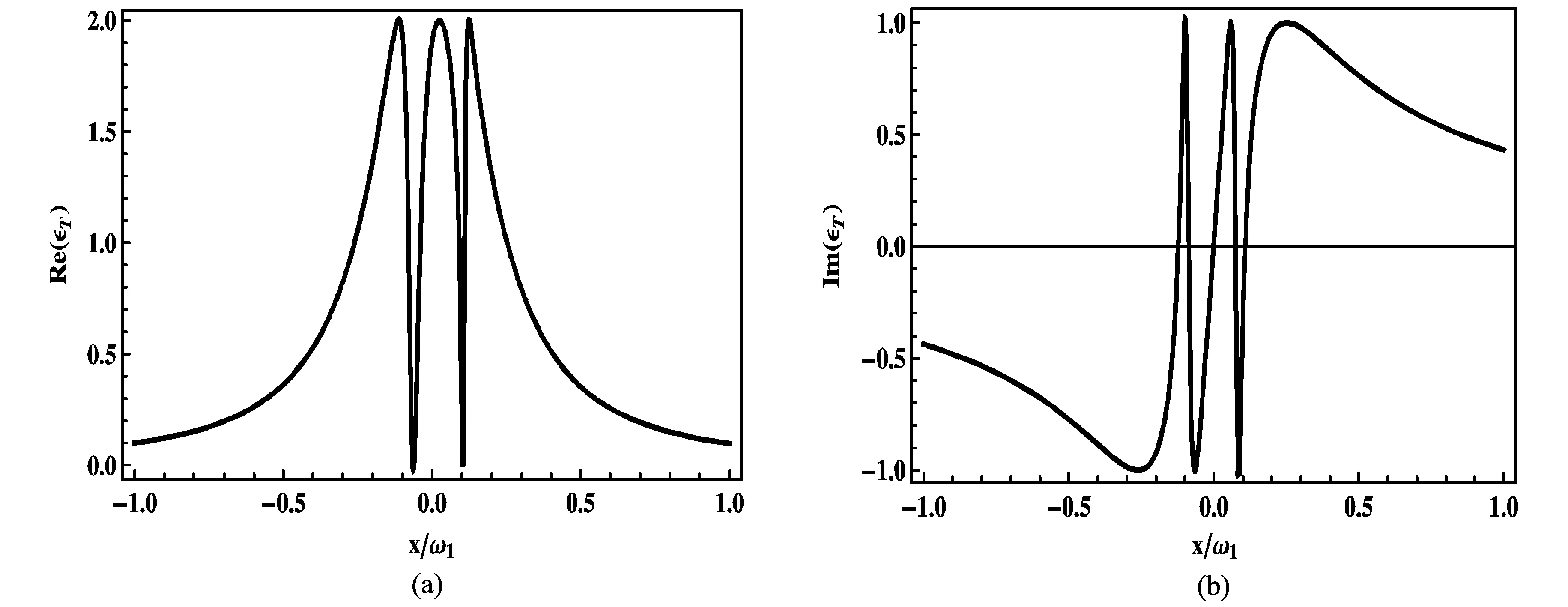
图2 当存在一定的库伦耦合时(a)输出场的吸收谱Re[εT]和(b)色散谱Im[εT]随x/ω1变化的函数关系

光力诱导透明源于光学膜和机械模之间的辐射压力,当同时存在泵浦场和探测场,便会产生频率差为δ=ωp-ωl的拍频,当此频率差和NR1的频率ω1接近,机械模由于共振相干作用使得泵浦场而发生斯托克斯过程和反斯托克斯过程,如果此系统工作在红边界范围κ≪ω1,跟腔场大程度的失谐而导致斯托克斯过程被压制,此时只有反斯托克斯过程ωp=ωl+ω1在腔内产生,由于此频率的光与腔场的频率接近而发生干涉相消使得探测光透明窗口的出现．由于量子干涉导致其透明窗口的出现,故非常敏感与相位失谐;纳米振子NR1和NR2之间的耦合不仅增加了第四个能级,而且打破了量子干涉平衡,从而使得单个透明窗口劈裂成两个透明窗口．

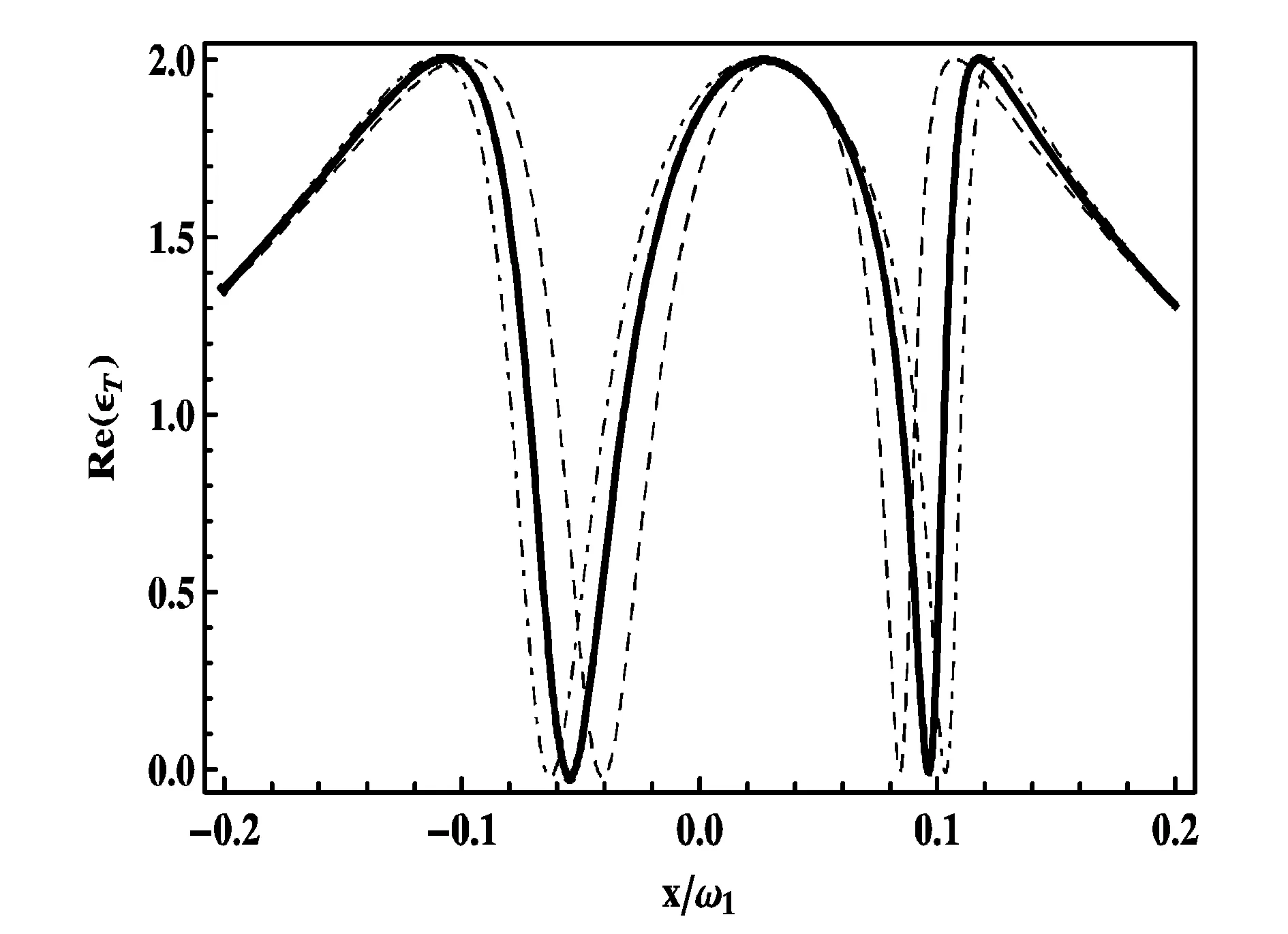
图3 在NR2附加不同质量△m 的情况下吸收谱Re[εT]随着x/ω1函数变化关系图

为了更深入的研究双模光力诱导透明的特性,我们画出在NR2附加不同质量△m的情况下吸收谱Re[εT]随着x/ω1变化关系图(如图3)．图3中，△m=0 pg时为短虚线,△m=40 pg时为实线,△m=85 pg时为长虚线.从图3中可以发现,随着NR2附加质量△m的增大,两透明窗口的距离(透射光频率之差)越来越小．

图3中两个吸收最小值点之间的距离可以通过如下方程计算得出

(15)

(16)

其中,x+和x-是吸收光谱中的两个最小值位置,因此两吸收谱之间的距离d=|x+-x-|,在一定范围内两吸收谱之间的距离随△m变化大致成线性关系．因此,只要精确测出距离d,便可以精确的计算出附加在NR2质量△m的大小．

3 结论

利用光机械系统中可调的双光力诱导透明等量子特性精密测量附加在第二个纳米机械振子上的微小物质的质量．研究发现,随着第二个纳米机械振子附加质量的不断增加,两个透明窗口之间的距离(透射光频率之差)而不断减小,由此扫描出两个透明窗口出射光谱的频率之差后,便可根据此特性精密计算出附加在第二个纳米机械振子上微小物质的质量．

[1] Weis S, Riviere R, Deleglise S, et al. Optomechanically Induced Transparency[J].Science, 2010, 330(6010): 1520-1523.

[2] Genes C, Vitali D, Tombesi P, et al. Ground-state cooling of a micromechanical oscillator: Comparing cold damping and cavity-assisted cooling schemes[J]. Phys Rev A, 2008, 77: 033804.

[3] Agarwal G S,Huang S. Optomechanical systems as single-photon routers[J]. Phys Rev A, 2012,85: 021801.

[4] Li J J, Zhu K D. A scheme for measuring vibrational frequency and coupling strength in a coupled nanomechanical resonator-quantum dot system[J]. Appl Phys Lett, 2009, 94: 063116.

[5] Zhou X, Hocke F, Schliesser A, et al. Slowing, advancing and switching of microwave signals using circuit nanoelectromechanics[J]. Nat Phys, 2013(9): 179-184.

[6] Ma P C, Xiao Y, Yu Y F, et al. Microwave field controlled slow and fast light with a coupled system consisting of a nanomechanical resonator and a Cooper-pair box[J]. Opt Express, 2014, 22(3): 3621-3628.

[7] Ma P C, Zhang J Q, Xiao Y, et al. Tunable double optomechanically induced transparency in an optomechanical system[J]. Phys Rev A, 2014, 90: 043825.

[8] Hill J T, Safavi-Naeini A H, Chan J, et al. Coherent optical wavelength conversion via cavity optomechanicas[J]. Nat Commun, 2012(3): 1196.

[责任编辑：蒋海龙]

Precision Mass Sensing based on the Opto-mechanical Systems

MA Peng-chen, LI Xiao-wei, ZHANG You-bang

(School of Physics and Electronic Engineering, Huaiyin Normal University, Huaian Jiangsu 223300, China)

Precision measurement of opto-mechanical systems is based on the strong coupling between nano-mechanical resonator and high-quality opto-cavity. By using the two-mode opto-mechanics induced transparency beased on the system, we find the corresponding relation between the frequencies of transmission lights and the added mass of the NR2. Then we can obtain the precision mass.

opto-mechanical systems; recision measurement; ano-mechanical resonator; pto-mechanical induced transparency

2016-06-26

国家自然科学基金资助项目(11547023)

马鹏程(1979-),男,山东临沂人,讲师,博士,研究方向为量子光学与量子信息理论． E-mail: mapch95812@163.com

O431.2

A

1671-6876(2017)02-0126-05