量子力学中坐标平移算子的性质及其应用

郁华玲

(淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)

量子力学中坐标平移算子的性质及其应用

郁华玲

(淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)

在古典力学到量子力学的范式转变过程中,平移算子具有重要的代表性.本文从古典的坐标平移概念出发引入平移算子,利用量子力学的基本原理推导出无限小平移算子以及有限位移平移算子的表达形式,进而对其性质和运用进行了探讨.研究表明厄密的动量算子产生了反厄密的幺正平移算子,也就是说动量算子操纵了坐标的平移过程,同时坐标的一对平移算子也是坐标本征矢一对阶梯算子.将平移算子运用到谐振子上,较好地求解出了其相干态.

量子力学; 平移算子; 阶梯算子; 相干态

0 引言

1900年Max Planck提出的能量量子化理论敲开了量子力学的大门[1],此后古典力学和量子力学之间的关系一直是人们研究和讨论的热门课题.古典力学适用于低速宏观的物体,其运动状态由确定的相轨迹来描述，而微观粒子的运动规律遵循量子力学原理.量子力学抛弃了古典力学运动轨迹的概念,提出了几条基本假设[2-3]: 1) 微观粒子的运动状态用几率波态函数来描述,量子态满足叠加原理; 2) 力学量一次量子化成算子,测量值一定是该算子本征方程求得的本征值; 3) 两算子的乘法交换关系及量子化条件; 4) 量子态满足运动方程.在这4条公设下推演出了量子力学一系列的原理和定律.而所有这些原理和结论都还在接受着实践的检验.

在从古典力学到量子力学的范式转变中,算子扮演着重要的角色.力学量对应的线性厄米算子是量子力学数学体系的核心.厄米算子的性质及本征方程的求解结果直接决定了其对应力学量的测量结果.在量子力学中,算子与算子之间乘积的不可交换性称之为对易关系,对易关系决定了它们对应力学量之间的不确定关系,这一关系可以说是量子力学的心脏.在量子力学中有一类著名的算子叫阶梯算子,它们不和某个力学量对应,不是厄米算子,但在量子力学的计算过程中阶梯算子是一个非常有用的工具,常使对一些重要模型体系的理解豁然开朗,例如谐振子的一对阶梯算子形象的理解为粒子数的产生和湮灭算子.这些阶梯子算子经常使得量子力学的计算别开生面[4-6].但在一般的量子力学教材中有的不提及阶梯算子,只介绍了谐振子的产生湮灭算子[7],有的介绍了阶梯算子,但也最多只介绍三对阶梯算子:角动量阶梯算子;谐振子阶梯算子;自旋阶梯算子[8].本文从古典的坐标平移概念出发定义平移算子,利用量子力学的基本原理推演出平移算子所具有的各种性质,从而给出量子力学中坐标本征矢的一对阶梯算子.

1 平移算子的定义

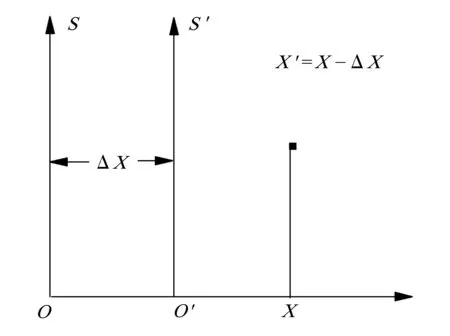
图1 坐标系平移示意图

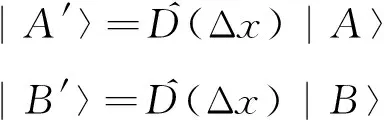
(1)

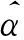
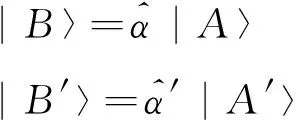
(2)

由式(1)(2)可得:

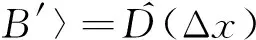
(3)

由式(2)(3)比较可得:

(4)

式(4)表达了算子在平移变化下的表示[9-10].

2 平移算子的性质

2.1 平移算子的幺正性

因为态矢量在平移变换下内积不变,所以:

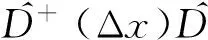
(5)

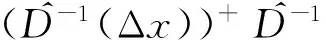
(6)

由式(5)(6)可得:

(7)

2.2 无限小位移算子的反厄密性

考虑无限小坐标平移变换的情况,即Δx→0的极限情况.令:

(8)

得到无限小位移生成算子:

(9)

将式(8)代入式(7)可得:

(10)

由式(10)得到:

(11)

式(11)表示了无限小位移算子的反厄密性质.

2.3 动量算子操纵平移过程

(12)

将式(8)代入式(12),再利用式(11)得:

(13)

因为x′=x-Δx,所以有:

(14)

量子力学中坐标和动量算子的交换关系式为:

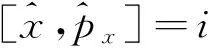
(15)

比较式(14)(15)可得:

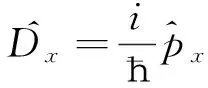
(16)

将上式代入式(8)得到:

(17)

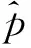
由式(17)可以得到动量算子和平移算子是对易的,也就是说动量算子在平移变换下保持不变,所以动量在平移操作下是守恒量,平移算子的本征态也是动量算子的本征态.

2.4 有限平移算子的阶梯性

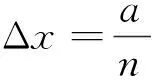
(18)

将式(16)(17)两式代入上式得到:

(19)

利用对易关系[10]:

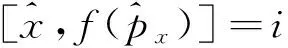
(20)

并且把式(19)代入式(18)可以得到:

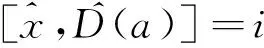
(21)

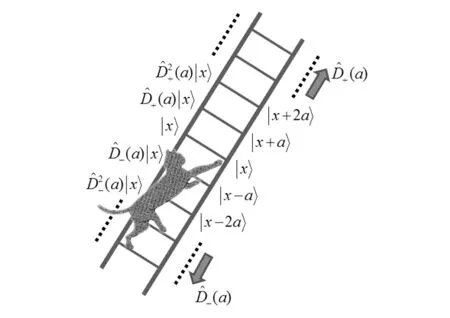
图2 坐标本征矢的一对 梯子算子示意图

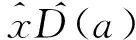
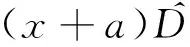
(22)

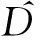
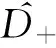
(23)

同理有

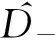
(24)

3 利用平移算子求解谐振子的相干态

对于谐振子来说,定义了一对能量本征态的阶梯算子:

(25)

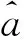
(26)

(27)

式(27)两边作用到|z〉态上:

(28)

所以

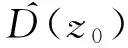
(29)

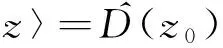
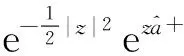
(30)

此相干态是谐振子所有能量本征态的相干叠加.

4 小结

本文从古典力学出发引入坐标平移算子,利用量子力学基本原理推导出其表达形式,并进一步分析了其幺正性、反厄密性、阶梯性等特点.同时利用谐振子的平移算子较好地求解出了其相干态.

[1] Plank M. On the Theory of the Energy Distribution Law of the Normal Spectrum[J]. Verh Dtsch Phys Ges，1900(2):237-245.

[2] Dirac P A M. The Principles of Quantum Mechanics[M]. 北京: 科学出版社, 2008.

[3] 张永德. 量子力学[M]. 北京: 科学出版社,2008.

[4] 王曼英, 王永昌. 如何构造阶梯算符[J].大学物理,1993(12): 24-25.

[5] 游佩林, 黄湘友.从体系计算中讨论海森伯不确定关系[J].物理,2012,41:811-815.

[6] 濮振文, 卓光辉. 经典振子和量子振子的对应关系[J].物理,1986,15:579-583.

[7] 周世勋. 量子力学教程[M]. 北京: 高等教育出版社,2009.

[8] Griffiths D J. Introduction to Quantum Mechanics[M]. New York: Pearson Education International, 2005:131-171.

[9] 喀兴林. 高等量子力学[M]. 北京:高等教育出版社,2001:247-256.

[10] Sakurai J J. Modern Quantum Mechanics[M]. California: Addision-Wesley Publishing Company, 1994: 41-50.

[责任编辑：蒋海龙]

The Properties and Applications of Coordinate Translation Operators in the Quantum Mechanics

YU Hua-ling

(School of Physics and Electronic Electrical Engineering, Huaiyin Normal University, Huaian Jiangsu 223300, China)

Translation operators are typical and unique in the progress of paradigm shifting from classical mechanics to quantum mechanics. Translation operators are defined in the classical mechanics, and then the expressions for both infinitesimal and finite translation are derived by using the basic principle of quantum mechanics. It is shown that the translation operator is unitary and anti-Hermitian and ladder for the eigenvectors of coordinate. The momentum operator controls the progress of coordinate translation. The coherent states of harmonic oscillator is investigated skillfully by translation operators.

quantum mechanics; translation operators; ladder operators; coherent states

2017-03-08

江苏省自然科学基金资助项目(BK20140450); 淮安市科技计划项目(HAG2014043)

郁华玲(1975-), 女,江苏沭阳人,副教授,博士,主要从事凝聚态理论的研究. E-mail: hlyu-phys@126.com

O413

A

1671-6876(2017)02-0131-04