圆锥曲线焦点三角形的一个有趣性质

广东省深圳市盐田高级中学 (518083) 罗 诚

圆锥曲线焦点三角形的一个有趣性质

广东省深圳市盐田高级中学 (518083) 罗 诚

最近某地有一道解析几何试题如下：

A．|OB|=e|OA|

B．|OA|=e|OB|

C．|OB|=|OA|

D．|OA|与|OB|关系不确定

笔者探究上述问题的解法时，发现圆锥曲线焦点三角形有类似的一个有趣的性质，现将结果与大家分享.

图1

证明:如图1，设椭圆的焦距为2c,直线PF1,F1B的交点为Q，P(x0,y0).|PF1|=r1,|PF2|=r2.则由椭圆的焦半径公式得r1=a+ex0,r2=a-ex0(其中e为椭圆的离心率).

因为⊙I是△PF1F2的内切圆，所以|PF1|=|PQ|,B为F1Q的中点，∴OB,即，由三角形内心坐标公式得

|OA|=|xI|=e|x0|.所以|OA|=|OB|，命题1成立.

图2

证明可仿命题1，此略.

图3

命题3 已知抛物线y2=2px(p>0)的焦点为F，F′是准线与x轴的交点，O为抛物线的顶点，P是抛物线上的一点，ΔPFF′的内切圆的圆心为I，且⊙I与x轴相切于点A，过F′作直线PI的垂线，垂足为B，则|OA|=|OB|.

证明:如图3，设直线PF,F′B的交点为Q，P(x0,y0)，|PF|=r1,|PF′|=r2.则由抛物线的定义

因为⊙I是ΔPFF′的内切圆，所以|PF′|=

|PQ|,B为F′Q的中点，∴OB,即

由三角形内心坐标公式得

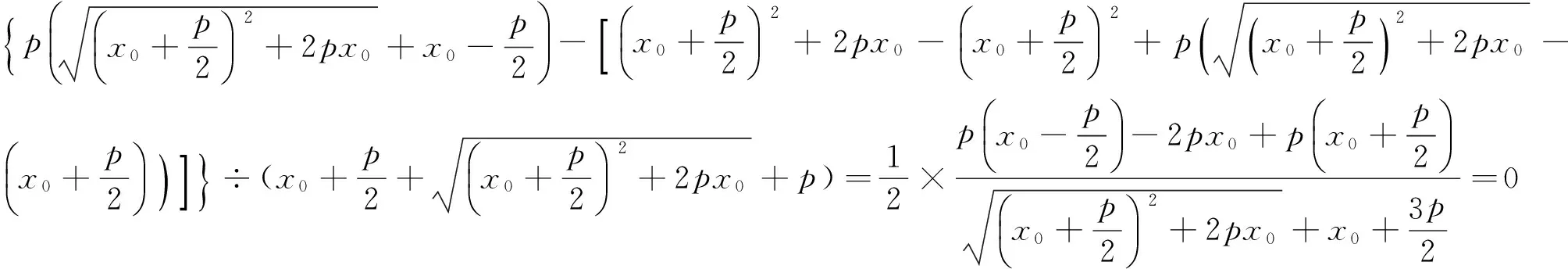
即|OB|=xI.又|OA|=xI.

所以|OA|=|OB|.至此，命题得证.