玩转函数:一道二次函数问题引发的思考
江苏省苏州实验中学 (215000) 董逸婷
玩转函数:一道二次函数问题引发的思考
江苏省苏州实验中学 (215000) 董逸婷
函数是高中数学学习的开始,它是数学思想的基础,也是高中数学的难点,同时又是历年高考的宠儿.函数概念的产生标志着数学思想方法的改变,从常量数学转变成了变量数学.在整个高中数学教学过程中,所占的比重和比值都是不容忽视的,它的难点主要表现在它的抽象性上,需要学生不断的利用发散性思维的方式来推导出函数的运动轨迹图像,对于函数的解题思路的把握,成为了攻克这一难关的金钥匙,成为解题的关键.图像是函数的灵魂,但是很多学生对于函数的理解是分离的,不能有效地进行数形结合,从而从高一开始就成为了函数的学困生,纠缠整个高中阶段.
一、高中数学函数解题思路现状
从初中到高中,学生的思维是由具体形象思维慢慢过渡到形式逻辑思维的.而在转变与发展的过程中,高一阶段,首先遇到了抽象的函数概念,从而大部分学生对于函数的认识,停留在表层抽象概念,并没有理解两个数集在对应法则下的一一对应关系.函数的学习处于低层次被动地接受基本知识点,缺乏高层次的思维.函数解题也只是停留在局部的、分隔的知识点上,而不能从整体上把握函数图像,研究函数性质,解决函数问题.如何提高教学质量、有效提升学生函数能力,成为了一个亟待解决的问题.
二、高中函数解题思路多元化的重要性
数学是抽象的学科,学生在学习数学时主要是通过解题方式掌握数学知识和实际运用.然而我们在学习过程中,常常会通过一种方法得到答案,却不能清晰了解该题思路,导致我们对相应知识的思考一直处在相对保守且封闭的空间内.同时,教师教学或者教材内容所展现的解题方式常常禁锢其中,严重影响了思维发散.因此为了使学生能够更加完善的掌握函数知识,在面对题目或其他事物时,能够有发散性的思维、多途径的解决问题的手段,我们在函数学习中可以尝试设计一题多解的专题课堂,全方位、多角度的研究问题,以帮助学生灵活的玩转函数.
三、高中数学函数解题思路多元化举例
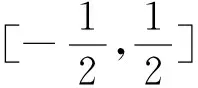
分析:本题的关键是求出集合A.
条件:函数f(x)=x(1+a|x|).
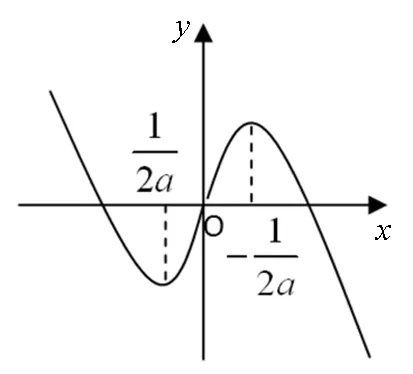
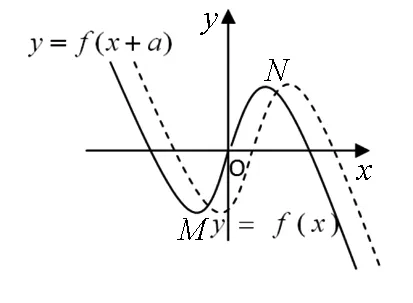
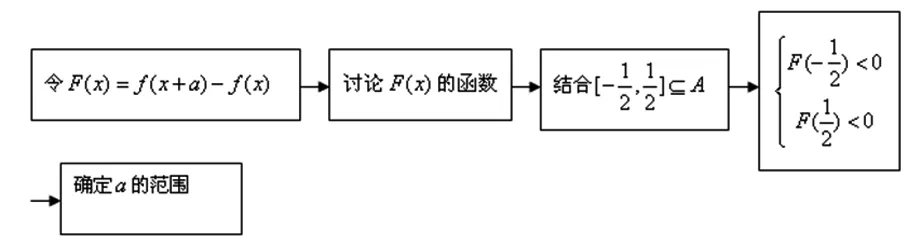
目标:解不等式f(x+a) 目标差:参数a的取值范围是本题下手处理的关键,无论是利用代数法还是数形结合,难点都是关于a的含参讨论.首先找到a的局限性,将是缩小目标差的第一步. 图1 思路一:直接分类求解不等式 方案设计: 解得-1 在解该含参不等式时,不等式对应的方程的根是代数式,需要与原始范围比较大小,从而合并解集. 思路一需要学生有很好的数学功底,相应运算量也比较大. 思路二:利用函数性质解不等式 方案设计: 解析:由思路一知-1 图2 在利用单调性解题时,首先遇到的讨论是两个自变量是否在同一单调区间上. 第②③种情况当自变量值不在同一单调区间上时,用函数对称性转移至同一单调区间上比较函数值大小.在讨论中注意参数的范围,合理缩小讨论范围,简化问题. 思路三:利用函数图像解不等式 方案设计: 图3 解析:由a<0,将函数y=f(x)的图像向右平移-a个单位长度,得函数y=f(x+a)的图像如图3,它与函数y=f(x)的图像的两交点M,N的横坐标是方程f(x)=f(x+a)的解,即x(1+a|x|)=(x+a)(1+a|x+a|).问题转化为求解绝对值方程,得到两函数零点,利用数形结合,观察出不等式解集. 思路三利用函数图像求解这类比较复杂的含参数不等式,数形结合的优势跃然纸上.著名数学家华罗庚说过:“在解题中千万不要得‘意’而忘‘形’”,数形结合的思想就是“数”与“形”之间的相互对应和相互转化的思想,利用数形结合思想与方法来分析解决问题,可使一些复杂问题简单化、抽象问题直观化,从而化难为易,化繁为简,达到顺利破解问题. 思路四:利用函数与不等式关系解 方案设计: 思路四把不等式转化为对应函数,借用函数性质与图像结合解含参不等式,也是一种妙法,可以避免复杂的分类讨论. 对比上述四种解法,分别从代数角度、图像角度、动态分析角度、新函数构造角度入手,对同一问题进行解决,需要学生有扎实的函数功底、灵活的解题手法、高屋建瓴的解题思路.如果在教学过程中,我们可以留出一点时间,对有些问题进行这样的深度挖掘,相信可以很好的帮助学生提升函数分析能力. 玩转函数可以有效的帮助学生形成数学问题思考的主动性和创新性,让学生在面对一道函数题时能够以举一反三的思维方法进行解题.当学生面对问题可以有多元化的解题思路时,函数这个难点自然不攻自破.


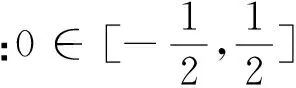
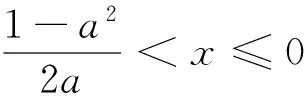

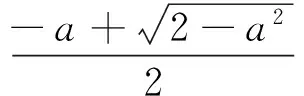


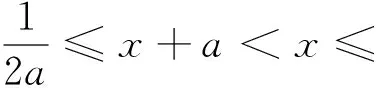

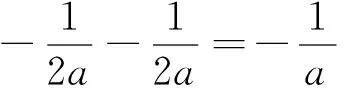
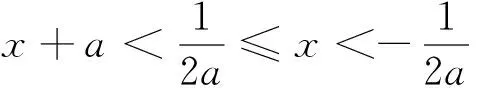


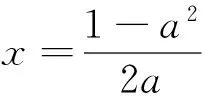
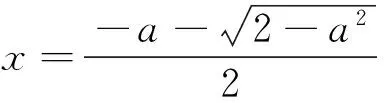
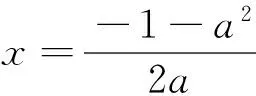
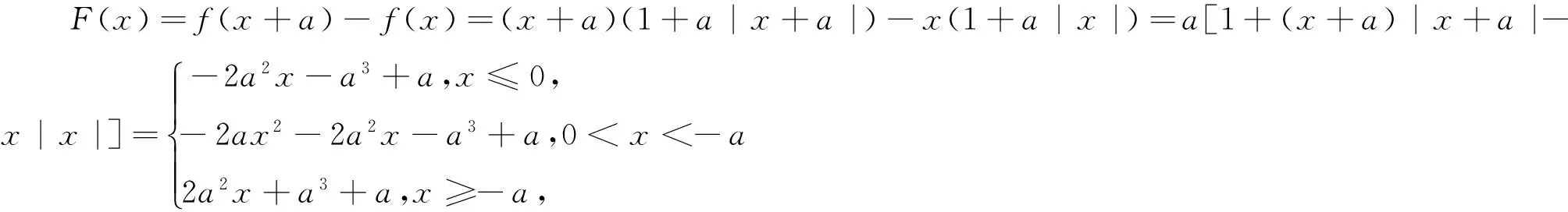
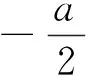



三、结束语

