基于双阈值LSTR的我国菲利普斯曲线非线性特征的实证研究

李冠超 郭 凯 李 政

一、引言

近几年我国经济增速放缓，物价水平持续走低。在新常态下，我国通胀水平的动态变化受到通胀预期等多种因素影响，货币政策操作对于通胀变动的反应呈现出非对称性。菲利普斯曲线作为刻画通胀与产出之间关系的曲线，其所包含的经济关系是货币政策传导机制中的关键一环。在复杂的经济运行态势以及宏观经济政策的背景下，迫切需要探求我国菲利普斯曲线的具体形式。正是基于此，本文将结合我国的实际经济，利用平滑转移回归模型对我国菲利普斯曲线的非线性特征进行实证研究，并对我国的宏观经济政策提出相应的政策建议。

二、文献综述

尽管关于菲利普斯曲线的理论和实证研究不断完善，但现有研究在拟合现实经济运行情况时仍存在局限性，其重要原因在于传统的菲利普斯曲线大都基于线性或对称性的假设，特别当通胀动态发生结构性变化时，基于线性和对称性假设的菲利普斯曲线的结论建议就备受质疑。在此背景下，国外不少经济学家开始修正菲利普斯曲线的线性假设，试图从非线性的角度来对菲利普斯曲线进行研究。

菲利普斯曲线最初由Phillips（1958）［1］提出，当失业率极低时，通货膨胀率急速上升，当失业率较高时，通货膨胀率会出现负值，且这一过程的变化速率是变化的，即最初的 “失业－工资”菲利普斯曲线是非线性的。此后的Lipsey（1960）［2］也认为，工资的线性变动所带来失业率或通货膨胀率并不是线性的。现有的新凯恩斯理论的价格行为模型也开始采用非线性形式的分析方法，例如，在新凯恩斯的生产能力约束模型中，当总需求对价格产生冲击时，价格水平所进行的调整就是凸性的。实证分析方面，国外文献也开始侧重非线性菲利普斯曲线的研究。Clark等（1996）［3］利用美国30年间的相关数据对比了线性和非线性菲利普斯曲线，结果检验了非线性菲利普斯曲线的存在； Filardo（1998）［4］和 Dolado（2004）［5］的实证结论虽截然相反，但都认为菲利普斯曲线会随着经济对趋势的偏离而在凸性与凹性之间进行转换，即菲利普斯曲线存在非线性特征。

在非线性模型的选择上，有的文献采用运用条件自回归模型研究通货膨胀波动，如Engle（1983）［6］；有的文献采用马尔科夫机制转移模型研究通胀与经济增长的非线性特征，如 Hamilton（1989）［7］。 现有文献大多采用由 Granger和 Terasvira（1993）［9］提出的STR（Smooth Transition Regression）模型，由于STR模型具有平滑转换的特性，因而也应用于非线性菲利普斯曲线及其货币政策效应的研究，其代表性的文献有 Skalin 和 Terasvirta（1999）［9］、 Bruinshoofd 和 Can⁃delon（2004）［10］等。

国内关于菲利普斯曲线的传统研究侧重两个方面：一是对传统菲利普斯曲线在我国的适用性进行检验，这些研究见于早期文献，如陈学彬（1996）［11］、刘树成（1997）［12］、 范从来（2000）［13］、 闵正良（2002）［14］等；二是检验我国的短期和长期菲利普斯曲线，如张焕明（2003）［15］、 徐秋慧和李秀玉（2008）［16］、 杨继生（2009）［17］、 贺根庆和王伟（2013）［18］等。 张焕明（2003）［15］认为我国菲利普斯曲线在短期内呈直线，而长期内向右下方倾斜。近期研究开始转向我国菲利普斯曲线的具体形式，研究视角侧重于对通胀预期形式的判定、对通胀惯性的解释以及通货膨胀的非线性、非对称性等方面，并因此更为侧重于对混合菲利普斯曲线以及非线性菲利普斯曲线的扩展和修正。在混合菲利普斯曲线的研究方面，杨继生（2009）［17］认为我国菲利普斯曲线具有短期混合菲利普斯曲线的形式；在非线性菲利普斯曲线的研究方面，如刘金全等（2006）［19］、王少平和彭方平（2006）［20］、 陈建宝和乔宁宁（2013）［21］等。 刘金全等（2006）［19］采用包含区制转移的状态空间模型对我国的通货膨胀动态进行实证研究，认为我国菲利普斯曲线具有长期菲利普斯曲线的特征。王少平和彭方平（2006）［20］利用ESTR模型对我国通货膨胀的非线性特征进行了实证研究，结论表明我国通货膨胀动态以及通货膨胀与通货紧缩之间的转换都呈现出明显的非线性特征。许冰和章上峰（2008）［22］认为我国菲利普斯曲线的非线性可以被描述为三次多项式的形式。孙燕（2012）［23］则利用扩展的 LSTR模型进行实证分析，表明我国的产出缺口与通货膨胀之间存在显著的非线性。

现有研究认为我国菲利普斯曲线具有混合预期特征和非线性特征，本文研究则将这两种特征结合起来，这也是本文研究的创新之处，具体体现在两个方面：（1）采用高阶滞后的混合菲利普斯曲线形式对我国菲利普斯曲线的非线性特征进行实证研究，因而能较全面地涵盖影响我国通货膨胀的预期因素，并很好地拟合了我国的通货膨胀动态。（2）采用双二阶逻辑平滑转移机制模型对我国菲利普斯曲线的非线性特征进行实证研究。二阶逻辑平滑转移函数意味着非线性转换过程当中应具有双阈值，这对于我国频繁变动的菲利普斯曲线形式具有更高的解释力。

本文结构安排如下：第三部分简要介绍了所采用的平滑转移回归模型，并对相关指标变量的含义与计算依据做了说明。第四部分首先对指标变量进行数据平稳性检验，其次对平滑转移回归模型进行检验和选择，最后对基于双阈值逻辑平滑转移机制的我国菲利普斯曲线的非线性特征进行实证分析。第五部分为主要结论总结和建议。

三、计量模型与指标变量

（一）计量模型设定：平滑转移回归模型（STR）

本文所运用的平滑转移回归模型（STR）采用STR模型的一般表达式，形式如下：

其中：yt为被解释变量；xt＝（1，x～′t）′为解释变量向量；x～t＝（y1，…，yt－k；z1t，…，zmt）′；p＝k＋m；参数φ1＝（φ1，0，φ1，1，…，φ1，p）′与φ2＝（φ2，0，φ2，1，…，φ2，p）′分别表示模型线性部分与非线性部分的参数向量；εt为独立同分布的随机扰动项。

转移函数G（γ，c；st）反映了机制转换的过程，是可观测变量st的连续函数，值域为 ［0，1］。其中，可观测变量st为阈值变量，它可以是解释变量向量中任一元素或是其滞后期，也可以是多个元素的线性组合，甚至可以是一个确定的时间趋势。转移函数会随着st的变动在其0～1之间平滑转换。参数γ为转移速度，用于衡量平滑转移的平滑程度，反映了由状态0转变为状态1的速度。参数c为阈值，表示机制转换发生的转折点。在c处实现平滑的机制转移的方式则取决于转移函数的具体形式。

根据转移函数形式的不同，STR模型分为逻辑平滑转移模型（LSTR）和指数平滑转移模型（ESTR）两类。 LSTR 模型形式为：G（γ，c；st） ＝ ｛1 ＋ exp［－γ（st－c）］｝－1，且γ＞0；ESTR模型形式为：G（γ，c；st）＝1－exp［－γ（st－c）2］，且γ＞0 。 特别地，在LSTR模型中，当γ→＋∞时，函数的转移速度会变得无限大，可以实现在阈值处的瞬时变化，此时STR模型就会退化成门限自回归模型（TAR）；当γ→0时，转移函数为确定的值1/2，此时STR模型就会转变为线性模型。

（二）指标变量与数据

STR模型的参数估计所使用的变量指标包括产出缺口、通胀率和通胀预期。本文选取2000年第一季度至2016年第四季度的季度数据，共计65个，数据来源为中经网统计数据库。

1.通胀率。

在经济研究中，用于衡量通货膨胀的宏观经济数据有消费者价格指数（CPI）、商品零售价格指数（RPI）以及GDP平减指数。三者之中，又以CPI与RPI更为普遍，而两者间的区别仅在于消费者价格指数包含了服务价格水平的变动，因而，本文选取消费者价格指数CPI的数据来衡量通胀率。本文中，所选取的CPI数据是官方公布的2000年至2016年的同比数据。由于官方公布的CPI数据仅为月度数据，可通过三个月度的移动平均值作为季度CPI数据，而后通过公式（季度CPI－1）×100%对季度CPI数据进行处理，将其转化为季度CPI通货膨胀率，记为πt。

2.通胀预期。

理论上，通胀预期区分为适应性预期与理性预期。适应性预期是指，经济主体依据过去的信息做出经济决策，即这种预期体现了代理人 “后顾性”的行为特征。而理性预期则假定代理人可以理性地处理影响经济决策的所有信息，并能够依据完全的信息做出符合现实经济运行情况的经济决策，这无疑是对代理人 “前瞻性”行为特征的体现。因此，理性预期相比于适应性预期具有更合理的微观基础，本文所采用的通胀预期即是理性预期。在经济研究中，通常将经济变量的条件期望作为理性预期的代理变量，以理性通胀预期为例，其表达式为Etπt＋1，即代理人能以t期的完全信息对t＋1期的通胀率作无偏一致的估计。在实证研究中，通常将t＋1期的通胀率作为理性通胀预期的测度，本文也采用这一做法。

3.产出缺口。

产出缺口是指实际产出与潜在产出之间的偏差，经济的周期变动常被用来反映总供求之间的差异，并进而影响通货膨胀。因此，对产出缺口的正确估计是建立菲利普斯曲线经济模型的关键。在现有的研究中，估计产出缺口的方法可以分为两类：（1）利用柯布－道格拉斯生产函数估计潜在产出；（2）对实际产出的时间进行分解（线性趋势、HP滤波、卡尔曼滤波）。考虑到HP滤波在趋势剔除方法中的适应性和灵活性，本文采用HP滤波方法来对产出缺口进行估计。首先，为了消除名义GDP中的价格因素，需要以CPI为基础将我国的名义GDP数据转化为实际GDP，其具体做法是：季度实际GDP＝名义 GDP/（1＋CPI）。其次，由于我国的实际GDP数据存在显著的季节因素，为了消除季节因素的影响，本文应用X－12方法对我国的实际季度GDP数据进行了季节调整。最后，利用HP滤波方法将我国的实际季度GDP数据进行分解，得到我国的潜在产出序列，并利用公式：产出缺口＝（实际季度GDP－潜在GDP） /潜在GDP×100，得到我国的产出缺口数据序列，记为yt。

四、实证分析

（一）数据平稳性检验

使用相关变量进行建模之前，应首先对其进行平稳性检验，以确保变量的数据属性能够符合计量模型的要求。本文将采用ADF方法和PP方法分别对变量作平稳性检验。表1给出了检验结果，检验表明在5%的显著水平上，各变量的ADF值和PP值均小于临界值，P值均为0，因而均为平稳序列。

表1 变量的平稳性检验

（二）基于双阈值LSTR模型的我国菲利普斯曲线非线性特征的实证研究

1.我国菲利普斯曲线非线性形式的设定与检验。

由于我国菲利普斯曲线具有混合预期特征，因而本文将我国菲利普斯曲线的形式设定为高阶滞后的混合菲利普斯曲线，并依据式（1）给出其非线性表达式：

其中：πt为当期通胀率；yt为产出缺口；Etπt＋1为通胀预期；πt－i为滞后期通胀率；λ1、λ2为权衡系数；κ1、κ2为预期增广系数；φ1，i、φ2，i为高阶滞后系数；d为滞后阶数；G（γ，c；st） 为一阶或二阶逻辑平滑转移函数（LSTR）。

机制转移函数选择ESTR或LSTR决定了非线性模型以何种方式在不同机制间进行平滑转换。对机制转移函数的选取通常在其三阶泰勒展开式基础上，基于三个贯序检验F统计量的显著性来判断。由于二阶LSTR与ESTR具有相同的泰勒展开形式，区别仅在于其所表示的低机制长度不同，同时考虑到现有研究结论以及我国的现实状况，因而本文将在一阶与二阶逻辑平滑转移函数（LSTR）之间选择G（γ，c，st）的函数形式。

首先，确定非线性混合菲利普斯曲线（2）的滞后阶数d。确定滞后阶数的一般方法是，先通过观察备选序列的相关图得出其可能的滞后阶数，再根据每一滞后阶数下线性自回归方程的AIC值来判断出最优滞后阶数（Granger和 Terasvirta，1993［8］）。 比较通胀序列的相关图，可以将d的范围确定在6阶之内，进一步比较线性AR（d）方程的AIC值，d＝5时AIC值最小，因而选取d＝5作为混合菲利普斯曲线（2）的滞后阶数。

其次，确定LSTR的阈值变量。基于Terasvirta（1994）［24］提出的对STR模型进行非线性检验的可行方法，对转换函数进行三阶泰勒展开，并通过比较不同阈值变量下F统计量的P值来选择合适的阈值变量。本文分别选取1～6阶滞后通胀率、通胀预期和产出缺口作为阈值变量对模型进行非线性检验。表2给出了非线性检验结果，显然，只有在以通胀预期作为阈值变量时，P值最小，菲利普斯曲线非线性特征最显著。

表2 LSTR阈值变量的选取

最后，确定LSTR的函数形式。本文将STR模型的转换函数限定为逻辑平滑转移函数，因而转换函数将在一阶LSTR与二阶LSTR中进行选取。表3给出了通过F统计量计算得到的各贯序假设在5%显著性水平上的P值，结果表明，拒绝原假设H03：β2＝0｜β3＝0的P值最小，这表明在转换函数的泰勒展开式中，二次项的系数不为0，因而应该选择二阶LSTR作为非线性混合菲利普斯曲线（2）的转换函数，结合滞后阶数，我国菲利普斯曲线非线性具体形式可以设定为：

其中：G（·）为二阶 LSTR函数，且G（·）＝｛1 ＋ exp［－γ（Eπt＋1－c1）（Eπt＋1－c2）］｝－1 ；c1和c2为二阶LSTR函数的双阈值。

表3 LSTR转换函数的选取

2.基于双阈值LSTR的我国菲利普斯曲线的非线性特征。

本文采用 Terasvira（1994）［24］提出的网格点搜索方法来估计二阶LSTR函数的转移速度γ和双阈值c1、c2。本文的网格点构造将转移速度限定在0～10的范围内，以其1/30作为步长，同时以转换的变量极差作为搜索区间，仍以其1/30作为步长，共构造900个网格点。同时，为避免转换速度受数据本身大小的影响、无法收敛和过度估计等问题，本文还将二阶LSTR转换函数进行了标准化处理。

当以通胀预期作为转换变量时，通过网格点搜索方法所得到的残差平方和最小且转换速度最大的转换函数为：

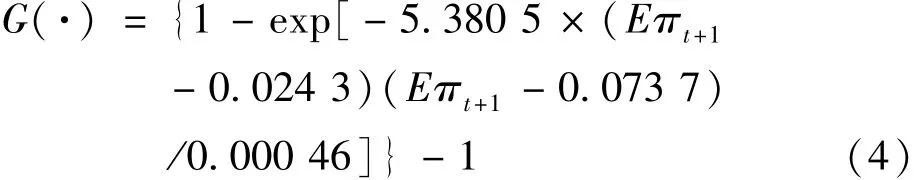
其中，转移速度γ＝5.3805，阈值c1＝0.0243，阈值c2＝0.0737，标准差δs＝0.00046。 式（4） 给出了我国二阶LSTR非线性菲利普斯曲线的转移速度和双阈值。当通胀预期低于2.43%或高于7.37%时，我国菲利普斯曲线处于高机制；当通胀预期位于2.43%～7.37%之间时，我国菲利普斯曲线处于低机制。同时，转换速度为5.3805，说明我国菲利普斯曲线在高低两种机制间的转换是相对迅速的。图1给出了双阈值LSTR的具体转换图。

图1 双阈值LSTR转换函数

将二阶LSTR（4）代入非线性菲利普斯曲线（3），采用NLS方法进行参数估计。表4给出了基于双阈值LSTR的非线性菲利普斯曲线（3）的具体估计值。

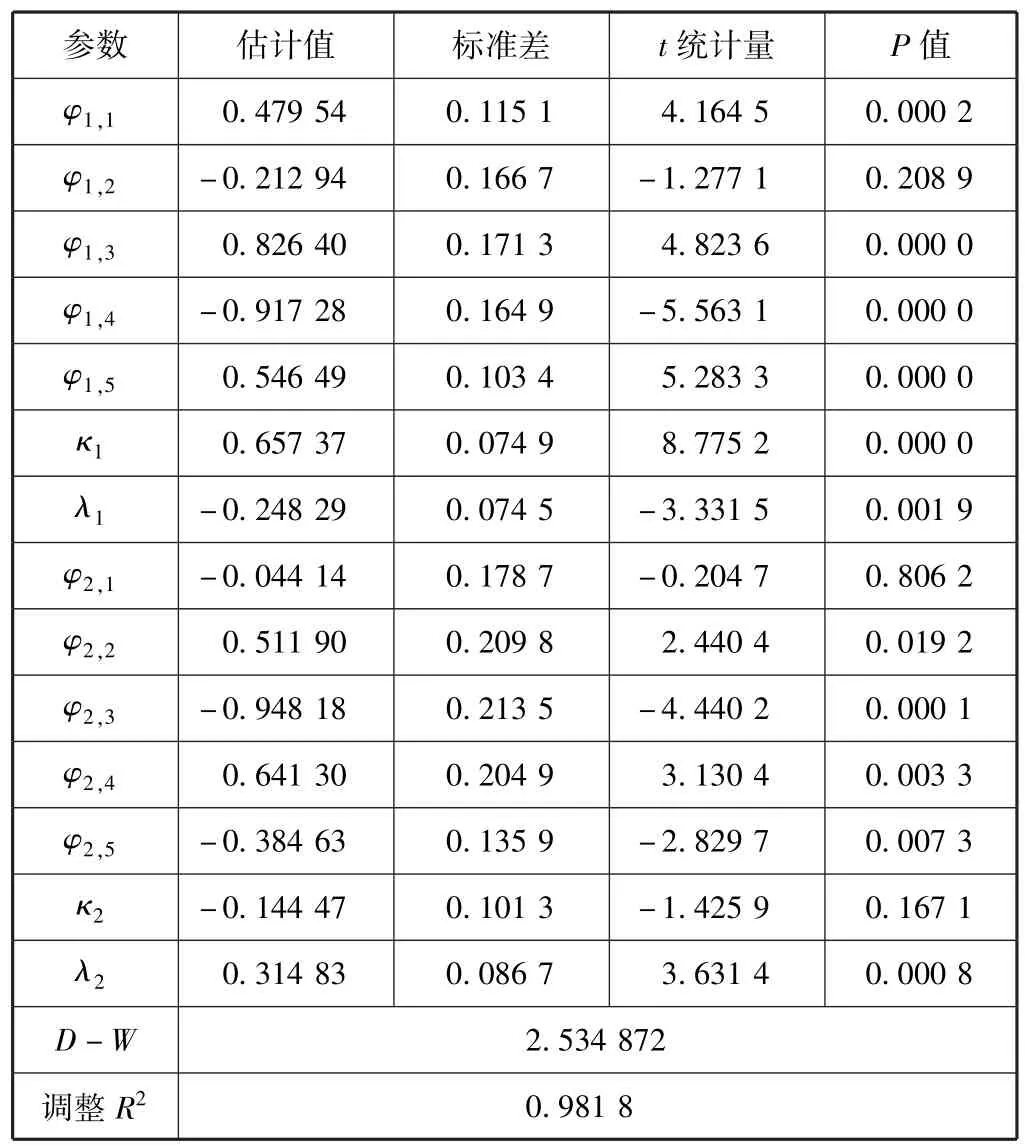
表4 基于双阈值LSTR的非线性菲利普斯曲线的参数估计

为了确保模型的可靠性，本文根据模型本身存在的自相关性与异方差性的强弱来判断模型的整体拟合情况。本文分别使用Ljung⁃Box Q检验和 ARCH⁃LM检验来对模型的自相关性与异方差性进行检验。表5和表6分别给出了双阈值LSTR模型与线性模型的Ljung⁃Box Q检验结果，可以看出尽管非线性模型并未彻底消除模型的自相关性（1、2阶自相关性并不十分显著），但与线性模型相比，其自相关性已经表现得很弱，所以LSTR模型拟合效果较好。表7和表8分别给出了双阈值LSTR模型与线性模型的ARCH⁃LMj检验结果（滞后阶数为3），可以看出尽管线性模型与LSTR模型的条件异方差性质均不显著，但LSTR模型的检验效果仍然要显著好于线性模型。

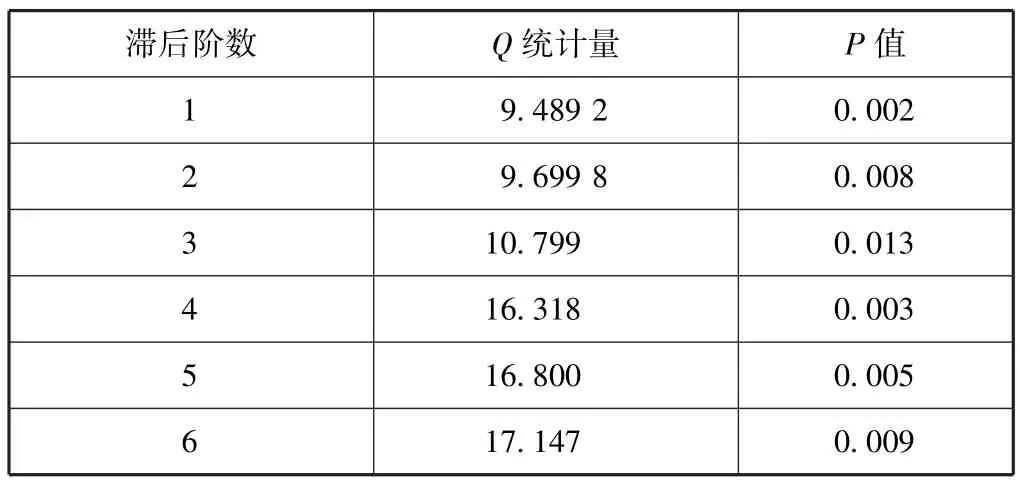
表5 双阈值LSTR模型的自相关性检验

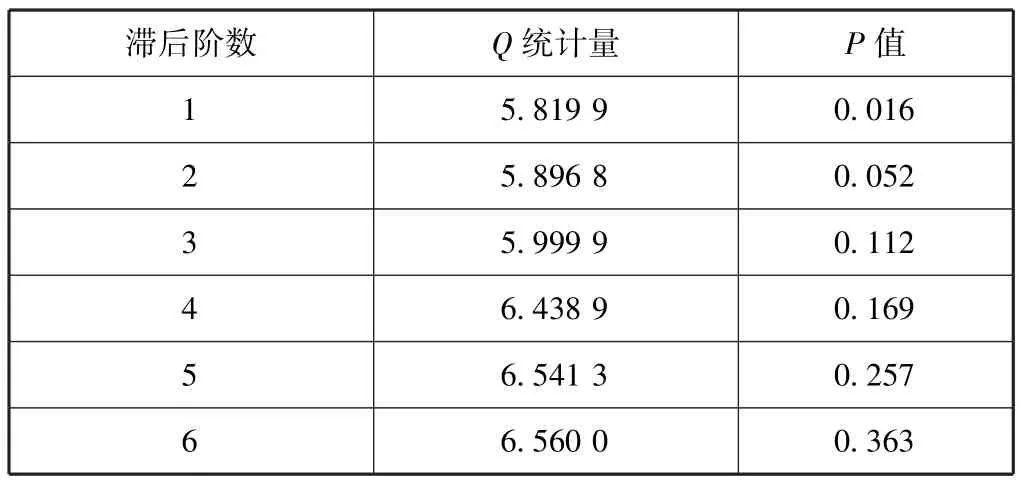
表6 线性模型的自相关性检验

表7 双阈值LSTR模型的ARCH⁃LM检验

表8 线性模型的ARCH⁃LM检验

基于双阈值LSTR的非线性菲利普斯曲线（3）的估计结果（表4）表明，在我国菲利普斯曲线所处的不同机制，其所表示的通货膨胀与其各个影响因素之间的关系也不同。可以将通货膨胀对产出缺口、通胀预期以及滞后通胀的反应系数依次表示为：λ＝λ1＋λ2G（·），κ＝κ1＋κ2G（·），φ＝φ1＋φ2G（·）。

当通胀预期处于中间水平（2.43%，7.37%）时，即我国菲利普斯曲线处于低机制时，转换函数值G（·）趋于0。此时，通货膨胀对于产出缺口的反应系数取决于线性部分λ1，且显著为负（－0.23829），通货膨胀与产出缺口负相关。同时，通货膨胀对于通胀预期的反应系数取决于线性部分κ1，且显著为正（0.65737），通货膨胀与通胀预期正相关。通货膨胀对于各滞后期通胀的反应系数同样取决于线性部分φ1，且只有二期滞后的系数不显著，这表明当我国菲利普斯曲线处于低机制时，通胀惯性显著。

当通胀预期处于较低（低于2.43%）或较高水平（高于7.37%）时，我国菲利普斯曲线处于高机制，转换函数值G（·）趋于1。此时，通货膨胀对于产出缺口的反应系数为λ1＋λ2，且显著为正（0.31482－0.24829＝0.06653），通货膨胀与产出缺口正相关。通货膨胀对于通胀预期的反应系数为κ1＋κ2，而由于其非线性部分的系数不显著，其最终系数仍由其线性部分决定。通货膨胀对于各滞后期的反应系数为φ1＋φ2，尽管其非线性部分的一期滞后系数并不显著，但其他系数均显著，通胀惯性仍然存在。

进一步地，图2给出了我国非线性菲利普斯曲线的区制转移图。从中可以对2000年第一季度到2016年第一季度我国菲利普斯曲线高低机制的分布进行分析。从图中可以看出，我国菲利普斯曲线处于高机制的时段主要分布在2000年至2002年、2004年下半年至2006年年底、2008年下半年至2009年年底，以及2013年下半年至今，其余季度的菲利普斯曲线均处于低机制，且高低机制的转换速度较快。

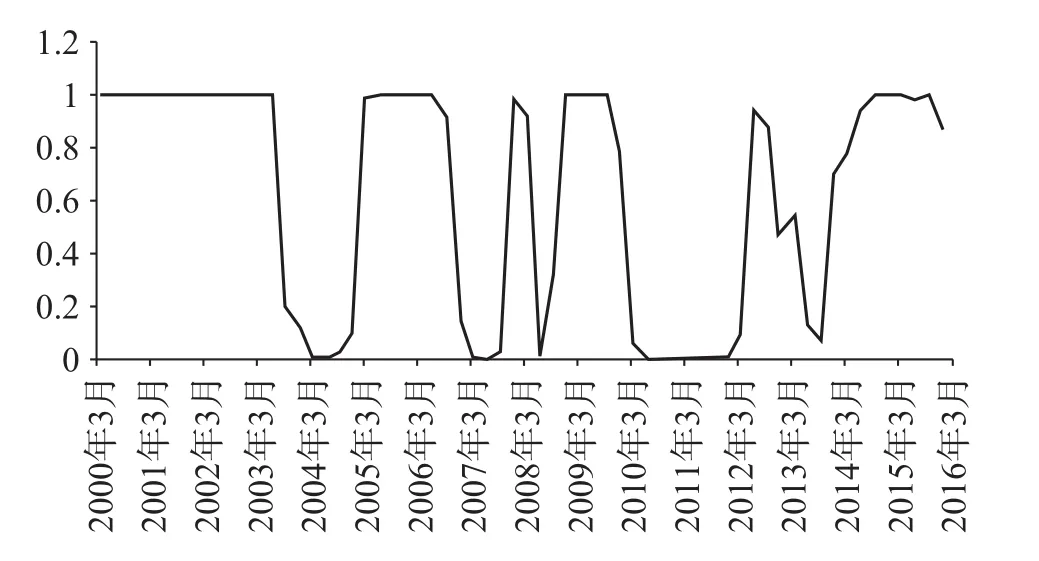
图2 我国非线性菲利普斯曲线的区制转移图

五、结论与建议

采用双阈值逻辑平滑转移机制模型，利用2000年第一季度至2016年第一季度的季度经济数据对我国菲利普曲线的非线性特征进行了实证分析。实证检验结果表明：我国菲利普斯曲线具有通胀预期为阈值变量的二阶LSTR的非线性形式。主要结论和建议如下：

第一，产出缺口对我国通胀具有非对称影响。当通胀预期在（0.0243，0.0737）时，菲利普斯曲线处于低机制，产出缺口系数显著为－0.24829，当通胀预期小于0.0243或大于0.0737时，菲利普斯曲线处于高机制，产出缺口系数为0.06653。当我国通胀预期处于较高或较低水平时，经济增长对通胀的影响更多表现为正向，此时可采取扩张性货币与财政政策来刺激经济增长同时抑制通缩，也可通过紧缩性政策来应对通胀压力。当通胀预期处于中间水平时，经济增长与通胀呈反向变化，此时通过扩张性政策来抑制通缩或通过紧缩性政策来抑制通胀均会适得其反。

第二，通胀预期对我国通胀具有显著正影响。通胀预期是影响我国通胀的关键因素，无论菲利普斯曲线处于低机制或高机制，通胀预期对于通胀影响都取决于菲利普斯曲线的线性部分，其系数为0.65737，且影响程度相对于产出缺口对于通胀的影响更大。因此，通过实施通胀预期管理可以更好地对我国通胀变动进行调控。这需要政府在制定货币政策时应考虑预期因素，通过向公众释放有效信息，使公众产生与政府意图相一致的预期，同时利用公开市场操作的政策微调，强化货币政策调整的信号功能。

第三，我国通胀动态存在惯性特征。在我国菲利普斯曲线的两种机制当中，通胀惯性对我国通胀的影响系数远高于通胀预期与产出缺口的影响系数。当菲利普斯曲线处于低机制时，通胀预期处于中间水平，这种影响更显著且持续性更长。这意味着，政府在制定货币政策时，不仅需要关注短期内各个因素对于通胀的影响，还应考虑通胀动态中存在的惯性特征。通胀惯性特征表明了我国货币政策存在着明显的滞后性，因而实施货币政策时应尽量避免频繁操作，给政策效果的显现留有一定的滞后期。

［1］Phillips A W.The Relation between Unemployment and the Rate of Change of Money Wage Rates in the United Kingdom，1861 －1957 ［J］.Economi⁃ca，1958，25（100）：283－299.

［2］Lipsey R G.The Relation between Unemployment and the Rate of Change of Money Wage Rate： A Further Analysis［J］.Economica，1960，27：1 －17.

［3］Clark P，Laxton D，Rose D.Asymmetry in the US Output⁃inflation Nexus ［J］.Staff Papers International Monetary Fund，1996： 216 －251.

［4］Filardo A J，New Evidence on the Output Cost of Fighting Inflation ［J］.Economic Review，1998（83）： 33 －62.

［5］Dolado J J，Maria⁃Dolores R，Ruge⁃Murcia F.Nonlinear Monetary Policy Rules： Some New Evidence for the U.S.［J］Studies in Nonlinear Dynam⁃ics＆ Econometrics，2004，8（3）.

［6］Engle R F.Estimates of Variances of US Inflation Based on the ARCH Model［J］.Journal of Money，Credit and Banking，1983（15）： 286 －301.

［7］Hamilton J D.A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle ［J］.Econometrica，1989，57（2）：357－84.

［8］Granger C W J，Terasvirta T.Modelling Nonlinear Economic Relationships［M］.Oxford University Press，1993.

［9］Skalin J，Terasvirta T，Another Look at Swedish Business Cycles，1861 －1988 ［J］.Journal of Applied Econometrics，1999（14）： 359 －378.

［10］Bruinshoofd A，Candelon B.Nonlinear Monetary Policy in Europe： Fact or Myth？ ［J］.Economics Letters，2005，86（3）： 399 －403.

［11］陈学彬.对我国经济运行中的菲利普斯曲线关系和通货膨胀预期的实证分析［J］.财经研究，1996（8）：3－8.

［12］刘树成.论中国的菲利普斯曲线［J］.管理世界，1997（6）：21－33.

［13］范从来.菲利普斯曲线与我国现阶段的货币政策目标［J］.管理世界，2000（6）：122－129.

［14］闵正良.对菲利普斯曲线的几点补正［J］.甘肃社会科学，2002（5）：6－9.

［15］张焕明.1979年—2000年我国菲利普斯曲线的实证研究［J］.管理科学，2003，16（2）：78－82.

［16］徐秋慧，李秀玉.菲利普斯曲线研究的最新进展［J］.中央财经大学学报，2008（4）：51－56.

［17］杨继生.通胀预期、流动性过剩与中国通货膨胀的动态性质［J］.经济研究，2009（1）：106－117.

［18］贺根庆，王伟.开放经济条件下中国通货膨胀影响因素的实证研究——基于新凯恩斯菲利普斯曲线［J］.中央财经大学学报，2013（4）：21－26.

［19］刘金全，金春雨，郑挺国.中国菲利普斯曲线的动态性与通货膨胀率预期的轨迹：基于状态空间区制转移模型的研究［J］.世界经济，2006（6）：3－12.

［20］王少平，彭方平.我国通货膨胀与通货紧缩的非线性转换［J］.经济研究，2006（8）：35－44.

［21］陈建宝，乔宁宁.中国菲利普斯曲线的非线性特征分析［J］.统计研究，2013（1）：79－86.

［22］许冰，章上峰.经济转型时期中国的非线性菲利普斯曲线［J］.中国管理科学，2008（5）：37－41.

［23］孙燕.我国产出缺口与通胀菲利普斯曲线形态的研究——基于LSTVAR模型的实证分析［J］.上海经济研究，2012（1）：10－18.

［24］Terasvirta T.Specification，Estimation and Evaluation of Smooth Transition Autoregressive Models ［J］.Journal of American Statistical Association，1994（89）：208－218.