一般阻尼动力系统非奇异摄动法

巨建民 刘新明† 张书娜

(1.大连交通大学土木与安全工程学院, 大连 116028)(2.邢台职业技术学院 建筑工程系,邢台 054035)

一般阻尼动力系统非奇异摄动法

巨建民1刘新明1†张书娜2

(1.大连交通大学土木与安全工程学院, 大连 116028)(2.邢台职业技术学院 建筑工程系,邢台 054035)

借助矩阵摄动理论,将模态叠加法运用于一般阻尼矩阵的动力学方程求解结构的动响应是一种较为理想的方法.但当系统的外荷载激振频率接近于系统的固有频率时,直接将阻尼矩阵作为摄动矩阵,会使解产生奇异,并导致求解失败或误差过大,这是因为模态坐标下的动力学方程是无阻尼方程.为了解决这一问题,本文考虑在模态坐标的动力学方程中保留一定的阻尼.即将阻尼做分解,代入振动方程,得到不同阶次摄动方程,再将摄动方程变换到模态坐标,即采用非奇异摄动方法.最后通过数值算例,得到一阶、二阶摄动,将其与精确解进行比较.精度明显得到改善,基本趋于精确解.从而验证了本方法的精确性和有效性.

动力学, 矩阵摄动, 阻尼矩阵, 非奇异, 模态变换, 摄动量

引言

在工程问题中经常遇到参数小变化的情形,而结构参数小变化引起结构振动特性变化的问题,对工程结构的优化设计有重要意义.矩阵摄动法就是用来研究由于结构参数小变化而引起的结构振动的固有频率和模态向量的变化的方法.文献[1-2]分别介绍了结构振动特征值问题的矩阵摄动法和退化系统振动分析的矩阵摄动法.之后Chen等[3]和Qiu等[4]分别基于一阶矩阵摄动法与一阶参数摄动法提出了计算区间参数结构动力响应的方法.虽然采用一阶区间分析方法可以对区间参数结构动力响应进行分析,但是当参数的不确定量稍大时,采用一阶区间分析方法对结构动力响应范围进行估计可能会失效. Qiu等[5]基于二阶泰勒展开与区间运算,对具有区间参数非线性结构动力响应范围问题进行了讨论. 然而由于此方法涉及到区间运算,得到的结果可能对动力响应范围过分高估,使得这一方法失去实际的工程意义.文献[6]基于二阶摄动展开法与DC算法,提出一种估计区间参数结构动力响应范围的方法,避免了区间运算带来的对结构动力响应的过高估计.

阻尼一直是结构动力学中很难处理的一个问题.例如,模态迭加法是求解结构动态响应较为有效的方法之一,但在考虑结构阻尼时,模态迭加法往往不能直接求解[7],然而,对大部分结构而言,忽略结构阻尼势必造成很大误差[8].过去,在大部分情况下,对于连续体结构,阻尼往往都被忽略掉了,这样的结论对于结构的设计及强度分析也往往不是很有说服力[9-10].考虑到在大部分情况下,阻尼比较小,阻尼对结构动力性能的影响是有限的,因此,动力学方程中的阻尼项可作为数学模型中的摄动项.对于大型结构问题,可使用矩阵摄动方法对此类问题进行求解.对于弱阻尼问题结构频率的求解已有文献论述[11].关于阻尼动力系统的模态分析矩阵摄动法和求解动力响应问题的矩阵摄动模态叠加法,可参考文献[12-13].

借助矩阵摄动理论,将模态叠加法运用于一般阻尼矩阵的动力学方程求解结构的动响应不失为一种较为理想的方法.在大部分情况下直接将阻尼矩阵作为摄动矩阵,都不会出现问题.但是,当系统的外荷载激振频率接近于系统的固有频率时,这种方法会使解产生奇异,并导致求解失败或误差过大.这是因为模态坐标下的动力学方程是无阻尼方程.因此,为了解决这一问题,需要考虑在模态坐标的动力学方程中保留一定的阻尼.即采用非奇异摄动方法.

1 非奇异摄动理论

设一般多自由度系统的振动方程为:

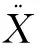
(1)

对于常见的工程问题,阻尼阵[C]的范数小于质量矩阵和刚度矩阵.文献[13]直接将[C]作为摄动矩阵,有时会出现问题.为了在模态坐标的动力学方程中保留阻尼,将阻尼矩阵做如下分解.即:

[C]=[Cd]+[Cr]

(2)

其中,矩阵[Cd]和[Cr]由以下方法确定:

设:[Cdm]=Diag([Φ]T[C][Φ])

(3)

即[Cdm]为阻尼矩阵在使用模态矩阵[Φ]经过模态变换后矩阵主对角元素矩阵.而[Crm]被定义为：

[Crm]=[Φ]T[C][Φ]-[Cdm]

(4)

也就是说[Crm]为[Φ]T[C][Φ]的非对角线元素矩阵.将矩阵[Cdm]和[Crm]变换到物理坐标后为:

[C]=[M][Φ][Cdm][Φ]T[M]+ [M][Φ][Crm][Φ]T[M]

(5)

比较式(2)和(5),即可得矩阵[Cd]和[Cr]的表达式:

[Cd]=[M][Φ][Cdm][Φ]T[M]

(6)

[Cr]=[M][Φ][Crm][Φ]T[M]

(7)

[Cd]可以被称为主阻尼矩阵,[Cr]称为剩余阻尼矩阵.一般来说,剩余阻尼矩阵的范数更小一些,可将其作为摄动矩阵,因此定义:

[Cr]=ε[Cp]

(8)

(9)

依据摄动理论,当参数发生微小变化时,其解也必发生相应变化.设响应[X]的解在摄动后为:

[X]=[X0]+ε[X1]+ε2[X2]+……

(10)

在保留同量级误差的前提下,可得不同阶次的动力学方程:

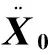
(11)

(12)

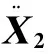
(13)

其余各阶摄动方程依次类推为：

(14)

从求解过程可以看出,其计算过程实为一迭代运算.对于常见的工程问题,一般来说经过几次摄动计算,基本都可以达到一个满意的精度.

2 模态变换解耦和求解过程

模态叠加法是在模态坐标下进行动力学方程的求解.因此,在实际运行中需将摄动方程(11～14)变换到模态坐标.设[q(t)]是方程模态坐标下的响应解.则:

[X(t)]=[Φ][q(t)]

(15)

模态坐标下的各阶摄动的动力学方程可写为:

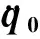
(16)

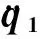
(17)

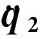
(18)

实际的运行过程可按以下步骤进行：

(1)不考虑阻尼项,对无阻尼动力系统进行模态分析,确定模态矩阵[Φ]和频率矩阵[Λ].

(2)按照式(3)和式(4)确定主阻尼矩阵[Cdm]和剩余阻尼矩阵[Crm],并计算摄动阻尼矩阵[Crmp].

(3)确定模态坐标下的初始条件.

(19)

(20)

(4)由式(16)～(18)计算模态坐标下响应的各阶摄动值[q0],[q1],[q2]等等.

(5)叠加求解总响应值:

[q]=[q0]+ε[q1]+ε2[q2]+…

(21)

(6)将响应值返回到原始坐标:

[X]=[Φ][q]

(22)

3 数值算例

阻尼系统动力学问题的矩阵摄动方法是为较大规模动力学问题设计的.但为了对其计算效果和精度进行分析,这里先以一个简单的二自由度动力方程为例.

某二自由度问题动力方程如下：

其中ω=0.85rad/s

可以看出,阻尼矩阵较质量矩阵和刚度矩阵的范数相对较小.所以,可以把阻尼矩阵作为摄动矩阵,经过模态分析后,可计算出如表1.

表1 非奇异摄动法各阶摄动响应解比较Table 1 Comparison of perturbation response solutions for nonsingular perturbation

从表1可以看出,不考虑阻尼的解与精确解都有一定差距.而通过非奇异摄动法改进后,可以看出,零阶摄动与精确解相比,精度明显得到改善.一、二阶摄动后,基本趋于精确解.

在本例中,由计算得到系统的第一自振频率为0.85,此值与外荷载激振频率0.85相等,但所得到的解并未产生奇异,误差也很小,所以说,一般阻尼动力系统的非奇异摄动法可以很好地解决当外荷载激振频率接近固有频率时,直接将阻尼矩阵作为摄动矩阵所造成的解的奇异性和误差过大问题.

4 结论

(1)大部分工程问题,其材料均为连续介质体(如金属材料、混凝土等),阻尼为结构阻尼,具有弱阻尼特性.运用矩阵摄动理论,提出了依据摄动解计算有阻尼问题动力响应的方法.该方法有效地克服了按常规无阻尼计算时造成的计算误差.

(2)摄动法采用了经典的多自由度动态模态分析理论,简单而实用.与无阻尼问题模态迭加法相比,因为使用了已有的模态和固有频率计算,增加的计算量很小.所以,可以适用大型结构的动力计算.

(3)由算例可以看出,采用非奇异摄动法,即使激振频率等于自振频率,也并未产生奇异,并且精度明显得到提高,二阶摄动后基本趋于精确解.

(4)由非奇异摄动法,将阻尼分解,使模态坐标下的动力学方程转化为有阻尼方程,有效地解决了由于激振频率等于系统固有自振频率时,直接将阻尼阵作为摄动矩阵所造成的解的奇异性以及误差过大问题.

1 陈塑寰. 退化系统振动分析的矩阵摄动法. 吉林工业大学学报, 1981,11(4):11～18 (Chen S H. Matrix perturbation method for vibration analysis of degenerate system.JournalofJilinUniversityofTechnology, 1981,11(4):11～18 (in Chinese))

2 刘应力,陈塑寰. 结构振动特征值问题的二阶矩阵摄动法. 吉林工业大学学报, 1983,29(3):1～11 (Liu Y L, Chen S H. The second order matrix perturbation method for structural vibration eigenvalue problem.JournalofJilinUniversityofTechnology, 1983,29(3):1～11 (in Chinese))

3 Chen S H, Lian H D, Yang X W. Dynamic response analysis for structures with interval parameters.StructuralEngineeringandMechanics, 2002,13(3):299～312.

4 Qiu Z P, Wang X J. Parameter perturbation method for dynamic responses of structures with uncertain-but-bounded parameters based on interval analysis.InternationalJournalofSolidsandStructures, 2005,42(18-19):4958～4970.

5 Qiu Z P, Ni Z. Interval modal superposition method for impulsive response of structures with uncertain-but-bounded external loads.AppliedMathematicalModelling, 2011,35:1538～1550.

6 李琦,邱志平,张旭东. 基于二阶摄动法求解区间参数结构动力响应. 力学学报, 2015,47(1):147～153 (Li Q, Qiu Z P,Zhang X D. Second-order parameter perturbation method for dynamic structures with interval parameters.ChineseJournalofTheoreticalandAppliedMechanics, 2005,47(1):147～153 (in Chinese))

7 陈国平,韦勇. 有阻尼结构现行振动系统的模态综合. 振动工程学报, 2003,16(4):442～445 (Chen G P,Wei Y. Modal synthesis of current vibration system with damping structure.JournalofVibrationEngineering, 2003,16(4):442～445 (in Chinese))

8 蒯行成,李永红,任恒山,等. 一类振动问题中阻尼矩阵的等效方法及应用. 湖南大学学报, 2004,31(1):95～98 (Kuai X C, Li Y H, Ren H S. A damping matrix equivalent method and its application in a kind of vibration problems.JournalofHunanUniversity, 2004,31(1):95～98 (in Chinese))

9 杨育臣. 非比例阻尼结构动力响应分析. 哈尔滨：哈尔滨工业大学, 2009 (Yang Y C. Dynamic response analysis of non-proportional damping structures. Harbin：Harbin Institute of Technology, 2009 (in Chinese))

10刘明辉. 非比例阻尼结构动力学计算方法及在卫星设计中的应用. 哈尔滨：哈尔滨工业大学, 2009 (Liu M H. Computational methods of non-proportionally damped structures with applications to satellite Design. Harbin：Harbin Institute of Technology, 2009 (in Chinese))

11周君求,彭跃社. 求解弱非比例阻尼系统实模态解的阻尼矩阵摄动法. 动力学与控制学报, 2008,6(5):322～326 (Zhou J Q, Peng Y S. Damping matrix perturbation method for solving real mode solutions of weakly non-proportional damping system.JournalofDynamicsandControl, 2008,6(5):322～326 (in Chinese))

12郭永刚,曲乃泗,董毓新. 在非比例阻尼情况下结构动力响应的摄动分析方法. 地震工程与工程振动, 1995,15(4):48～54 (Guo Y G, Qu N S, Dong Y X. A perturbation analysis method for structural dynamic response in the case of non-proportional damping.EarthquakeEngineeringandEngineeringVibration, 1995,15(4):48～54 (in Chinese))

13巨建民,蒙秋男. 具有一般阻尼的结构动力学模态分析的矩阵摄动法. 计算力学研究与进展. 中国力学学会青年工作委员会第三届学术年会论文集.万国学术出版社, 2000:152～156 (Ju J M, Meng Q N. Matrix perturbation method for structural dynamic modal analysis with general damping. Computational Mechanics Research and Development. Proceedings of the 3rd Annual Conference of the Chinese Youth Mechanics Association. Wanguo Academic Publishing House, 2000:152～156 (in Chinese))

† Corresponding author E-mail: liuxinming361@163.com

6 November 2016,revised 30 November 2016.

NON-SINGULAR PERTURBATION METHOD FOR GENERAL DAMPED DYNAMICAL SYSTEM*

Ju Jianmin1Liu Xinming1†Zhang Shuna2

(1.SchoolofCivilEngineeringandSafetyEengineering,DalianJiaotongUniversity,Dalian116028)

Using the matrix perturbation theory, it is an ideal method to apply the modal superposition method to the dynamic equation of general damping matrix to solve dynamic response of structure. However, when the frequency of the system is close to the natural frequency of the system, the damping matrix as the perturbation matrix make the solution singular and lead to the solution failure or large error, because the dynamic equation under modal coordinates is the undamped equation. In order to solve this problem, th consider to retain some damping in the dynamic equation of the modal coordinateshe damping is decomposed and substituted into the vibration equationobtain the different order perturbation equation, and the perturbation equation is transformed to modal coordinatesthe nonsingular perturbation method. Finally, the first-order and second-order perturbation solutions are obtained by numerical examples, which are compared with the exact solutions. The accuracy is improved, basically tend to be the exact solution, which verifies the accuracy and effectiveness of the method.

dynamics, matrix perturbation, damping matrix, non-singularity, modal transformation, perturbation

10.6052/1672-6553-2016-057

2016-11-06收到第1稿,2016-11-30收到修改稿.

† 通讯作者 E-mail: liuxinming361@163.com