基于应变传递率的管道结构损伤识别研究

张 宇，刘锦昆，陈同彦，冯 新

(1.大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116024；2.中石化石油工程设计有限公司， 山东 东营 257026)

基于应变传递率的管道结构损伤识别研究

张 宇1，刘锦昆2，陈同彦2，冯 新1

(1.大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116024；2.中石化石油工程设计有限公司， 山东 东营 257026)

为了研究海底管道损伤识别的分布式监测方法，在标量传递率概念的基础上提出了应变传递率概念和相应的损伤识别方法来对海底管道进行损伤识别，并通过有限元模型模拟对该方法进行了验证。对管道模型的不同损伤程度进行了分析，对比发现该方法相比加速度传递率和理论传递率对损伤程度更加灵敏。对不同边界条件进行分析，发现该方法对损伤位置的识别不受边界条件的影响。对参考单元的选取进行了验证分析，验证了参考单元应选择远离反弯点的非损伤位置。

分布式传感器；标量传递率；应变传递率；损伤识别；损伤指标

自20世纪70年代提出光纤传感技术以来，该技术相比传统传感器以其轻质，抗电磁干扰，耐腐蚀，耐高温，全长分布等优点，逐渐在大跨度结构的健康监测领域获得广泛应用。在海底管道监测时面对管道跨度长，海底工况复杂，容易受到腐蚀和电磁干扰等一系列难题时，应用分布式光纤传感技术能很好的解决问题。分布式光纤传感技术早在损伤检测领域得到研究应用，如Babanajad S K等[1]应用该技术的动态监测能力在15 m长工字钢梁上成功检测出损伤的位置，并指出该方法最小能定位30 μm的微裂缝。Scarella A等[2]提出了一种在斜拉桥模型的桥面上布设分布式光纤传感器，通过应用AT-BOTDA技术测量动态应变的方法成功检测到失效桥索位置并提出基于监测单根桥索对整个桥面的弯矩的应变再分布的损伤定位方法。Wang G A等[3]应用PPP-BOTDA监测管道内壁的腐蚀，将分布式光纤传感器缠绕在管道外表面进行监测，通过与有限元模型结合分析，即可识别管道内壁的腐蚀位置和程度。李兴宇等[4]通过将光纤传感器以0度，120度，240度纵向铺设于埋地管道上，监测了在侵蚀坑作用下的管道变形，提出了对埋地管道完整性的评价方法。张晓威等[5]基于分布式光纤泄漏监测技术进行了泄漏液体与周围介质温度的研究，对管道泄漏的监测具有重要意义。

海底工况复杂，海底管道上沿光纤各位置在不同时段采集到的应变大小都会发生变化，并且海底管道的微小损伤会在涡激振动等的作用下造成管道失效甚至断裂的严重后果。因此，仅从分布式应变数据的时频分析很难发现损伤位置。基于上述原因及现有各种基于结构振动信息的损伤识别方法[6]，传递率函数因其不需对结构进行模态分析，不需要进行数学建模分析，且能最大程度的应用结构各点的应变数据等优点能够有效识别管道结构的损伤。传递率函数是在频域内描述响应自由度之间关系的函数，比较有代表性的工作有：Maia N M M等[7]阐述了传递性函数的基本概念并介绍了其在工程中的广泛应用；Devriendt C等[8]利用传递性函数对模态参数进行了识别，是一种传递率对OMA(Operational/Output-only Modal Analysis)的应用；Weijtjens W等[9]提出瞬时传递率解决荷载的谐响应问题，本质上是对单参考传递率的延伸；Yan W J等[10]提出功率谱密度传递率，引出了传递输出自由度的概念，对传递率的发展做出贡献；Lage Y E等[11]利用传递率矩阵提出一种识别作用于结构力的方法，是对多参考传递率的典型应用；刁延松等[12]利用振动传递率函数和统计假设检验对海洋平台进行结构损伤识别研究。

基于以上提到的成果，本文在标量传递率[13]概念的基础上提出了应变传递率概念和相应的损伤识别方法来对海底管道进行损伤识别，并通过有限元模型模拟，对该方法进行了验证，证明了该方法能有效识别损伤位置、损伤程度和损伤个数。最后本文对该方法应用于实际工程进行了展望。

1 基于传递率的管道结构损伤识别方法

1.1 海底管道结构分析模型与应变传递率

标量传递率(Scalar Transmissibility Function，STF)是描述多自由度系统中的两个不同自由度的响应间的关系，定义为

(1)

式中，w为频域变量；Yi(w)和Yj(w)分别为自由度i和j的运动响应(位移，速度或加速度)的傅立叶变换，分别称自由度i和j为原点自由度和参考自由度；〈Hi(w)〉和〈Hj(w)〉分别是由结构频响函数H(w)中第i行和第j行的元素组成的行向量，{F(w)}为由作用在结构各个自由度上的激励组成的列向量。

由式(1)可知，此时STF的值不仅由结构的频响函数第i行和第j行决定，还由作用于不同自由度的激励{F(w)}决定。其中{F(w)}由不同自由度激励的相对强度，以及激励在频域和空间的分布特征所决定。如果激励完全相关，即激励在频域的分布特征相同，则STF的值只与作用于不同自由度的激励的相对强度和激励的空间分布特征有关，故在波流作用下，海底管道的受力可以近似满足上述条件。

海底管道分析模型可以简化为N个单元组成的梁。考虑海底管道以水平受力为主，而竖向受力很小可以忽略[14]，将作用于管道的波浪力简化为均布作用于各个单元节点上的正弦力。

通过考虑单元应变之间的相互关系，在标量传递率的基础上定义应变传递率，有：

(2)

其中，εi(w)和εj(w)分别为原点单元i和参考单元j的应变傅立叶变换。

根据有限元原理[15]，单元应变与位移响应的关系可以表示为：

ε=[B]{δe}

(3)

其中，[B]为单元的几何矩阵，该矩阵与结构的边界条件以及结构的物理性质有关。{δe}为单元节点位移。将式(1)和式(3)代入式(2)有：

(4)

其中，从式(4)我们可以得到：第一是应变传递率可以写作标量传递率和i、j单元几何矩阵比值的乘积，即应变传递率不仅与标量传递率有关，而且与i、j两个单元的物理性质密切相关，这也决定了应变传递率对局部损伤敏感的性质；第二是应变值可能为正，可能为负，也可能是零，当应变值为零时该单元应变不能作为分母。所以参考单元j不能选取梁的反弯点位置且不宜选在反弯点附近。

至此，将应变传递率应用于损伤识别的使用前提总结为以下5点:

(1) 损伤识别对象应为梁或者可以看作梁的线性结构。

(2) 损伤前后结构的边界条件不能改变。

(3) 损伤前后结构受到的激励在频域的分布特征应该相同。

(4) 损伤前后结构受到的激励沿空间分布和相对大小应该相同。

(5) 应变传递率的参考单元不能选为结构反弯点或者反弯点附近的单元。

1.2 基于应变传递率的损伤指标与识别方法

损伤识别步骤的第一步是构建损伤指标。如果结构发生损伤，则结构在该位置损伤前后的几何矩阵将发生改变，即应变传递率将发生突变。因此应变传递率能够对结构损伤进行精确定位。据此，本文构造了如下损伤指标：

(5)

其中：

(6)

综上所述，将损伤识别步骤分为以下4步：

(1) 选择一个远离结构反弯点的单元x为参考单元，可选结构的跨中单元为参考单元。

2 数值验证

2.1 海底管道数值模型

本节通过管道模型的数值实验对前文提出的基于应变传递率的损伤定位方法进行验证。

本次数值实验采用有限元Pipe16单元建立管道模型。Pipe16是一单轴的具有拉压、扭转和弯曲性能的构件，能很好的对管道的振动进行模拟。模型管道长3.93 m，外径0.2 m，壁厚0.008 m。管道弹性模量为2.63×109Pa，密度为23 337.529 kg/m3，阻尼比为0.002。模型沿长度方向分为了20个相同长度的单元，从左到右依次编号为单元1～单元20。

将作用于管道的波浪力简化为作用于非边界的各个节点上的相同大小的正弦力。通过对结构进行瞬态分析，从而得到结构的各个单元随时间变化的应变数据。其中正弦力公式为f=5 sin(2πt)N。

本次数值模型实验通过对损伤单元的弹性模量E进行折减来模拟损伤的发生。

2.2 基于不同损伤程度对损伤识别方法的比较

对小程度损伤的识别有利于对结构损伤进行提前预警，避免造成更大的事故。在满足1.2节讨论的前提下，对式(1)进行约分得到：

(7)

式(7)直接反映了传递率与结构频响函数的联系，我们将〈Hi(w)〉与〈Hj(w)〉的比值叫做理论传递率。

本次数值实验在简支边界的模型管道上分别利用以理论传递率、加速度传递率和应变传递率三种方法得到的损伤指标D值(参考单元选择单元13)进行了损伤程度为5%、10%、20%的模拟研究(8号单元为损伤单元)，得到图1～图3结果。

从图1～图3我们可以发现，随着损伤程度从5%增大到20%，理论损伤指标D值从1.61增大为2.23，增大1.38倍；加速度损伤指标D值从1.78增大为5.73，增大3.22倍；应变传递率损伤指标D值从22.13增大为116.78，增大5.28倍，因此，应变传递率损伤指标相比另外两种损伤指标对损伤程度更加敏感。

从图形看，应变传递率更容易发现损伤位置，且与前两种图形相比，损伤位置D值相比非损伤位置更加突出。

通过上述讨论可知，应变传递率损伤指标对损伤程度具有很高的灵敏度。

2.3 边界条件对应变标量传递率损伤指标的影响研究

为了探究不同边界条件通过式(4)中几何矩阵对应变传递率损伤指标D值的影响，本节将边界条件简化为两边简支，两边固支和左边简支，右边固支三种，对不同边界条件下7单元进行了损伤程度为20%的损伤模拟，结果如图4～图6所示。

图1 理论损伤指标D值

从图4～图6我们可以发现，无论在何种边界条件下，应变传递率损伤指标都能识别出损伤位置。

与图4两边简支的损伤指标不同的是，在图5和图6两种边界条件下，未损伤位置的D值都有一定程度的增大。

2.4 参考单元选择对应变传递率损伤指标的影响研究

由于结构反弯点位置应变可能为0，由式(6)可知，当εx(w)=0时，应变传递率会出现奇异性，所以参考单元不可以选在反弯点位置。在此节我们将讨论参考单元位置的选择对应变传递率损伤指标的影响。我们通过对两端固支时2单元损伤的模拟，将参考单元x分别选在损伤位置附近的1单元，损伤位置2单元及反弯点位置5单元，由此得到的损伤指标D值图见图7～图9。

图2 加速度损伤指标D值

由图7可知，参考单元选择在损伤位置附近对损伤识别方法没有影响。由图8可知，参考单元选择在损伤位置时，我们无法直接判断出损伤位置，需按照1.2节叙述的损伤位置识别步骤(4)重新选取参考单元。由图9可知，D值数量级变大，也无法对损伤进行识别。综上所述，参考单元应该选择在远离反弯点的非损伤位置处。

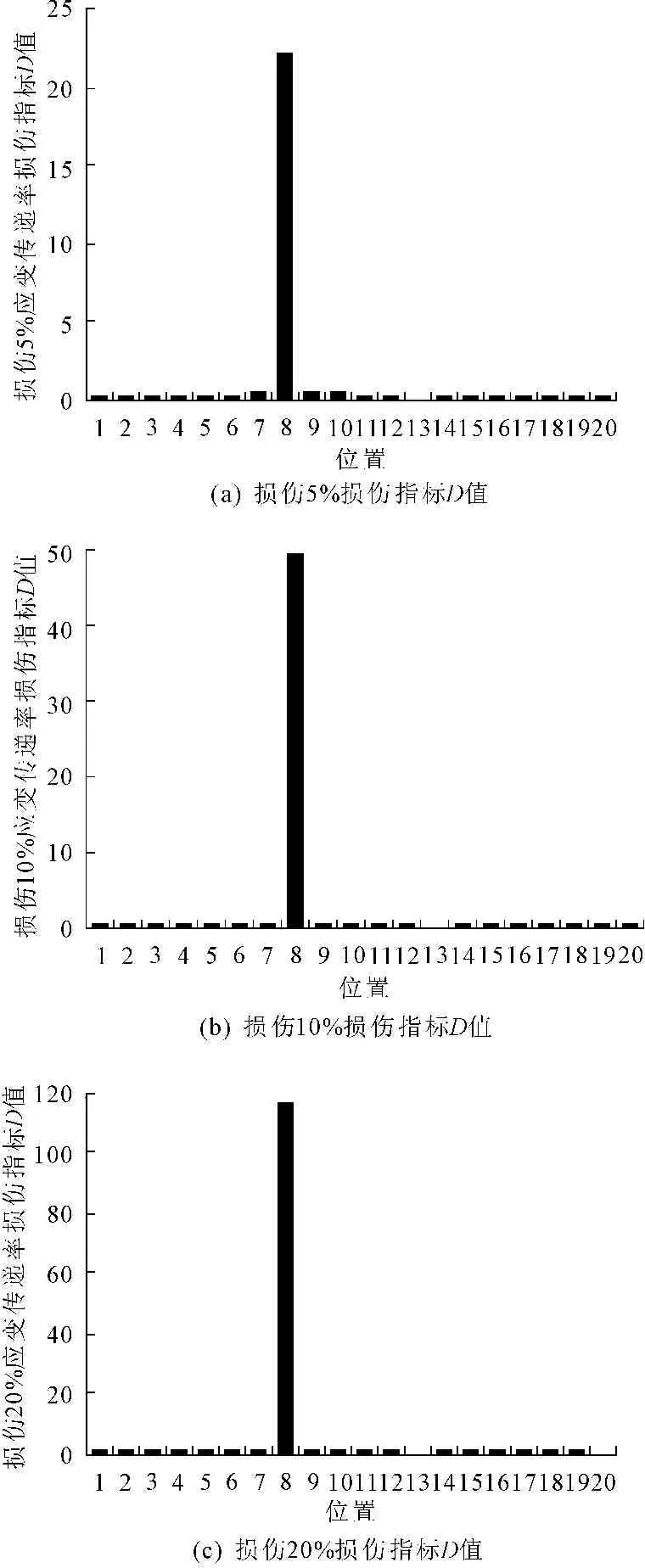
图3 应变标量传递率损伤指标D值

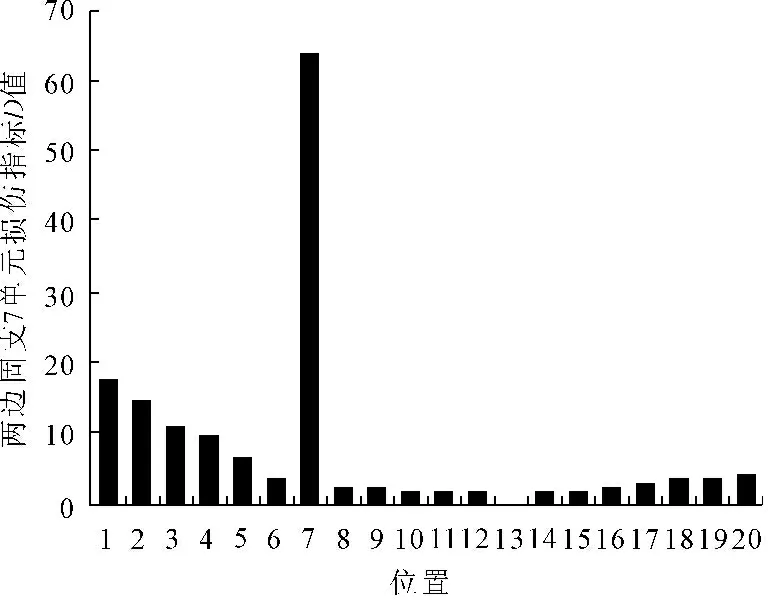
图4 两边简支损伤指标D值图

图5 两边固支损伤指标D值图

图6 左边简支，右边固支损伤指标D值图

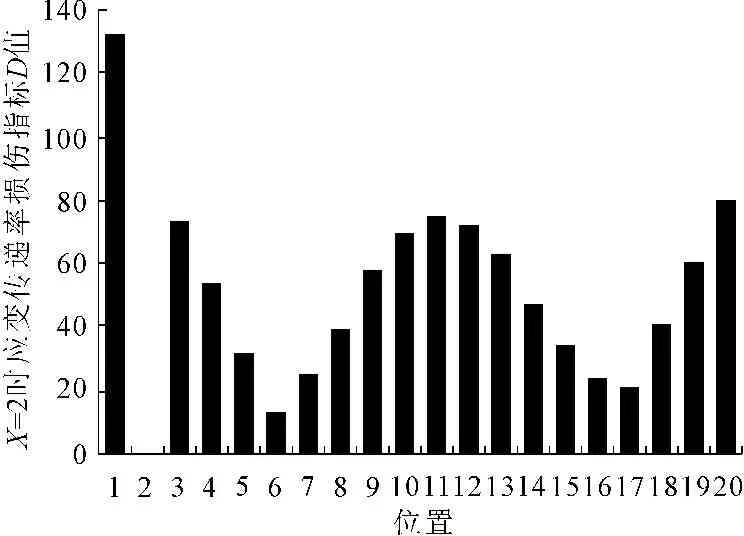
图7 x=1时损伤指标D值

图8 x=2时损伤指标D值

图9x=5时损伤指标D值

3 结 语

本文提出了应变传递率的概念和相应的结构损伤指标和损伤识别步骤。

本文所提出的应变传递率损伤识别方法是对海底管道损伤识别的初步探索，应用于实际工程还有一段距离，相信随着研究的进一步深入，将在海底管道的健康监测领域发挥巨大的作用。

[1] Babanajad S K, Zhan Y, Taylor T, et al. Virtual reference approach for dynamic distributed sensing of damage in large structures[J]. Journal of Aerospace Engineering, 2016:B4016011.

[2] Scarella A, Salamone G, Babanajad S K, et al. Dynamic brillouin scattering-based condition assessment of cables in cable-stayed bridges[J]. Journal of Bridge Engineering, 2016:04016130.

[3] Wang G A, Zhang H. Discrimination of internal wall thinning in pipeline with PPP-BOTDA based distributed optical fiber sensors[J]. Advanced Materials Research. Trans Tech Publications, 2012,424/425:1170-1173.

[4] 李兴宇,卢正刚,吴文婧,等.一种侵蚀坑作用下承插式埋地管道完整性评价方法[J].水利与建筑工程学报,2016,14(3):25-31.

[5] 张晓威,刘锦昆,陈同彦,等.基于分布式光纤传感器的管道泄漏监测试验研究[J].水利与建筑工程学报,2016,14(3):1-6.

[6] 闫桂荣,段忠东,欧进萍.基于结构振动信息的损伤识别研究综述[J].地震工程与工程振动,2007,27(3):95-103.

[7] Maia N M M, Urgueira A P V, Almeida R A B. Whys and Wherefores of Transmissibility[M]. INTECH Open Access Publisher, 2011.

[8] Devriendt C, Guillaume P. Identification of modal parameters from transmissibility measurements[J]. Journal of Sound and Vibration, 2008,314(1/2):343-356.

[9] Weijtjens W, Lataire J, Devriendt C, et al. Dealing with periodical loads and harmonics in operational modal analysis using time-varying transmissibility functions[J]. Mechanical Systems and Signal Processing, 2014,49(1/2):154-164.

[10] Yan W J, Ren W X. Operational modal parameter identification from power spectrum density transmissibility[J]. Computer Aided Civil and Infrastructure Engineering, 2012,27(3):202-217.

[11] Lage Y E, Maia N M M, Neves M M, et al. Force identification using the concept of displacement transmissibility[J]. Journal of Sound and Vibration, 2013,332(7):1674-1686.

[12] 刁延松,徐东锋,徐 菁,等.基于振动传递率函数与统计假设检验的海洋平台结构损伤识别研究[J].振动与冲击,2016,35(2):218-222.

[13] 张 昱,朱 彤,周 晶.多自由度系统中标量传递率的不变性及其应用[J].振动与冲击,2015,34(8):151-156.[14] 王 欣.海底悬跨管道在波浪与地震共同作用下受力分析[D].大庆：东北石油大学,2012.

[15] 李开泰,黄艾香,黄庆怀,等.有限元方法及其应用:发展和应用[M].西安：西安交通大学出版社,1988.

Damage Detection for Pipeline Structures based on Strain Transmissibility

ZHANG Yu1, LIU Jinkun2, CHEN Tongyan2, Feng Xin1

(1.StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian,Liaoning116024,China;2.SinopecPetroleumEngineeringCorporation,Dongying,Shandong257026,China)

In order to study the distributive monitoring methods of damage detection in submarine pipelines, this article proposed the concept of strain transmissibility and relevant methods of damage detection to recognize the damage in submarine pipelines bases on the concept of scalar transmissibility and Moreover, the methods were verified by finite element model. Variant damage degrees are analyzed with pipeline models. Through comparison, it is found that the methods are more sensitive than acceleration transmissibility and theory transmissibility, and damage indexes are linear to damage degrees. Analysis of boundary conditions finds that by using those methods the detection of damage sites is not affected by boundary conditions. The choice of reference modulus is analyzed and validated that reference modulus should be chosen from the undamaged positions away from the inflexion point. The methods can detect damage in submarine pipelines, and thus lay the foundation of applying distributive sensors to monitoring the health of submarine pipelines.

distributed sensor; scalar transmissibility; strain transmissibility; damage detection; damage index

10.3969/j.issn.1672-1144.2017.03.011

2017-02-01

2017-03-03

国家自然科学基金面上项目(51378088)；国家重点研发计划项目(2016YFC0802402)

张 宇(1992—)，男，山西孝义人，硕士研究生，研究方向为水工结构健康监测。E-mail: zhangyuqh@foxmail.com

冯 新(1971—)，男，河北昌黎人，教授，主要从事结构健康监测方面的工作。E-mail: fengxin@dlut.edu.cn

P756.2

A

1672—1144(2017)03—0054—06