岩土参数随机场计算机模拟及其工程应用

张继周，王华敬，刘福胜，徐玉

(1.中设设计集团股份有限公司，江苏 南京 210014；2.山东农业大学 水利土木学院， 山东 泰安 271018；3.北京师范大学 地理学与遥感科学学院， 北京 100875)

岩土参数随机场计算机模拟及其工程应用

(1.中设设计集团股份有限公司，江苏 南京 210014；2.山东农业大学 水利土木学院， 山东 泰安 271018；3.北京师范大学 地理学与遥感科学学院， 北京 100875)

基于随机场模拟的局部平均细分法理论，借助随机数发生器的子程序库，实现随机场可靠性分析的计算机模拟，并结合有限元软件ANSYS的后处理模块将模拟结果可视化，进而分析离散尺寸和相关距离对模拟结果的影响，通过工程实例，应用随机场计算机模拟结合Monte-Carlo抽样分析的手段，进行工程可靠性分析。结果表明随着相关距离的增加，随机场的变化特性减慢；越靠近上部的土层，土性参数的不确定性对基础沉降的概率反映特性的影响越大。研究成果不仅提供岩土参数随机场计算机模拟的实现方法，而且诠释其应用过程，完善随机场理论在岩土工程可应用领域的一个重要拼图。

随机场理论；计算机模拟；可靠性分析；Monte-Carlo抽样；有限元方法

岩土参数随机场模型是用有限样本点的观测数据描述整个土层剖面的空间变异性特征，而随机场的计算机模拟是将抽象的随机场模型还原到土体的天然状态，前者体现由具体到一般的抽象过程，后者诠释由一般到具体的应用过程。就目前来看，虽然研究者们在岩土参数随机场的描述方面进行了广泛研究[1-3]，但在数值分析领域针对岩土工程问题的各种商业计算软件无一例外采用的是确定性分析方法，无法考虑计算过程中的不确定性。学者们认识到随机方法的重要性[4-5]，但如何在数值计算领域考虑土性参数的不确定性，关键是如何将土性参数空间点与点之间的变异性传递到实际的计算过程当中去。随机场的计算机模拟实质是土层剖面的再现过程，可以解决上述问题。

有关随机场计算机模拟的算法，目前最为通用的主要有六种[6-8]：移动平均法、离散傅里叶变换法、快速傅里叶变换法、协方差矩阵分解法、转动条带发、局部平均细分法。各种算法的理论基础、实现步骤，以及在模拟过程中的精度、效率和使用便捷性，可参考文献[9]。本文基于随机场模拟的局部平均细分法理论，借助随机数发生器的子程序库，实现随机场的计算机模拟，并结合有限元计算软件ANSYS的后处理模块将模拟结果可视化，进而分析离散尺寸和相关距离对模拟结果的影响；最后，通过工程实例，应用随机场计算机模拟结合Monte-Carlo抽样分析的手段，进行工程可靠性分析。

1 随机场模拟的局部平均细分法

局部平均细分法最早由Fenton G A[7]于1990年在其博士论文中首次引入，其目的主要是配合随机场的局部平均理论而提出的一种模拟方法。不同于其它算法的是，它的理论基础并非来源于随机信号处理技术，而是着眼于工程应用，优点是极易与现有数值计算领域所广泛采用的有限元方法相结合，因为待模拟区域经过局部平均细分后，每个单元的模拟值可以作为有限元所离散出单元的随机输入值，从而应用Monte-Carlo抽样的方法即可方便地进行相应工程问题的随机分析，其理论推导及实现过程参考文献[9]，本文的重点是模拟结果的分析和工程应用。

图1 局部平均细分法示意图

2 随机场的模拟结果分析

为了直观形象地展示随机场的模拟结果，笔者借助有限元计算软件ANSYS的后处理模块，将局部平均细分法的随机场计算机模拟值进行了可视化处理。图2分别为一维、二维、三维情况下随机场的局部平均细分法模拟结果示意图，各自代表随机场在一次抽样条件下的样本函数。

图2 随机场模拟结果示意图

值得说明的是，要完全展示一个三维情况下的随机场模拟结果，至少需要一个四维空间，即x、y和z方向上的坐标值以及在特定坐标点的随机场模拟值。然而四维空间无法用图形直观显示，只能靠抽象思维去想象。所以三维情况下给出的实际是空间内竖直方向上z=a处的平面在三维情况下的模拟结果，可以想象，当z取遍区间[0，10]内的所有数值之后，对于任意一个z值，都将有一个类似模拟结果图与之对应，叠加后即是实际三维空间下的随机场模拟结果。需要注意的是，虽然以上分析看似一种叠加，但三维随机场的模拟结果却是一次形成的，并非针对每一个z值进行一次二维随机场的模拟，再将它们组合成三维的，以上分析只是在四维空间无法用图形直观展示的条件下的无奈之举。

2.1 离散尺寸对模拟结果的影响

为了分析离散尺寸对模拟结果的影响，并考虑表达问题的方便性，本节选用二维随机场的模拟结果进行分析，因为二维情况下的随机场模拟结果比较容易展示，并且直观形象，可以用x、y方向上的坐标值再加上颜色坐标从而在二维空间内直观地体现三维元素。图3分别为平面内的正方形区域通过选取不同离散尺寸进行离散的随机场模拟结果，其中不同单元内的不同颜色代表该单元内随机场模拟值的大小。

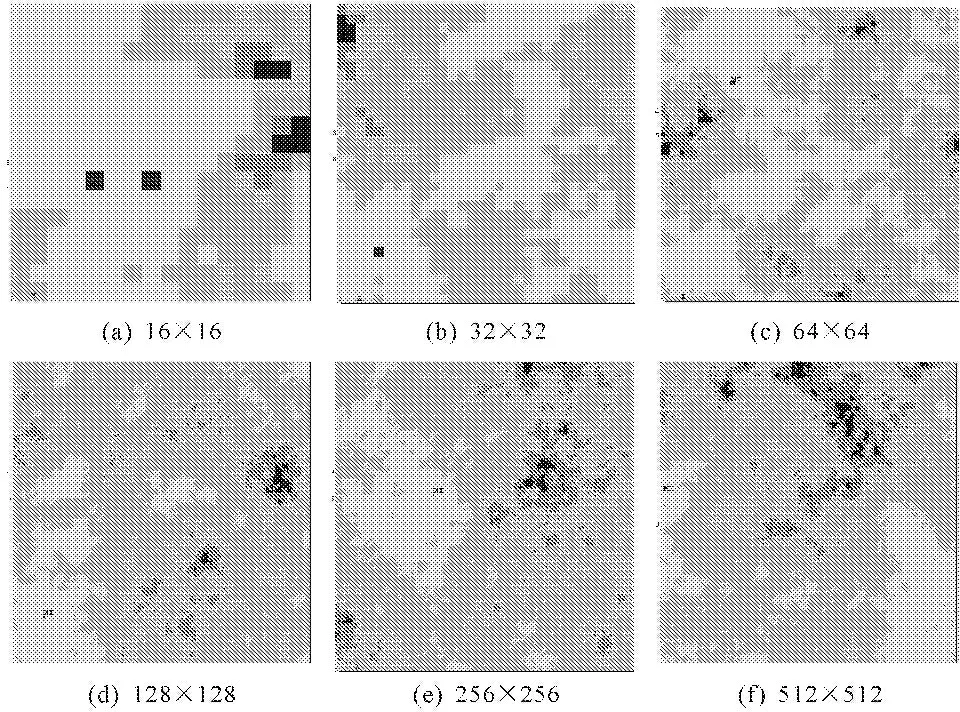
图3 不同离散尺寸的模拟结果

图3中平面区域分别被离散为16×16、32×32、64×64、128×128、256×256、512×512个单元，直观上看，随着离散尺寸的减小，图形由粗糙逐渐变得平滑，代表性也越来越好。事实也是如此，因为随机场的模拟实质是用离散单元上的彼此相关的随机变量来近似表达连续随机场，网格越疏，离散出的随机变量就越少，代表性越差；网格越密，离散出的随机变量就越多，代表性越好。但是随着网格的逐渐加密，计算量将急剧增加，以及在后续计算中与有限元结合的难度也将越来越大。因此，实际应用时，根据具体工程的需要，考虑精度、效率和使用方便性的平衡十分必要[10-11]。

需要说明的是：以上展示的以及接下来将要展示的随机场模拟结果图，本质上都是随机场在一次抽样条件下的样本函数，正因如此，加之随机场本身的特性，所以在不同的抽样过程中，不可能得到两个完全一模一样的随机场表示，如若如此，就无所谓随机了。

2.2 相关距离对模拟结果的影响

根据随机场的基本理论，相关距离是表示随机场变化快慢的量，体现着场内点与点之间的自相关特性，当相关距离较小时，随机场变化较快，反之随机场变化较慢，图4形象地示意了这一点。图中分别为随机场在不同相关距离条件下(θx、θy分别表示水平和竖直向相关距离)的模拟结果，可以看出，随着相关距离的增加，场内相邻单元离散值的相关性在增强，随机场的变化特性在减慢，体现在图形上即是场内相邻单元的颜色越发接近，颜色间的变化也越来越缓和，场内邻近单元相同颜色的区域在逐渐增大。

当取水平向和竖直向相关距离不等时更能说明情况，当水平向相关距离取20.0而竖直向相关距离取0.2时，可以看出水平向上的颜色变化明显要慢于竖直向上的颜色变化，说明在水平方向上相邻单元的离散值的相关性要比竖直方向上相邻单元的离散值的相关性强，反之亦然。特别地，在极值情况下，即当相关距离趋于无穷大时，意味着场内任意两点都完全相关，此时可将其模拟为随机变量，体现在样本函数上即每次抽样的样本函数为一常数。

图4 不同相关距离的模拟结果

3 随机场模拟的工程应用

随机场计算机模拟的工程应用，最直接也是最常见的是将其与较为盛行的有限元方法相结合，从而实现对构筑物在特定荷载条件下的工程反映特性的Monte-Carlo抽样分析，习惯上称为随机有限元法，或者更准确地称为Monte-Carlo法随机有限元。我们对于确定性有限元方法已经十分熟悉，那么对于随机有限元的概念又当如何呢？

Monte-Carlo法随机有限元的实质是对构筑物中不确定性指标进行随机Monte-Carlo抽样，然后针对抽样结果进行确定性有限元分析，最后再把多次抽样计算的结果进行统计分析，从而得到构筑物的概率反映特性。例如在基础沉降分析方面，如果将所要用到的土性参数看作是不确定性的(或者说是随机的)，并将其建模为随机场，同时取得了相关随机场的各种指标参数，便可以利用上面介绍的随机场的计算机模拟方法进行多次模拟，并将每次模拟样本应用到确定性有限元分析中，最后，通过对多次计算结果进行统计分析即可得到基础沉降的概率反映特性。

3.1 计算模型

假设某刚性条形基础长L=5.0 m，基础荷载F=1 000 kN，作用在深度H=10.0 m的软土地基上，地基土为单层且下卧基岩。为了对基础沉降进行概率分析，进而用于可靠度设计，选择如图5所示的计算尺寸和有限元剖分模式，即计算深度取为整个土层，计算宽度取为地基深度的3倍；计算区域被剖分为60×20的有限元计算网格，水平方向上离散为60个单元，竖直方向上离散为20个单元。

图5 模型尺寸及有限元网格

考虑土性参数的不确定性，此处将地基土的弹性模量E建模为服从对数正态分布的随机场，泊松比μ的不确定性暂不考虑，取为确定值0.3，如此建模的依据可参考文献[12-13]，且根据文献[14-15]统计结果，假设弹性模量随机场E(x,y)的相关指标已经统计得到，取均值μE=30 MPa、标准差σE=9 MPa、相关距离θE=0.9 m(为分析问题方便，此处假设地基土为各向同性，即水平向和竖直向相关距离相等)，自相关函数形式为：

(1)

利用随机场的计算机模拟方法，结合图5的有限元剖分模式，即可对基础沉降进行Monte-Carlo抽样分析，进而统计各次抽样的计算结果，得到基础沉降的概率反映特性。此处随机场的离散单元与有限元网格重合。

3.2 计算结果的统计分析

针对上述计算模型，笔者对基础的沉降进行了5000次的Monte-Carlo模拟计算，图6示意了其中一次模拟计算的基础变形情况，图6中在有限元网格上叠加了随机场的模拟结果，不同单元上体现为弹性模量E的自然对数。

图6 基础变形示意图

由于基础假设为刚性，所以其下表面沉降处处相等，从图6中也可以直观地看出。因此，对沉降结果进行统计分析时，只需考虑地基表面、基础中心处的沉降即可。为此，每次Monte-Carlo抽样分析后，记录地基表面、基础中心处单元节点的沉降计算结果，通过5000次Monte-Carlo模拟计算，共得到5000个这样的沉降值，其统计特性如表1所示，相应的分布情况如图7所示。

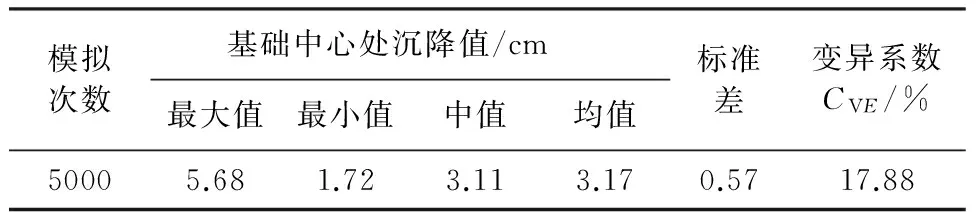
表1 模拟结果统计分析

由以上结果，不仅可以掌握基础沉降的大小范围和分布情况，还可以利用文献[15]介绍的方法方便地对基础沉降进行概率预报和可靠性分析。

3.3 地基土分层对沉降统计结果的影响

以上是假设地基土为单层情况下的基础沉降的Monte-Carlo随机有限元分析，然而实际工程中面对地基土往往是成层分布的，那么，当地基土为多层情况时，随机场的模拟又当如何进行？不同的分层情况对基础沉降统计计算结果又有何影响呢？为此，笔者在原有程序的基础上又进行二次开发，考虑地基土分层后土性参数在层与层之间的不连续性，将其假设为相互独立，从而实现了成层地基土的随机场的分层模拟。图8为两层地基土在层间土性参数具有不同变异系数条件下的随机场模拟结果，其中上层土弹性模量的变异系数CVE1，下层土弹性模量的变异系数CVE2；图9为两层地基土在层间土性参数具有不同相关距离条件下的随机场模拟结果，其中上层土弹性模量的相关距离θE1=0.2 m，下层土弹性模量的相关距离θE2=2.0 m。

图7 基础沉降柱状图

图8 层间土不同变异系数的随机场模拟结果

图9 层间土不同相关距离的随机场模拟结果

为了分析不同分层情况对基础沉降统计计算结果的影响，笔者利用3.1部分的计算模型，假设不同的地基土分层状况，分别进行了多次Monte-Carlo抽样分析，并将结果汇总于图10～图12中。其中图10表示假设地基土弹性模量随机场的均值、变异性和自相关性指标都固定，仅仅人为对地基土分层情况下，不同的分层数对基础沉降变异性统计结果的影响；图11表示假设地基土分为两层情况下，在上下两层地基土的弹性模量随机场的变异性取不同值时，分层位置对基础沉降变异性统计结果的影响，其中H1/H2表示上下两层土的厚度之比；图12表示假设地基土分为两层情况下，在上下两层地基土的弹性模量随机场的相关距离取不同值时，分层位置对基础沉降变异性统计结果的影响。

图10 分层数对统计结果的影响

图11 不同变异性下分层位置对结果的影响

图12 不同相关距离下分层位置对结果的影响

从图10可以看出，当土层剖面随机场的均值、变异性和自相关性指标不变时，人为增大地基土的分层数会导致统计所得的基础沉降的变异性降低，这主要是因为增大分层数实质是增大土层剖面内土性参数之间的不相关性，也即减小土性参数的相关距离，由文献[3,16]可知，相关距离越小，土工构筑物在空间平均效应下的方差折减系数将越小，方差折减的越多，从而反映到基础沉降上即沉降的变异系数越小。

从图11和图12中可以看出，上层土的变异性和自相关性指标对基础沉降计算结果的统计特性影响较为显著，可以说上层土性参数的随机场模型指标几乎控制着基础沉降的概率反映特性，这主要是因为地基土在基础荷载作用下，附加应力场的强度会随着深度的增加而不断减弱，越靠近上部的土层其附加应力越大，对应的计算沉降在总沉降中所占的比重越大，因而，越靠近上部土层的不确定性对整个基础沉降的概率反映特性的影响也将越大。所以，当分析实际问题时，应根据不同土层的权重程度不同，有针对性的选取模型参数，这样才能做到心中有数、有的放矢。

4 结 论

岩土参数随机场的计算机模拟是在数值分析领域将随机场理论应用于岩土工程可靠性分析的必经环节。本文就随机场模拟的计算机实现过程、模拟结果分析、工程应用开展研究，主要得到以下几点有益的结论：

(1) 随机场的计算机模拟实质是土层剖面的再现过程，它不仅可以在数值计算中体现土性参数空间点与点之间的变异性，而且能够实现对整个土层剖面进行土性参数预测的目的，开展此方面的研究是一项基础性的重要工作。

(2) 离散尺寸对模拟结果的影响表现为：随着离散尺寸的减小，图形由粗糙逐渐变得平滑，其代表性也越来越好，但计算量也在增加，以及在后续计算中与有限元结合的难度也越来越大，因此实际应用时应综合考虑。

(3) 相关距离大小反映随机场变化的快慢，随着相关距离的增加，场内相邻单元的离散值的相关性增强，随机场的变化特性减慢，体现在图形上即是场内相邻单元的颜色越发接近，颜色间的变化也越来越缓和，场内邻近单元相同颜色的区域在逐渐增大，极值情况下，即相关距离趋于无穷大时，意味着场内任意两点都完全相关，即每次抽样的样本函数为一常数，实质为一随机变量。

(4) 通过对工程实例的Monte-Carlo随机有限元分析发现：人为对地基土进行分层会导致沉降计算结果的统计变异性降低，分层数越多，降低越显著；越靠近上部的土层，其土性参数的不确定性对整个基础沉降的概率反映特性的影响越大；另外，工程实例还展示了随机场的计算机模拟在土工可靠性分析中的应用过程。

[1] 郭林坪，杨爱武，闫澍旺，等．天津港地区土层剖面随机场特征参数的估计[J].工程地质学报，2016,24(1):130-135.

[2] 张继周，缪林昌，林 飞，等．苏中腹地湖相沉积土层相关距离的统计分析[J]．工程地质学报，2014,22(2):348-454.

[3] 闫澍旺，朱红霞，刘 润，等．关于土层相关距离计算方法的研究[J]．岩土力学，2007,28(8):1581-1586.

[4] 董晓红,梁桂兰,许忠厚.边坡稳定分析方法综述及发展趋势研究[J].水利与建筑工程学报,2012,10(5):100-102，106.

[5] 王忠涛,周思超.随机荷载作用下饱和松砂的动力特性试验研究[J].水利与建筑工程学报,2015,13(5):55-59.

[6] Fenton G A. Error evaluation of three random-field generators[J]. Journal of Engineering Mechanics, 1994,120(12):2478-2497.

[7] Fenton G A. Simulation and analysis of random fields[D]. New Jersey: Princeton University, 1990.

[8] Fenton G A, Griffiths D V. Risk assessment in geotechnical engineering[M]. New York: John Wiley & Sons, 2008.

[9] 张继周．区域性软土土性参数随机场模型与随机固结沉降的研究与应用[D]．南京：东南大学，2010.[10] 傅旭东，茜平一，刘祖德．浅基础沉降可靠性的Neumann随机有限元分析[J]．岩土力学，2001,22(3):285-290.[11] Liu P L, Liu K G. Selection of random field mesh in finite element reliability analysis[J]. Journal of Engineering Mechanics, 1993,119(4):667-680.

[12] 张继周，缪林昌，陈俊波．苏中腹地湖相软土土性参数变异性统计描述[J]．岩土力学，2010,31(2):471-477.

[13] 张继周，缪林昌．岩土参数概率分布类型及其选择标准[J]．岩石力学与工程学报，2009,28(S2):3526-3532.

[14] Zhang J Z, Miao L C, Wang A T. Characterization of variability of marine soft soil properties[C]//Proceedings of the International Symposium on Lowland Technology. Korea:Busan, 2008:117-123.

[15] 张继周，缪林昌．基于随机场理论的地基概率沉降分析[J]．岩土工程学报，2010,32(7):1059-1064.

[16] Vanmarcke E H. Random Fields: Analysis and Synthesis[M]. London: Cambridge MaMit Press, 1983.

Computer Simulation and Engineering Application of Soil-parameter Random Field in Geotechnical Engineering

ZHANG Jizhou1, WANG Huajing2, LIU Fusheng2, XU Yushen3

(1.JiangsuProvincialCommunicationsPlanningandDesignInstituteCo.,Ltd.,Nanjing,Jiangsu210014,China;2.CollegeofWaterConversancyandCivilEngineering,ShandongAgriculturalUniversity,Tai’an,Shandong271018,China3.SchoolofGeography,BeijingNormalUniversity,Beijing100875,China)

Based on the local average subdivision algorithm and the subroutine library of random number generators, computer simulation of random field were obtained and visualized by adopting the post processor of ANSYS. Hence, two common influential factors such as discrete sizes and correlation distances were analyzed. In addition, a case study was conducted to verify the effectiveness of the computer simulation using Monte-Carlo sampling method. The results show that with the increase of correlation distance, the features of change of random field slow down. As near to upper soil layer, the uncertainty of soil parameters greatly impacts the probability characteristics of foundation settlement. The conclusions of this paper can not only provid approaches to simulate the representative random fields of soil profiles, but also demonstrate procedures in engineering application. Furthermore, it can be very helpful to develop the technology systems about applications of random field theory for reliability analysis in geotechnical engineering.

random field theory; computer simulation; reliability analysis; Monte-Carlo sampling; FEM

10.3969/j.issn.1672-1144.2017.03.002

2016-12-14

2017-02-04

国家科技支撑计划资助项目(2015BAB07B05)

张继周(1983—)，男，河南驻马店人，博士，高级工程师，主要从事岩土工程设计、咨询和概率设计方法及工程应用方面的工作。 E-mail:55109992@qq.com

王华敬(1971—)，女，山东招远人，博士，副教授，主要从事岩土工程方面的教学科研工作。E-mail:hj.wsd@163.com

TB115

A

1672—1144(2017)03—0008—06