POVMD与包络阶次谱的变工况滚动轴承故障诊断

姜战伟， 郑近德， 潘海洋， 潘紫微

(安徽工业大学机械工程学院 马鞍山，243032)



POVMD与包络阶次谱的变工况滚动轴承故障诊断

姜战伟， 郑近德， 潘海洋， 潘紫微

(安徽工业大学机械工程学院 马鞍山，243032)

针对变转速滚动轴承故障特征提取较难的问题，提出一种基于参数优化变分模态分解(parameter optimized variational mode decomposition，简称POVMD)与包络阶次谱的变工况滚动轴承故障诊断方法。首先，采用POVMD对变转速滚动轴承振动信号进行分解，得到若干个本征模态函数之和；其次，对各个分量的时域信号进行角域重采样，将时变信号转化为平稳信号处理，再利用Hilbert变换估计重采样后的平稳信号的包络；最后，对得到的包络信号进行阶比分析，从谱图中读取故障特征信息。将POVMD方法与经验模态分解进行了对比，仿真信号分析结果表明了POVMD方法的优越性。将提出的变转速滚动轴承故障诊断方法应用于试验数据分析，分析结果表明，所提出的方法能够实现变转速滚动轴承的故障诊断，而且诊断效果优于现有方法。

变分模态分解; 变工况; 包络阶次谱； 滚动轴承； 故障诊断

引 言

滚动轴承是传动系统中最容易损坏的元件之一[1]。当滚动轴承发生故障时，振动信号大多数是多分量调幅调频信号[2-3]，轴承故障引起的振动特征表现为振动信号中存在冲击脉冲，从而使振动具有明显的非平稳特征。传统的以恒定转速和平稳信号为前提的故障诊断方法不再适合处理这类信号。滚动轴承升降速过程的振动信号比平稳过程的信号复杂得多，往往包含了丰富的状态信息。变速过程的振动信号更能反映微弱故障特征，一些在平稳运行中不易反映的故障特征在升降速过程中可能充分地表露出来[4]。因而，对滚动轴承变工况条件下振动信号进行分析显得尤为重要。

阶比分析技术[5-9]将时域非平稳信号转化为角域平稳信号进行分析，是分析旋转机械变工况非平稳振动信号十分有效的方法。但是，由于振动信号的复杂性及噪声干扰，直接对原始信号进行阶比分析，往往诊断效果不够明显，且干扰成分较多。对振动信号的各个模态进行分离，再对特定的模态进行阶比分析，不仅能够有效地抑制噪声干扰，而且也能够达到更好的诊断效果。

故障诊断领域常用模态分离的方法主要有小波变换[10]和经验模态分解(empirical mode decomposition, 简称EMD)等。但是小波变换本质上是基于积分理论，因此对非平稳信号分析存在局限性和困难性[11]，而且分解依赖于小波基的选择，不具有自适应性。EMD是非平稳信号分析方法[12-13]，能自适应地将一个复杂信号分解为若干个本征模态函数(intrinsic mode function, 简称IMF)和一个趋势项之和。但EMD存在包络误差、模态混淆和端点效应，缺乏严格的数学理论支持，其中的递归筛选存在不允许反向误差校正和不能够恰当地处理噪声等缺陷[14]。Dragomiretskiy等[15]在传统维纳滤波的基础上，提出了一种非递归的自适应信号分解方法——变分模态分解(variational mode decomposition，简称VMD)。VMD方法将信号分解问题转化为约束优化问题，以最小带宽为约束条件得到瞬时频率具有物理意义的调幅调频信号，自适应地将一个复杂信号分解为若干个IMF之和。VMD具有精度高和收敛速度快的特点，消除了指数衰减直流偏移，非常适合处理滚动轴承故障振动信号[16]。Wang等[17]利用VMD检测转子系统的碰摩故障，得出了VMD性能优于经验小波变换[18]、EMD和总体平均经验模态分解[19]的结论。但是VMD方法中模态个数K需要事先给定，其他参数的选择缺乏理论依据。针对VMD方法的不足，文献[20]利用粒子群优化算法对VMD的参数进行优化，提出了参数优化变分模态分解，并将其应用于轴承早期故障的检测。文献[20]采用Shannon熵评价信号稀疏特性，以熵值的大小来反映概率分布的均匀性。然而对于早期轴承微弱故障，由于随机事件的发生表现出不确定性，用概率表示故障随机可能性大小的度量并不十分合理。模糊熵是一种衡量时间序列复杂性的有效方法[21-22]。考虑到模糊熵采用模糊隶属函数来表示元素的属于程度，所以用模糊熵来衡量轴承微弱故障信号的复杂度更加合适。基于此，笔者提出了基于包络模糊熵的参数优化变分模态分解(parameter optimized variational mode decomposition, 简称POVMD)与包络阶比分析的滚动轴承故障诊断方法，并将其应用于实验数据分析。结果表明，所提出的方法能够有效地提取变转速下滚动轴承的故障特征。

1 参数优化变分模态分解

1.1 变分模态分解

VMD是一种自适应信号分解新方法，其利用迭代的方法求解变分模型的最优解，从而获取各个IMF的频率中心和带宽，能够自适应地将各IMF分量有效分离。为了估计每一个模态的带宽，受约束的变分问题如下

s.t.Σkuk=f

(1)

其中：{uk}={u1,u1,…,uK}和{wk}={w1,w2,…,wK}分别代表一系列模态函数及其中心频率。

为了使上述约束问题变为非约束变分问题，引入二次惩罚因子α和拉格朗日乘法算子λ。增广拉格朗日乘子表达式如下

(2)

为了更新uk,利用实值信号埃尔米特对称，给出非负频率区间上的半空间积分形式

(3)

(4)

中心频率ωk不在重构保真度项中，而仅仅出现在带宽项中，即

(5)

同理，将其变换到频域

(6)

解得中心频率的更新方法，更新的ωk为相应模态函数功率谱的重心

(7)

VMD算法具体过程如下：

2)n=n+1,执行整个循环；

3)k=k+1，直到k=K，更新uk

(8)

4) 更新

(9)

5) 更新λ

(10)

1.2 参数优化变分模态分解

从算法过程看，VMD非递归地将多分量信号分解成一系列有限带宽的本征模态函数之和，非常适合处理多分量调幅调频信号。但是，VMD方法处理信号时需要预先设定模态个数和惩罚参数。对此，笔者考虑利用粒子群优化算法对变分模态分解算法的最佳影响参数组合进行搜索，自动筛选出最佳的影响参数组合，再根据所得结果设定变分模态分解算法的惩罚参数和分量个数，从而可避免人为主观因素的干预。

1) 初始化粒子群算法中的参数，即PSO参数局部搜索能力c1，PSO参数全局搜索能力c2、最大迭代次数N、速率与位置的关系系数k、速率更新公式中速度前面的弹性系数wV以及种群更新公式中速度前面的弹性系数wP；

2) 以局部极小模糊熵值最小化作为粒子群优化算法的适应度函数；

3) 初始化粒子群算法的种群，将VMD算法的参数组合[α,K]作为个体位置，随机产生与种群数量相当的影响参数组合作为种群中个体的初始化位置，随机初始化每个粒子个体的移动速度；

5) 对比适应度值大小并更新个体局部极值和种群全局极值；

6) 更新粒子的速度和位置；

7) 循环迭代，转至步骤4，直至迭代次数达到最大设定值后输出最佳适应度值及粒子的位置。

2 基于POVMD与包络阶次谱的变工况滚动轴承故障诊断方法

2.1 理论方法

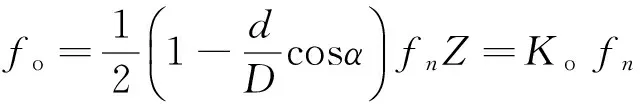
(11)

(12)

其中：fn为转速；Z为滚动体个数；d为滚动体直径；D为轴承节径；α为接触角；Ko，Ki分别为滚动轴承外圈故障、内圈故障特征阶次系数。

笔者提出一种基于POVMD与包络阶比分析的变工况滚动轴承故障诊断方法，具体步骤如下：

2) 确定阶比分析的最大分析阶次Nmax，依据采样定理，采样率至少应为最大分析阶次的2倍；

3) 选取包含丰富故障信息的最佳分量(按分量中心频率从高到底选取)，对其进行角域重采样，得到重采样信号vi(θ)；

(13)

(14)

2.2 仿真信号分析

为了验证POVMD方法的分解效果，首先考虑式(15)所示的仿真信号x(t)=x1(t)+x2(t)+x3(t)

(15)

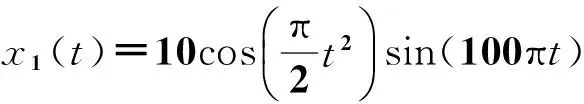
x(t)由3个调幅-调频信号叠加而成，它们的时域波形如图1所示。

为了说明POVMD方法的优越性，首先采用EMD和VMD方法对信号进行分解，结果如图2和图3所示。图2中，经EMD分解得到3个IMF分量和一个残量，而且分解结果出现了频率混淆。图3中，原VMD(设定参数[α=280,k=3])分解结果中，只得到了2个分量，而且它们严重失真，这是由于人为设定VMD参数的原因，并没有考虑参数影响。

图1 仿真信号及其3个分量波形Fig.1 Simulation signal and its three components

图2 仿真信号的EMD分解结果Fig.2 EMD decomposition results of simulation signal

图3 仿真信号的VMD分解结果Fig.3 VMD decomposition results of simulation signals

图4 仿真信号的POVMD分解结果Fig.4 POVMD decomposition results of simulation signal

采用POVMD方法对上述信号进行分解，最佳参数优化组合为[α=694,k=7]，分解结果如图4所示。从图中可以看出，POVMD能够有效地将3个分量分离，由POVMD分解得到的结果与原始信号中的3个分量一致，具有很好的保真度。因此，上述对比分析结果表明，POVMD能够有效地分离混合信号的各个模态，且效果优于VMD和EMD方法。

2.3 试验验证

为了验证本方法的有效性，在滚动轴承试验台上进行正常状态、滚动轴承外圈故障和内圈故障3种工况的瞬态试验。本研究采用6037型的深沟球轴承进行试验，通过激光切割在外圈和内圈上开槽来设置故障，槽宽为0.15 mm，槽深为0.13 mm。将加速度传感器安装在轴承座上，采样频率为8 192 Hz。对于6037E型滚动轴承，d=13.5 mm，D=57.5 mm，α=00，Z=8，由此计算出滚动轴承外圈故障、内圈故障的故障特征阶次系数Ko，Ki分别为3.060 9和4.939 1。

不失一般性，对7.08～9.52 s升速过程的转速信号进行分析，如图5(a)所示。图5(b)为其对应的振动加速度信号时域波形。随着转速的提高，幅值也相应地变化，能量逐渐加强，这说明振动加速度信号与转速有直接关系。采用POVMD方法对外圈故障振动加速度信号进行分解，寻优得到的最佳参数组合[k,α]=[5,489]，分解结果如图6(a)所示。由图可知，分解得到了5个分量，分别为u1(t)，u2(t)，u3(t)，u4(t)和u5(t)。由于滚动轴承故障信息往往位于振动信号的相对高频段，而低频一般为转速和干扰噪声，因此，笔者选择前3个中心频率相对高的分量进行角域重采样，每一转采样128个点，得到的重采样角域如图6(b)所示。最后，对重采样后的角域信号进行包络阶比分析，得到如图7所示的包络阶次谱。从分量的阶次谱中很明显地看出有多处谱峰值3.017，6.129，9.17和12.21等，分别对应着滚动轴承1倍、2倍、3倍和4倍外圈故障特征阶次。这说明滚动轴承外圈有故障，与实际情况一致。

采用POVMD方法对减速过程的具有内圈故障的滚动轴承振动信号进行分析。转速信号如图8(a)所示。图8(b)为对应的加速度信号时域波形。采用POVMD方法对信号进行分解，寻优得到最佳参数组合[k,α]=[5,180]。分解得到了5个分量，分别为u1(t)，u2(t)，u3(t)，u4(t)和u5(t)，结果如图9(a)所示。 选取前3个相对高频的分量进行角域重采样，每一转采样128个点，得到图9(b)所示的角域分量v1(θ)，v2(θ)和v3(θ)。再对重采样后的角域信号进行包络阶比分析，得到如图10(a)和(b)所示的包络阶次谱。从角域分量v2(θ)和v3(θ)的阶次谱中都可以很明显地看出，谱峰值0.913 7，2.027和2.917分别近似地对应滚动轴承参考轴1倍、2倍和3倍特征阶次；谱峰值4.944，9.937和14.88等分别对应滚动轴承内圈1倍、2倍和3倍等故障特征阶次。从角域分量v3(θ)的阶次谱中可以看出，谱峰值0.889 9，2.027和2.917等分别对应着滚动轴承参考轴1倍、2倍和3倍特征阶次；谱峰值4.944，9.937和14.88等分别对应滚动轴承内圈1倍、2倍和3倍等故障特征阶次。这说明滚动轴承内圈有故障，与实际情况一致。

采用上述方法对正常滚动轴承的振动信号进行分析，图11(a)和(b)分别为4.96～6.71 s升速过程正常滚动轴承的转速信号及振动加速度信号，采样频率为8 192 Hz。采用POVMD方法对其分解， 最佳参数组合[k,α]=[7,4 165]。选取前3个中心频率相对高的分量进行角域重采样，其中每转采样点数为128， 重采样后的信号如图12(a)所示， 对应分量的包络阶次谱如图12(b)所示。从谱图中找不到滚动轴承故障特征阶次，与实际情况符合。

图5 具有外圈故障的滚动轴承转速信号和振动加速度信号Fig.5 Rotating speed and vibration signals of rolling bearing with outer ring fault

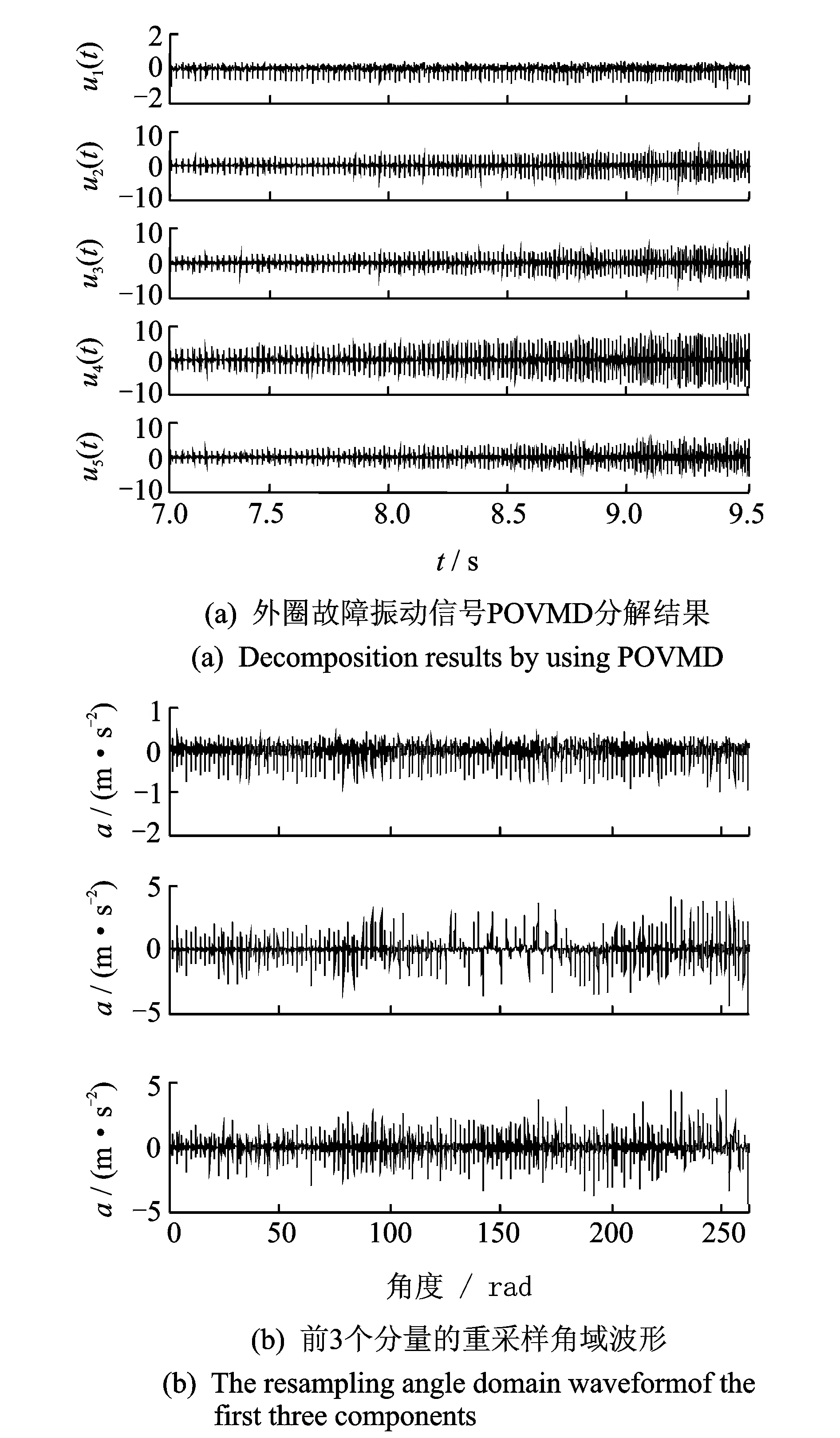
图6 具有外圈故障轴承振动信号的POVMD分解结果及前3个分量的重采样角域信号Fig. 6 The POVMD decomposed results of vibration signal of bearing with the outer ring fault and theresampling angular domain signal of the first three IMFs

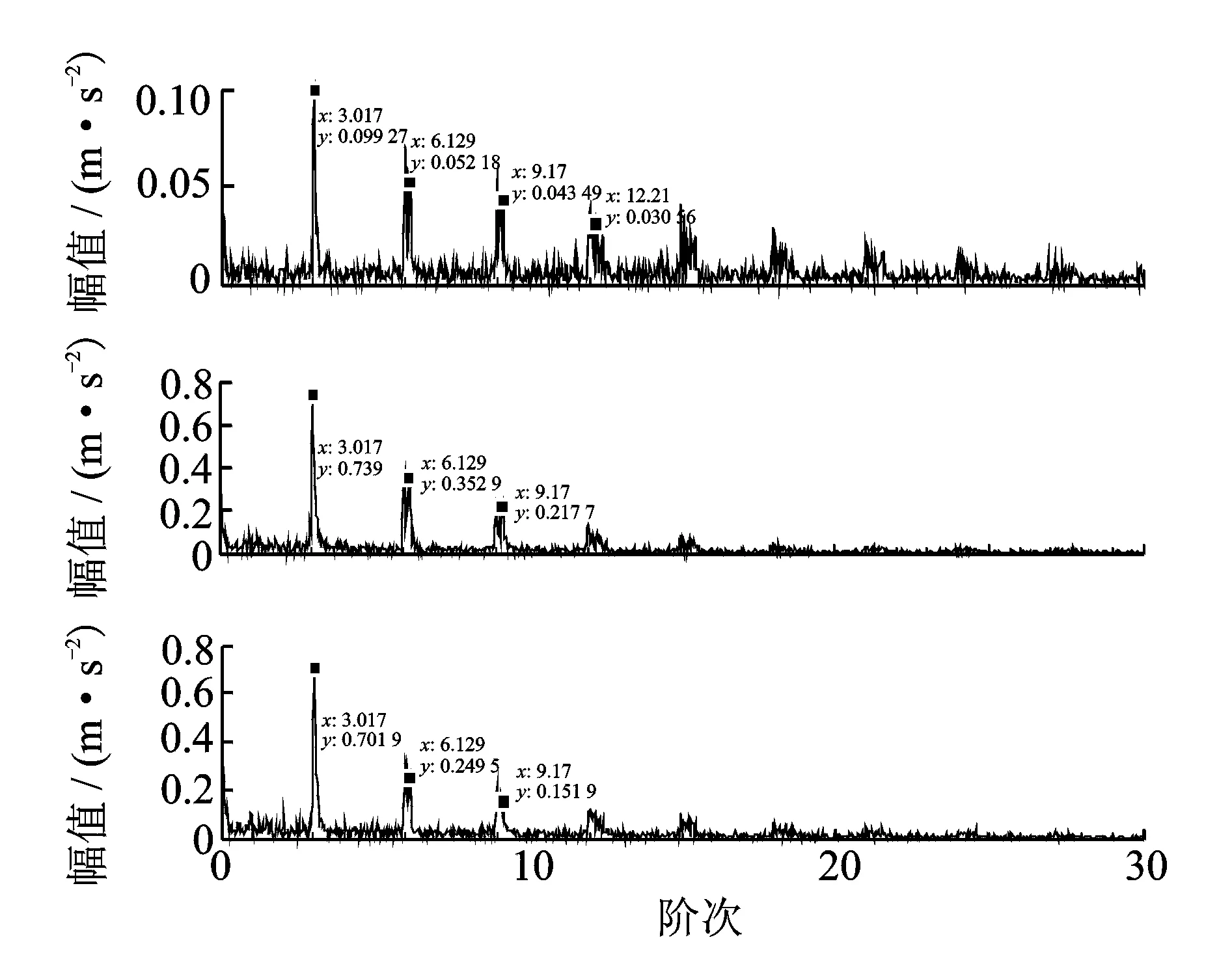
图7 具有外圈故障振动信号的包络阶次谱Fig.7 Envelope order spectrum of the vibration signal with outer ring fault

图8 具有内圈故障的滚动轴承转速信号和振动加速度信号Fig.8 Rotating speed and vibration acceleration signals of rolling bearing with inner fault

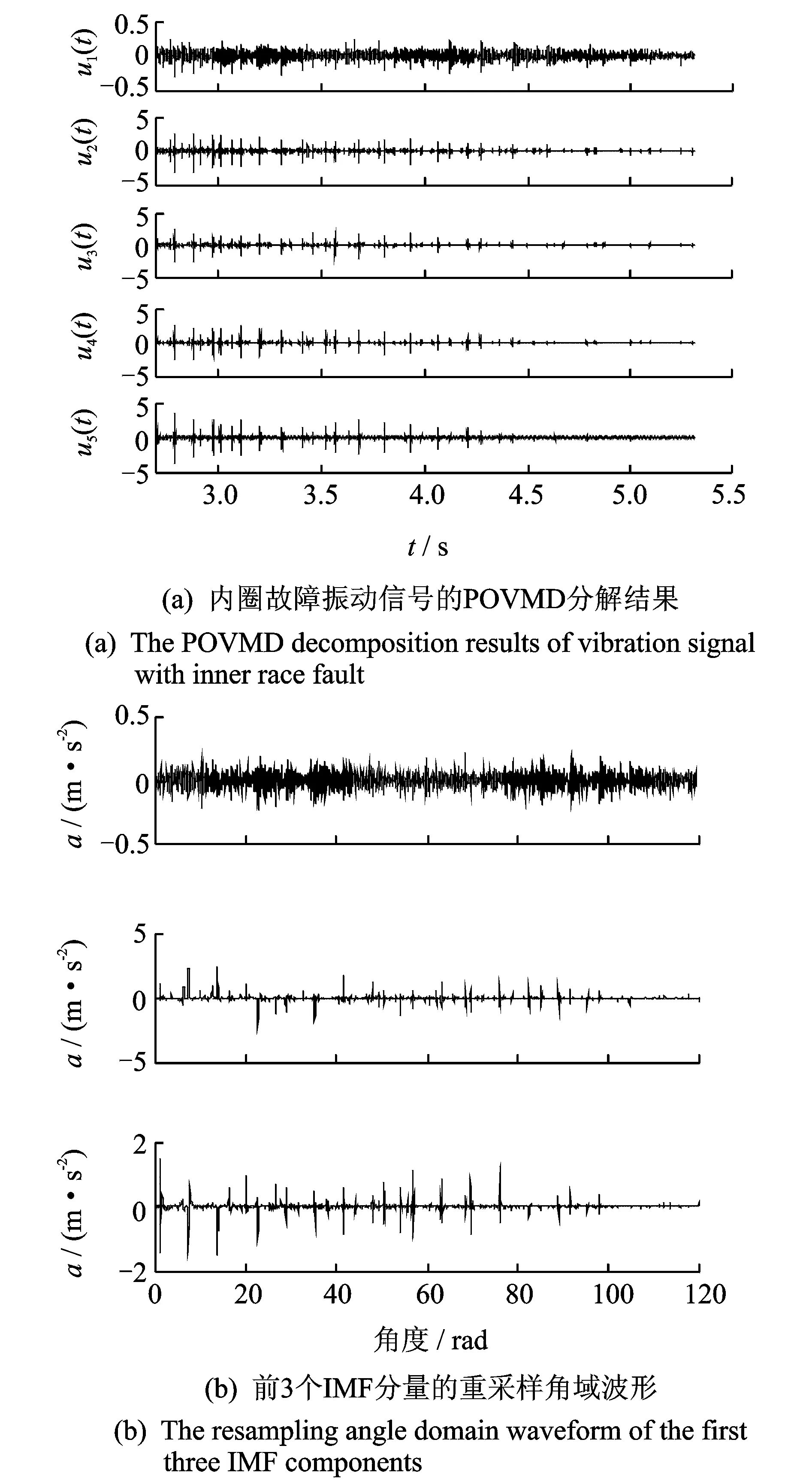
图9 内圈故障轴承振动信号的POVMD分解结果及前3个分量的重采样角域信号Fig.9 The decomposed results of the vibration signal of bearing with inner race fault and the resampling signal inangular domain of the first three IMF components

图10 具有内圈故障振动信号分解分量v2(θ)和v3(θ)的包络阶次谱Fig.10 Envelope order spectrum of v2(θ) and v3(θ) with inner ring fault

图11 正常滚动轴承的转速信号和振动加速度信号Fig.11 Rotational speed and vibration acceleration signals of the normal rolling bearing

图12 正常滚动轴承振动信号POVMD分解分量重采样后的角域波形及其包络阶次谱Fig.12 The resampling IMFs of POVMD result of vibration signal of normal bearing and theirenvelope order spectrum

上述分析和对比结果表明，笔者提出的方法能够有效地诊断变转速条件下滚动轴承的故障诊断。

3 结 论

1) 提出了一种参数优化的变分模态分解方法POVMD。通过仿真信号分析，将其与EMD和VMD进行对比。结果表明，POVMD方法能够避免EMD的频率混叠现象，其分解效果优于EMD和VMD方法。

2) 提出一种基于POVMD与包络阶次谱的变工况滚动轴承故障诊断方法，并将它应用于滚动轴承实验数据分析。结果表明，所提出的变工况滚动轴承故障诊断方法能够准确地提取出滚动轴承故障特征信息。

[1] 田福庆，罗荣贾，兰俊.机械故障非平稳特征提取方法及其应用[M].北京：国防工业出版社,2014:66-88.

[2] Feng Zhipeng, Chen Xiaowang, Liang Ming, et al. Time-frequency demodulation analysis based on iterative generalized demodulation for fault diagnosis of planetary gearbox under nonstationary conditions[J]. Mechanical Systems & Signal Processing, 2015,62:54-74.

[3] 丁康，孔正国，何志达.振动调幅信号的循环平稳解调原理与应用[J].振动工程学报，2005，18(3)：304-308.

Ding Kang，Kong Zhengguo，He Zhida. The principle and application of cyclostationary analysis for demodulation of amplitude modulated signals [J].Journal of Vibration Engineering, 2005，18(3)：304-308. (in Chinese)

[4] 马辉,王雪玲,牛和强,等.升降速过程中转子系统油膜失稳规律[J].振动、测试与诊断,2016(1):56-61.

Ma Hui, Wang Xueling, Niu Heqiang, et al. Oil film instability of rotor system during the process of lifting speed[J].Journal of Vibration, Measurement & Diagnosis, 2016(1):56-61. (in Chinese)

[5] Fyfe K R, Munck R D S. Analysis of computed order tracking[J]. Mechanical Systems and Signal Processing, 1997,11(2):187-205.

[6] Bossley K M, Mckendrick R J. Hybrid computed order tracking[J]. Mechanical System and Signal Processing, 1999,13(4)：627-641.

[7] Guo Y, Tan K K. Order-crossing removal in Gabor order tracking by independent component analysis[J]. Journal of Sound and Vibration, 2009,325(1):471-488.

[8] Guo Y, Tan K K. High efficient crossing-order decoupling in Vold-Kalman filtering order tracking based on independent component analysis[J]. Mechanical Systems and Signal Processing, 2010,24(6):1756-1766.

[9] 张亢,程军圣.基于LMD和阶次跟踪分析的滚动轴承故障诊断[J].振动、测试与诊断,2016,36(3):586-591.

Zhang Kang, Cheng Junsheng. Roller bearing fault diagnosis based on LMD and order tracking analysis[J].Journal of Vibration, Measurement & Diagnosis, 2016,36(3):586-591. (in Chinese)

[10]赵玲,刘小峰,娄路.复小波分解联合SVD提取振动信号非平稳特征[J].振动、测试与诊断,2015,35(4):672-676.

Zhao Ling, Liu Xiaofeng, Lou Lu. The feature extraction method of non-stationary vibration signal based on SVD-complex analytical wavelet demodulation[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(4):672-676. (in Chinese)

[11]胥永刚, 孟志鹏, 陆明.双树复小波包和ICA用于滚动轴承复合故障诊断[J].振动、测试与诊断,2015,35(3):513-518.

Xu Yonggang, Meng Zhipeng, Lu Ming. Compound fault diagnosis of rolling bearing based on dual-tree complex wavelet packet transform and ICA[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(3):513-518. (in Chinese)

[12]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London, Series A, 1998,454：903-995.

[13]Huang N E, Wu Z. A review on Hilbert-Huang transform：method and its applications to geophysical studies[J]. Reviews of Geophysics, 2008,46:1-23.

[14]Xu Yuesheng, Zhang Haizhang. Recent mathematical developments on empirical mode decomposition[J]. Advances in Adaptive Data Analysis, 2009，1(4)：681-702.

[15]Dragomiretskiy K, Zosso D. Variational mode decomposition [J]. IEEE Transactions on Signal Processing, 2014,62(3):531-544.

[16]Mohanty S, Gupta K K, Raju K S. Comparative study between VMD and EMD in bearing fault diagnosis[C]∥Proceedingsof the IEEE 9th International Conference on Industrialand Information Systems (ICIIS′14).Gwalior, India:[s.n.], 2014:1-6.

[17]Wang Y, Markert R, Xiang J, et al. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system[J]. Mechanical Systems and Signal Processing, 2015,60:243-251.

[18]Gilles J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013,61(16):3999-4010.

[19]Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009,1(1):1-41.

[20]唐贵基,王晓龙.参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J].西安交通大学学报,2015,49(5):73-81.

Tang Guiji, Wang Xiaolong. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J]. Journal of Xi′an Jiaotong University, 2015,49(5):73-81. (in Chinese)

[21]Chen Weiting, Wang Zhihong, Xie Hongbo, et al. Characterization of surface EMG signal based on fuzzy entropy[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2007,15(2):266-272.

[22]Chen Weiting, Zhuang Jun, Yu Wangxin, et al. Measuring complexity using FuzzyEn, ApEn, and SampEn[J]. Medical Engineering & Physics, 2009,31(1):61-68.

10.16450/j.cnki.issn.1004-6801.2017.03.029

国家自然科学基金资助项目(51505002)；安徽省高校自然科学研究重点资助项目(KJ2015A080)；研究生创新研究基金资助项目(2016062)

2016-06-15；

2016-10-27

TN911.7； TH165.3

姜战伟，男，1990年5月生，硕士生。主要研究方向为动态信号处理和机械故障诊断等。曾发表《VMD based adaptive multiscale fuzzy entropy and its application to rolling bearing fault diagnosis》(《Sensing Technology》 (ICST) 2016 10th International Conference on IEEE)等论文。 E-mail:jzwptt666888@gmail.com