数学复习中的分类归纳

温红梅

（山西省翼城县汇丰学校）

对于中学生来说，数学作为一门基础学科，尤为重要。随着翼城县教育科技文化局开展的教学研究活动的广泛推进，作为汇丰学校一名教师，收益不少。认识到“数学没有新课，新课就是复习课”，也就是说数学知识点很简单，但是简单的知识点却能变换出形形色色的不同习题。因此，数学难学点在于利用知识点灵活地解决问题，相反大多数人信“熟能生巧”，大搞题海战术，虽能有效提高解决问题的能力，但却是非常的辛苦，更有一些学生因为单纯做题，缺乏思考，虽夜夜苦熬做题，却收效甚微，苦不堪言。下面我就几个例题来说明我所说的教学方法。

一、用转化思想，做透基础习题

将未知解法或难以解决的问题，通过观察、分析、类比、联想等思想的过程，选择运用数学的方法进行交换，除简单的数学基础问题外，每个数学问题的解决都是通过转化为已知的问题实现的，转化思想是解决数学问题的根本思想，解题的过程实际上就是一步步转化的过程，数学中的转化比比皆是，如未知向已知转化，复杂问题向简单问题转化，空间向平面的转化，高维向低维转化，多元向一元转化，高次向低次转化，函数与方程的转化，无限向有限的转化等，都是转化思想的体现。

做好基础习题达到熟练的程度，扎实地掌握基础知识、基本技能和基本方法是转化的基础；丰富的联想，机敏细微的观察、比较、类比是实现转化的桥梁；培养训练自己自觉的转化意识需要对定理、公式、法则有本质上的深刻理解和对典型习题的总结和提炼，要积极主动且有意识地去发现事物之间的本质联系。

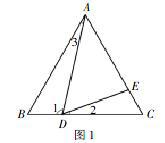
例1.如图1，在边长为9的等边三角形ABC中，BD=3，∠ADE=60°，求AE的长。

这个习题应该算是一个较为简单的习题了，本题中由于∠B=∠C=∠ADE=60°，可以得出∠1+∠2=120°，又∠1+∠3=120°，进而推到∠2=∠3，△ABD∽△DCE，最终利用相似三角形的性质解决问题，对于这类基础性习题我们就应当掌握定理概念一样，从解决思路方法上牢固掌握。

二、用分类思想，讨论归纳方法

数学问题比较复杂时，有时可以将其分割成若干个小问题或一系列步骤，从而通过问题的局部突破来实现整体解决，正确应用分类思想，是完整接替的基础。而在学业考试中，分类思想也贯穿其中，命题者经常利用分类讨论题来加大试卷的区分度，很多压轴题也都设计分类讨论。在我校数学教研组讨论时，初二（8）班的张老师体会是：我们常常需要根据研究队形性质的差异，分不同情况进行解决，这种分类思考的方法是一种重要的数学思想方法的解题策略，掌握分类的方法，领会其实质，对于加深基础知识的理解，提高解决问题的能力十分重要。初三（3）班的李教师体会是：数形结合思想方法是我在教学中常用的思想方法。数是形的抽象概括，形是数的直接表现形式，用数形结合的思想解题可分两类：一要利用几何图形直观表示数，它常借用数轴、函数图象等；二要运用数量关系来研究几何图形，常需要建立方程（组）或建立函数关系式等。

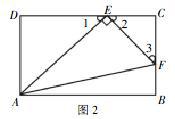
例2.如图2，在矩形ABCD中，EF分别是CD、BC边上的点，若∠AEF=90°，则一定有（ ）。

A.△ADE∽△AEF B.△ECF∽△AEF

C.△ADE∽△ECF D.△AEF∽△ABF

分析，因為∠AEF=90°，所以∠1+∠2=90°，又∠2+∠3=90°，所以∠1=∠3，因此可得出△ADE∽△ECF。

例1和例2两个习题，一个是三角形，另一个是矩形，但是解题方法上不难看出完全相同，因此，我们可将这两种习题归为一类，图形特点为在同一条直线上分布有三个相同角，最终结果它有两个相似三角形，最终利用相似解决问题。

三、用观察思想、拓展图象信息

在2017年山西省中考数学研讨会中，我们组总结了以下几点：

（1）图象信息题是指由图象（表）来获取信息，从而达到解题的目的。（2）图象信息题的图象可分两类。一是教材介绍的基本函数图象（如直线、抛物线、双曲线）；二是不同的习题描绘的不规则图象（如折线型、统计图表等）。这种题型一般是由图象给出的数据信息，探求两个变量之间的关系，进行数、形之间的互换。（3）图象信息题大致有三类：基本概念类、基础综合类和压轴综合类，题型可涉及选择等，迷惑性很大。（4）解图象信息题的关键是“识图”和“用图”，解这类题的步骤是：①观察图象，获取有效信息；②对已获信息进行理性分析，理清各变量之间的关系；③选择适当的数学工具，恰当解决问题。（5）图象信息题的解决方法是观察图象，从图象给我们提供的已知条件了解，认真分析，由图象信息分析出有关函数解析式，揭示问题的数学关系和本质属性，找到了解题的途径。

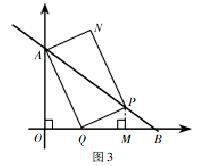
例3.如图3，直线y=-3/4x+3与y轴交于点A，与x轴交于点B，点P从点B出发，以每秒1个单位长度的速度沿BA边向终点A运动，同时点Q以相同的速度从坐标原点出发沿OB边向终点B运动，设点P运动的时间为t。

在点P、Q运动的过程中，是否存在点N，便得以点AP、QN为顶点的四边形为矩形？若存在，求t的值，并直接写出N的坐标，若不存在，请说明理由。

这道题需要分类讨论，就有一定难度了，这道题有三种情况，其中一种如图，所构建的图形是否似曾相识呢？

再伟大的建筑也是由一砖一瓦建起来的，再复杂的习题也是由基础题构建而成的。只要我们基础扎实，肯抽象归纳，再复杂的习题也会迎刃而解的。

编辑 温雪莲