最优电动车发展规划的探究

胡 伟

（中南大学交通运输工程学院，湖南长沙 410075）

1 介绍

1.1 背景

随着全球能源危机的不断加深，石油资源的日趋枯竭以及大气污染、全球气温上升的危害加剧，各国政府及汽车企业普遍认识到节能和减排是未来汽车技术发展的主攻方向。与此同时，受环境和经济的影响，消费者也开始转向电动汽车。电动汽车作为新一代的交通工具，在节能减排、减少人类对传统化石能源的依赖方面具备传统汽车不可比拟的优势。

与传统汽车相比，电动汽车具有以下优点:

①零排放或近似零排放。

②减少了机油泄露带来的水污染。

③降低了温室气体的排放。

④提高了燃油经济性。

⑤提高了发动机燃烧效率。

⑥运行平稳、无噪声。

基于以上优点，在世界范围内很多公司开始进行电动汽车的研究，目前水平较为先进的是美国的特斯拉公司。在政府的鼓励和技术不断成熟趋势的影响下，电动汽车的市场也会越来越大，但与此同时电动汽车开发者需要考虑的问题也越来越多。充电站的设计（包括数量，地域分布，充电器的数量及地域差异）成为影响未来电动汽车市场占有率和发展程度重要因素。所以充电站最终网络的设计也是国家在这一重要转型期中需要着重解决的难题。

本问题所研究的方向就是根据各个国家的不同情况来制定一个最适合其国电动汽车（只关注个人乘用车）推广过渡的计划，包括确定充电站网络的构架设计等，并分析各种实际因素会对电动汽车的日益普及的影响及影响方式。

1.2 概述

首先对于我们要解决的问题，我们找到了这几个关键点：

①由于新能源汽车历史较短，时间维度上的数据较少。

②任务中需要我们做未来的计划，那么时间是相对重要因素。

③我们需要初步寻找数据为，地域数据、人口数据、财富数据、车辆数据。

④充电站的分布影响因数。

⑤若电动汽车计划施行于不同国家，什么因素会造成不同影响。

⑥给一个国家进行电动汽车的从无到有的计划，如何找到影响因素并量化数据。

⑦如何修改模型让它适合更多国家及城市使用。

⑧通过我们以上讨论，我们确定了接下来做解决方案的四个步骤：

首先把寻获的所以数据进行初始化处理：数据来源的可靠性分析、数据的完整性分析、数据规范化处理。

第二，对不同模型，用PCA方法对影响因素进行筛选。

第三，大致确定模型方向。

第一部分：采用预测模型预测特斯拉是否在走美国的全电趋势，拟合并预测出未来几年电桩数量图片；根据农村，城市，郊区对电桩数量分配的影响做模糊综合评价进行电桩数量分配。

第二部分：Task2a，分配方法采用类比美国电桩分配方式，预测方法，并修正模型，规划方法采用基于障碍的空间聚类分析和目标规划模型，并采用粒子群启发式算法求解。Task2b，采用层次分析法解决，task2c，采用竞争-logstic 模型预测电车发展时间表。

第三：模型进一步分析

1.3 模型假设

①车辆行驶里程与充电费用是线性关系。

②需求区已经科学划分，几何的中心位置表示其充电需求点。

③具有充电需求的电车聚集于需求区中心位置。

④对于特定的一段充电时间区间，同一个中心点的位置的用户，都只能选择一个同一充电点。

⑤假设候选站已经给出，我们目的是进行候选站选址优化。

⑥假设每个用户充电都充满为止。

⑦燃油汽车、电动汽车都是一种固定车型。

⑧电价，油价不随时间变化。

⑨假设候选充电站都建在平原上。

⑩影响因素不包括自然灾害影响。

⑪不受天气、海拔的影响。

1.4 变量符号

1.4.1 第一部分 计算电桩在美国的数量以及其在农村，郊区，市区的分布情况

Q 不同地域充电站的数量N 不同地域充电站的需求电量K 备用系数，查资料取值为1.25 T 充电站工作时间，查资料后取值为10h A车辆数量D人口数量G人均GDP

1.4.2 第二部分 针对韩国Super charge和目的地充电方式的选址规划问题分析

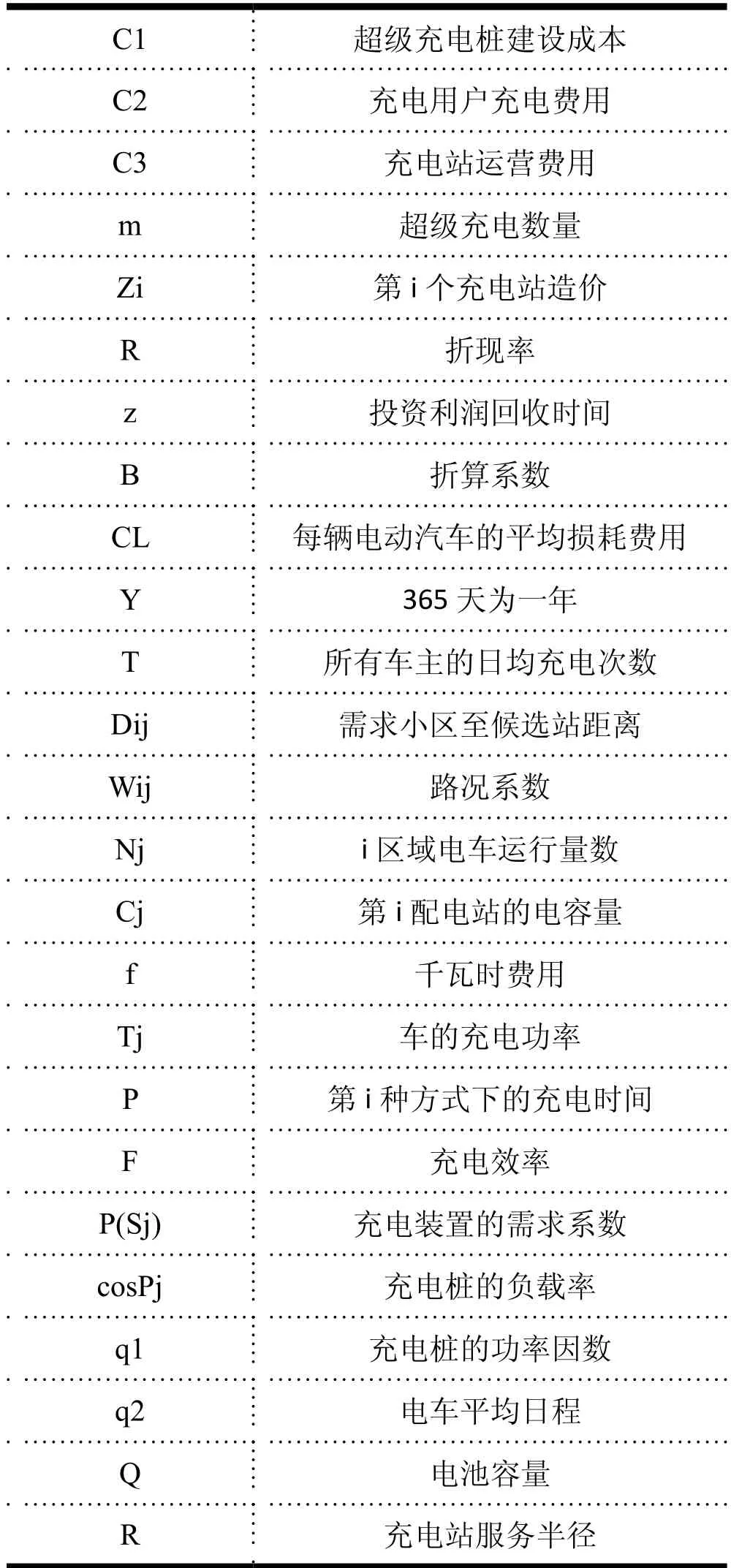
C1 超级充电桩建设成本C2 充电用户充电费用C3 充电站运营费用m超级充电数量Zi 第i个充电站造价R折现率z投资利润回收时间B折算系数CL 每辆电动汽车的平均损耗费用Y 365天为一年T所有车主的日均充电次数Dij 需求小区至候选站距离Wij 路况系数Nj i区域电车运行量数Cj 第i配电站的电容量f千瓦时费用Tj 车的充电功率P第i种方式下的充电时间F充电效率P(Sj) 充电装置的需求系数cosPj 充电桩的负载率q1 充电桩的功率因数q2 电车平均日程Q电池容量R充电站服务半径

1.4.3 第二部分 电动汽车全面发展时间表

r1 每年燃油汽车市场投放的固有增长率r2 每年电动汽车市场投放的固有增长率δ1/δ2 每年单位燃油汽车与电动汽车的百公里平均使用费用比x1 燃油汽车数量x2 电动汽车数量N1 燃油汽车市场饱和数量N2 电动汽车市场饱和数量P市场占有率

1.5 第一部分

1.5.1 第一部分a(探究特斯拉是否走上全电趋势)

1.5.1.1 问题分析

首先我们探究特斯拉是否走上全电趋势，因为灰度预测对较少数据可以进行有力预测，所以我们首先对特斯拉电动车在轻型汽车（car+light trunk）市场占有率进行了等维灰数递补预测，接下来对充电桩数量在占比的持续增加下进行插值拟合。若预测合理，拟合效果良好，则说明特斯拉在美国汽车完全切换到电车（90%）,它的里程上有较强趋势。因为电动车占有率前期可能是S型序列，后期逐渐趋于S曲线。由于前期市场占率较小，所以我们采用指数型GM我们前期建立等维灰数递补GM（1,1）模型。

市场有率-灰数预测GM（1,1）模型 它能够对较少数据，甚至4个数据，只要能通过检验那么都能进行预测。

1.5.1.2 模型建立

数据检验和处理

为了保证模型的可行，我们对2013-2017年的特斯拉市场占有率数据列，作必要的检验处理。

级比检验

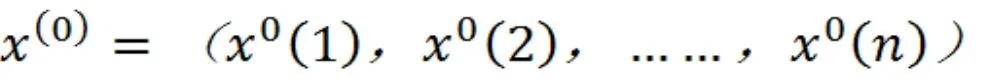
级比：

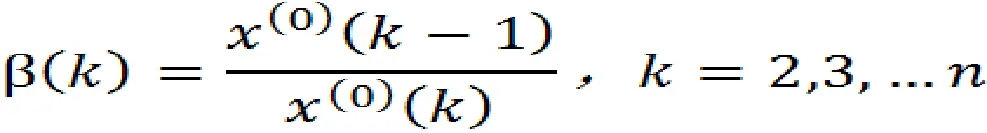
若每一个级比β(k)都落在可容覆盖Θ

区间内，则序列x(0)可以进行模型的预测。否则需要通过变换处理，使其处于有效区间才能进行下一步。

光滑度检验

设序列为非负数据列，只要递减函数，则序列为光滑离散序列。

只有这样才可以把序列用于建模。

通过检验之后

为了弱化原始数据的随机度, 提高数据的平稳度,对原始序列

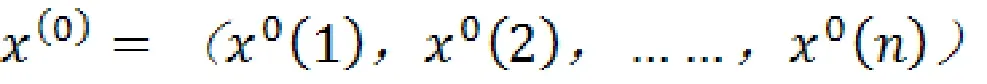
一次累加得到新的数据序列

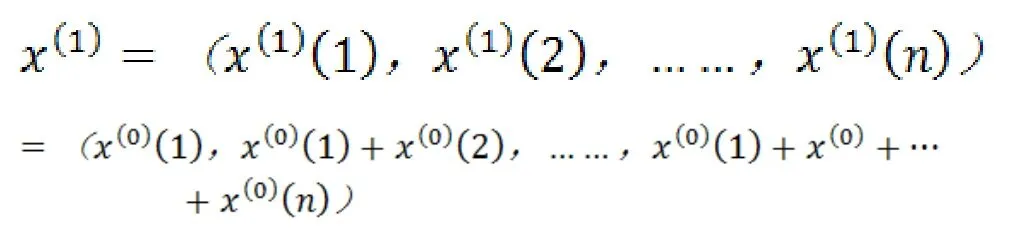
式中

模型精度检验

残差：

相对误差：

计算小误差概率w和方差比h

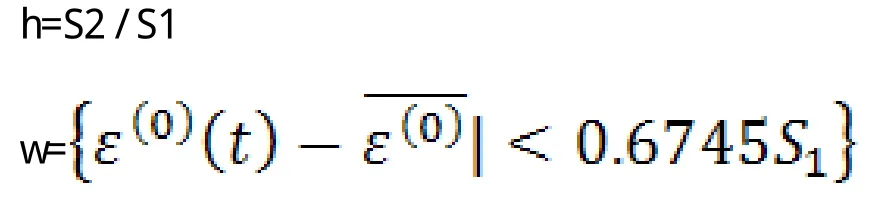
若 h和 w都在允许的范围之内 ,由表一判断就可以用模型进行预测。否则 , 需要通过分析残差序列对模型进行修正 , 灰色预测常用的修正方法有残差序列建模法和周期分析法两种。

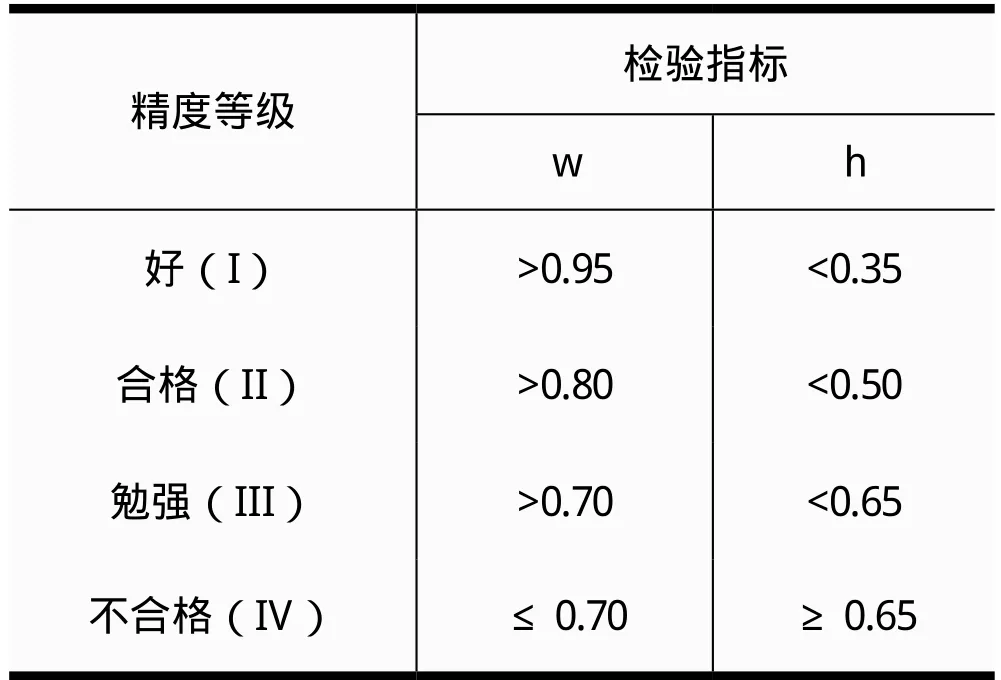
表一 GM(1,1模型检验标准)

1.5.1.3 模型求解

特斯拉汽车市场占有率数据

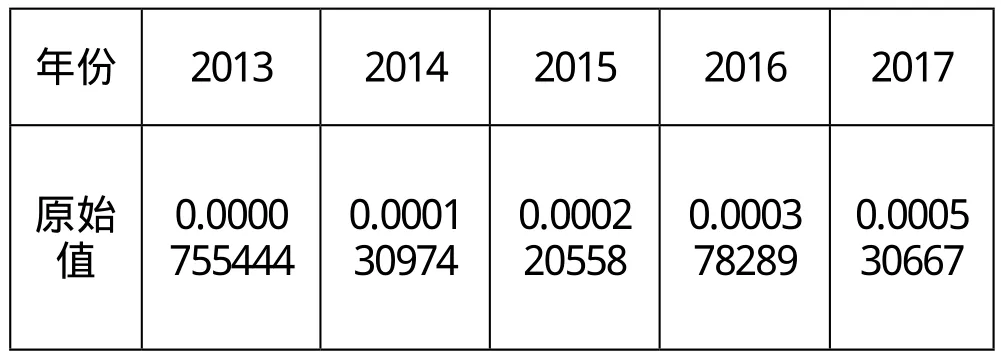
年份 2013 2014 2015 2016 2017原始值0.0000 755444 0.0001 30974 0.0002 20558 0.0003 78289 0.0005 30667

级比检验：落在都落在可容覆盖0.7129）内。

光滑度检验：

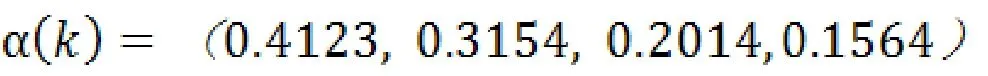
递减表明可以用于GM(1,1)模型。

通过预测得到第一次预测结果

年份 原始值 预测值 残差 相对误差级比偏差2013 0.0000 755444 0.000 0755 0 0 0 2014 0.0001 30974 0.000 1459-0.000 01493 0.114 0.1066 2015 0.0002 20558 0.000 2244-0.000 00389 0.0176 0.0805 2016 0.0003 78289 0.000 3453 0.0000 3302 0.0873 0.097 2017 0.0005 30667 0.000 5311-0.000 00045 0.0008-0.1041

时间响应函数

模型等级为好（I），小误差概率w为1,模型优良。

1.5.1.4 模型改进

由于GM(1,1)预测第一个数据最好，若进行长期预测，一方面，误差逐渐下降，精度降低；另一方面系统变化数据不能及时反应。那么我们每一次预测值放在上一次数据末尾，把第一个数据去掉。构成一个S位不变的序列这个S维的

G（1,1）模型进行计算，得到第二个预测值。那么重复保持S维，数据平滑下去的不断进行新的GM（1,1）预测,这样的方法即为等维灰数递补模型。它的优点在于能够利用新的预测值，能提高灰区间的白化度，并且这个模型在进行不断的修正中，所以预测结果越来越合理、精确。

改进后的预测

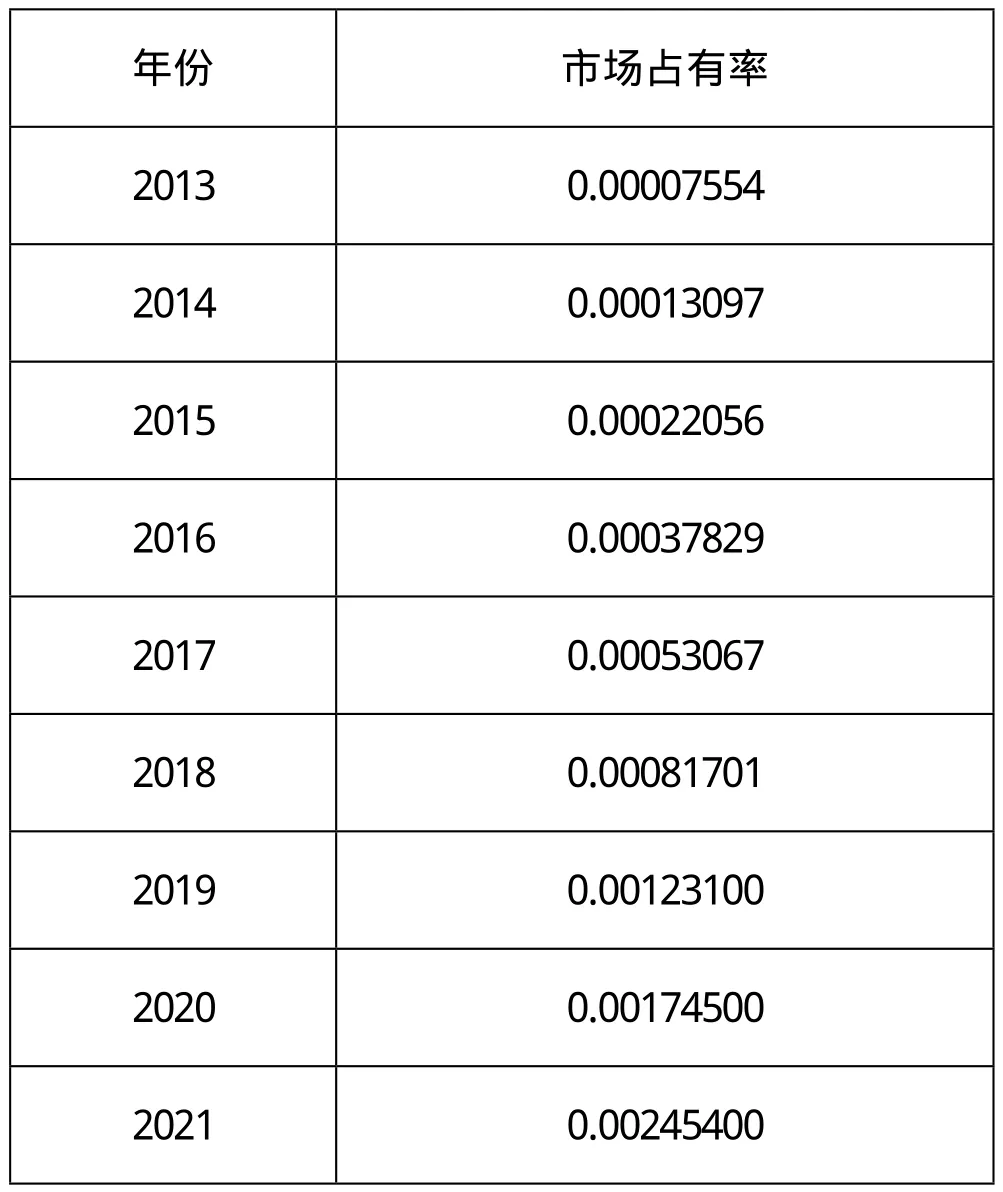
表2 特斯拉市场占有率未来四年的预测

电动汽车市场占有量预测

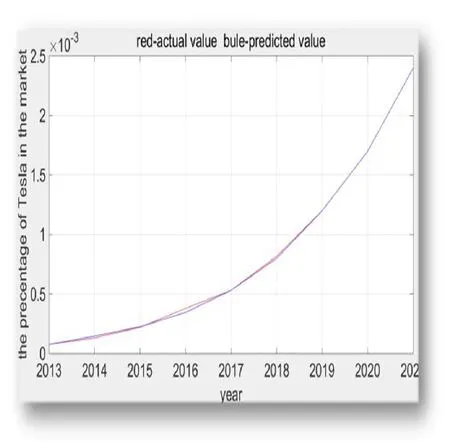
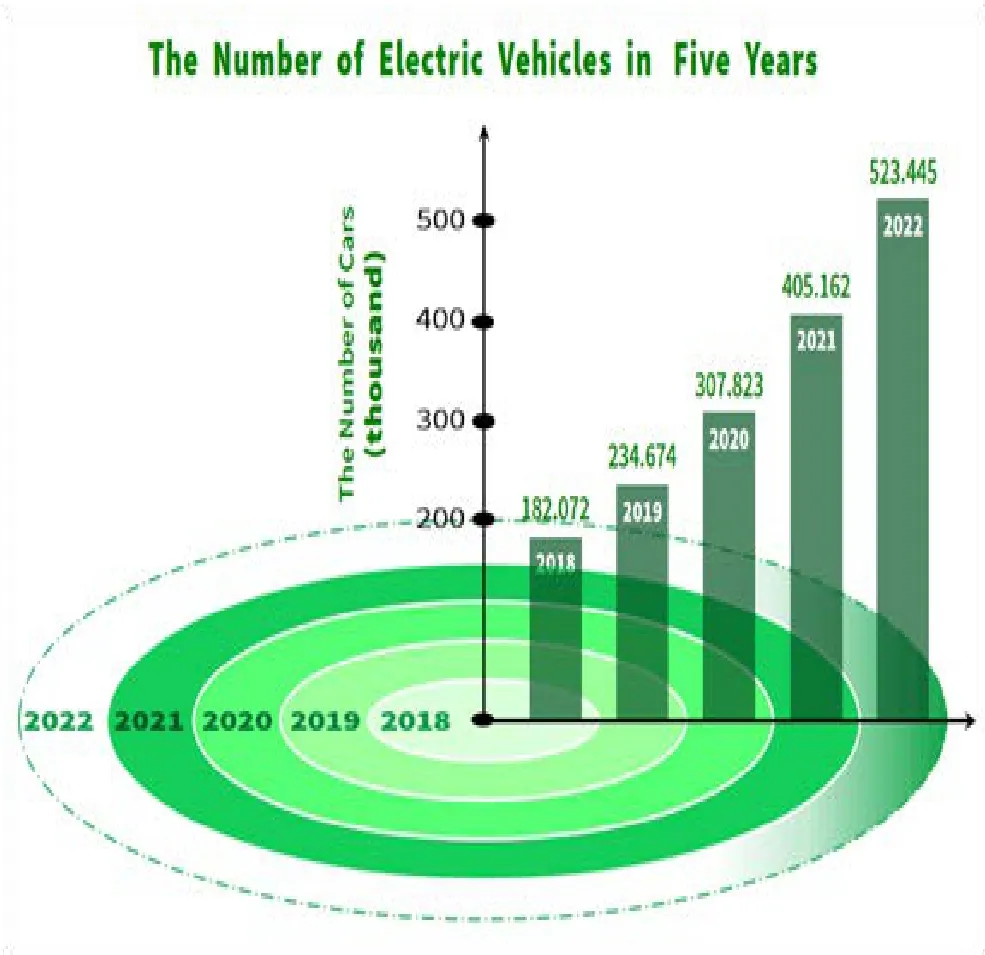
1.5. 2 第一部分b（求出美国需要的充电桩数量，同时探究出充电桩在农村，郊区，城市所占的百分比)

1.5.2.1 问题分析

求出美国需要的充电桩数量，同时探究出充电桩在农村，郊区，城市所占的百分比。我们首先查询资料，拟合出特斯拉销量随时间变化的函数关系，其次拟合出特斯拉汽在所有汽车中占比随时间变化的规律。最后根据这两个函数关系可以得出充电桩数量与特斯拉汽在所有汽车中占比的关系。当占比为一时即可求出充电桩数量。

1.5.2.2 数据处理

确定特斯拉销量随时间的变化的变化规律

特斯拉年销量

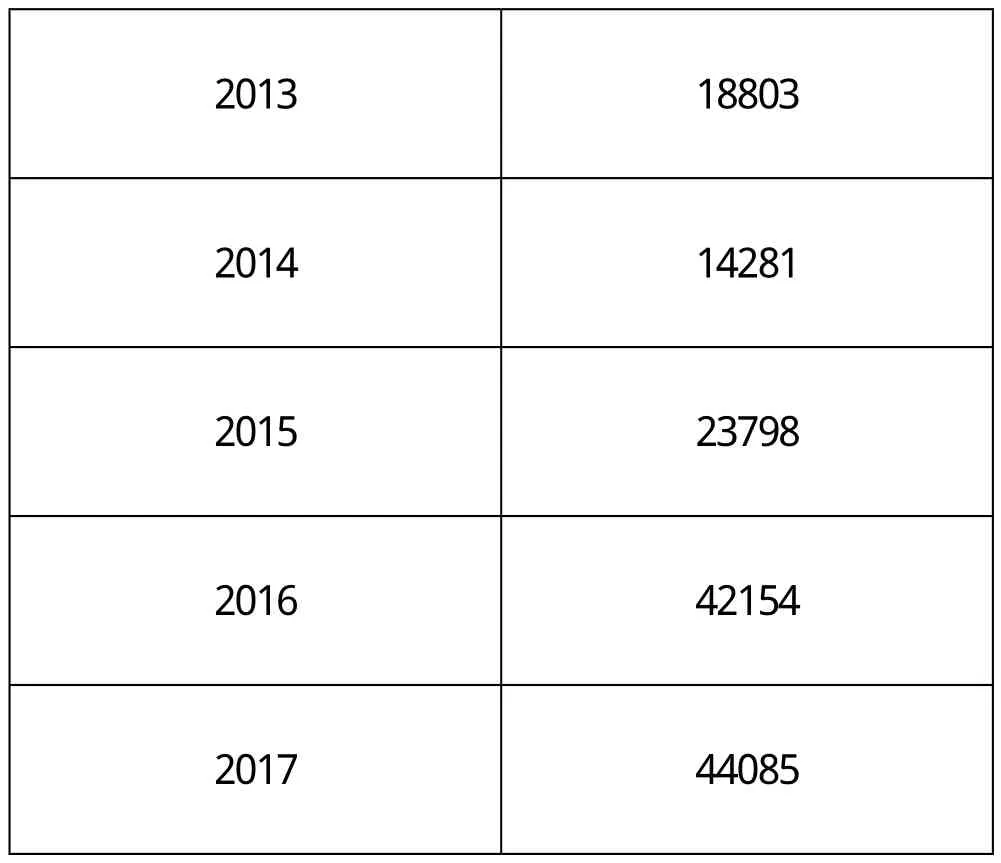
2013 18803 2014 14281 2015 23798 2016 42154 2017 44085

确定特斯拉在汽车总量中占比随时间的变化

美国汽车总量

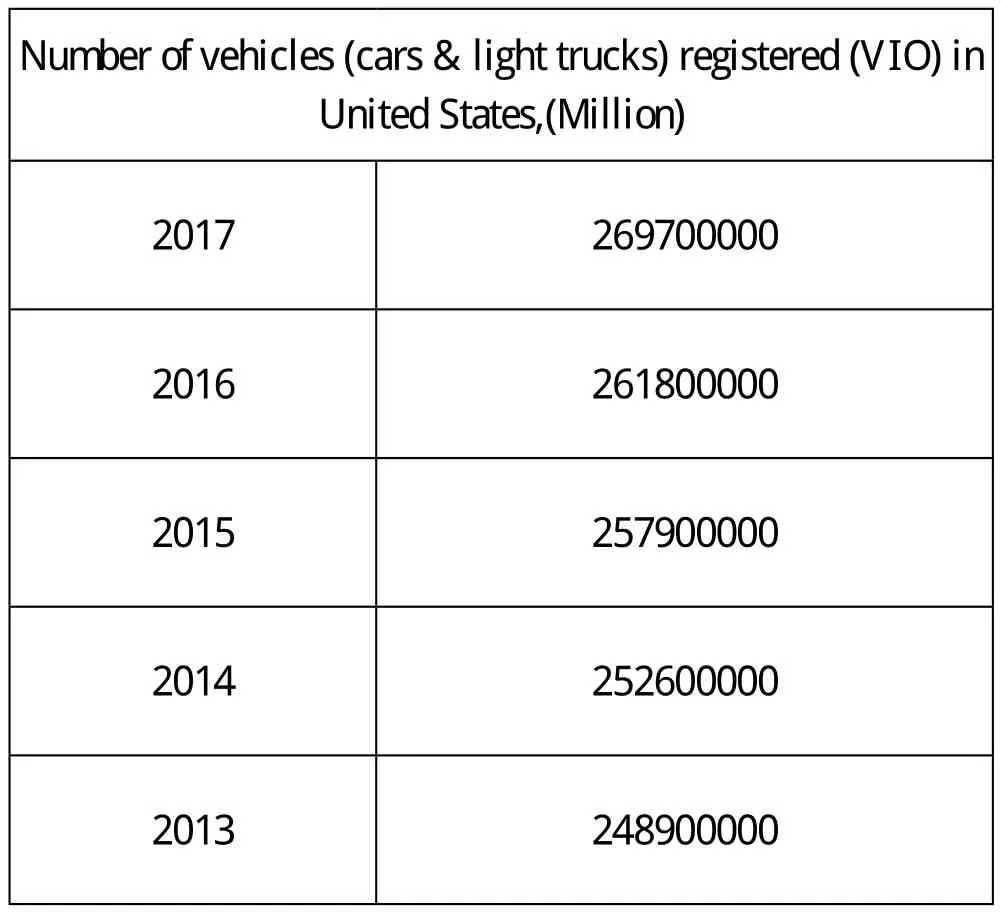
Number of vehicles (cars & light trucks) registered (VIO) in United States,(Million)2017 269700000 2016 261800000 2015 257900000 2014 252600000 2013 248900000

特斯拉占比，每年特斯拉的车辆数是之前几年销售量的累加

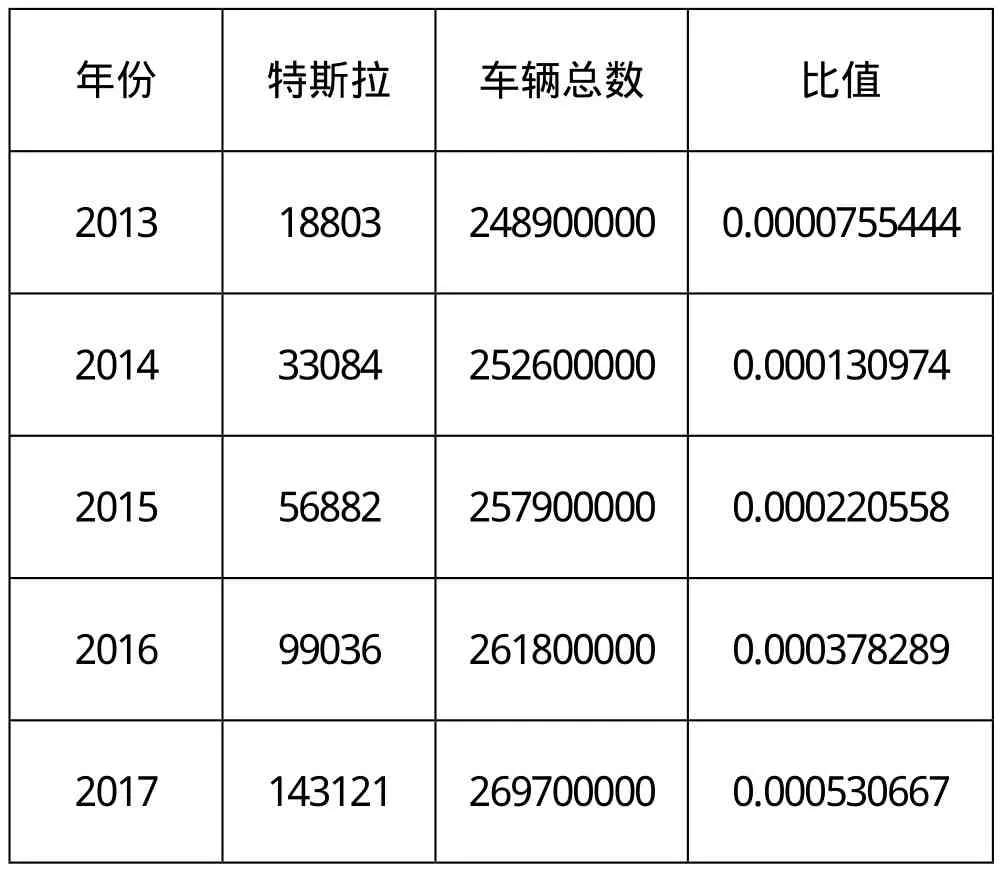
年份 特斯拉 车辆总数 比值2013 18803 248900000 0.0000755444 2014 33084 252600000 0.000130974 2015 56882 257900000 0.000220558 2016 99036 261800000 0.000378289 2017 143121 269700000 0.000530667

确定充电桩数量随时间变化的图

对应的充电桩数量为

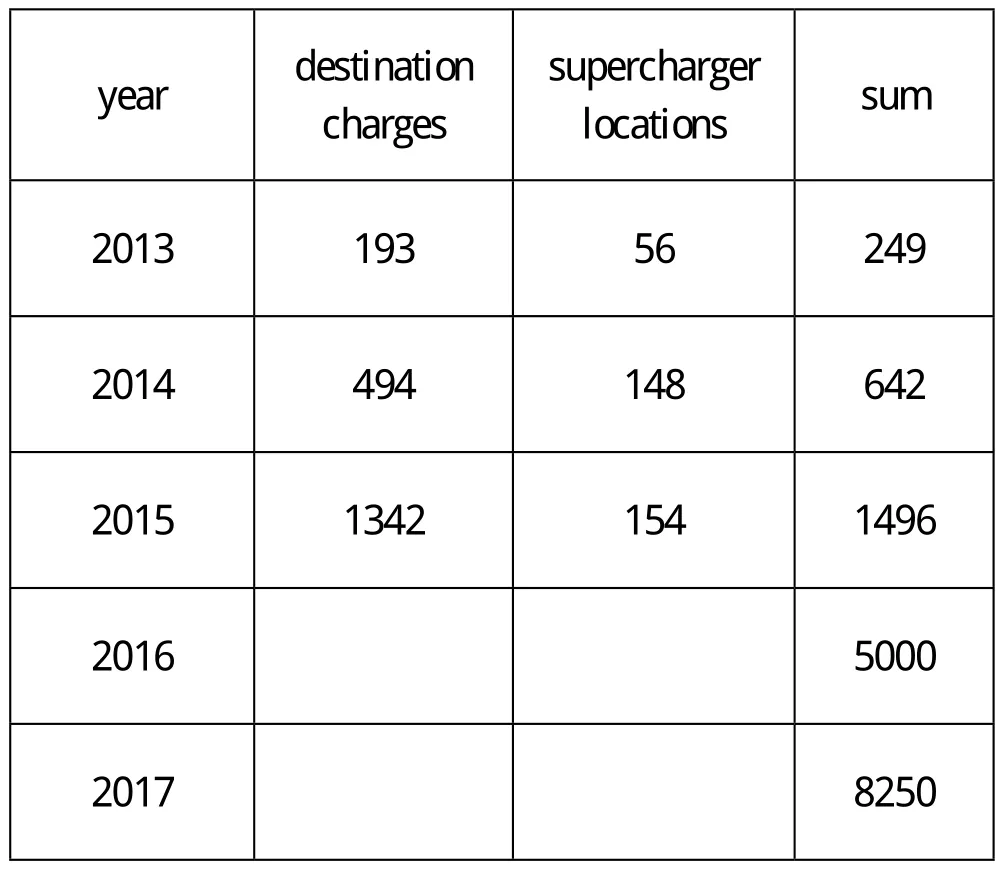
year destination charges supercharger locations sum 2013 193 56 249 2014 494 148 642 2015 1342 154 1496 2016 5000 2017 8250

1.5.2.5 模型建立

结合以上数据，利用matlab编程，找出电动汽车占比与充电桩数量的关系

Linear model Poly1:

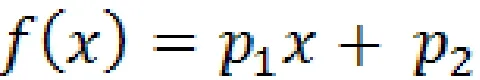
Coefficients (with 95% confidence bounds):

P1=1.813×107

P2=-1717

Goodness of fit:

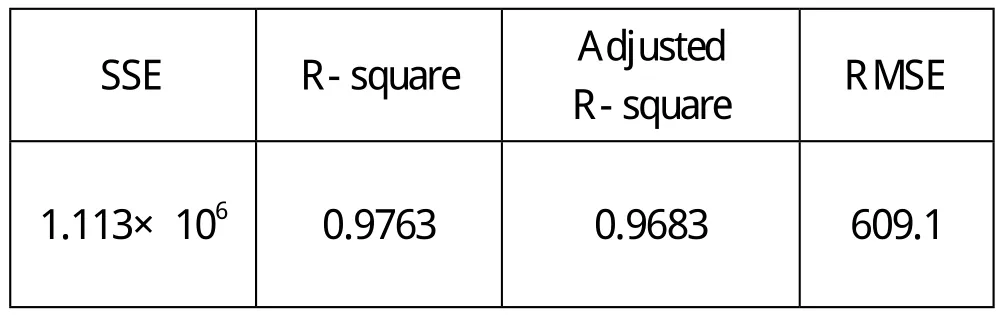
SSE R-square Adjusted R-square RMSE 1.113×106 0.9763 0.9683 609.1

所以方程为

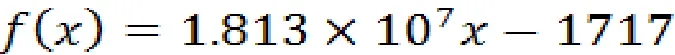
1.5.2.6 模型的求解

当完全转为电动汽车后，电动汽车占比为1

把X=1代入

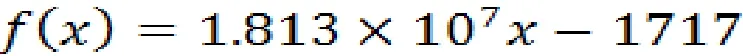
f(x)= 18128283 需要1812万个充电桩

1.5.3 第一部分c(探究充电桩在不同地域的分布情况)

1.5.3.1 问题分析

探究数量分布时，首先查询资料得出充电桩数量计算的方程，而后加入人均GDP，车辆数量，人口数量等权重因素对模型进行改进，通过量化影响因素求出权重。确定改进后的计算方程，代入农村，郊区和城市后的数据后求出分布百分比。

1.5.3.2 数据处理

要求不同地域充电站的需求电量要考虑车辆数量w1，考虑人口分布情况w2，人均GDPw3，本文选取了这三个因素作为自变量。量化影响因素。

充电站2013，2014,2015年的实际数量249,642,1496

通过探究充电桩数量随时间变化的方程计算出电桩数量值为250 ，640，2000

列方程组

249=250(w1+w2+w3）

642=640(1.1w1+1.1w2+w3)

1400=2000(1.1w1+w2+1.1w3)

第一个方程代表三个系数影响因素一样为参照组

matlab解方程组解得

W1= 68.9320=69

W2=-17.9844=18

W3=-1.9650=2

进一步求得这三个因素所占的权重

W1=69/(69+18+2)=0.77

W2=18/(69+18+2)=0.20

W3=2/(69+18+2)=0.03

1.5.3.3 模型建立

参考文献后建立如下模型，用以下公式求得充电站的数量。充电站的数量和容量是一定的，因为所有充电站提供的总电量是一定的。

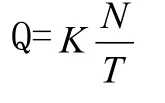
加入车辆数量w1，考虑人口分布情况w2，人均GDPw3作为影响因素，建立不同地域充电站数量需求的影响因素。N=W1*A+W2*D+W3*G

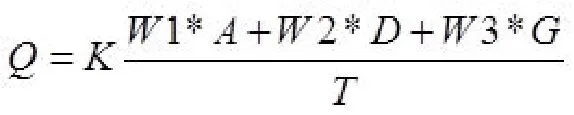
1.5.3.4 模型求解

通过收集资料可知

美国汽车分布,人口分布和美国人均GDP

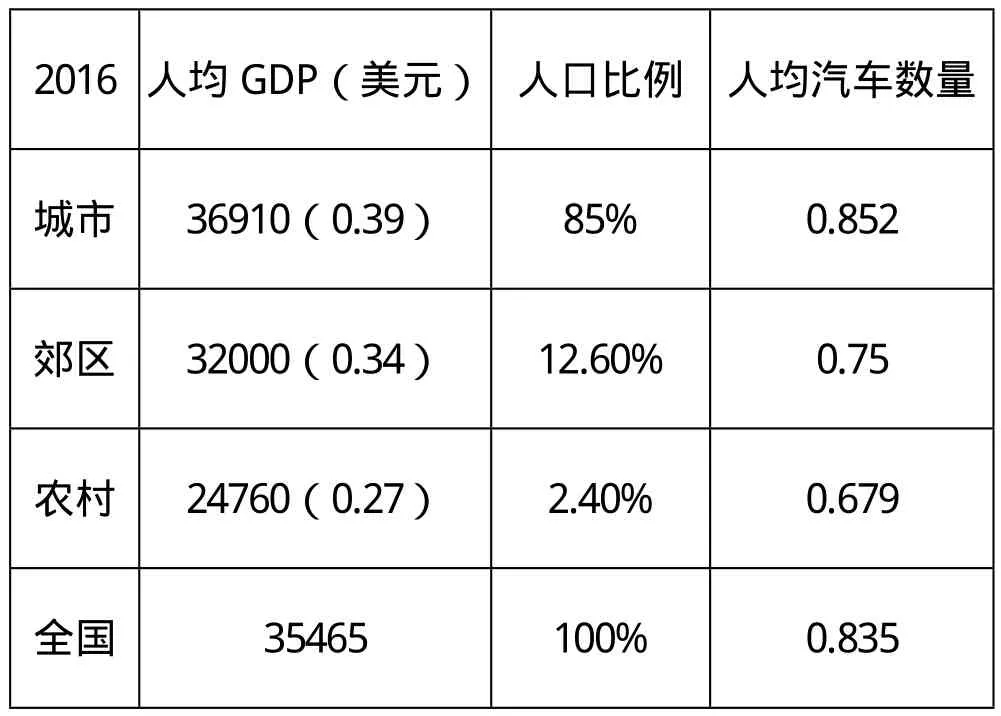
2016人均GDP（美元） 人口比例 人均汽车数量城市 36910（0.39） 85% 0.852郊区 32000（0.34） 12.60% 0.75农村 24760（0.27） 2.40% 0.679全国 35465 100% 0.835

带入相关数据求得城市，郊区，农村的比值

城市0.77*0.825+ 0.20*0.85+0.03*0.39=0.8170

郊区0.77*0.75+ 0.20*0.1260+ 0.03*0.34=0.6129

农村0.77*0.679+0.20*0.024+ 0.03*0.27=0.5357

城市：郊区：农村=0.817:0.6129:0.5357 1.9656

求得充电桩在城市，郊区，农村中的比例分别为41% 31% 28%。

1.6 第二部分

1.6.1 问题分析

1.6.1.1 针对最佳充电站数量的预测，以及如何分配、如何规划有以下几个思路

1.6.1.1.1分配和最佳电站数量，我们选择了韩国作为考虑对象，对于韩国未来充电站总数的预估，我们以美国和韩国的已有数据平均人口数、人均GDP、人均车辆拥有数为类比因子，进行移植。

1.6.1.1.2选址规划问题，我们以韩国某县为例子

①关于超级充电桩的建设，我们考虑到某县的具体情况，在实际的建模过程中，我们考虑了一下因素：土地征收情况，候选站地理情况，总体的规划与协调，充电桩的容量的局限性，每天的服务车辆数也不尽相同。在我们的解决方案中，假设大田县投建局还会考虑实际情况，以我们的方案作参考。我们通过成本的多目标规划建模，求解过程采用粒子群算法求解；

i．候选站中成本最低的超级充电站，

ii．把不同的超级充电站进行合理分配给不同需求的充电小区

②关于目的地式充电站的建立，基于人们以此方式的充电位置主要位于人群聚居的地方，要么是工作地点，要么是生活小区，并且实际生活中会存在公园、湖泊、铁路，建筑等障碍。所以我们选取了大田县的市区一脚，通过 K-Medoids带障碍约束空间聚类分析模型，找出具有最大服务效应的中心，以此中心作为目的地电桩的建设。

1.6.1.2 确定充电站的发展模型

本部分将探求所在国家的充电网络的发展过程，确定农村充电器，郊区充电器，城市充电器的发展顺序。为了评估发展顺序，建立一个总效益函数，通过层次分析法确定消息函数的权重系数。主要考虑的评估指标有地区人均GFP，地区人均汽车数量，地区人口。以反映充电器的建设效果，在保证效益最大画的基础上，确定发展顺序。

1.6.1.3 电动汽车全面发展时间表

本部分我们将根据我们所选的国家，给出国家电动汽车全面发展的时间表，大致什么时间达到市场占有10%，什么时候30%，什么时后50%，什么时候接近 100%。什么是影响我提出时间表的关键因素？

汽车全面发展的时间预测等价于市场占比关于时间的预估函数的实现。实际上电动汽车和轻型燃油汽车是一个竞争关系，某个意义上可以理解为它们在争夺同一市场空间上的客户资源。当只有电车或者燃油汽车存在时，可以预想它的一个数量演变遵循 LOGISTIC规律。那么要解决此两种汽车竞争情况下数量演变，问题我们想到的方法是汽车竞争-LOGISTIC模型。

1.6.2 模型建立

1.6.2.1 韩国电桩的最佳数量及分配和规划模型

最佳数量的确定及分配模型

①根据任务一中模型再对比和韩国的人口，人均汽车数量，人均GDP确定充电桩数量。

美国最佳充电站数量：fu.s

韩国最佳充电站数量：

运用任务1c中的W系数法，求得Wi i=1,2,3

分配比例

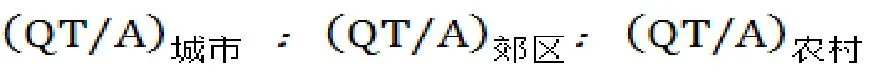
韩国2017年度数据

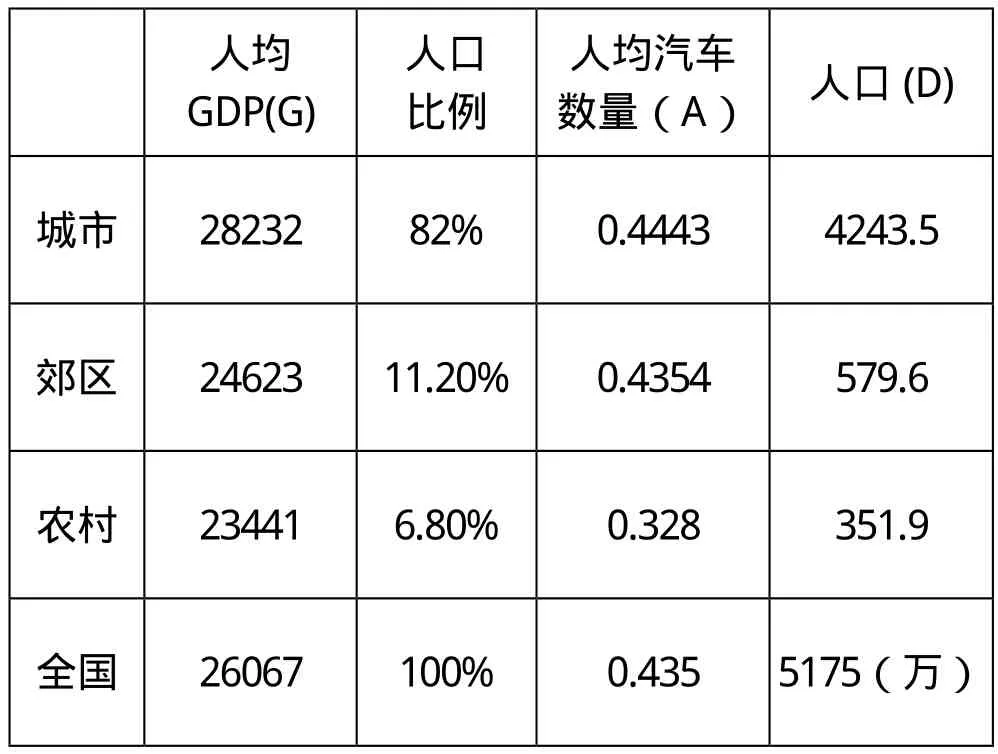
人均GDP(G)人口比例人均汽车数量（A） 人口(D)城市 28232 82% 0.4443 4243.5郊区 24623 11.20% 0.4354 579.6农村 23441 6.80% 0.328 351.9全国 26067 100% 0.435 5175（万）

最佳规划模型

Super charger的布置模型 ----多目标规划 +粒子群法寻找最优布置

①0,1变量

Kj=1表示第i个预选超级充电站被选中，Kj=0则否定；

gij=1表示从 i区域至 j超级充电站充电；gij=0则否定

②集合变量Iij表示从区域i至j充电站的集合

在满足最小需求情况下，用户支出 +建设成本最小的充电站布局规划

目标函数：

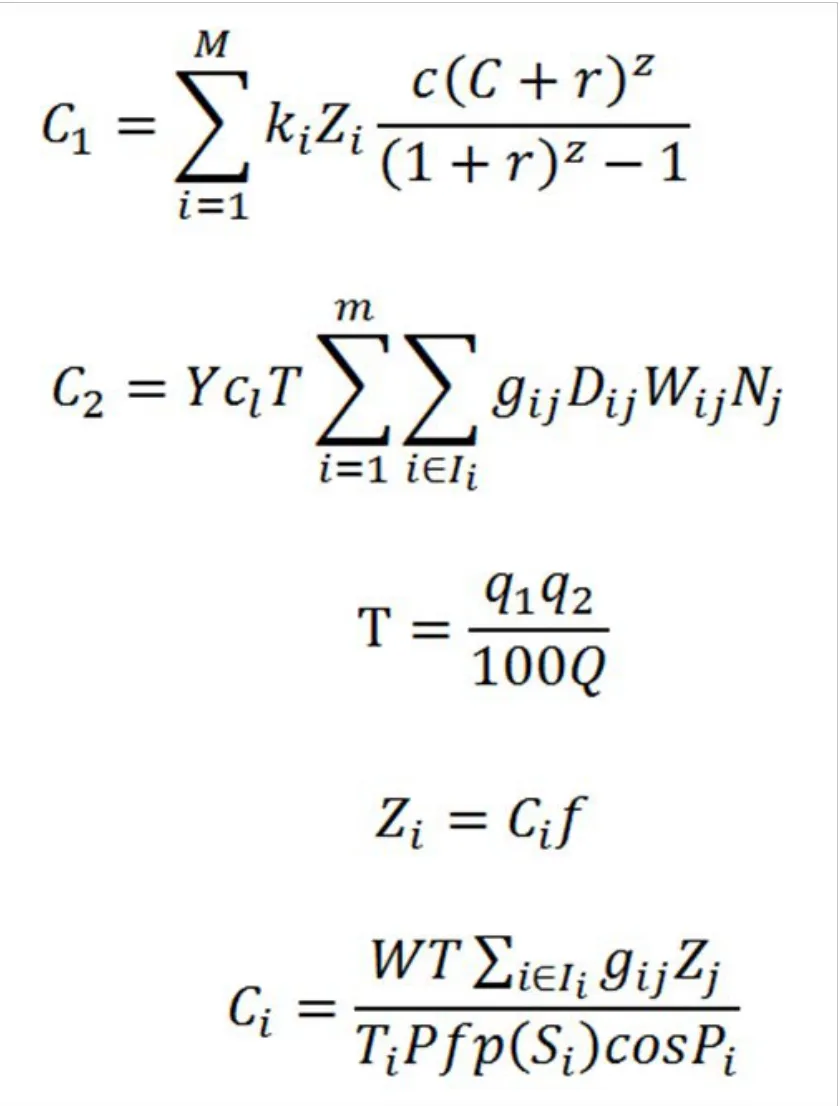
约束条件

充电容量约束：

服务半径约束

对目标函数求解

基于 K-Medoids 带障碍约束空间聚类分析模型（表明引用文献）—固定式电桩布置

首先，数据处理我们首先把原来的空间数据需要处理的所有障碍数据将其叠加为障碍层，把障碍层的矢量数据将其转变为二值格栅数据。我们准备用空间聚类分析，将人口分布位置进行聚类分析。在这里铁路、河流、人工湖作为障碍数据，道路的缓冲区和马路交叉时使用，把它们叠加生成障碍层，产生结果图片为二值栅格的障碍图像文件，如图所示。

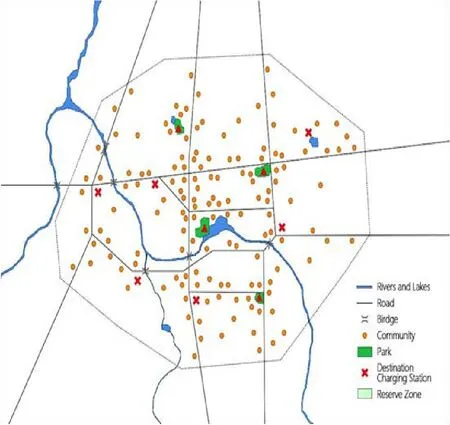
其次建立算法

准则公式

ci是簇 Ci的中心位置，d0（p，ci）为两点的障碍距离。

算法的实现步骤

1. 选初始簇中心点；

2. 对指派对象-给予最近中心点代表的簇；

3. 计算 E0

4.

5. 随机的去选择一个非中心点代替中心点Ci；

6. 每个对象的最近簇的中心进行重新分配；

7. 重新计算E0;

8. 当E0小于CE,形成新的K个簇中心；

最后用MATLAB进行仿真

1.6.2.2 确定充电器安装的发展模型

首先确定一个发展的模型的总评价指标：Z=T1*A+T2*D+T3*G

确定自变量为：便民指数、服务车辆范围、对区域经济发展的带动程度

⑴其次采用层次分析法确定权重因素

现在已经确定有以下3个一级指标：便民指数，服务车辆范围，对区域经济发展的带动程度。

现在要确定这3个指标之间的权重

构建3个指标对比矩阵，形成一个3阶矩阵

Tij=1，元素i与元素j 对上一层次因素的重要性相同；

Tij=3，元素i比元素j 略重要；

Tij=5，元素i比元素j 重要；

Tij=7，元素i比元素j 重要的多；

Tij=9，元素i比元素j 极其重要；

根据政府着重考虑的因素进行专家打分

T1：便民指数

T2：服务车辆范围

T3：对区域经济发展的带动程度

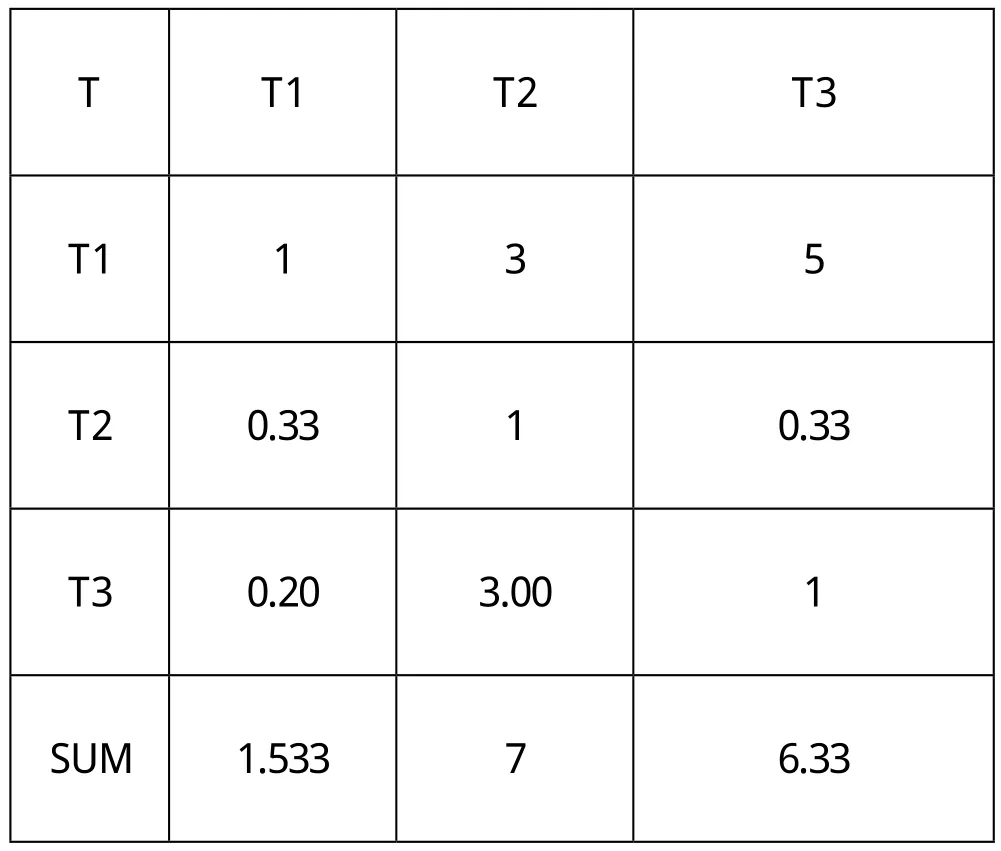
T T1 T2 T3 T1 1 3 5 T2 0.33 1 0.33 T3 0.20 3.00 1 SUM 1.533 7 6.33

归一化处理得出指标的权重，

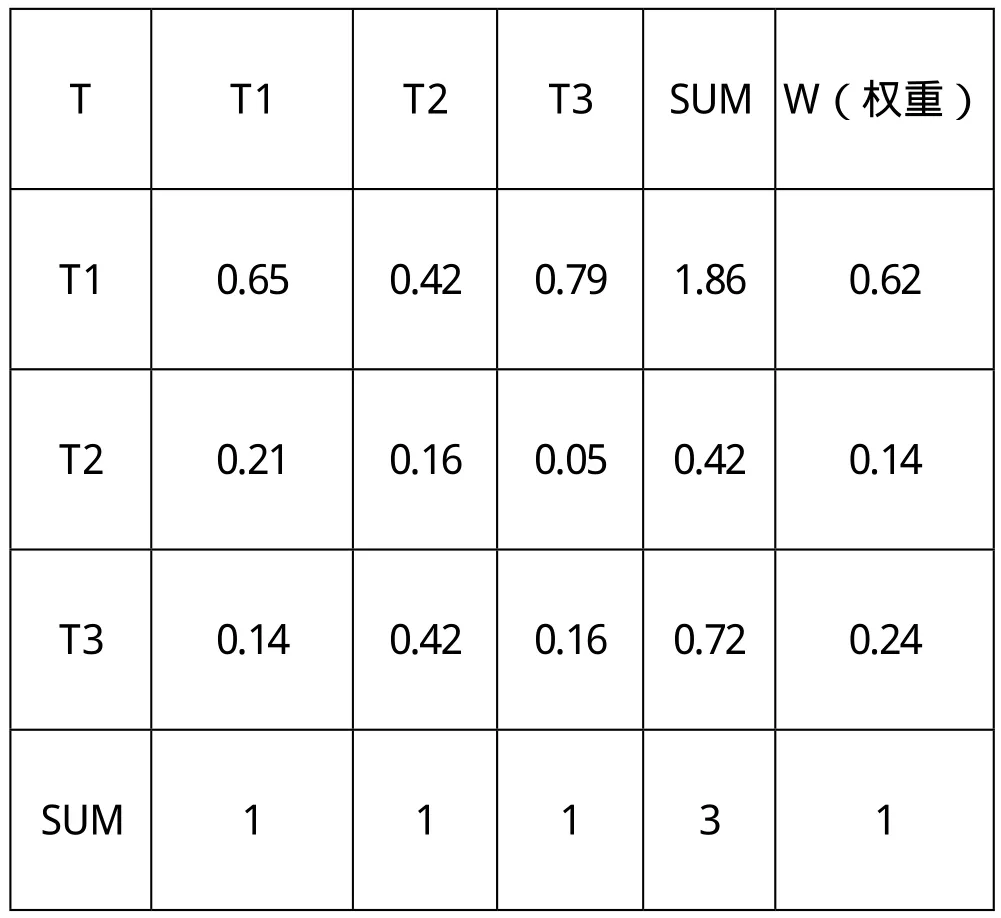
T T1 T2 T3 SUM W（权重）T1 0.65 0.42 0.79 1.86 0.62 T2 0.21 0.16 0.05 0.42 0.14 T3 0.14 0.42 0.16 0.72 0.24 SUM 1 1 1 3 1

建立一个充电器安装后评估效果的效益函数。并确定自变量的权重。

便民指数 (T1) 服务车辆范围 (T2) 对区域经济发展的带动程度(T3)

所以得到总效益Z=0.62*A+0.14*D+0.24*G

1.6.2.3 电动汽车全面发展时间表预测模型

汽车竞争-LOGISTIC模型

对于甲燃油汽车，有

其中表示燃油汽车本身对市场资源的消耗对它本身增长的阻滞作用，表示相对于饱和数量 N1单位燃油汽车的市场消耗（市场总量为 1），当两个类汽车同时出现时，考察电动汽车消耗同一市场资源对燃油汽车的影响，那么合理的在后减去另外一因子，其中表示单位数量燃油汽车消耗的市场资源，是单位电动汽车消耗市场资源的倍，类似的，燃油汽车的存在也影响了电动汽车的增长。

所以有微分方程组：

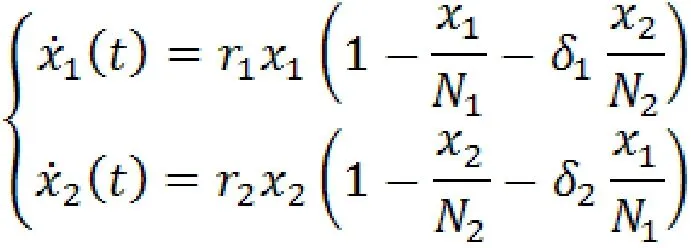
其中δ1与δ2互为倒数关系。

方程组的解，就是随着时间变化电动汽车市场数量和燃油汽车市场数量的规律

对方程两边积分

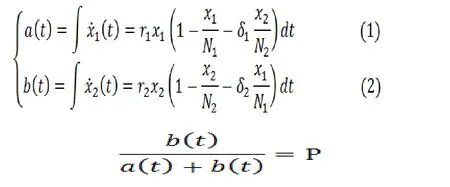
1.6.3 模型求解

1.6.3.1 南韩电桩的最佳数量及分配和规划模型求解

最佳数量的确定及分配模型的求解

南韩最佳充电站数量：S=4530000

城市QT/A=

0.77*0.4443+ 0.20*0.82+0.03*0.37=0.5172

郊区QT/A=

0.77*0.4354+ 0.20*0.1120+ 0.03*0.32=0.3673

农村QT/A=

0.77*0.328+0.20*0.068+ 0.03*0.31=0.2755

城市：郊区：农村=

0.5172:0.3673:0.2755：1.1600

求得充电桩在城市，郊区，农村中的比例分别为 44% 31% 25%

由以上分析可知影响计划的关键因素是地理分

Super charger 最佳规划求解

因为粒子群算法是采用解的集合的合作模式给出最优解的集合，因为需要的信息不用很多，对问题要求低，并且与遗传算法相比较更加容易实现，所以我们建议采用粒子群方法优化求解模型。由于模型篇幅有限制此处给出思维导图，此方法引用自论文

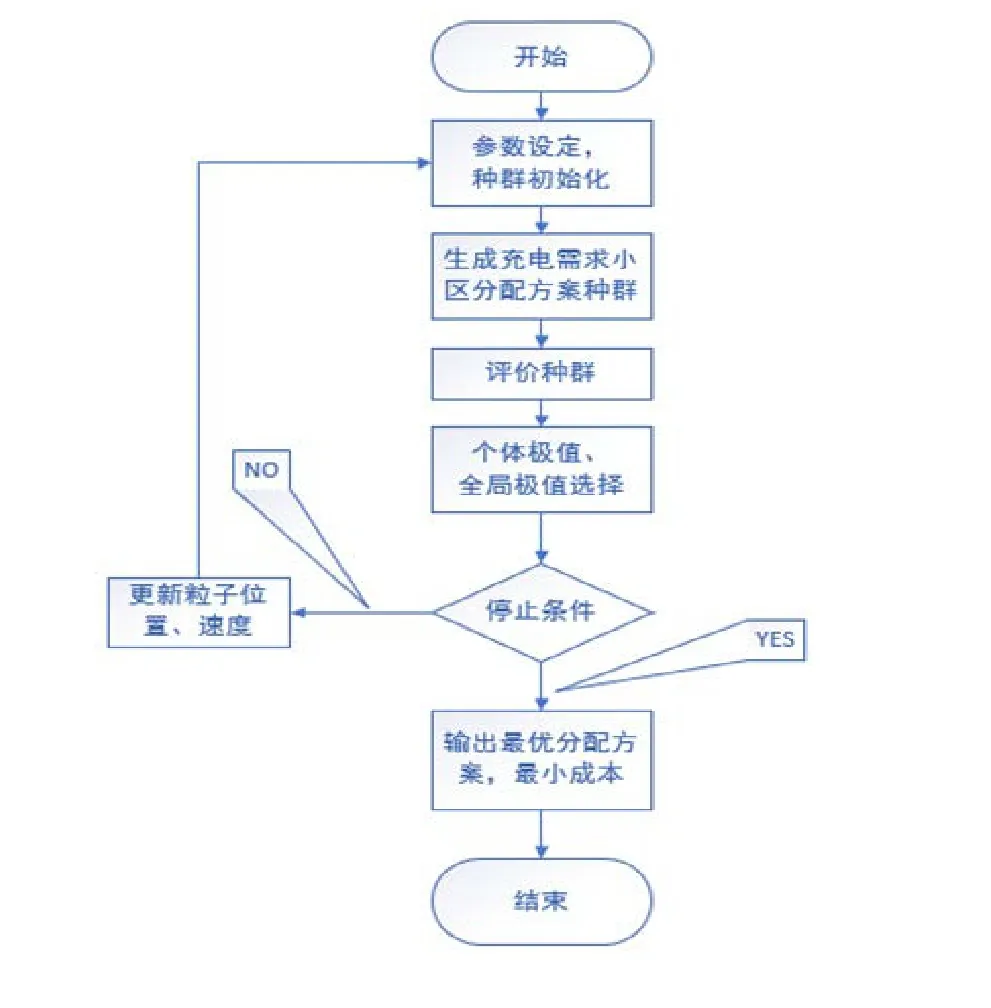
目的地式充电最佳求解

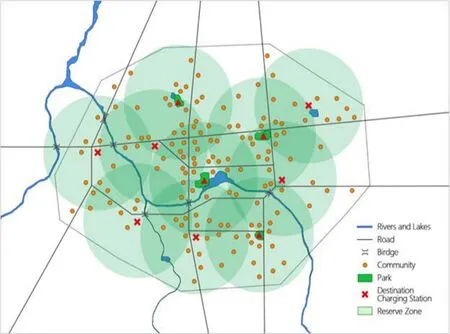
从图中看出避障效果良好，用户至簇中心的障碍距离都是绕过障碍的路径距离。仿真效果表明其算法是有效的。如果对于中心点建立目的地式电桩是有事迹意义的。

1.6.3.2 确定充电器安装的发展模型求解

查询资料可知

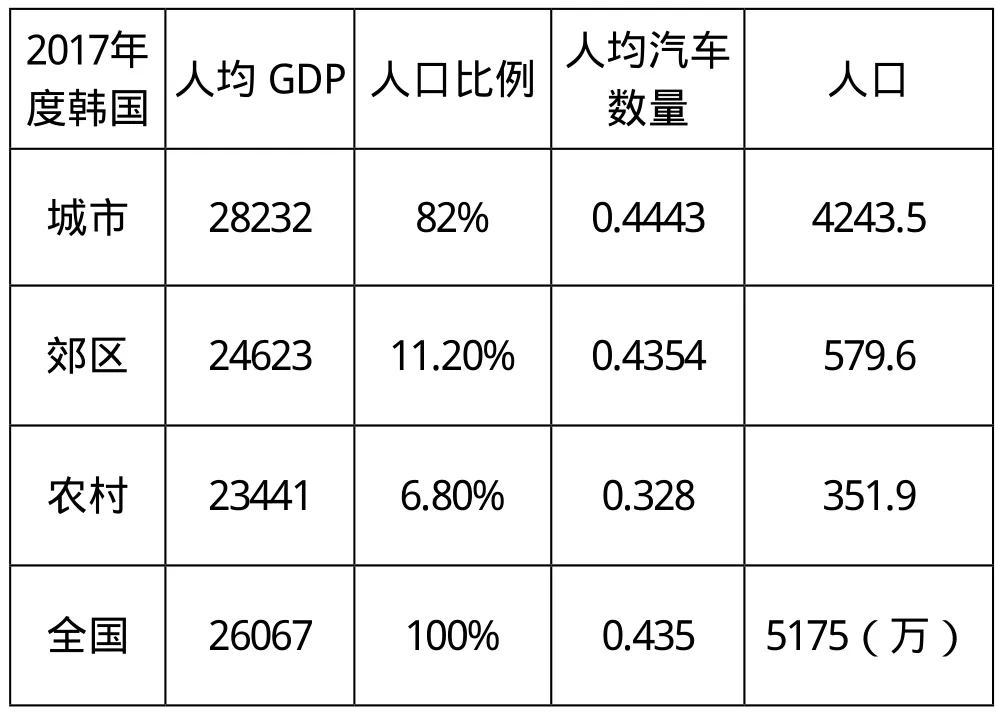
2017年度韩国 人均GDP人口比例 人均汽车数量 人口城市 28232 82% 0.4443 4243.5郊区 24623 11.20% 0.4354 579.6农村 23441 6.80% 0.328 351.9全国 26067 100% 0.435 5175（万）

对韩国的相关数据进行归一化处理得到新表

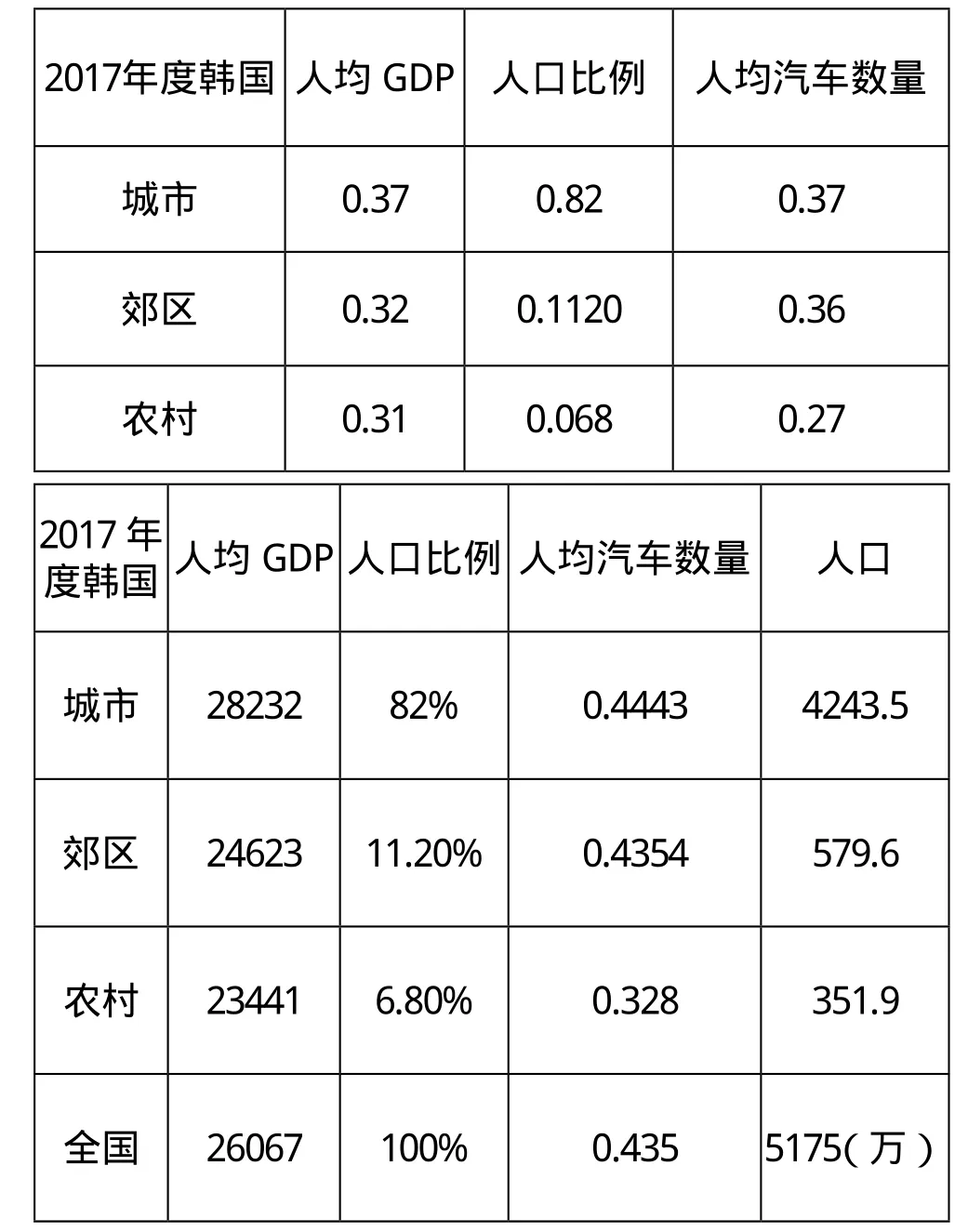
2017年度韩国 人均GDP 人口比例 人均汽车数量城市 0.37 0.82 0.37郊区 0.32 0.1120 0.36农村 0.31 0.068 0.27 2017年度韩国人均GDP人口比例 人均汽车数量 人口城市 28232 82% 0.4443 4243.5郊区 24623 11.20% 0.4354 579.6农村 23441 6.80% 0.328 351.9全国 26067 100% 0.435 5175（万）

城市 Z=0.62*0.37+0.14*0.82+0.24*0.37=0.4330

郊区 Z=0.62*0.32+0.14*0.1120+0.24*0.36=0.30 05

农村 Z=0.62*0.31+0.14*0.068+0.24*0.27=0.2665

结论：为了使得利益最大，应当先发展城市，再发展郊区，最后发展农村，符合客观的规律，因为发展城市往往能带来更大的经济效益，惠及更多的市民。

1.6.3.3 电动汽车全面发展时间表模型求解

通过matlab求解

得到电动车占比与时间的数据，如表

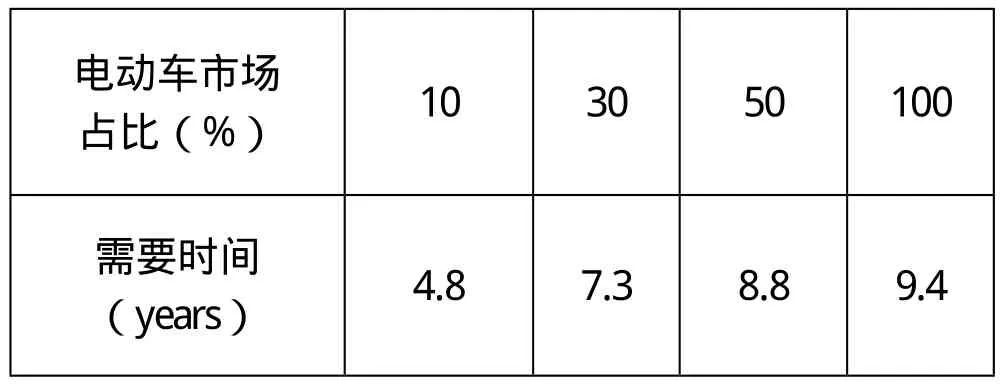
电动车市场占比（%） 10 30 50 100需要时间（years） 4.8 7.3 8.8 9.4

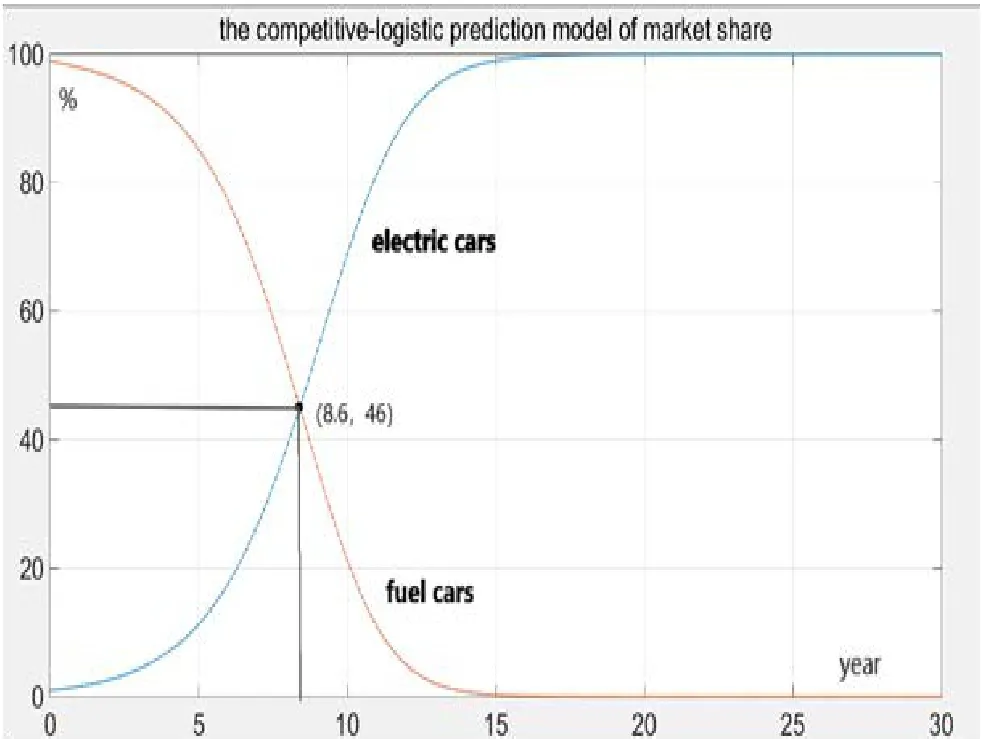
以及未来的电动汽车市场占比，燃油汽车市场占比图，建议政府在图中交点横坐标处为最迟禁止燃油车进入市场年份。如果在这之前禁止，那么将使实际占比图的交点向前

移动，让全电动时代早日到达。

1.6.4 模型评价

1.6.4.1 南韩电桩的最佳数量及分配和规划模型评价

本模型首先通过美国和南韩的情况找到共同影响因子，得到两者的电桩饱和量比例，以及分配比按照任务一的分配方式进行分配。它是任务一模型的修正引用，通过它确定了韩国充电桩的最佳数值和比例。其次使用目标规划-粒子群法和K-Medoids带障碍约束空间聚类分析方法对规划进行了求解并进行了解释它们的优点：

①在考虑电动汽车车主分布特性的基础上，根据单目标非线性规划方法，给出了充电站本之和达到最小的规划模型。对于它的求解用了比较受欢迎的启发式算法 -粒子群算法。此模型求解可得充电站的位置和其电容量。但此次建模型的不足在于没有进行数据对模型的检验，我们只是给了一个解决方案，还应把模型投于实践并根据实际进行改进。

②引用基于遗传和划分相结合的一个障碍约束空间聚类分析方法 {}，设计了一个 K-Medoids 带障碍约束空间聚类分析模型—固定式电桩布置由结果知它具有快速求解性和稳定性，对于目的地式电桩的规划是一种贴合实际的模型。

1.6.4.2 确定充电器安装的发展模型评价

本模型通过层次分析法，通过专家点评可以的到各影响因素科学的权重比，对于量化影响因子的设定做了一个优势补充，然后利用任务一模型的评价方法对未来发展规划给出了合理的解释，此模型可以进行多个国家的拓展。

1.6.4.3 电动汽车全面发展时间表模型评价

此模型类比生态圈种群竞争模型，得到电动汽车与燃油汽车竞争的 logstic阻滞增长模型，理论上诠释了竞争中此消彼长的模式，通过数据在MATLAB中求解画图，实践证明了理论。此模型适用于未来电车计划发展过程中不断的修正，预测参考。

[1]司守奎 孙兆亮.数学建模算法与应用[M].2.国防工业出版社, 2016.

[2]姜启源 谢金星 叶俊.数学模型[M].3.高等教育出版社, 2003.

[3]刘飞.北京电动汽车充电站布局规划研究[D].北京物资学院, 2015.

[4]曾鸣.基于智能电网的电动汽车充馈电调度策略研究[D].电子科技大学, 2016.

[5]乌云娜 李芳 徐传博 谢超 许儒航 .目的地充电的电动汽车分布式充电桩选型[J].河南科技大学学报(自然科学版）, 2018, 39(2).

[6]中汽协会网络部.2017年12月份美国轻型车(分制造商)销量[EB/OL].[2018-2-10]. http://www.caam.org.cn/america/20180123/1405214929.html .

[7]网易汽车.韩国新能源车2017年销量增41.6% 电动车销量破万[EB/OL].[2018-2-10].http://www.evpartner.com/news/7/detail-33501.html .

[8]网易汽车.人均拥有0.766辆汽车 美国汽车拥有量增长创新高[EB/OL].[2018-2-10].http://auto.163.com/18/0125/07/D8VRECD1000884MM.html .

[9]环球网综合报道.悉尼经济增长为全澳最佳贡献全国三成GDP增幅[EB/OL].[2018-2-10].http://world.huanqiu.com/exclusive/2016-02/8549088.html .

[10]新华网 .悉尼经济增韩国汽车保有量接近1600万同期增长3.2%[EB/OL].[2018-2-10].http://inf.315che.com/n/2007_01/29650/ .