等腰梯形蜂窝芯玻璃钢夹芯板的面外压缩性能

郑吉良，彭明军，孙 勇

(昆明理工大学 材料科学与工程学院，昆明 650093)

等腰梯形蜂窝芯玻璃钢夹芯板的面外压缩性能

郑吉良，彭明军，孙 勇

(昆明理工大学 材料科学与工程学院，昆明 650093)

利用材料试验机对玻璃钢(FRP)夹芯板面外压缩性能进行实验测试与模拟研究。结果表明：夹芯板面外压缩变形可分为弹性变形与断裂两个阶段。蜂窝芯中part 2胞壁厚度t1与part 2高度h比值t1/h较大时，夹芯板以屈服方式变形；t1/h较小时，夹芯板以屈曲方式变形。蜂窝芯中part 2为夹芯板主要承载构件，蜂窝芯中part 1与part 3对part 2起到固支作用，面板对蜂窝芯起到固支作用。蜂窝芯中part 2胞壁厚度为夹芯板面外压缩抗压强度影响的主要因素，蜂窝芯胞壁边长影响次之，而蜂窝芯中part 1，part 3与面板厚度的影响较小。夹芯板总高度一定时，随着蜂窝芯层数增加，夹芯板抗压强度逐渐增大。

等腰梯形蜂窝芯；玻璃钢夹芯板；应力-应变曲线；抗压强度；屈曲变形；屈服变形

蜂窝夹芯复合板由上、下面板与中间厚而质轻的夹芯构成，是一种轻质高效结构功能材料。由于它具有较高的比强度、比刚度和较好隔热、减振与耐冲击等优点而在航空、航海与高速列车等领域得到广泛的应用[1,2]。由于蜂窝夹芯复合板主要承受弯曲和冲击载荷等，因而其面外压缩性能具有决定性作用。国内外大量文献对蜂窝夹芯复合板面外压缩性能进行了详细研究。周祝林等[3]对玻璃钢蜂窝夹芯板的面外压缩弹性模量和抗压强度等进行了详细研究。孙亚平等[4,5]建立了以原纸环压强度为控制的纸蜂窝结构面外载荷理论模型和临界载荷计算方法，并与实验结果作了对比。程小全等[6]采用准静态横向压缩方法对Nomex蜂窝夹芯板的面外压缩性能及弯曲性能进行了实验研究。王中钢等[7]模拟研究加强筋结构参数对正六角铝蜂窝屈曲失稳影响。Wadley等[8]利用模压成型方法制备了四面体桁架夹芯结构的304不锈钢三明治板，并对这种三明治板的比强度和比刚度进行研究。Paik等[9]通过实验研究夹芯板面外压缩性能，给出铝蜂窝压缩强度与变形量关系。Cote等[10]利用钎焊方法制备不锈钢方孔蜂窝，并对其面外压缩性能进行详细研究，并与现有六边形铝蜂窝结构性能作比较。Meraghni等[11]利用有限元法、等效刚度法与实验相结合，对不规则六角形聚丙烯蜂窝芯进行模拟和实验研究。

本工作使用的等腰梯形玻璃钢蜂窝芯为新型π类蜂窝芯，应用真空保压压力成型方法制作玻璃钢蜂窝芯，所得蜂窝芯为整体结构，省略传统蜂窝芯黏结步骤，避免个别蜂窝芯胞壁之间漏黏结缺陷。在有限元软件ANSYS结构静力分析模块中，建立等腰梯形蜂窝芯玻璃钢夹芯板面外压缩有限元模型，对其破坏机理进行分析，并讨论夹芯板结构参数包括蜂窝芯胞壁厚度、胞壁边长、蜂窝芯高度以及面板厚度对其面外压缩强度的影响；同时研究夹芯板总高度一定工况下，蜂窝芯层数对其面外压缩抗压强度的影响。

1 试样平压实验

在测试等腰梯形蜂窝芯玻璃钢夹芯板面外压缩性能时，参照GB/T 1453-2005《夹层结构或芯子平压性能试验方法》和ASTM C365/C365M-16标准。由昆明理工大学蜂潮科技有限公司应用真空保压压力成型的方法，制成单向玻璃纤维排布方向不同的等腰梯形玻璃钢蜂窝芯；应用真空灌注法制备单向玻璃纤维质量分数约70%的玻璃钢面板。蜂窝芯与面板之间用胶黏剂黏结成夹芯板结构。利用万能材料试验机(INSTRON 8832)进行夹芯板面外压缩实验，获得试件应力-应变曲线。试件破坏方式为蜂窝芯上下端部被压溃。

2 试件面外压缩破坏方式有限元分析

2.1 有限元模型

根据试件实验规定要求，在有限元软件ANSYS结构静力分析模块中，建立等腰梯形蜂窝芯玻璃钢夹芯板沿着图1(a)中z方向面外压缩有限元模型。等腰梯形蜂窝芯玻璃钢夹芯板结构与蜂窝芯单元胞体模型及结构参数，如图1所示。

图1 等腰梯形蜂窝芯玻璃钢夹芯板结构(a)与蜂窝芯单元胞体模型及结构参数(b)Fig.1 FRP sandwich panel with isosceles-trapezoid honeycomb core geometry (a) and the model and structure parameters of unit cell in honeycomb core (b)

由于等腰梯形蜂窝芯中单向玻璃纤维排布方向具有差异性，part 1与part 3中单向玻璃纤维排布方向与图1(a)中y轴方向平行，part 2中单向玻璃纤维排布方向与图1(a)中z轴方向平行。有限元结构静力学分析时，给定part 1, part 3与part 2本体材料参数不同；因此，需要在有限元建模时，将等腰梯形玻璃钢蜂窝芯分成3部分，分别为part 1, part 2与part 3。面板中单向玻璃纤维排布方向与图1(a)中y轴方向平行。面板本体材料参数[12]给定弹性模量Ey=63.43GPa,Ex=Ez=8.73GPa,泊松比νxy=νyz=0.263,νxz=0.086, 剪切模量Gxy=Gyz=5.14GPa,Gxz=4.02GPa; 蜂窝芯中part 1与part 3本体材料参数给定弹性模量Ey=63.43GPa,Ex=Ez=8.73GPa, 泊松比νxy=νyz=0.263,νxz=0.086, 剪切模量Gxy=Gyz=5.14GPa,Gxz=4.02GPa; 蜂窝芯中part 2本体材料参数给定弹性模量Ez=63.43GPa,Ex=Ey=8.73GPa, 泊松比νxz=νyz=0.263,νxy=0.086,剪切模量Gxz=Gyz=5.14GPa,Gxy=4.02GPa。面板的厚度为1mm，蜂窝芯中part 1, part 2与part 3的胞壁厚度为1mm。通过对计算精度与效率的权衡，取图2(a)中有限元模型进行边界条件设置。上面板的上表面给定图1(a)中z轴方向位移，下面板下表面给定固定约束。有限元模型、蜂窝芯胞体结构参数与边界条件，如图2所示。

图2 等腰梯形玻璃钢蜂窝芯夹芯板沿z轴方向面外压缩有限元模型(a)、蜂窝芯胞体结构参数(b)与有限元模型边界条件(c)Fig.2 Out-plane compressive finite element model along the z-axis for the FRP sandwich panel with isosceles-trapezoid honeycomb core (a) and the structure parameters of unit cell in honeycomb core (b) and the boundary conditions of finite element model (c)

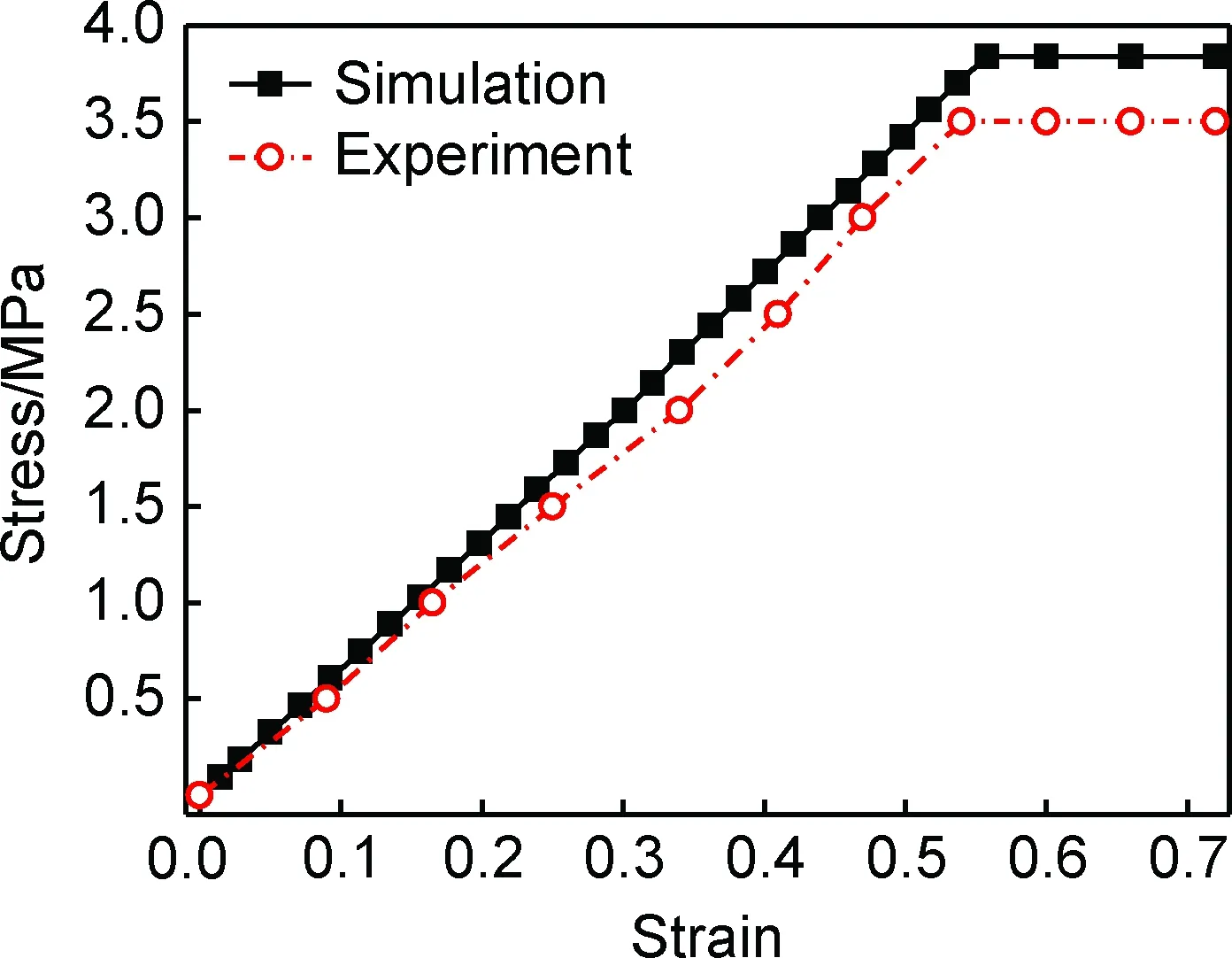
图3 实验与有限元计算获得试件应力-应变曲线对比Fig.3 Experimental stress-strain curves of sample compared with the FE-prediction

2.2 试件面外压缩破坏机理分析

实验与有限元计算获得试件应力-应变曲线进行对比，如图3所示。夹芯板被下压0.03, 0.67mm与1.37mm时刻，其等效应力的分布云图,如图4所示。

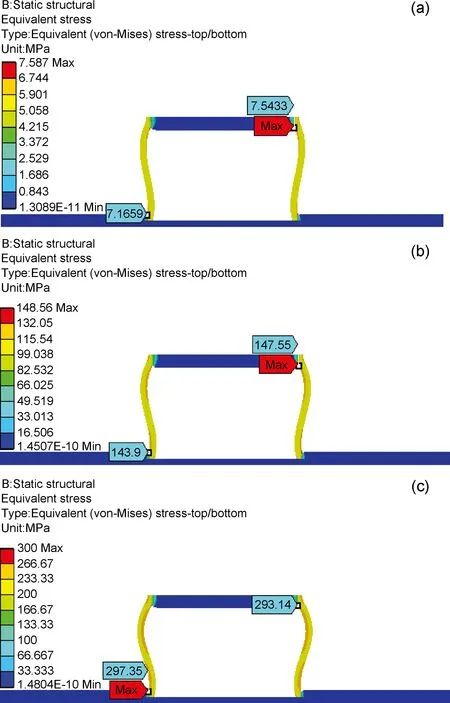
图4 面外压缩位移对等腰梯形蜂窝芯玻璃钢夹芯板等效应力云图影响(a)0.03mm;(b)0.67mm;(c)1.37mmFig.4 Effects of out-plane compressive displacement on the equivalent stress cloud pictures of FRP sandwich panel with isosceles-trapezoid honeycomb core(a)0.03mm;(b)0.67mm;(c)1.37mm

根据图3中应力-应变曲线可知：等腰梯形蜂窝芯玻璃钢夹芯板面外压缩变形大致分为两个阶段，即弹性变形和压溃断裂。根据图4中面外压缩等腰梯形蜂窝芯玻璃钢夹芯板的等效应力云图可知：随着面外压缩位移增加，最大等效应力出现在蜂窝芯中part 2与part 1, part 3交接位置处，因此试件破坏位置出现在part 2与part 1, part 3交接位置，这与实验过程中蜂窝芯上下端部被压溃现象吻合，说明有限元模型的准确性。

2.3 part 1, part 2, part 3与面板材料本体参数对夹芯板面外压缩强度的影响

蜂窝芯中part 1, part 2与part 3中单向玻璃纤维排布方向对等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度影响，如图5所示。面板中单向玻璃纤维排布方向对等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度影响，如图6所示。

图5 蜂窝芯中part 1, part 2与part 3中单向玻璃纤维排布方向对等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度影响Fig.5 Effects of glass fiber arrangement with the single axis of part 1, part 2 and part 3 in honeycomb core on out-plane compressive strength of FRP sandwich panel with isosceles-trapezoid honeycomb core

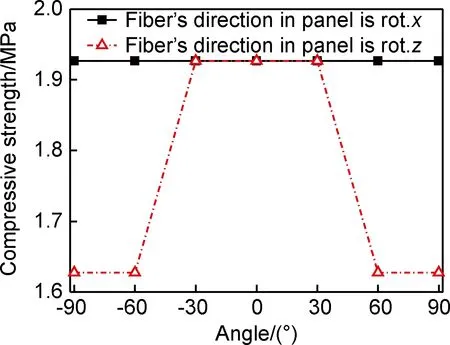
图6 面板中单向玻璃纤维排布方向对等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度影响Fig.6 Effects of glass fiber arrangement with the single axis in face sheet on out-plane compressive strength of FRP sandwich panel with isosceles-trapezoid honeycomb core

根据图5的part 2中单向玻璃纤维的排布方向绕图1(a)中x轴旋转与part 1, part 3中单向玻璃纤维排布方向绕图1(a)中x轴旋转对等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度影响对比曲线可知：蜂窝芯中part 2为夹芯板面外压缩主要承载构件。根据图5的part 2中单向玻璃纤维排布的方向绕图1(a)中y轴旋转与part 1, part 3中单向玻璃纤维排布的方向绕图1(a)中z轴旋转对等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度影响对比曲线可知：同样能够得到蜂窝芯中part 2为夹芯板面外压缩主要承载构件的结论，同时也可看出part 1, part 3在蜂窝芯中起

到固支part 2作用，增强夹芯板面外压缩抗压强度。根据图6的面板中单向玻璃纤维排布方向绕图1(a)中x轴与z轴旋转对等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度的影响曲线可知：面板对蜂窝芯起到固支的作用，同时为尽可能提高夹芯板面外压缩抗压强度，应该保持面板中单向玻璃纤维排布的方向与蜂窝芯中part 1, part 3中单向玻璃纤维排布方向一致。同时根据图5的part 1, part 3中单向玻璃纤维排布的方向绕图1(a)中x轴旋转与图6的面板中单向玻璃纤维排布方向绕图1(a)中x轴旋转对等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度影响对比曲线可知：蜂窝芯中part 1, part 3与面板中单向玻璃纤维排布方向对夹芯板面外压缩抗压强度影响微弱，因此为简化计算模型复杂程度，可以对夹芯板的整体给定part 2材料参数。综合图5与图6分析可得，蜂窝芯中part 1, part 3对part 2起到固支作用，面板对蜂窝芯起到固支作用； 蜂窝芯中part 2为夹芯板面外压缩主要承载构件。

3 蜂窝芯胞体与面板结构参数对试件面外压缩抗压强度影响

图7(a)，(b),(c)分别为蜂窝芯中part 2胞壁厚度t1，蜂窝芯中part 1, part 3胞壁厚度t2以及面板厚度对等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度的影响。

由图7(a)可知：随着蜂窝芯中part 2的胞壁厚度t1增加，等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度显著增大。其原因为蜂窝芯中part 2是夹芯板面外压缩主要承载构件，随着t1增加，增大了蜂窝芯中part 2承载面积；因此，随着t1增加，夹芯板面外压缩抗压强度显著增大。由图7(b)可知：随着蜂窝芯中part 1, part 3胞壁厚度t2增加，等腰梯形蜂窝芯玻璃

钢夹芯板面外压缩抗压强度先逐渐增大，后又逐渐降低。其原因为蜂窝芯中part 1, part 3对part 2起到固支作用，随着t2增加，part 1, part 3对part 2固支作用逐渐加强；因此夹芯板面外压缩抗压强度随着t2增加而先增大；之后随着t2继续增加，虽然蜂窝芯中part 1, part 3对part 2固支作用加强，但也加强part 1, part 3与part 2交接位置缺陷性；因此，随着t2继续增大，又出现夹芯板面外压缩抗压强度降低的现象。由图7(c)可知：蜂窝芯中part 1, part 2与part 3胞壁厚度t1,t2为1mm时，随着面板厚度增加，等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度先缓慢增大，后又逐渐降低。其原因为面板对蜂窝芯起到固支作用，随着面板厚度增加，面板对蜂窝芯固支作用加强；因此夹芯板面外压缩抗压强度随着面板厚度增加先缓慢增大；之后随着面板厚度继续增加，虽然面板对蜂窝芯固支加强，但也加强蜂窝芯中part 1, part 3与part 2交接位置缺陷性；因此，随着面板厚度继续增大，又出现夹芯板面外压缩抗压强度降低现象。同时t1,t2与面板厚度分别由1mm增大到5mm时，等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度数值差额分别为6.93,0.28,0.16MPa，同样可以得到蜂窝芯中part 2为夹芯板面外压缩主要承载构件，蜂窝芯中part 1, part 3对part 2起到固支作用，面板对蜂窝芯起到固支作用的结论。综合分析图7(a), (b), (c)曲线可知：实际工程应用中，应尽量增加t1而降低面板厚度，以获得高面外压缩抗压强度夹芯板。

图8(a)，(b),(c),(d)分别为蜂窝芯中单元胞体边长，蜂窝芯的高度h，蜂窝芯脱模斜度α以及蜂窝芯倒角半径R对等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度的影响。

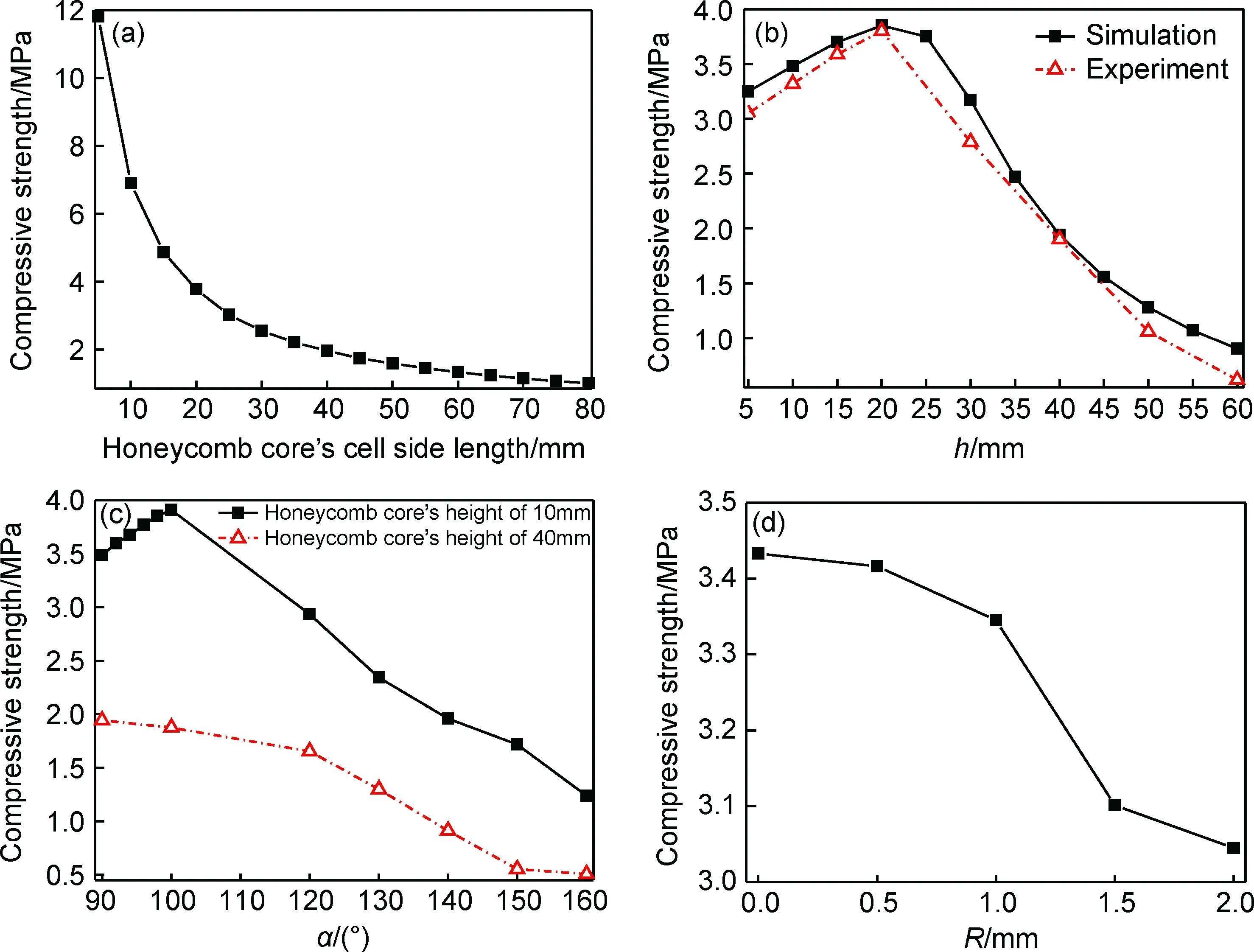
图8 等腰梯形蜂窝芯玻璃钢夹芯板结构参数对其面外压缩抗压强度影响 (a)蜂窝芯中单元胞体边长;(b)h;(c)α;(d)RFig.8 Effects of structure parameters of FRP sandwich panel with isosceles-trapezoid honeycomb core on its out-plane compressive strength (a)the unit cell side length in honeycomb;(b)h;(c)α;(d)R

由图8(a)可见，等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度随蜂窝芯胞壁边长增加而呈负指数规律变化。当蜂窝芯胞壁边长增大到一定值时，夹芯板面外压缩抗压强度下降趋势变得平缓。由此可以得出，在设计夹芯板结构时，夹芯板面外压缩抗压强度允许情况下，应尽量增加蜂窝芯胞壁边长，这样可大幅度减轻夹芯板质量。

由图8(b)可见，随着蜂窝芯的高度h增加，等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度先逐渐增大，后又逐渐降低。当蜂窝芯中part 2胞壁厚度t1与part 2高度h比值t1/h较大时，即t1较大而h较小，part 2胞壁在面外压缩载荷作用下，不易发生屈曲变形，而是以屈服方式变形，亦即试样变形更接近于实体材料变形，故其夹芯板面外压缩抗压强度可按公式(1)[13]进行计算：

(1)

式中：σs为单向玻璃纤维排布的玻璃钢面板断裂强度值；a为蜂窝芯边长的平均值；h为蜂窝芯的高度。相反，当蜂窝芯中part 2胞壁厚度t1与part 2高度h比值t1/h较小时，即t1较小而h较大，part 2胞壁在面外压缩载荷作用下，易于先以屈曲方式变形，而不以屈服方式变形，亦即试样变形更接近于薄壁结构变形，故其夹芯板面外压缩抗压强度可按公式(2)[13]进行计算：

(2)

式中：E0为单向玻璃纤维排布的玻璃钢面板等效弹性模量；ν为单向玻璃纤维排布的玻璃钢面板等效泊松比;因此，夹芯板面外压缩抗压强度随h增加而先逐渐增大，后又逐渐降低。

实际工程应用中，为降低等腰梯形玻璃钢蜂窝芯成型难度，模具设计中通常给定蜂窝芯脱模斜度，即图2(b)中part 1, part 3与part 2夹角α，降低蜂窝芯脱模难度。同时模具设计中也要给定蜂窝芯倒角，即图2(b)中part 1, part 3与part 2接触位置倒角半径R，以降低蜂窝芯成型难度与脱模难度。

由图8(c)可见，蜂窝芯高度为10mm时，等腰梯形蜂窝芯玻璃钢夹芯板面外压缩以屈服变形方式为主；当α较小时，夹芯板仍以屈服方式进行变形，夹芯板面外压缩抗压强度按公式(1)进行计算；当α较大时，夹芯板以屈曲方式进行变形，夹芯板面外压缩抗压强度按公式(2)进行计算；因此，等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度随着蜂窝芯脱模斜度α增大，呈先增大后降低趋势；蜂窝芯高度为40mm时，等腰梯形蜂窝芯玻璃钢夹芯板面外压缩以屈曲变形为主；随着α增大，夹芯板稳定性降低；因此，等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度随着蜂窝芯脱模斜度α增大，呈逐渐降低趋势。综合分析图8(c)可知，α对π型蜂窝芯夹芯板面外压缩变形方式具有重要影响。由图8(d)可见，等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度随着蜂窝芯倒角半径R增大，呈逐渐降低趋势。其原因为随R增加，增大了蜂窝芯中part 1, part 3与part 2交接位置承载横向切应力绝对值，促使交接位置更容易被压溃；因此，随着R增大，夹芯板面外压缩抗压强度逐渐降低。综合分析图8(c), (d)可知，实际工程应用中，应该适当增大蜂窝芯脱模斜度α，降低蜂窝芯倒角半径R，以满足π型蜂窝芯夹芯板面外压缩抗压强度，从而降低蜂窝芯脱模难度与成型难度。

4 多层蜂窝芯夹芯板面外压缩有限元分析

在ANSYS有限元软件结构静力学模块中，建立单层、双层与三层等腰梯形蜂窝芯玻璃钢夹芯板面外压缩有限元模型，如图9所示。图9中等腰梯形蜂窝芯玻璃钢夹芯板总高度为22mm，单层蜂窝芯中蜂窝芯高度为20mm，双层蜂窝芯中每层蜂窝芯高度为9.5mm，三层蜂窝芯中每层蜂窝芯高度为6mm。面板厚度为1mm，蜂窝芯中胞体厚度为1mm。上面板上表面给定图1(a)中z轴方向2mm向下位移，下面板下表面给定固定约束，有限元模型本体材料参数参照2.1节。

图9 单层与多层等腰梯形蜂窝芯玻璃钢夹芯板面外压缩有限元模型 (a)单层;(b)双层;(c)三层Fig.9 Out-plane compressive finite element model for FRP sandwich panel with single-layer or multi-layers isosceles-trapezoid honeycomb core (a)single-layer;(b)two-layers;(c)three-layers

图10为面外压缩的单层与多层等腰梯形蜂窝芯玻璃钢夹芯板中单个胞体面外与面内等效应力分布云图。图11(a), (b)分别为面外压缩的单层与多层等腰梯形蜂窝芯玻璃钢夹芯板中单个胞体面外与面内等效应力分布曲线。

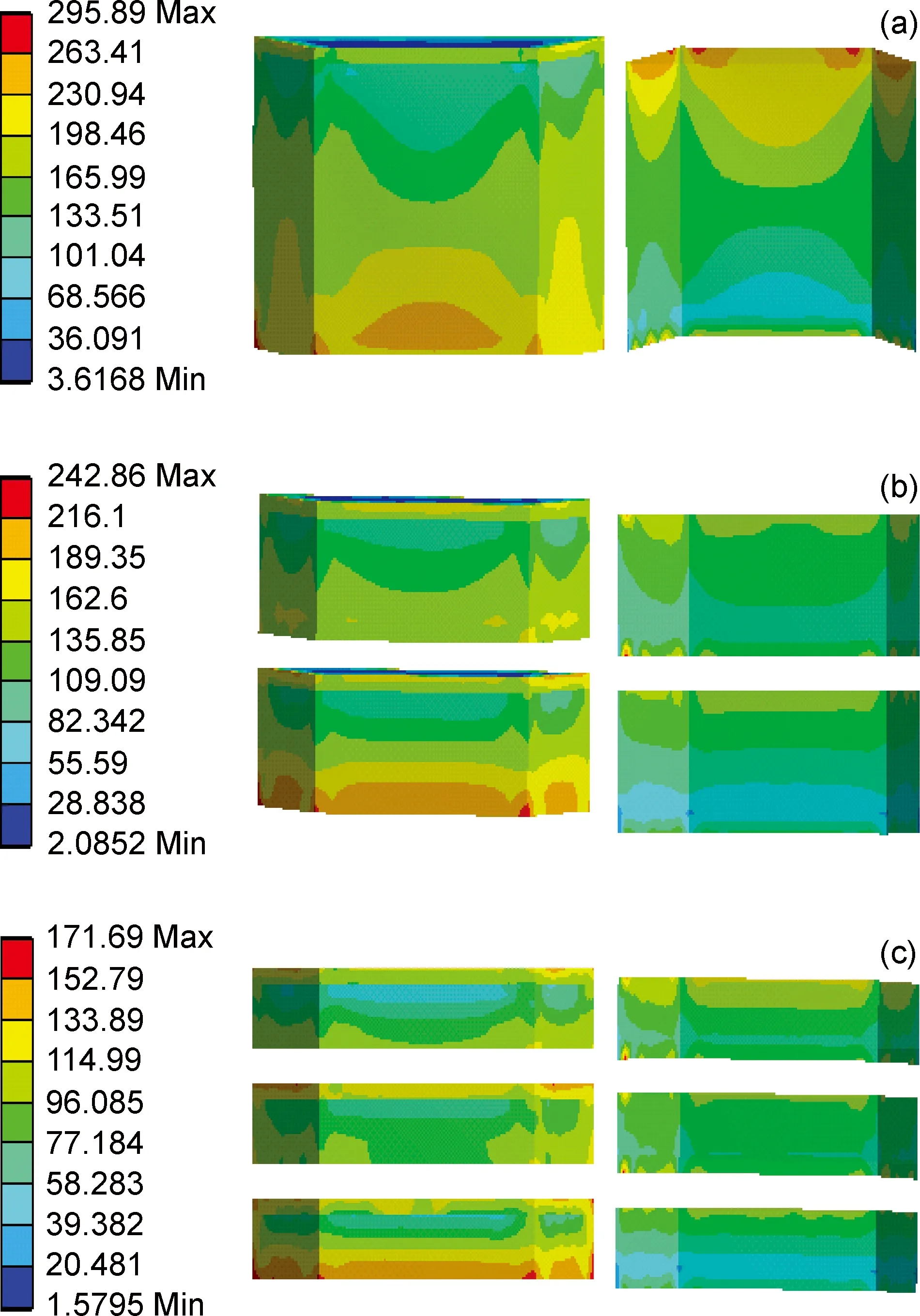
图10 面外压缩的单层与多层蜂窝芯玻璃钢夹芯板中单个胞体面外与面内等效应力分布云图 (a)单层;(b)双层;(c)三层Fig.10 Outside and inside equivalent stress cloud pictures of unit cell in out-plane compressive FRP sandwich panel with single-layer or multi-layers isosceles-trapezoid honeycomb core (a)single-layer; (b)two-layers;(c)three-layers

由图10, 11(a),(b)可见，等腰梯形蜂窝芯玻璃钢夹芯板总高度一定工况下，随着蜂窝芯层数增加，夹芯板等效应力逐渐降低，即夹芯板面外压缩抗压强度逐渐增大。结合本工作在文献[14]中对夹芯板传热学分析可知：单纯增加蜂窝芯高度，对夹芯板当量导热率不利；如果单纯降低夹芯板当量导热率，而忽略夹芯板面外压缩抗压强度，应该考虑更换夹芯层材料，例如使用泡沫材料； 如果夹芯板同时满足于面外压缩抗压强度

与隔热性能要求，多层蜂窝芯夹芯板将是很好的选择。且由图11(a), (b)可见，蜂窝芯中part 1, part 3与面板位置的等效应力出现较小平缓曲线，而蜂窝芯中part 2位置的等效应力相对较高，这再次说明了蜂窝芯中part 1, part 3对part 2起到固支作用，而面板对蜂窝芯起到固支作用，蜂窝芯中part 2为等腰梯形蜂窝芯玻璃钢夹芯板面外压缩主要承载构件。

5 结论

(1)等腰梯形蜂窝芯玻璃钢夹芯板面外压缩过程中，夹芯板面外压缩变形可分为两个阶段，即弹性变形与断裂阶段。

(2)蜂窝芯中part 2为等腰梯形蜂窝芯玻璃钢夹芯板面外压缩主要承载构件，蜂窝芯中part 1与part 3对part 2起到固支作用，面板对蜂窝芯起到固支作用。

(3)蜂窝芯中part 2胞壁厚度t1与part 2高度h比值t1/h较大时，等腰梯形蜂窝芯玻璃钢夹芯板面外压缩以屈服变形方式进行；而t1/h较小时，以屈曲变形方式进行。

(4)实际工程应用中，应该适当增大蜂窝芯脱模斜度，降低蜂窝芯倒角半径，以满足等腰梯形蜂窝芯玻璃钢夹芯板面外压缩抗压强度，从而降低蜂窝芯脱模难度与成型难度。

(5)多层蜂窝芯夹芯板同时满足于面外压缩抗压强度与隔热性能要求。

图11 面外压缩单层与多层等腰梯形蜂窝芯玻璃钢夹芯板中单个胞体面外与面内等效应力分布曲线 (a)面外;(b)面内Fig.11 Equivalent stress curves of unit cell in out-plane compressive FRP sandwich panel with the single-layer or multi-layers honeycomb core (a)outside;(b)inside

[1] 石晓朋, 李曙林, 常飞, 等. Nomex蜂窝复合材料冲击损伤及剩余压缩强度试验[J]. 航空材料学报, 2013, 33(6): 70-75.

SHI X P, LI S L, CHANG F, et al. Impact damage and post-impact compressive strength experiment of Nomex honeycomb sandwich panel[J]. Journal of Aeronautical Materials, 2013, 33(6): 70-75.

[2] 陈勇军, 左孝青, 史庆南, 等. 金属蜂窝的开发、发展及应用[J]. 材料导报, 2003, 17(12): 32-35.

CHEN Y J, ZUO X Q, SHI Q N, et al. Development and application of honeycombed metal[J]. Materials Review, 2003, 17(12): 32-35.

[3] 周祝林, 王亚熊. 夹层结构或芯子平压实验方法分析[J]. 玻璃钢, 2004, (1): 5-13.

ZHOU Z L, WANG Y X. Test method for flatwise compression properties of sandwich constructions or cores[J]. Fiber Reinforced Plastics, 2004, (1): 5-13.

[4] 孙亚平, 卢立新, 蔡和平. 纸蜂窝结构平压性能的实验研究[J]. 包装工程, 2013, 24(1): 14-15.

SUN Y P, LU L X, CAI H P. A study to the strength to the paper honeycomb core under axial compression[J]. Packaging Engineering, 2013, 24(1): 14-15.

[5] 孙亚平, 卢立新. 纸蜂窝结构参数对面外承载能力的影响[J]. 江南大学学报(自然科学版), 2004, 3(1): 52-55.

SUN Y P, LU L X. Effects of the structure parameters on the out-plane load of paper honeycomb[J]. Journal of Southern Yangtze University (Natural Science Edition), 2004, 3(1): 52-55.

[6] 程小全, 寇长河, 郦正能. 复合材料夹芯板低速冲击后弯曲及横向静压特性[J]. 复合材料学报, 2000, 17(2): 114-118.

CHENG X Q, KOU C H, LI Z N. Behavior of bending after low velocity impact and quasi-static transverse indentation of composite honeycomb core sandwich panels[J]. Acta Materiae Compositae Sinica, 2000, 17(2): 114-118.

[7] 王中钢, 姚松. 加筋正六角铝蜂窝异面力学特性与筋胞厚度匹配优化[J]. 航空材料学报, 2013, 33(3): 86-91.

WANG Z G, YAO S. Out-of-plane mechanical properties and thickness matching optimization between rib and cell thin-wall of reinforced regular hexagon aluminum honeycomb[J]. Journal of Aeronautical Materials, 2013, 33(3): 86-91.

[8] WADLEY H N G, FLECK N A, EVANS A G. Fabrication and structural performance of periodic cellular metal sandwich structures[J]. Composite Science and Technology, 2003, 63(16): 2331-2343.

[9] PAIK J K, THAYAMBALLI A K, KIM G S. The strength characteristics of aluminum honeycomb sandwich panels[J]. Thin-Walled Structures, 1999, 35(3): 205-231.

[10] COTE F，DESHPANDE V S，FLECK N A，et al. The out-of-plane compressive behavior of metallic honeycombs[J]. Materials Science and Engineering: A, 2004, 380(1-2): 272-280.

[11] MERAGHNI F，DESRUMAUX F，BENZEGGAGH M L. Mechanical behavior of cellular core for structural sandwich panels[J]. Composites Part A: Applied Science and Manufacturing, 1999, 30(6): 767-779.

[12] 郑吉良, 孙勇, 彭明军. 基于纤维拔出理论的复合材料力学性能的研究[J]. 兵器材料科学与工程, 2014, 37(2): 16-21.

ZHENG J L, SUN Y, PENG M J. Mechanical properties of composite material based on fiber pull-out theory[J]. Ordance Material Science and Engineering, 2014, 37(2): 16-21.

[13] 井玉安, 韩静涛, 果世驹, 等. 普碳钢蜂窝夹芯板的面外压缩性能[J]. 北京科技大学学报, 2006, 29(12): 1234-1240.

JING Y A, HAN J T, GUO S J, et al. Out-of-plane compressive characteristics of brazing mild steel honeycomb structures[J]. Journal of University of Science and Technology Beijing, 2006, 29(12): 1234-1240.

[14] 郑吉良, 孙勇. 单层与多层蜂窝芯玻璃钢蜂窝板的热性能模拟[J]. 复合材料学报, 2014, 31(2): 505-511.

ZHENG J L, SUN Y. Simulation of thermal performance for single layer and multilayer of the FRP honeycomb panel[J]. Acta Materiae Compositae Sinica, 2014, 31(2): 505-511.

(本文责编：寇凤梅)

Out-plane Compressive Properties for Isosceles Trapezoid Honeycomb Core of FRP Sandwich Panel

ZHENG Ji-liang,PENG Ming-jun,SUN Yong

(Faculty of Material Science and Engineering,Kunming University of Science and Technology,Kunming 650093,China)

The experiment and simulation investigations on out-plane compressive characteristics of FRP sandwich panel were conducted. The results show that two deformation stages are elastic deformation and fracture stages in out-plane compressive deformation. The yielding mode deformation ast1/hwhich is very big，while the buckling mode deformation ast1/hwhich is very small. The part 2 in the honeycomb core is main bearing part for sandwich panel，and the part 2 is supported by the part 1 and part 3 in the honeycomb core，while the honeycomb core is supported by the panel. So，the cell wall thickness of part 2 has the most significant influence on the compressive strength，and the influence by the cell wall side length of honeycomb core is the secondary，while the influence by the cell wall thickness of part 1 and part 3 in honeycomb core and the thickness of panel is the weakest. When the honeycomb core height is fixed，the compressive strength of FRP sandwich panel gradually increases along with honeycomb core layers increase.

isosceles-trapezoid honeycomb core;FRP sandwich panel;stress-strain curve;compressive strength;buckling deformation;yielding deformation

10.11868/j.issn.1001-4381.2014.001534

TB34

A

1001-4381(2017)02-0072-08

2014-12-22；

2016-07-10

彭明军(1982-)，男，博士，讲师，研究方向：复合材料结构力学性能，联系地址：云南省昆明市五华区莲华学府路30号昆明理工大学材料科学与工程学院(650093)，E-mail:18988294916@163.com