基于μ-σ积分变换的概率问题研究
马醒花,岳凤桐
(1.华北理工大学 理学院,河北 唐山 063210;2.唐山学院,河北 唐山 063000)
基于μ-σ积分变换的概率问题研究
马醒花1,岳凤桐2
(1.华北理工大学 理学院,河北 唐山 063210;2.唐山学院,河北 唐山 063000)
正态分布;概率密度;积分变换
在概率统计中一般正态分布化为标准正态分布的重要性不言而喻,而标准化的实质其实就是积分变换。本文重点阐述μ-σ积分变换在一维、二维正态分布问题研究中所起的作用,一方面揭示概率统计与高等数学联系密切,另一方面对正态分布这一重要的概念从积分变换的角度进行更加全面而深入的研究。
1 一维正态分布中的μ-σ积分变换
μ-σ积分变换在一维正态分布问题的研究中比较常见,通过变换可将一般正态分布标准化,从而使分布函数、概率密度简单化,一方面既便于理论上的研究,另一方面又可利用标准正态分布表求任一事件的概率值,且简单易行。
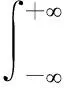
证明:
(1)
这是一般正态分布概率密度归一化性质的证明,利用μ-σ积分变换,可迎刃而解。
(2)已知X~N(μ,σ2),证明E(X)=μ
证明:
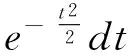
(2)
这是一般正态分布求数学期望,利用μ-σ积分变换及概率密度的性质即可证出。
(3)已知X~N(μ,σ2),证明D(X)=σ2

=σ2
(3)
此即一般正态分布求方差,利用μ-σ积分变换及分部积分法求得。
(4)已知X~N(μ,σ2),求E(X-μ)n

当n为偶数时
(4)
一般正态分布求n阶中心矩,求解时首先使用μ-σ积分变换,然后利用积分性质及伽玛函数的性质等推出结论。
(5)已知随机变量X~N(160,σ2),且P{120 解:因为P{120 已知P{120 这就是典型的正态分布经过μ-σ积分变换后,通过查表求事件的概率值的题目,此题如果不经过标准化,直接用概率密度去计算σ的值是不可能的或只能通过计算机算出近似值。 μ-σ积分变换在一维正态分布问题研究中引人注目,在二维正态分布问题研究中其作用更加突出,所做变换常常是双μ-σ积分变换,典型问题如下。 证明: 得 再做变量替换,令 得 (5) 本题使用了双μ-σ积分变换,其实质就是二重积分换元法。 解: (6) (7) (3)已知(X,Y)~N(μ1,σ12μ2,σ22ρ),求X,Y的协方差cov(X,Y)和相关系数ρXY 于是 即若X与Y不相关,则X与Y必独立,所以在正态分布的场合,独立与不相关是等价的。 基于μ-σ积分变换的概率问题系统介绍了μ-σ积分变换在一维及二维正态分布问题研究中的作用,说明高等数学与概率统计联系密切,同时也强化了一般正态分布标准化的重要性,即非标准化的随机变量只有通过标准化才能脱颖而出。 [1] 万星火.概率论与数理统计[M].北京:科学出版社,2007. [2] 盛骤,等.概率论与数理统计(第4版)[M].北京:高等教育出版社,2008. [3] 都超.正态分布k阶原点矩与方差的计算[J].考试周刊-数学教学与研究,2011,(27):65-66. [4] 马醒花.二重积分在单积分计算中的应用[J].高等数学研究,2017,(2):63-65. Research on Probability Problem Based on μ-σ Integral Transformation MA Xing-hua1,YUE Feng-tong2 (1.College of Science,North China University of Science and Technology,Tangshan Hebei 063210,China;2.Tangshan College,Tangshan Hebei 063000,China) normal distribution; probability density; integral transformation In probability statistics,it is self-evident that the importance of transformation from the general normal distribution into the standard normal distribution,and in fact the essence of standardization is integral transformation.The role of integral transformation in the study of one-dimensional and two-dimensional normal distribution was emphasized and discussed.On the one hand,the substantial connection between probability statistics and higher mathematics is revealed,and on the other hand,the important concept of normal distribution is comprehensively studied in-depth from the perspective of integral transformation. 2095-2716(2017)03-0105-04 2017-03-18 2017-05-10 华北理工大学教改项目(Z1613-13)。 O A2 二维正态分布中的 积分变换

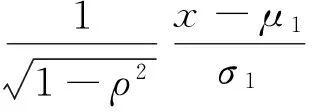
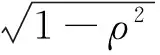



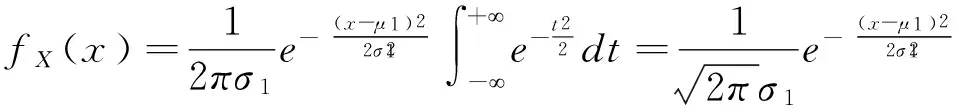
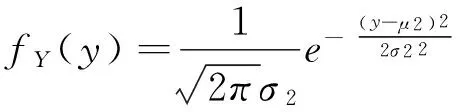




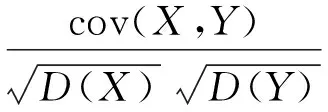
3 结论

