元胞自动机模型用于小区开放问题的分析
冯献磊,吴燕文,刘璇,王宏
(1.华北理工大学 电气工程学院,河北 唐山 063210;2.华北理工大学 理学院,河北 唐山 063210)
元胞自动机模型用于小区开放问题的分析
冯献磊1,吴燕文1,刘璇2,王宏2
(1.华北理工大学 电气工程学院,河北 唐山 063210;2.华北理工大学 理学院,河北 唐山 063210)
小区开放;道路通行能力;元胞自动机;交通流仿真
研究了开放小区对周边道路通行能力的影响。首先分析了影响道路通行能力的指标,然后运用元胞自动机模型对不同指标进行了随机仿真,使得其在单因子变量下达到最优解。结果表明:在小区面积为97.78 158.21 m2、形状为方形结构、周边道路为双向四车道,且道路交叉口红灯时间大约占整个循环周期的33.86%时,开放小区对周边道路车辆通行情况的缓解作用较为明显。
探究传统小区开放对周边道路通行能力[1]的影响,对我国最近出台的街区制推广、实践具有重要意义。关于小区开放对周边道路通行能力的影响,李向朋使用Braess悖论建立了区域微循环交通系统[2];袁绍欣等通过混杂Petri网模型对无信号交叉路口车流通行特性进行了分析描述[3];高海龙等利用TANNER公式得到无信号交叉路口车流临界间隙的计算值[4]。
该项研究运用元胞自动机交通流模型对该问题进行了仿真研究。首先确定了小区面积、小区基本形状、周边道路车流量分布和红绿灯时间间隔4个指标与吸纳密度之间的函数关系;其次通过仿真分别得到4个单一指标下的最优解;最后得到了4个指标最优解体系下,开放小区对车辆道路通行缓慢情况缓解作用较为明显。
1 小区开放问题的研究
1.1 开放小区的背景
2016年2月21日,国务院颁布的《中共中央关于进一步加强城市规划建设管理工作的若干意见》指出:“新建住宅要推广街区制,原则上不再建设封闭住宅小区。已建成的住宅小区和单位大院要逐步打开,实现内部道路公共化。”
建宅新政策引起了社会的广泛关注和讨论。一方面,街区制是对世界城市规划经验的总结,也是诸多发达国家通行的作法,如美国第五大道、英国牛津街和意大利蒙特拿破仑大街等。小区开放后,路网密度的提高、道路面积的增加和通行能力的提升可避免封闭小区和单位大院 “丁字路”、“断头路”等带来的交通堵塞;另一方面,住宅车流量增加、车速加快,不仅增加了交通安全隐患,还会导致周边路网的不确定性。
1.2 道路通行能力评价指标的选取
通过查阅相关资料,首先提出了选取评价指标的基本原则:高效性、安全性、稳健性、不相容性、目的性、代表性、实用性和易考核性。然后结合我国现在严峻的交通和城建住宅小区情况,如部分行驶车辆选择绕行较远的外环路段,也不穿行更近的市区干道;小区内部穿行会带来极大的安全隐患和噪音;进出小区交叉口的车辆增多会影响周边主路通行速度等。因此,车辆的行驶规则、小区开放原则是需要考虑的重点。基于上述分析,最后筛选出了 4 个评价指标:小区面积、小区基本形状、周边道路车流量分布和红绿灯时间间隔。
1.3 元胞自动机模型的建立
1.3.1相关概念
元胞自动机[5]是一个由具有离散、有限状态的元胞组成的元胞空间上按照一定的局部规则,在离散时间维上进行演化的动力学系统。最初是由冯·诺依曼在 20 世纪 50 年代发明。
元胞自动机的构建没有固定的数学公式,构成方式繁杂,变种多样且行为复杂,其作为一种动态模型,更多的是一种通用性的建模方法,在交通问题、社会学、生态学、计算机科学、物理学、化学等诸多领域都有广泛应用。
1.3.2 定义状态集
根据实际问题定义元胞自动机的状态集S(s1,s2,s3)(s1=0,s2=1,s3=-888),空白车道为s1,被小车占据的车道为s2,不可入区域为s3。
1.3.3 生成住宅小区附近轨道
根据小区附近的道路情况建立车道矩阵为L(R+ 2),车道长度为L,道路的车道数为R,车道矩阵可通过数学矩阵来模拟现实道路:

为了便于观察,利用 MATLAB 软件将车道矩阵可视化处理,得到如下车道,其中列向空白的位置为车道,第1列的空白位置为小区的出入口。
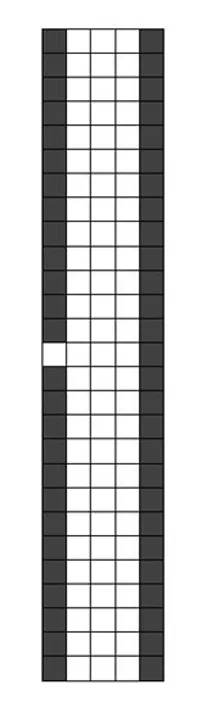
图1 MATLAB 随机仿真的部分可视化轨道
1.3.4利用傅里叶交通流随机为不同车道添加车辆
(1)傅里叶交通流[6]随机产生车辆数C。
(2)判断可添加车辆的车道数R,利用随机函数[7]将min (C,R) 随机添加到R条车道上。
1.3.5 基于以下前进换道规则[8]进行移动
(1)分为3段,分别从车辆前进方向的前、后位置来扫描每一辆车,依次是小区前面、小区和小区后面。
(2)对于小区前或后的车辆,如果该车前面的位置被其它行驶车辆车占据,则该车被标记为-2,表示换道准备;否则,该车以概率prob1前进到它前面的位置。
(3)当车的前面位置被其它行驶车辆占据时,则该车考虑换道,若这类车辆在前进规则中状态已经被标记为-2,则该车辆以概率prob2进行换道。
(4)优先考虑右向换道。

图2 车辆的前进换道示意图
1.3.6 引入车辆通过小区的概率q
由小区内、外部的交通网络及交通设施情况来确定车辆的通过概率q,即:与小区出入口紧挨的车道有q的概率的行驶车辆选择从小区穿行。通过小区的示意图如图3所示。
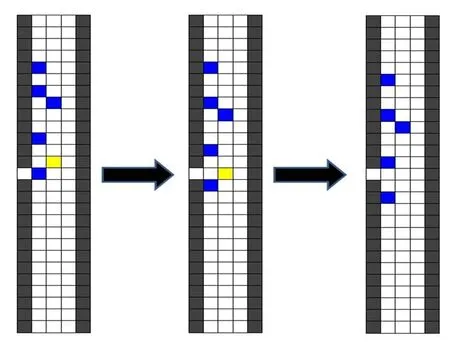
图3 车辆通过小区的右换道
周边干道的道路数为k,理论上的车辆吸纳数为L,单位长度的单车道拥有的机动车辆数为d,一般单向单车道中需穿行小区的车辆数与该车道车辆总数的比值为θ0,开放小区的可达度为c,车辆吸纳密度与可达度之间的转换系数为R,车辆通过小区的概率为q,即:整个道路域的吸纳车辆数与该内道所有车辆数的比值。
可达度是指周边道路上单位车辆经穿行小区满足缩短到达目的地时间的车辆所占比值。
通过分析上述符号之间的相关关系可知:
2 模型实证
考虑到对 4 个不同的评价指标进行交通流仿真,因此,在这里需要分别讨论在单一变量下何时达到最优解。
2.1 周边道路等级
周边道路车流量的分布状况等价于其道路等级,故可把该指标转化为易考核性的周边道路等级来仿真。以方形结构、n=4“田”字型出入口以及内部直行和右拐的行驶原则为前提条件,考虑到:有n-2个结点为有效结点,单车道的机动车数量d=21[9],可达度与吸纳密度的转化系数R=1则:

(6)
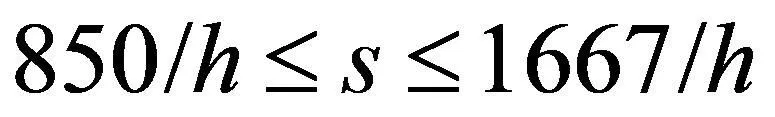
(7)
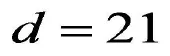
(8)
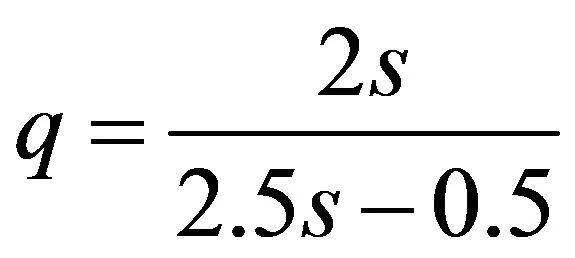
(9)
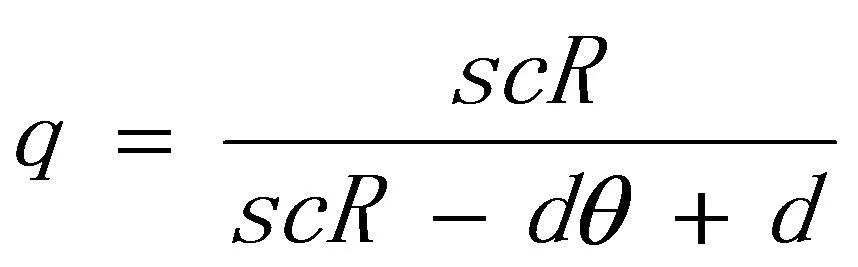
(10)
解得:

(11)
将式(11)的相关结果代入MATLAB随机仿真,得到道路等级随机仿真通过小区的概率,如表1所示。

表1 道路等级随机仿真通过小区的概率
由表1数据分析可知,开放小区对周边道路通行的缓解效果与车道数 大致呈正向相关,且车道数1~2的缓解程度大于车道数2~3。故从节省铺设道路成本的运营商和希望缓解交通压力的使用者2个角度分析:单向车道数 更为合理。
2.2 小区形状结构
以单向车道数k=2、内部直行和右拐的行驶原则为前提条件,考虑到有n-2个结点为有效结点,单行车道的机动车数量d=21,可达度与吸纳密度的转化系数R=1,则:方形、三角形和工字形模块n对应的大小依次为4、3、2,则:
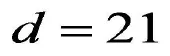
(12)

(13)
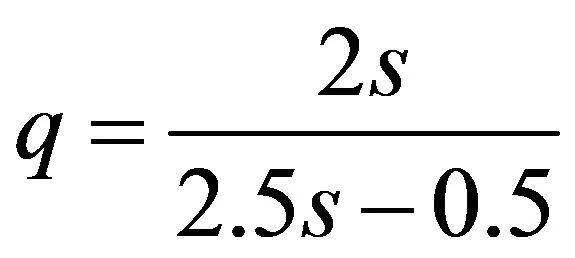
(14)

(15)
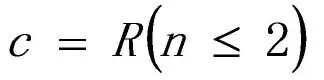
(16)
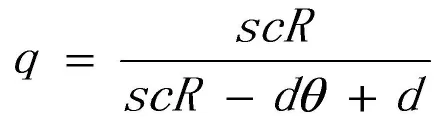
(17)
解得:
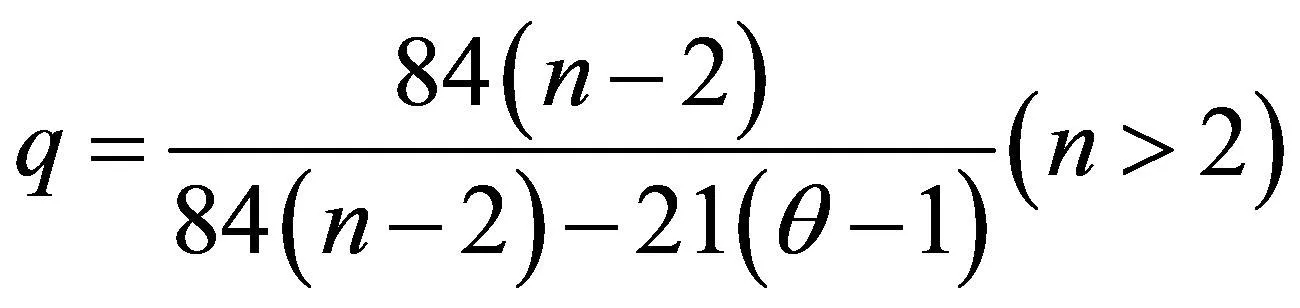
(18)
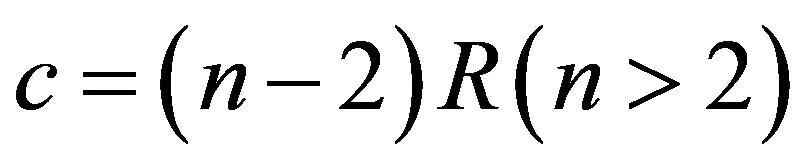
(19)
将式(18)、(19)的相关结果代入MATLAB随机仿真,得到小区结构模型随机仿真通过小区的概率,如表2所示。

表2 小区结构模型随机仿真通过小区的概率
基于以上方形、三角形和工字形3种小区形状,通过排列组合进行拼接,可知:
(1)一与一组合:
由3种基本组成单元自身拼接,则:共有4种方案。
(2)两两组合:
由3种基本组成单元自身与其它两两拼接,则:共有4种方案。但考虑到方案8单元组合形状的特点,没有较大的实际参考意义。故在这里对方案8忽略处理,不再分析。
(3)三三组合:
由3种基本组成单元自身与其它均拼接,则:共4种方案。同样,考虑到4种方案形状的特点,没有较大的实际参考意义,故这里对这4种方案忽略处理,不再分析。
将以上7种组合方案依次重新排序,如图4所示。

图4 7个排列组合方案的形状
由上述分析知:各种方案对应的n大小依次为5、3、4、2、3、3、3。同理,解得:
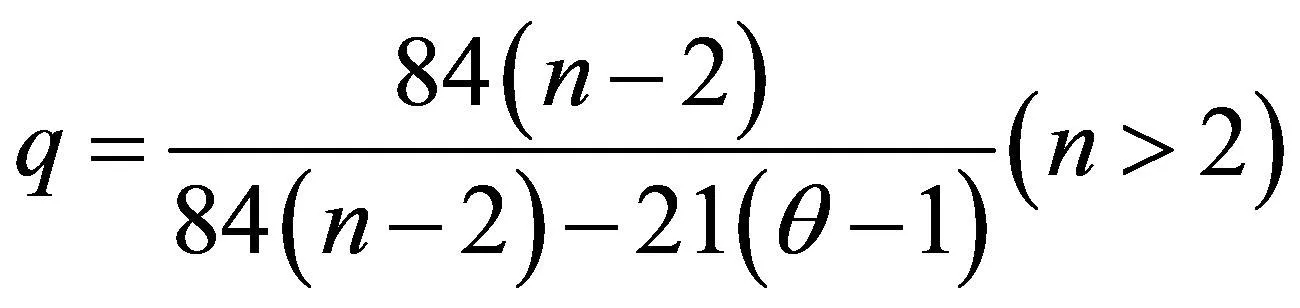
(20)
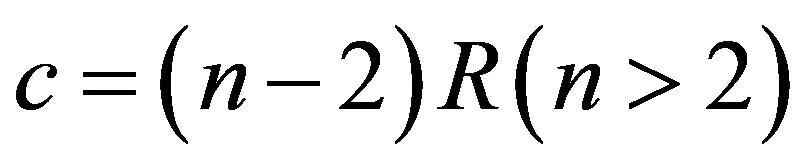
(21)
将式(20)、(21)的相关结果代入MATLAB随机仿真,可知单元组合模型随机仿真通过小区的概率,如表3所示。

表3 单元组合模型随机仿真通过小区的概率
由表3数据分析可知,对于由2个方形拼接的方案1缓解效果均优于其它方案;拼接方案的边数、含有工字形状单元的个数大致与周边道路通行的缓解效果呈负相关。故在该模型中,由方形形状组合的开放小区对其周边道路通行的缓解效果最佳。
2.3 小区面积大小
小区面积大小的差异是由不同数量同种类型的基本单元形状组合造成的,则其等价于道路网的密度。在一定面积的可分域内,小区的面积大小决定了有效结点数。取可分域面积300×300m2、方形单元为例,如图5所示。

图5 3种不同的小区面积形状
其对应的n大小依次为4、6、9、12,则:
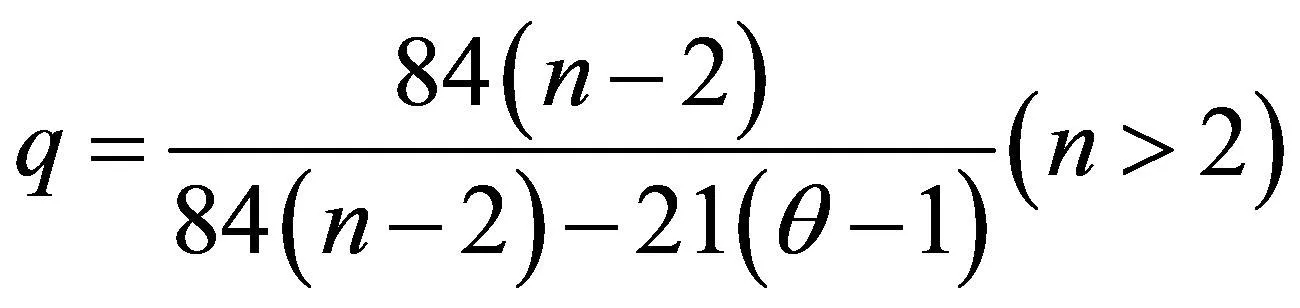
(22)
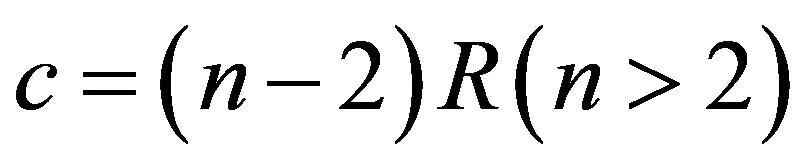
(23)
将式(22)、(23)相应的结果代入MATLAB随机仿真,可知小区面积模型随机仿真通过小区的概率,如表4所示。

表4 小区面积模型随机仿真通过小区的概率
由表4数据分析可知:在单个开放小区面积大致40 500 m2,即:标准方形小区边长大致为97.78 ×158.21 m2更为合理。
2.4 红绿灯时间间隔[10]
以单向车道数k=2、n=4“田”字型出入口及内部直行和左拐为原则的开放小区为前提条件,考虑到有n-2个有效结点,可达度与吸纳密度的转化系数R=1,s=850~1667/h[11],则:

(24)
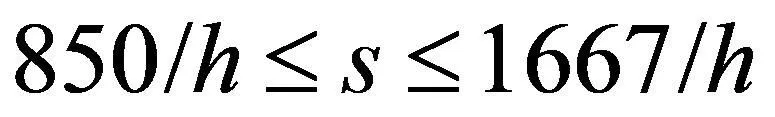
(25)
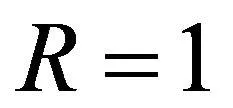
(26)
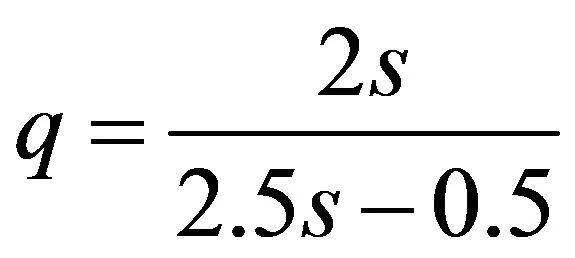
(27)
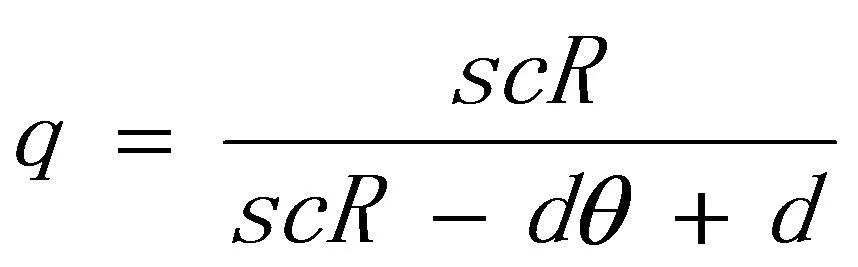
(28)
解得:
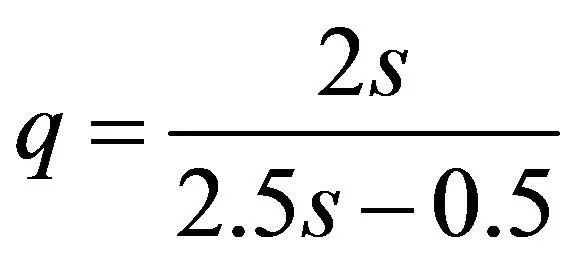
(29)
将式(29)相应的结果代入MATLAB随机仿真,可得车流量模型随机仿真通过小区的概率。

表5 车流量模型随机仿真通过小区的概率
计算相对应的车速控制阀门下的红绿灯时间:
由《道路交通安全法实施条例》[12]第45条可知:取一般的相邻红绿灯间距为800 m,一般的行驶车辆平均车长为5 m,则:

(30)
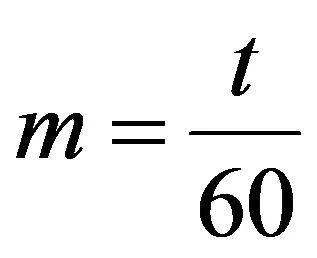
(31)
解得
17.20%≤m≤33.86%
因此,当红灯时间占一个循环周期时间的33.86%时,缓解效果更为明显。
3 结论
(1)分析了交通矛盾、住宅现状和交通流模型的特征。
(2)建立了合理的评价指标体系,并确定出了小区面积、小区形状、周边道路车流量分布和红绿灯时间间隔4个指标与吸纳密度之间的函数关系。
(3)通过模拟仿真得到不同指标下的最优解,使得开放小区在处于此最优解的指标体系下的缓解作用最明显。
[1] 熊烈强,李杰,商蕾等.路段通行能力及其服务水平指标的研究[J].武汉理工大学学报(交通科学与工程版),2004,(04):511-514.
[2] 李向朋.城市交通拥堵对策—封闭型小区交通开放研究[D].长沙:长沙理工大学,2014.
[3] 袁绍欣,赵祥模,安毅生.无信号交叉口车流通行状况的混杂Petri网模型[J].中国公路学报,2010,(01):93-97.
[4] 高海龙,王炜,刘秉轩,等.中国典型地区无信号交叉口临界间隙调查[J].东南大学学报(自然科学版),2000,(03):100-103.
[5] 郑英力,翟润平,马社强.交通流元胞自动机模型综述[J].公路交通科技,2006,(01):110-115.
[6] 翦俊,谭裕安.基于小波分析和傅立叶变换的交通流特性分析[J].科技资讯,2012,(12):241-242.
[7] 贺元香.计算机中的随机函数研究[J].甘肃科技,2008,(20):60-61.
[8] 王永明,周磊山,吕永波.基于元胞自动机交通流模型的车辆换道规则[J].中国公路学报,2008,(01):89-93.
[9] 尤娟娟.我国城市街区型住区规划研究初探[D].重庆:重庆大学,2010.
[10] 薛小平.交通红绿灯控制算法设计与实现[D].长春:吉林大学,2015.
[11] 董怡娜.现代小区交通系统的人性化设计研究[D].长沙:湖南大学,2012.
[12] 中华人民共和国道路交通安全法实施条例[J].中华人民共和国国务院公报,2004,(19):4-17.
Analysis of Application of Cellular Automate Model in Open Housing District
FENG Xian-lei1,WU Yan-wen1,LIU Xuan2,WANG Hong2
(1.College of Electrical Engineering,North China University of Science and Technology,Tangshan Hebei 063210,China;2.College of Science,North China University of Science and Technology,Tangshan Hebei 0639210,China)
open housing district; road capacity; cellular automate; traffic flow simulation
The influence of open community housing districts on the traffic capacity of surrounding roads were researched.Firstly,the indexes of influencing road capacity were analyzed,and then the stochastic simulation of different indexes was carried out by using cellular automate model,which made it reach the optimal solution under single factor variable.The results show that when the plot area is 97.78 158.21 ,the shape is square structure,the surrounding road is bidirectional four lanes,and the red intersection time of road intersection is about 33.86% of the total cycle time,the effect of alleviating traffic by opening area housing districts is more obvious.
2095-2716(2017)03-0038-08
2017-01-08
2017-05-11
国家级大学生创新创业训练计划项目(201410081015);华北理工大学创新创业训练项目(X2016187)。
U121
A

