从一道试题探究圆锥曲线的一组优美性质

北京市第十二中学高中部 (100071) 刘 刚 赵 毅

从一道试题探究圆锥曲线的一组优美性质

北京市第十二中学高中部 (100071)
刘 刚 赵 毅

在2017年1月北京市丰台区高三期末文科数学出了这样一道试题：

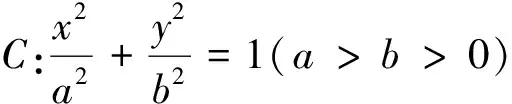
(1)求椭圆C的方程；

(2)过F且斜率为1的直线交椭圆于M，N两点，P是直线x=4上任意一点．求证：直线PM，PF，PN的斜率成等差数列．

试题考查了椭圆的标准方程、几何性质、直线与椭圆的位置关系及坐标法的应用，经过对(2)问的一般化探究及类比推广，可以得到圆锥曲线的一组优美性质．

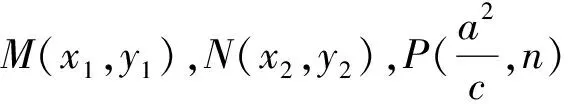
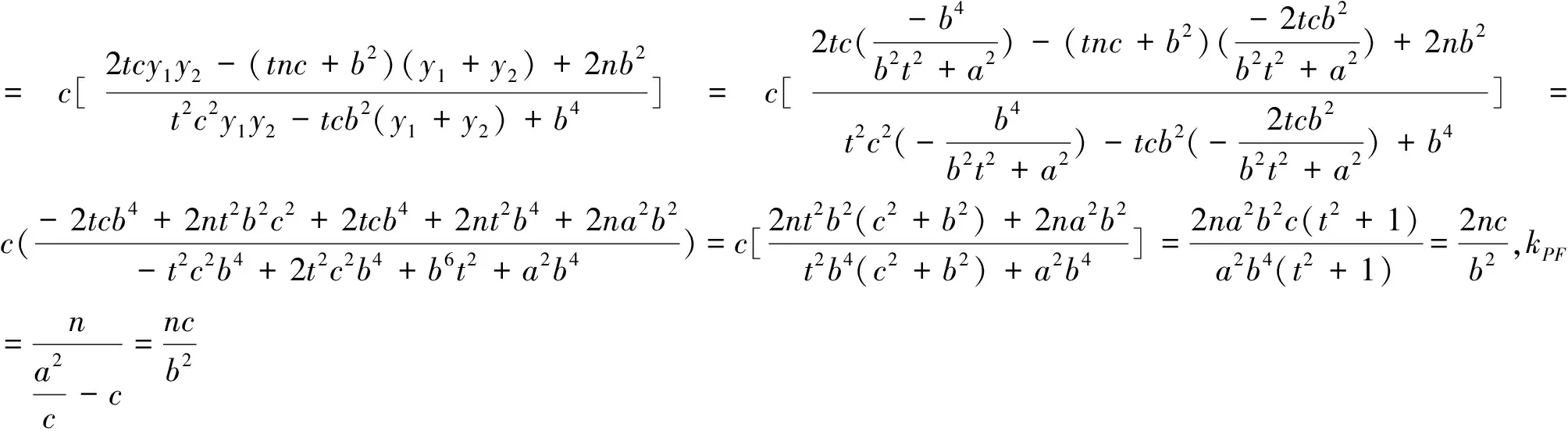
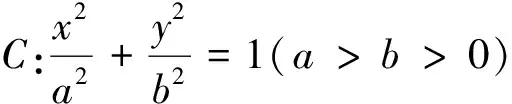
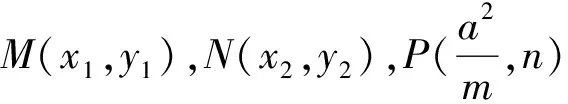
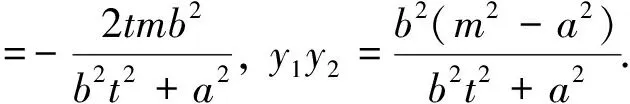
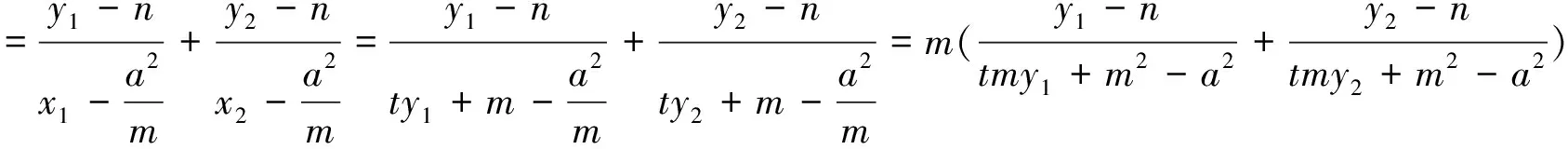
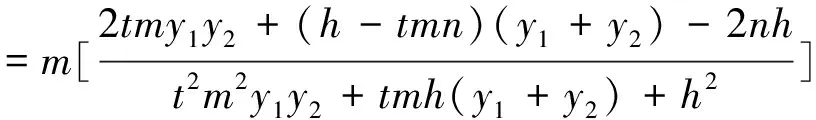
注:当m=c时，性质2就变为了性质1，所以性质1是性质2的特例．另外由椭圆类比到双曲线、抛物线可得性质3与性质4.

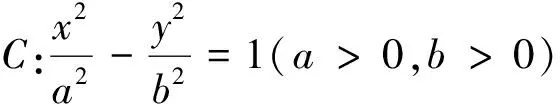
(证明可参考性质2的证明过程，限于篇幅，此处省略)

性质4 过点Q(m,0)(m≠0)的直线交抛物线C:y2=2px(p>0)于M，N两点，P是直线x=-m上任意一点，则直线PM，PQ，PN的斜率成等差数列．

[1]刘刚，赵毅．2016年高考江苏卷数学14题的探究与启示[J]．中学数学研究(江西)，2016，9．

[2]刘刚，赵毅．一道以圆为背景的高三联考试题的探究历程[J]．中学数学研究(江西)，2016，10．

*本文系北京市丰台区“十三五”重点课题《新课程背景下高中数学竞赛教学研究》(课题批准号：2016237-J)阶段成果之一．