涉及三角形角平分线的两个对称不等式

江苏省海头高级中学 (222111) 刘永岩

涉及三角形角平分线的两个对称不等式

江苏省海头高级中学 (222111)
刘永岩

为了书写上方便，下面我们用记号∑表示循环和，如∑a=a+b+c，∑ab=ab+bc+ca等,文[1]给出如下的一个旁切圆与边长的不等式：

已知ra,rb,rc是ΔABC的边a,b,c分别为邻边的旁切圆的半径，则∑(ra-rb)2≥∑(a-b)2.

文[2]给出中线、高与边长的两个不等式：

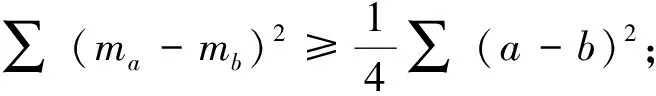
(2)记ΔABC三边为a,b,c，相应边上的中线长为ha,hb,hc,则∑(ha-hb)2≥∑(a-b)2.

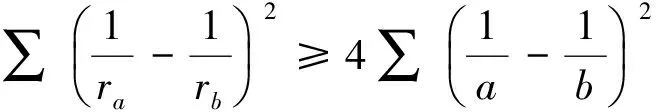
受其启发，笔者得到如下两个不等式：

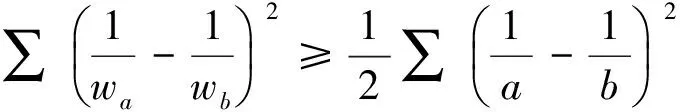
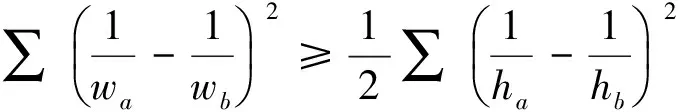
为了证明上述两个不等式，我们介绍下面一个不等式

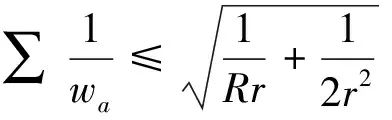
证:根据三角形角平分线公式及柯西不等式，有

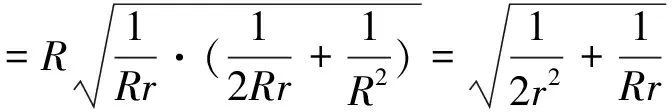
下面我们证明结论1,2:

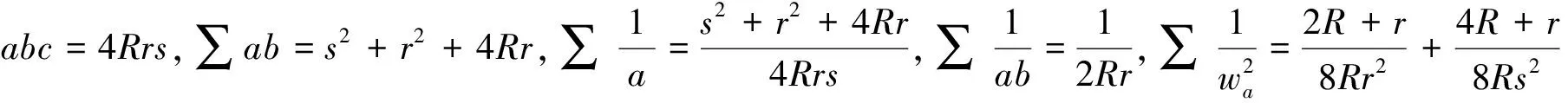
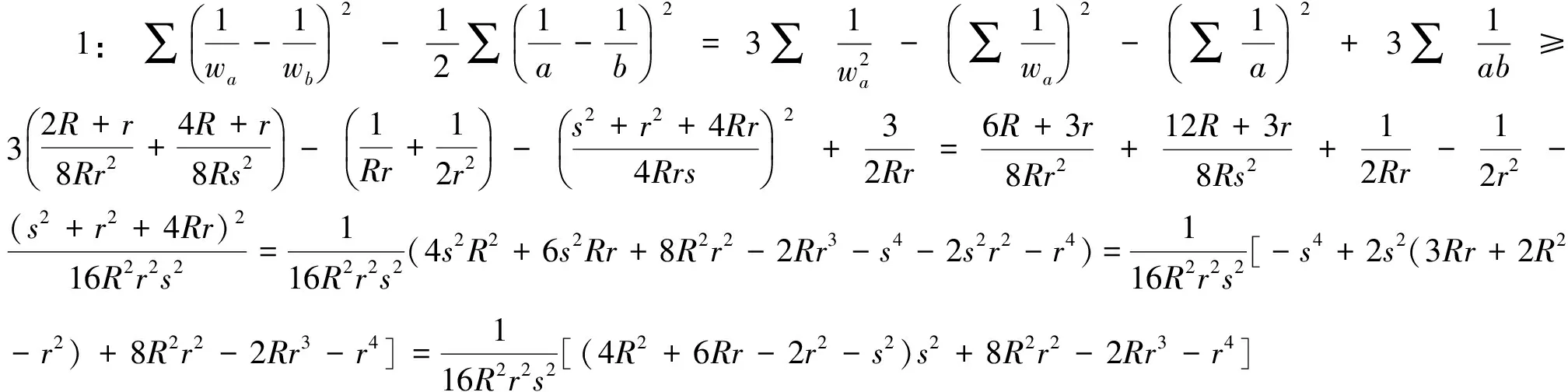
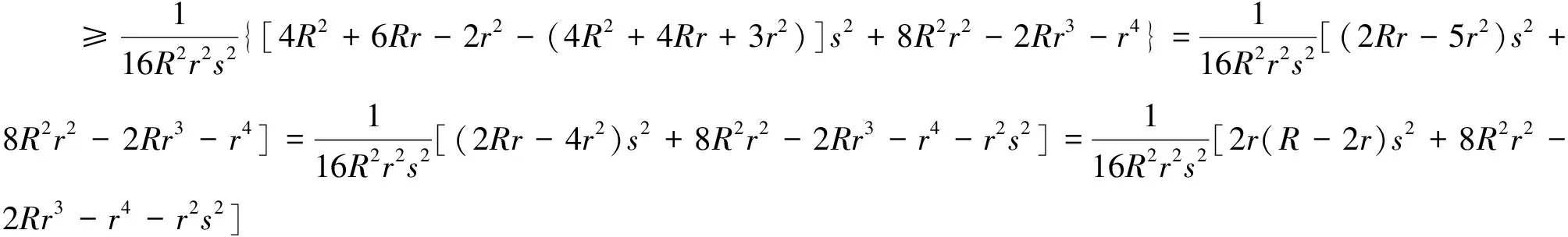
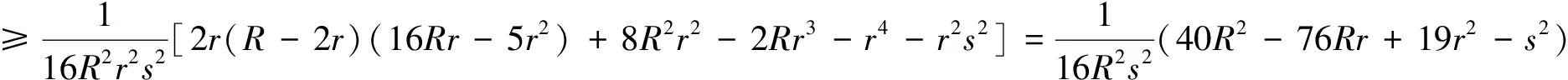
由Gerretsen不等式s2≤4R2+4Rr+3r2,

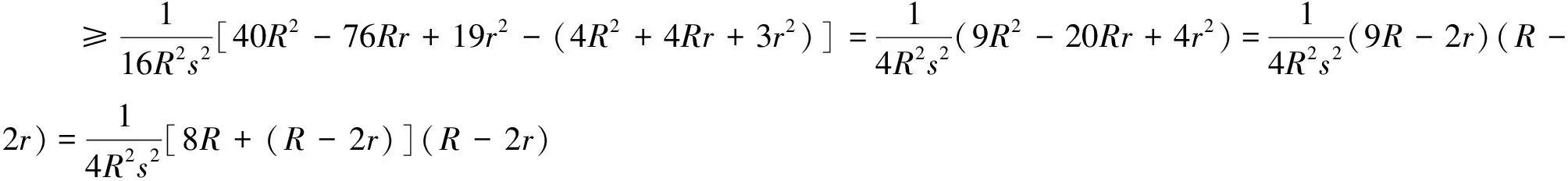
由Euler不等式R≥2r可知④式≥0，故原不等式成立.

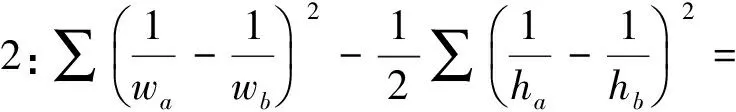
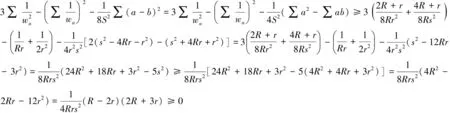
故原不等式成立.

注：此不等式为刘保乾在《110个有趣的不等式问题》[5]中提出的LBQ25(C)问题.

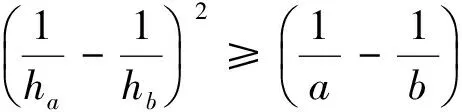
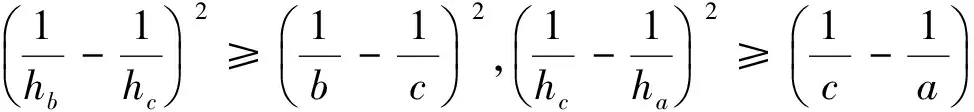
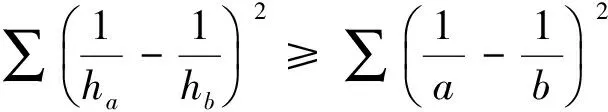
故我们可以得到不等式链

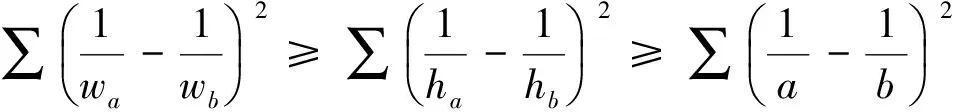
[1]秦庆雄.一个漂亮的几何不等式[J].数学通讯(下半月).2009.6.

[2]侯典峰.两个优美的几何不等式[J].中学数学.2010.6.

[3]董林.对一个优美几何不等式的研究[J].中学数学.2011.2.

[4]杨学枝.关于角平分线的一个不等式[J].数学通讯.1995.8.

[5]杨学枝.不等式研究[M].拉萨:西藏人民出版社,2003.393-394.