合情推理复习课模式——基本不等式中“1”的小专题

江苏省苏州工业园区第二高级中学 (215121) 段赛花

合情推理复习课模式
——基本不等式中“1”的小专题

江苏省苏州工业园区第二高级中学 (215121) 段赛花

数学虽变化万千，但合情推理的教学更加高效.高三二轮复习时间紧任务重，小专题模式以期窥一斑而知全豹，让大家了解复习课利用合情推理是如何高效、简洁地在一节课中解决一类问题.题不在多如何取舍？解一题怎样会一类？笔者重视书本习题的再现和拓展，让学生在各种习题面前抓住本质，以不变应万变.

一、书本原题再现

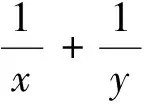
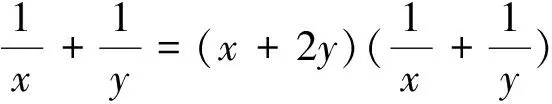
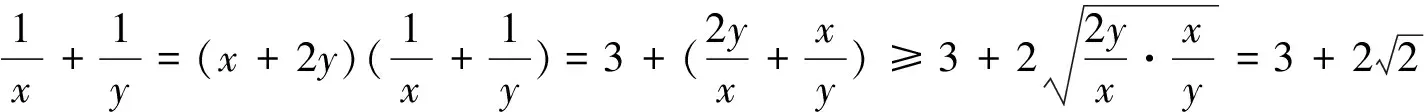
反思：“1”的本质：乘积为定值.

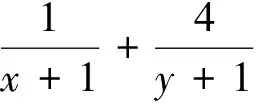
分析：x+y=1，则(x+1)+(y+1)=3,转化为问题1.

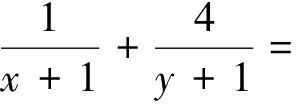
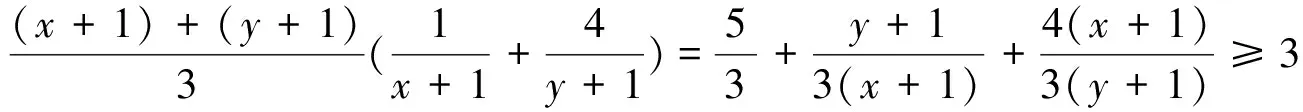
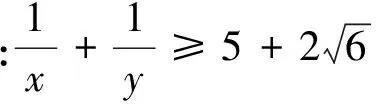
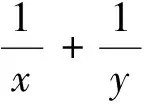
分析：(1)中利用“1”求最值问题转化为证明问题，换个角度，本质一致.(2)解一题会一类，推广到一般情形.

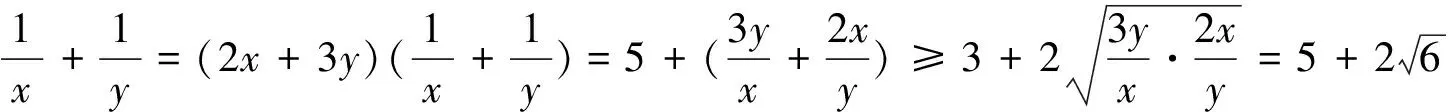
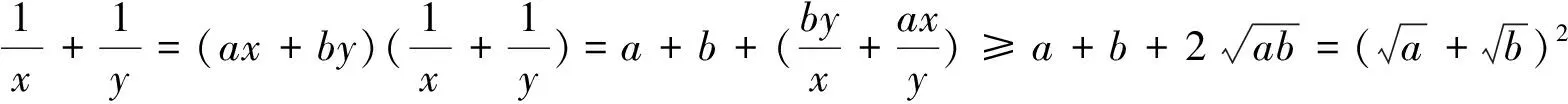
二、“1”的神秘面纱

分析：当“1”不能一眼看穿，利用换元法就能使“1”原形毕露，转化为问题1.

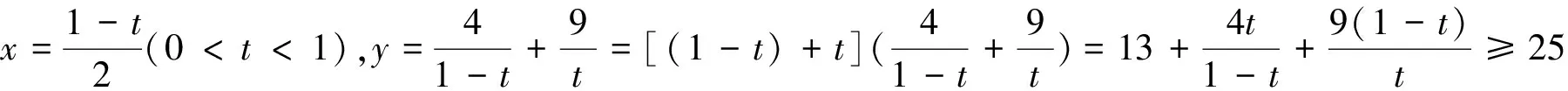
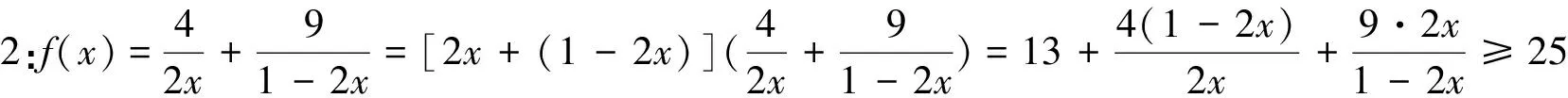
反思：炼就火眼金睛，善于引导学生发现隐含的“1”，事半功倍.

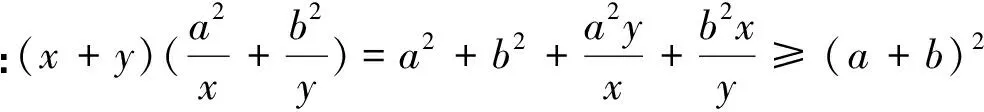
变题2 (苏教版必修5P24，7改编题).已知∠A=60°，P、Q分别是∠A两边上的动点，设AP=x,AQ=y.

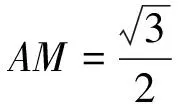
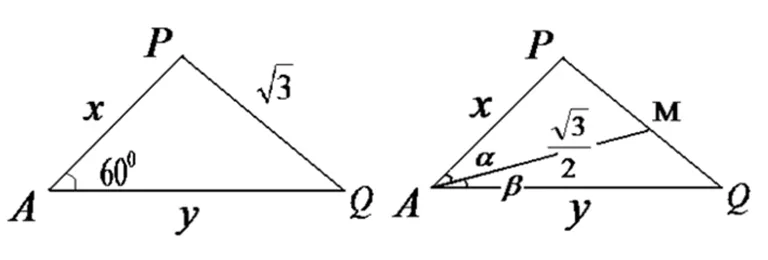
图1 图2

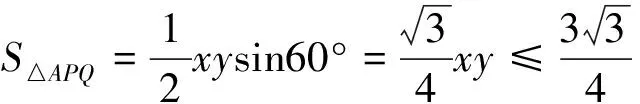
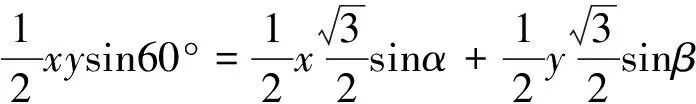
教师点评：本题需要根据等面积法转化抽象出等式，再对等式变形得到关于“1”的式子.此处的“1”很神秘，书本变题尤其关注.

三、“1”的直接代换

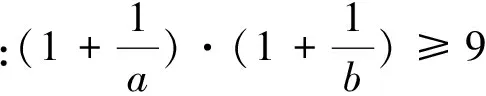
分析：与问题1，2不同的情景，利用“1”的直接代换解决问题.

反思：“1”的直接代换的本质还是乘积为定值.

分析：难点是“1”的直接代换，分类讨论转化为基本不等式求解.

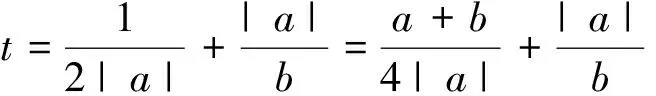
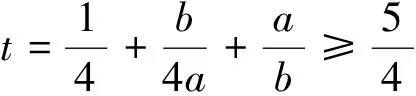
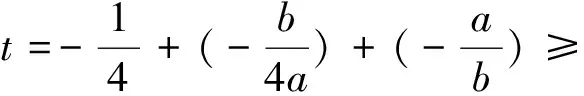
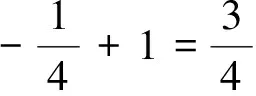
反思：巧用“1”的直接代换，可以轻松解决高考难题.渗透数学思想转化为基本不等式问题.

结合书本习题改编的如下变题可以拓宽学生的思维，让二轮复习的深度和广度得到有效加强.

四、“1”的单双换元

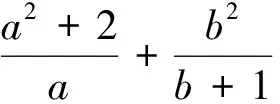
分析：难点：怎样转化为问题1？从得分角度看，学生利用方程思路做，时间来不及，得不到最后结果；从特殊化角度思考，学生普遍认为a=b导致出错.

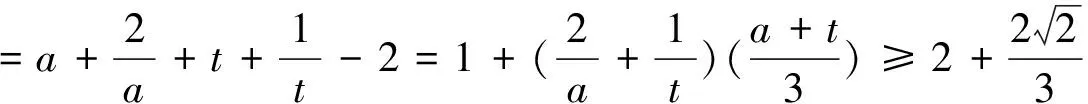
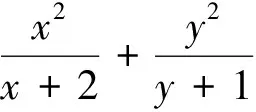
分析：双换元后转化为问题1.学生转化能力有待提高.

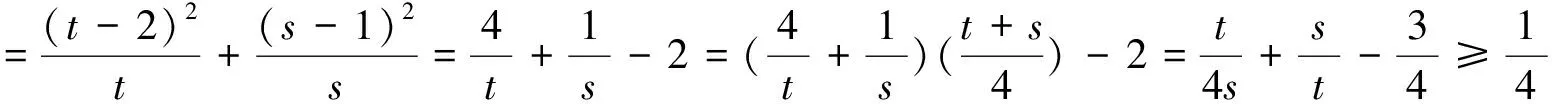
分析：单换元双换元均有困难，想象力和创造力的完美结合.

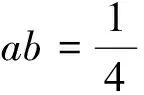
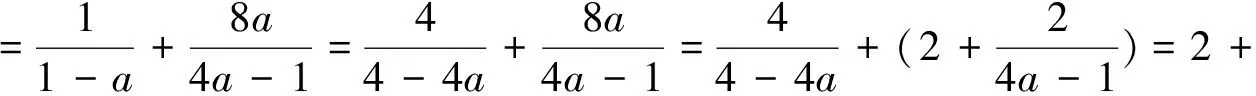
此题是零模考试14题，得分率极低.学生想到求导完成但运算量极大.

教师点评：学生在陌生情境下解题能力怎样提高，关键还是教师平日的变题和编题能力的提高.借助合情推理，从特殊到一般，改变条件，改变结论，收集考试中的一手资料，整理成一个模块，让学生能在一个具体的知识点上完胜！

给你一种解题工具，或现成的概念、定理，或利用已证明的结论，让你配凑与应用来解答某一问题，这是近年高考命题的一种新颖的题型之一，值得我们借鉴与领悟其中的思维本质.合情推理纳入高中教学时间不长，但对学生思维的培养至关重要.叶圣陶倡导“教是为了不教.”学生看清编题者意图，平日多加练习，便能热爱数学，发扬光大.

[1]段赛花.应用题专题复习课模式——三角函数篇[J].中小学数学(高中版).2014(3)：51-54.

[2]段赛花.问渠哪得清如许，为有源头活水来——寻根问源之三次函数切线问题[J].高中数学教与学，2013.

[3]段赛花.走进题根，跨出题海——寻根问源之三次函数极值最值[J].新高考(高三数学)2014,4.

[4]叶圣陶,商金林.中国现代作家作品新编丛书——叶圣陶作品新编[M].人民文学出版社，2013,2.