中国林业全要素生产率的时空差异及空间收敛性分析*

姜钰，管时一

(东北林业大学 经济管理学院，哈尔滨 150040)

中国林业全要素生产率的时空差异及空间收敛性分析*

姜钰，管时一

(东北林业大学 经济管理学院，哈尔滨 150040)

通过构建DEA-Malmquist指数模型和引入收敛性分析的方法，测算了中国林业全要素生产率，分析了林业全要素生产率的区域差异及其变化趋势，以期深化对区域林业全要素生产率的认识和理解，为转变林业经济发展方式及提高林业全要素生产率提供理论支撑。结果表明：⑴2004～2014年林业全要素生产率虽然出现一定的波动幅度，但整体呈上升趋势；⑵各区域林业全要素生产率增长在空间上存在一定的差异；⑶除西藏、北京和青海3个区域外，其他区域的林业全要素生产率都呈增长趋势；⑷由于存在收敛性，各区域之间的差异逐渐减小，以趋于同一水平的趋势发展。

DEA-Malmquist指数法；林业全要素生产率；收敛性分析

林业作为中国国民经济的重要基础性产业，不但会带来经济效益，还会产生巨大的社会效益和生态效益。林业全要素生产率(Forestry Total Factor Productivity，FTFP)是衡量林业经营情况及其功能作用发挥程度的重要指标，不但可以充分体现林业投入产出的能力，还可以反映林业产业可持续发展的能力，因此对林业全要素生产率进行评估具有重要的现实意义。从现有文献来看，国内外专家学者对林业全要素生产率各方面的研究已经很多，研究区域多种多样，但对林业全要素生产率空间变化趋势的研究并不多，其中将林业全要素生产率与收敛性分析相结合的研究更是匮乏，并未准确地把握各区域林业的发展走向[1-5]。这些文献运用的分析方法主要是数据包络分析法(Data Envelopment Analysis，DEA)[6]，它们在指标选取和模型构建方面均为研究奠定了坚实的基础。综合考虑所有因素，选取31个省市2004～2014年的面板数据，在运用DEA-Malmquist指数法[7-11]对区域林业全要素生产率进行测度分析的基础上，进一步对其时空差异和空间收敛性进行分析，判断林业全要素生产率的总体变化趋势以及各区域林业全要素生产率之间的差异，进行收敛性检验，进而根据测算结果提出相关的政策建议。

1 材料与方法

1.1 分析方法

1.1.1 数据包络分析法

每个区域为一个决策单元，共有31个决策单元。已知区域(i)有3个投入指标(j=1，2，3)和2个产出指标(r=1，2)，则xij和yir分别为投入要素和产出要素，则DEA模型为：

⑴

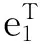
1.1.2 DEA-Malmquist指数法

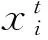
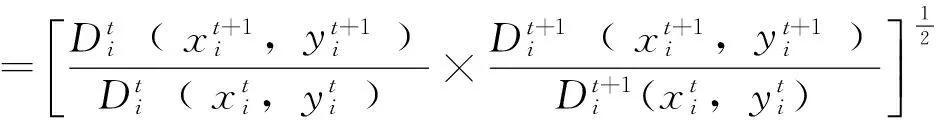
⑵

式中FTFPi﹙xt+1，yt+1；xt，yt﹚表示i区域的Malmquist指数值，若Malmquist指数值大于1，表示t期到t+1期林业全要素生产率有所增长，反之亦然；TECHCH表示林业技术进步变化指数(Technical Change)；EFFCH表示林业技术效率变化指数(Efficiency Change)，在规模报酬可变条件下，EFFCH可分解为规模效率变化指数SECH(Scale Efficiency Change)和纯技术效率变化指数PTEC(Pure Technical Efficiency Change)[7]。

1.1.3 收敛性分析法

新古典理论中收敛性分析的优势在于能够更准确地判断出区域差异的变化动态，因此多应用于区域经济发展之间差距变动情况的研究。收敛性分析方法应用于区域林业全要素生产率差距分析中分别是σ收敛、绝对β收敛和条件β收敛[12-13]。若σt+1<σt，则表明存在σ收敛，说明各区域林业全要素生产率之间存在的差异减小。

⑶

绝对β收敛指在一段时间内，初始期林业全要素生产率低的区域比林业全要素生产率高的区域增长速度更快，各区域的全要素生产率向相同水平发展。若β<0则存在绝对β收敛；反之，则不存在。

⑷

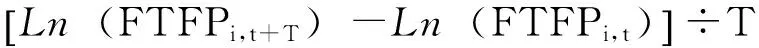
条件β收敛是指在不同区域具有不同稳定的状态的前提下，当各区域都收敛于自身稳定状态时，离自身的稳态越近，其林业全要素生产率增长速度越慢。当且仅当β<0时存在条件β收敛。

Ln(FTFPi，t)-Ln(FTFPi，t-1)=α+βLn(FTFPi，t-1)+ε

⑸

式中Ln(FTFPi，t-1)与Ln(FTFPi，t)分别表示第i个区域分别在第t-1时期和第t时期林业全要素生产率的对数值；α为常数项；β为未知系数；ε为误差项。

1.2 指标选取

DEA-Malmquist指数法最关键的环节之一是选取投入产出指标，国内外的相关研究中有关林业产业投入产出指标的选取方式多种多样[14-16]，模型中投入产出指标构成如表1所示。林业投入要素主要分为土地、资本和劳动三大类。由于林地面积是最直接反映林业在土地方面投入多少的指标，所以选择林地面积作为一项投入指标。在资本和劳动力方面，考虑到数据的可获得性，选择固定资产投资完成额和林业系统年末从业人数作为投入指标。林业产出指标主要从生态和经济两方面进行选取，分别为森林蓄积量、林业总产值。

表 1 模型中投入产出指标

1.3 数据来源

指标数据来源于2004～2014年《中国林业统计年鉴》中全国森林资源情况、林业产业总产值、各地区林业系统单位年末人数和各地区林业固定资产投资完成情况。其中部分数据缺失，《中国林业统计年鉴》对此现象做出了说明，即“表示数据不足本表单位数、不详或无该项数据”。采用相邻年份数据的均值对缺失数据进行补充。

2 结果与分析

2.1 林业全要素生产率的时空差异

2.1.1 2004～2014年林业全要素生产率的总体趋势

首先运用DEA-Malmquist指数法对面板数据进行处理，然后从时间上对处理得到的结果进行分析，

表 2 2004～2014年林业全要素生产率DEA-Malmquist指数及其分解

Table 2 Forestry total factor productivity DEA-Malmquist index and its components between 2004 and 2014

年份PTECSECHTECHCHFTFP2004～20051.0540.9861.0331.0742005～20061.0260.9881.0091.0222006～20071.0920.9581.0321.0792007～20080.9461.0071.0841.0332008～20091.0581.0400.9201.0132009～20100.8860.9381.3991.1632010～20111.2640.7971.5981.6112011～20121.0281.1620.8441.0092012～20131.0111.0901.1031.2162013～20140.9570.9491.1051.004

结果如表2所示。2004～2014年中国林业全要素生产率具有一定的波动性，在2010～2011年中国林业全要素生产率增长达到最高点，在此期间上涨了61.1%，中国林业全要素生产率增长的最低点出现在2013～2014年，在此期间仅增长了0.04%。由此可见，2004～2014年中国林业全要素生产率整体呈上升趋势，其中2008～2009、2011～2012、2013～2014年中国林业全要素生产率的增长趋势较为缓慢。2008年受严重台风、暴雨引发的洪涝灾害和春季大兴安岭特大森林火灾以及北方低温冷冻和雪灾的影响，中国林业产业受到了较大的创伤；而且2008年美国爆发的次贷金融危机引发了全球金融危机，导致全球经济遭受重创，林业经济也受到严重冲击、无法实现资源的合理配置、发展异常艰难，致使2008～2009年林业全要素生产率增长缓慢。随着天保二期工程的实施，林地面积得到保护，但是2012年和2014年林业工作者数量减少，林业固定资产投入降低，且林业一二产业的产值明显降低，导致2011～2012年和2013～2014年林业全要素生产率发展缓慢。

2004～2014年中国林业全要素生产率及其3个构成要素的变化情况如表2所示。纯技术效率指数始终保持稳定在1.000上下浮动，说明该指数的变化趋势保持稳定状态；规模效率波动幅度较小，除了2010～2012年出现小幅度波动外其他时间一直处于较稳定状态；技术进步指数的波动性较强，从变动趋势中可以看出，技术进步指数的变动趋势与全要素生产率指数的变动趋势较一致。由此可见，规模效率和纯技术效率对中国林业全要素生产率的影响较小，林业全要素生产率主要是受技术进步变动的影响。

2.1.2 林业全要素生产率的区域比较分析

DEA-Malmquist指数不仅从时间上对林业全要素生产率进行了阐述，而且其结果可以对各区域之间林业全要素生产率进行空间比较(表3)。技术进步、纯技术效率和规模效率共同作用对各区域林业全要素生产率产生影响。2004～2014年，规模效率下降1.3%，由于纯技术效率和技术进步分别上涨2.8%和9.5%，在三者共同作用下林业全要素生产率上涨了11.1%，林业全要素生产率总体呈上升趋势。2004～2014年，全要素生产率的平均年增长率为11.1%，增长幅度较大。其中广东省的林业全要素生产率增长年均幅度最大，达到31.7%；山东省以25.5%的增长率排在第二位，辽宁、江苏和重庆的年均增长率同为21.7%，同时位列第三位。虽然大部分区域林业全要素生产率发展趋势良好，但仍有少数区域林业全要素生产率呈现负增长趋势。其中西藏地区林业全要素生产率下降最多为10.6%，其次依次为北京(1.3%)和青海(1.1%)。北京区域林业产业资源并不丰富，且注重经济的快速发展，无法发展有规模的林业产业。青海和西藏皆属于欠发达地区，这两个区域在全国经济发展排名中部偏后，并且受到天保工程的影响，禁止和限制砍伐木材，导致林业产出下降，致使这两个区域林业全要素生产率出现负增长情况。

表 3 各区域林业全要素生产率DEA-Malmquist指数及其分解

说明：表3中每个数据均为2004～2014年变化的平均值。

2.2 收敛性分析

2.2.1σ收敛检验

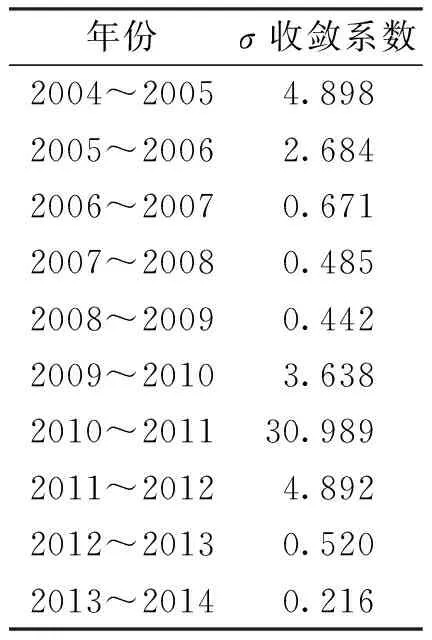
根据式⑶可求得每年林业全要素生产率的σ收敛检验系数，根据其变化趋势判断是否收敛(表4)。中国区域林业发展大致分为3个阶段：第一阶段(2004～2009年)存在显著的σ收敛，这一阶段中各区域林业全要素生产率之间的差异逐渐变小，σ收敛系数由4.898降低至0.442，下降了90.98%。这一结果表明，在这段期间全国各区域林业全要素生产率的差异从最初的高度降到一个趋于稳定的程度。第二阶段(2009～2011年)属于发散阶段，各区域林业全要素生产率的差异明显加大。由于这期间全世界正处于美国次贷危机引发的全球金融危机时期，政府采取的应对全球经济危机的救助措施，使中国各区域的林业经济发展受到不同程度的影响，打破了原有的稳定状态，导致各区域林业全要素生产率这几年差异增大。第三阶段(2011～2014年)σ收敛性显著，各区域林业全要素生产率的差异逐渐减小，又一次趋于稳定状态。随着金融危机的离去和政府宏观调控手段的运用，各区域林业经济的发展得到恢复，林业全要素生产率正向同一水平迈进。

2.2.2 绝对β收敛检验

为了深入了解各区域林业全要素生产率的收敛性，进一步采用β收敛检验。因为在σ收敛检验中得出的林业全要素生产率的变动情况可以分为3个阶段，所以将区域林业全要素生产率的绝对β收敛分为总体时间跨度和3个时间段进行检验。检验结果(表5)表明：所有β回归系数均通过5%的显著性检验，β值均为负数，说明对于不同时段的区域林业全要素生产率均存在绝对β收敛。2004～2014年各区域林业全要素生产率增长速度为24.3%。从不同的时间段来看，收敛速度也存在较大的差异。第一阶段(2004～2009年)收敛速度最快，达到28.8%，说明林业欠发达区域林业全要素生产率的增长速度明显快于林业发达区域。第二阶段(2009～2011年)收敛速度降到最低，达到2.2%，说明林业欠发达区域和发达区域的林业全要素生产率增长速度几乎相同。第三阶段(2011～2014年)收敛速度略有回升，为23.7%，说明林业欠发达区域林业全要素生产率的增长速度快于林业发达区域林业全要素生产率的增长速度。

表 4 林业全要素生产率σ收敛系数变化趋势

Table 4 Theσconvergence coefficient change trend of regional forestry total factor productivity

年份σ收敛系数2004～20054.8982005～20062.6842006～20070.6712007～20080.4852008～20090.4422009～20103.6382010～201130.9892011～20124.8922012～20130.5202013～20140.216

2.2.3 条件β收敛检验

与绝对β收敛不同之处在于条件β收敛是衡量各区域林业全要素生产率是否收敛于自身水平。条件β收敛检验分析需要运用31个区域的面板数据，借助Eviews软件进行操作，得到条件β收敛回归系数如表6所示。Sig.值全部为0，说明在1%的显著性水平下，无论是总体上还是各阶段之间，区域林业全要素生产率均存在很强的条件β收敛性。存在显著的条件β收敛是指随着时间的推移，各区域林业全要素生产率会收敛于自身的稳定水平，且离自身的稳定水平越近，该区域林业全要素生产率的增长速度越慢。随着各区域之间文化交流的逐渐加强和经济合作的不断深入，各区域林业全要素生产率的增长差异逐渐减小，从而使中国林业在总体上收敛于相同稳定增长水平。

表 5 林业全要素生产率绝对β收敛检验表

Table 5 Regional forestry total factor productivity absoluteβconvergence test table

时间跨度β值标准差Sig.2004～2014年-0.2430.0590.000第一阶段-0.2880.0600.000第二阶段-0.0220.1320.034第三阶段-0.2370.0840.009

3 结论与建议

表 6 林业全要素生产率条件β收敛检验表

Table 6 Regional forestry total factor productivity conditionβconvergence test table

时间跨度β值R2F检验值t检验值2004～2014年-2.2390.76216.726-25.641第一阶段-2.1750.7415.938-15.743第二阶段-2.3780.5973.274-7.853第三阶段-2.2960.83414.573-21.245

3.1 结论

第一，2004～2014年林业全要素生产率年均增长11.1%，技术进步年均增长9.5%，技术进步指数的变动趋势与全要素生产率指数的变动趋势较一致，林业全要素生产率的变化主要是受技术进步的影响，技术进步主要体现在以电子商务为特征的营销方式创新、以集体林权为特征的制度创新和以平衡根系育苗等技术为特征的技术创新等；第二，各区域林业发展水平存在一定差异，这与各区域自身生态环境的状况、科技水平的高低和区域政策的执行力度等密切相关；第三，林业全要素生产率只有2009～2011年σ收敛检验发散，其他所有阶段各种收敛性检验均存在显著收敛，表明随着时间的推移，存在林业全要素生产率低的区域对林业全要素生产率高的区域的“追赶效应”，各区域林业全要素生产率之间的差异逐步缩小，这可能是林业技术水平不断提高、发展区域林业特色产业、加强区域间交流合作的结果。

3.2 建议

3.2.1 加强区域间交流合作，促进全要素生产率增长

要充分了解各区域间林业全要素生产率存在的差异。对于自然资源、地理位置和科技水平相似，但全要素生产率存在很大差异的地区，如天津和北京，可以定期开展经验交流会，通过林业全要素生产率高的区域带动林业全要素生产率低的区域，最终实现各区域林业共同发展。对于各环境状况相似，全要素生产率水平相近的区域，如青海和西藏，可以组织林业科技人员集体培训和开展友谊竞赛，激励各区域加强林业建设。对于黑龙江、内蒙古等森林资源丰富，林业全要素生产率增长缓慢的区域，可将国家林业局开展的援青援藏行动进行拓展，分享政策红利。

3.2.2 依靠因地制宜等方法，促进林业健康发展

因地制宜制定林业发展策略，大力推进各区域林业快速发展，是基于各区域林业发展状况存在一定差异的现状提出的对策。研究结果中可以看出，全要素生产率增长较快的区域经济水平比较发达，林业经营的机会成本较高。因此，可以加大林业补贴力度，完善林业改革，保护林农对林业资产的收益和处置权，提高农民林业经营的积极性。西部地区整体林业发展缓慢，应完善林业基础设施建设，引进高新技术设备，充分发挥林业资源优势大力发展林下经济。对于东北区域，可以大力开展生态旅游，在产业布局和产业规模上发挥优势，制定“一县一业”的政策，促进林业经济的快速发展。

3.2.3 推进科技成果推广，加快林业技术效率提升

林业全要素生产率不仅受林业技术进步的影响，还受林业技术效率的制约。因此，应大力推广科技成果的应用，加快林业技术效率的提升。第一，发挥现代媒体作用，利用网络、电话和广播等媒体的传播作用，宣传促进林业发展的新技术，便于低全要素生产率区域对新技术的接收和学习，有利于促进这些区域的林业发展。第二，运用技术培训方式，通过定期或不定期的技术培训，推进低全要素生产率区域林业技术的普及，提升该区域技术人员处理技术难题的能力，为该区域林业健康稳定发展提供保障。

[1]臧良震，张彩虹．中国林业全要素生产率的时空格局演化研究[J]．统计与决策，2016(8)：118-122．

[2]黄安胜，刘振滨，许佳贤，等．多重目标下的中国林业全要素生产率及其时空差异[J]．林业科学，2015，51(9)：117-125．

[3]张自强，李怡．营林业全要素生产率增长的测算及其分解：来自27个省级面板数据的分析[J]．干旱区资源与环境，2016，30(12)：89-94．

[4]陈晓兰，姜雪梅．中国林业全要素生产率分析[J]．林业经济，2014，37(3)：75-82．

[5]张颖，杨桂红，李卓蔚．基于DEA模型的北京林业投入产出效率分析[J]．北京林业大学学报，2016，38(2)：105-112．

[6]CHARNES A，COOPER W W，LEWIN A Y．DateEnvelopmentAnalysis：Theory，Methodology，andApplications[M]．Dordrecht，Boston and London：Kluwer Academic Publishers，1995：153-154．

[7]FARE R，GROSSKOPF S，LOVELL C A K．ProductionFrontiers[M]．New York：Cambridge University Press，1994：128-130，246-249．

[8]姜博骞，刘欣．基于DEA-Malmqusit的环渤海经济区水资源利用效率评价[J]．资源开发与市场，2015，31(1)：49-51．

[9]ILIYASU A，MOHAMED Z A，HASHIM M．Productivity growth，technical change and efficiency change of the malaysian cage fish farming：an application of malmquist productivity index approach[J]．AquacultureInternational，2015，23(4)：1013-1024．

[10]田杰，姚顺波．中国林业生产的技术效率测算与分析[J]．中国人口·资源与环境，2013，23(11)：66-71．

[11]吴俊媛，苏时鹏，许佳贤，等．林改后农户林业全要素生产率变动测算与分析：基于DEA-Malmqusit指数方法以浙江丽水为例[J]．林业经济，2013(1)：51-55．

[12]毛伟，赵新泉，居占杰．纳入土地要素的中国全要素生产率再估算及收敛性分析[J]．资源科学，2014，36(10)：2140-2148．

[13]屈玉阁．中国船舶工业生产率增长及收敛性研究：基于2005-2012年15个省份面板数据的分析[J]．河北经贸大学学报，2014，35(3)：116-120．

[14]李桦，姚顺波，刘璨，等．集体林分权条件下不同经营类型商品林生产要素投入及其效率：基于三阶段DEA模型及其福建、江西农户调研数据[J]．林业科学，2014，50(12)：122-130．

[15]臧良震，支玲，郭小年．中国西部地区林业生产技术效率的测算和动态演进分析[J]．统计与信息论坛，2014，29(1)：13-19．

[16]徐道炜，刘金福，洪伟．近20年中国林业系统自然保护区投入产出效率评价[J]．福建农林大学学报(自然科学版)，2015，44(3)：276-281．

10.16832/j.cnki.1005-9709.2017.02.016

2016-10-12 基金项目：黑龙江省哲学社会科学研究规划项目(16JYB07)、中国博士后科学基金面上资助项目(20090460871)

姜钰(1978-)，女，黑龙江哈尔滨人，教授，博士，从事林业经济统计方面的研究，(电话)0451-82190381，(E-mail)jy666abc@126.com。

F326.299

A

1005-9709(2017)02-0086-06