军用飞机机群战备完好性研究*
李军亮,滕克难,徐吉辉,夏菲,李季颖
(1.海军航空工程学院,山东 烟台 264000;2.中国人民解放军92635部队,山东 青岛 266041;3.国网辽阳供电公司,辽宁 辽阳 111000)
军用飞机机群战备完好性研究*
李军亮1,2,滕克难1,徐吉辉1,夏菲3,李季颖1
(1.海军航空工程学院,山东 烟台 264000;2.中国人民解放军92635部队,山东 青岛 266041;3.国网辽阳供电公司,辽宁 辽阳 111000)
综合考虑任务要求、保障对象、保障系统三者之间的运行机理,建立了一种基于任务驱动的机群战备完好性仿真模型。以作战任务要求和机群技术状态为输入,进行O&MTA,建立逻辑确定而工期随机的PERT网络,分析PERT网络中各节点和路径上的维修时间、备件延误时间、资源组等待时间的分布函数和参数,然后用Monte Carlo仿真确定成为关键路径概率最高的路径为关键路径,最后用Monte Carlo方法对选定的关键路径进行计算,得出机群装备战备完好率随着保障时间的变化曲线。计算结果表明该仿真模型可以较好反映不同任务要求与保障系统下机群可用性的真实情况,为装备的作战使用提供较好的决策依据。
机群;战备完好率;PERT网络;蒙特卡罗;维修;保障
0 引言
战备完好能力与性能是装备同等重要的战术技术指标,也是综合保障的重要目标,表征装备在任务前是否可用。武器装备战备完好性指标一般选用战备完好率或者使用可用度[1-15],也有部分学者在研究过程中采用装备完好率来表示武器装备的战备完好性[16-18]。
文献[1-3]分别给出了战备完好性的定义与战备完好率的评估模型。文献[4]通过仿真方法分析如何通过联合保障提高A-4飞机的战备完好性。文献[5]给出了在给定维修保障方案下k/N系统的使用可用度模型。文献[6]给出了一种机群战备率的评估方法。文献[7-8]对飞机可用度、备件保障度等评估模型进行研究。文献[9]综合考虑军用飞机任务需求、初始使用和设计阶段的保障方案等信息,利用Monte Carlo方法和排队论构建模型,获得一族使用可用度与RMS参数的关系曲线。文献[10]研究任务期间很难修理或者不能修理的复杂武器装备在任务准备期的战备完好率评估模型,文献[11]在此基础上,分析了任务准备阶段飞机修复时间与备件满足率、备件供应时间、故障件的修理时间等保障因素的关系,给出了服从一般分布修复时间函数,建立了在给定任务通知时刻的战备完好率模型,但是在修理时间的计算上,没有考虑O&MTA,仅选取故障单元中最大的维修时间为修复时间。文献[12-13]考虑维修保障和备件保障两个方向考虑了备件和维修的延误,建立了平均维修延误时间和平均备件延误时间计算模型。文献[14]导出了备件在定期补充方式下的备件供应体制为两站制和三站制的备件延误时间模型,用现场更换模块(LRU)的可靠性、维修性、备件保障性(RMS)参数来表达可靠性串联结构的系统战备完好率模型。文献[15]考虑任务执行过程中运行时间和维修时间的约束,提出一种k/N机群任务可用度模型的解析式,但只考虑了在一个维修组工作的情况,即所有工作串联进行。文献[16-18]通过对机群的完好率进行研究,针对完好飞机,重点研究飞行批次对完好率的影响;对于故障飞机,重点研究中修级维修和串件维修对修复率的影响,进而得出在基层级维修能力下机群满足总体完好率要求的持续时间。
但是装备完好性的度量涉及到装备的可靠性、维修性、测试性以及保障性等,是一个复杂的系统工程,由于研究角度不同,考虑的重点不一样,所建模型往往带有一定的局限性:
首先,大部分文献计算战备完好率时,比较注重装备的修复性维修和使用保障工作,很少有提到预防性维修,只有文献[12,14]有所涉及。其次,在计算故障装备修复时间时,一是未考虑维修保障工作的逻辑关系,仅计算各个部件的维修时限,从中选取最大值;二是对维修保障资源配置情况考虑不充分,研究较多的是备件的供应问题对维修时间的影响,没有分析维修保障系统对装备修复时间的影响。
本文以作战任务要求为输入,分析机群装备的技术状态、装备保障系统的保障能力,通过O&MTA建立机群保障任务的PERT图,然后对PERT网络上的各个节点特性进行分析,采用Monte Carlo对PERT的关键路径上的保障工期进行仿真得出机群装备战备完好率。
1 问题分析
面向任务的机群装备战备完好率计算就是在给定的训练任务或者作战任务条件下,通过分析机群的可靠性、维修性、保障性的相关因素,根据现有的装备状态、资源配置和保障条件,通过军用飞机使用作业流程,计算出机群在任务准备期结束时的战备完好率,基本过程如图1所示。
2 建模分析
基本模型主要包括作战任务模型、随机维修保障网络(stochastic maintenance task net),维修保障工作时间分布函数、备件延误时间函数、资源组等待时间分布函数等。
2.1 作战任务模型
作战任务要求是计算战备完好率的顶层输入,军用飞机执行不同任务时对应不同放飞标准,不同放飞标准对应不同最小设备清单,所以任务要求决定装备的使用方案和使用要求,进一步决定保障要求。目前关于作战任务的概念和描述可以分为2类:第1类是在任务空间概念模型中对作战任务的描述[19],从预期作战应用的角度,强调任务执行的具体过程,体现为作战使命的组成部分;第2类是通用联合作战任务清单中对作战任务的描述[20],从执行主体的角度,强调任务本身是一种能力,由执行任务的作战单元决定,用以确定达成使命的能力需求。文献[21]建立了飞机作战单元的任务要求到装备保障要的转化模型,并以任务清单的形式描述任务要求,如表1所示。
表1中所包含的任务参数可以完整描述出装备在使用过程对应的时间维、逻辑维和专业维的要求,从而实现对任务要求到保障要求转换的输入。
2.2 基于PERT的随机维修保障网络分析
维修保障随机网络(SMTN)采用工程网络计划技术(PERT),基于保障工作项目中保障资源、保障组织和保障流程的约束,来建立保障活动间的邻接逻辑关系确定而工期随机的网络图[22-23],各项活动的工期持续时间主要受维修保障时间、等待时间和延误时间等要素的影响,每一项的保障活动持续时间都具有随机性。
对于PERT图中节点分析的实质是对装备在保障过程中任务剖面的分析,主要分析的因素有保障活动的维修时间、备件延误时间及资源组等待时间的分布类型及参数,而这些要素的分析其实是对保障系统资源配置情况和保障效能的直接反映。常用的维修时间分布类型主要有正态分布、指数分布、对数正态分布等[22],计算公式和使用规律如表2所示。

参数种类任务威胁任务目的任务主体任务时间任务空间任务方式任务参数敌作战力量、目的、行动方向 ……作战目标作战效果任务量 ……编制情况动用情况战技术性能可靠性维修性开始时间结束时间持续时间最早开始时间 ……作战区域战场环境作战方向……作战类型作战样式基本战法执行方式……

表2 常用维修活动的分布形式Table 2 Classic distribution function of maintenance time
在机务保障过程中一般按照维修专业进行保障,以故障简单、单一产品的维修活动或基本作业为主,所以假设维修活动分布服从正态分布。
在保障过程中,备件延误时间Tsi主要和备件失效率、平均保障率、周转时间等因素相关,其计算方法可由式(1)表示[12-13]为
(1)
式中:λ为部件的失效率;ts为任务持续时间;Ps(m,λ,t0)为平均备件保障率;m为现场备件数量;tp为当现场缺少备件时得到备件的周转时间;t0为补充备件周期中累计的工作时间。
资源组等待时间主要是指在装备维修或者保障过程中,由于维修装备、设施或者器材等因素的约束不能及时开展保障活动而产生的等待时间为
(2)

2.3 基于MC的仿真的战备完好性仿真流程设计
MonteCarlo技术作为一种数字仿真方法,在处理复杂系统问题的过程仿真上能体现出巨大的优势。采用蒙特卡洛技术对SMTN的工期进行仿真,从而得出任务准备期内的机群装备可用性曲线,具体步骤如下:
步骤1:建立保障项目的维修PERT图;
步骤2:根据O&MTA结果确定网络节点上需要的保障资源类型和数量;
步骤3:计算各工序的持续时间T(i,j),T(i,j)=t(i,j)+Ti。其中,t(i,j)为工序的维修保障时间,可由表2给出的公式计算,Ti为延误时间,可由式(1),(2)计算;
步骤4:根据军用飞机在实际使用过程的统计数据,计算各工序节点上所需时间的均值和标准差;
步骤5:对PERT网络上的每条路径采用MonteCarlo仿真,仿真1 000次记录每次仿真结果,统计出成为关键路径概率最高的路径为关键路径;
步骤6:用MonteCarlo方法对步骤5中选定的关键路径进行仿真,进而进行基于仿真结果的任务工期概率特性分析;
步骤7:输出结果。
3 案例分析
假设某次任务间隙,机群在位飞机6架,完好飞机3架,不完好飞机3架,需要出动4架飞机执行任务,每架任务持续时间(飞行时间)不小于2h,装备准备时间为2h。根据图1所示流程,选用装备使用方案。各架飞机对应的维修、保障任务清单如表3所示。
飞机1为故障飞机,需要更换进行左起落架机轮、进气道防冰活门、微动开关x以及机务准备和武
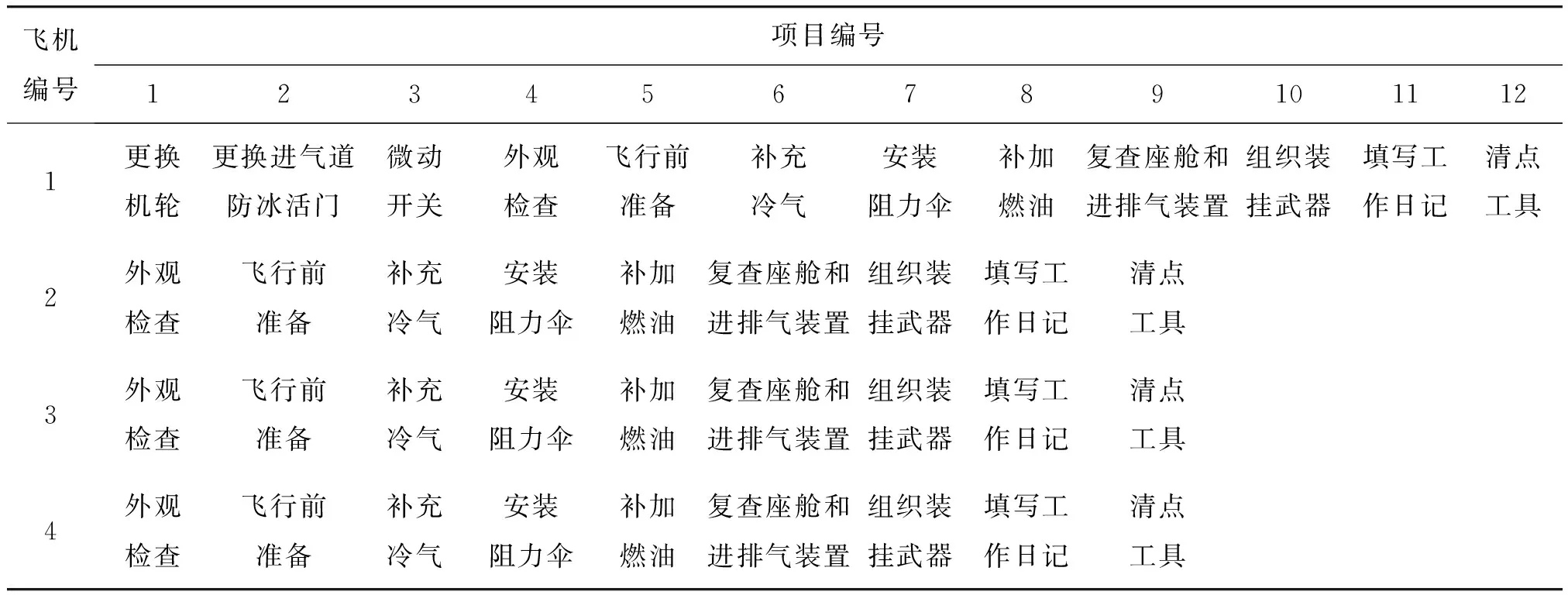
表3 每架飞机需要进行的维修保障项目内容Table 3 Maintenance and support task of aircraft fleet
器挂载工作,飞机2,3和4为完好飞机只进行机务准备和武器挂载工作。可以看出飞机1的维修工作最多且包含了飞机2,3和4的所有工作,其保障时间明显要比飞机2,3和4的持续时间长,采用机组维修的方式,多架飞机同时保障,即4架飞机并行作业,在此以飞机1代替机群为研究对象,建立其随机维修保障网络如图2所示。
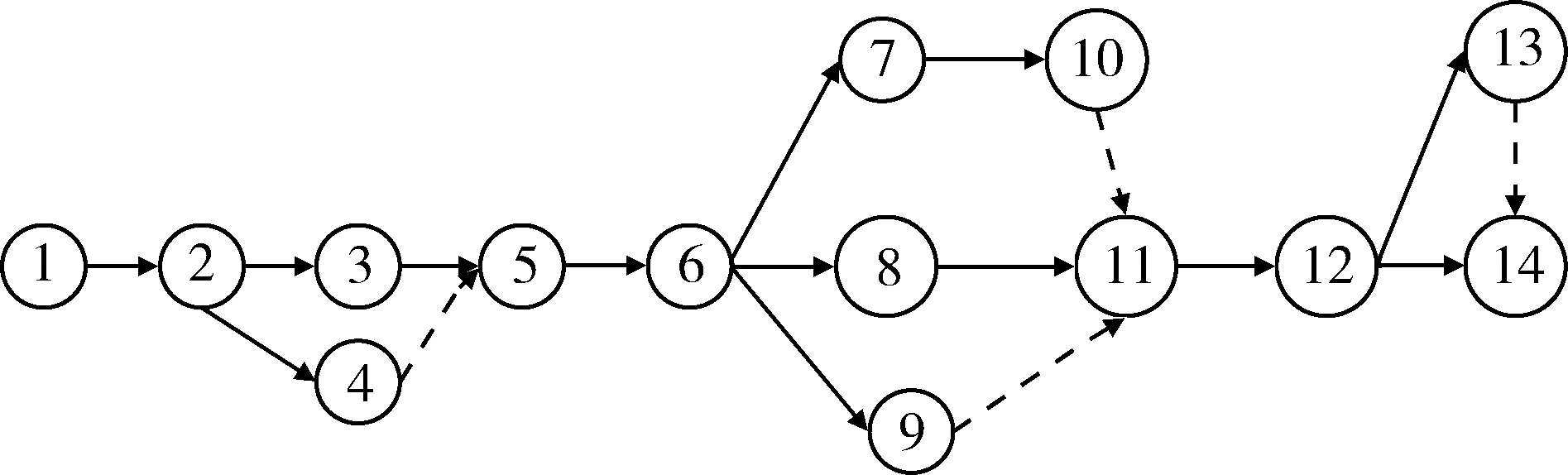
图2 飞机群维修保障网络Fig.2 Maintenance task PERT of aircraft

图2中共有14个节点,12条完整的路径。按照2.2设计方法,采用Matlab 9.0编程,首先通过Monte Carlo仿真,计算出图2中成为关键路径概率最高的路径。其中,路径1-2-3-5-6-8-11-12-14成为关键路径的概率为0.632,是概率最大的,因此作为关键路径。再次使用Monte Carlo对其路径上的工期进行仿真,结果如图3所示。

图3 机群装备战备完好率随工期时间的变化曲线Fig.3 Aircraft fleet operational readiness vs. support time
Monte Carlo仿真曲线表示用蒙特卡罗方法对PERT图中关键路径进行仿真得到的结果;拟合曲线表示假关键路径上工期持续时间服从正态分布拟合出来的曲线。二者共同表明,随着保障时间的增长,机群战备完好率是增加的,保障任务完成的时间分布在62~80 min之内,随着保障时间的增加,保障项目完成的概率增高,到80 min时所有装备保障任务基本完成,装备的战备完好率达到100%。表明在保障任务确定的情况下,保障系统配置不变,随着保障时间增长,装备的可用性提高,同时说明该仿真曲线能有效的表现出装备可用的真实变化过程。
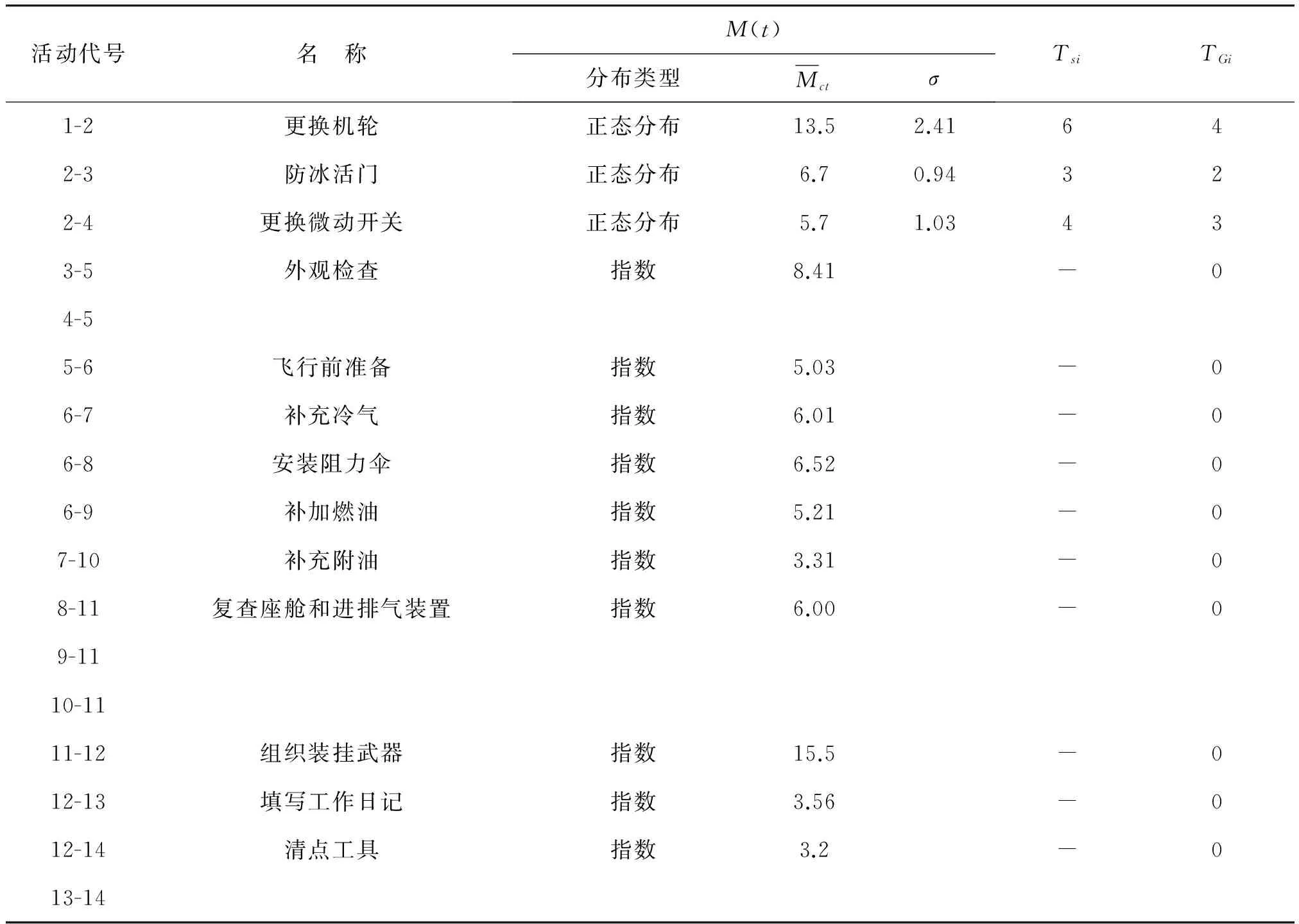
表4 图中节点的分布函数及参数Table 4 Distribution function and parameter of support activities
4 结论
(1) 本文综合考虑机群装备战备完好率建模的各项因素,建立了机群装备战备完好率的仿真模型。以作战任务要求为输入,结合装备的技术状态,根据O&MTA建立维修保障项目的PERT网络,然后确定各节点上的修复时间、备件等待延误时间、资源组等待时间的分布函数及参数,采用蒙特卡罗算法对任务准备期内的维修保障项目工期进行仿真,得出机群装备战备完好率随保障时间的变化曲线,该曲线较为真实地反映了机群装备在任务准备期和任务准备期结束后的可用性,为装备的使用决策提供参考。
(2) 该模型可以度量面向不同作战任务,不同技术状态条件下保障系统的维修保障能力,可以对保障系统的保障效能进行评估。
(3) 该方法可以估算出在不同保障任务和保障资源配置的情况下想达到可用机群数量的所需的保障时间,即任务准备期的时间长短。
(4) 在以后工作中可以进一步分析维修时间、保障延误时间、资源等待时间在战备完好性仿真中的灵敏度,从而对保障系统的资源配置、优化和保障任务调度决策提供指导。
[1] 康锐,王自立.可靠性系统工程的理论与技术框架[J].航空学报,2005,26(5):633-636. KANG Rui,WANG Zi-li.Framework of Theory and Technique about Reliability System Engineering[J].Acta Aeronautica et Astronautica Sinica,2005,26(5):633-636.
[2] 康锐.可靠性维修性保障性工程基础[M].北京:国防工业出版社,2012. KANG Rui.Fundament of Reliability & Maintainability & Supportability[M].Beijing:National Defense Industry Press,2012.
[3] 曲群.如何保证装备的战备完好度[J].现代电子,2000(3):60-62. QU Qun.How to Ensure the Readiness of Armaments[J].Modern Electronics,2000(3):60-62.
[4] RODR IGUES M B,KARPOW ICZ M,KANG K.A Readiness Analysis for the Argentine Air Force and the Brazilian Navy A-4 Fleet Via Consolidated Logistics Support[C] ∥Proceeding of the 2000 Winter Simulation Conference.Orlando:1068-1074.
[5] ESTHER F,BENNY L.On the Availability of R out of N Repairable Systems[J].Naval Research Logistics,2002,49:483-498.
[6] LEVITIN G.The Universal Generating Function in Reliability Analysis and Optimization[M].Springer,2005.
[7] LEWISTP,COCHRAN J K.Applying Queuing Theory to Improve the Modeling of Spares Provisioning of Small Combat Aircraft Units[J].Computers Industry Engineering,1995,29(4):297-301.
[8] COCHRAN J K,LEW IS T P.Computing Small Fleet Aircraft Availabilities Including Redundancy and Spares[J].Computers & Operations Research,2002,29:529-540.
[9] 焦健,王自力.军用飞机使用可用度仿真论证[J].北京航空航天大学报,2006,32(1):112-116. JIAO Jian,WANG Zi-li.Operational Availability Demonstration of Military Airplane Based on Simulation[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(1):112-116.
[10] 张建军,郭波,刘芳,等.任务准备阶段复杂武器系统战备完好率评估模型[J].系统工程与电子技术,2006,28(10):1533-1537. ZHANG Jian-jun,GUO Bo,LIU Fang,et al.Model for Evaluating the Operational Readiness of Complex Weapon System During the Mission Preparation Period[J].Systems Engineering and Electronics,2006,28(10):1533-1537.
[11] 刘芳,赵建印,宋贵宝.任务准备阶段机群战备完好率评估模型[J].哈尔滨工业大学学报,2008,40(3):488-491. LIU Fang,ZHAO Jian-yin,SONG Gui-bao.A Model on Evaluating Operational Readiness of an Air Fleet During Mission Ready Time[J].Journal of Harbin Institute of Technology,2008,40(3):488-491.
[12] 丁定浩,陆军.维修时间新参数和维修性设计技术新进展[J].中国电子科学研究院学报,2010,5(4):301-388. DING Ding-hao,LU Jun.New Parameter of Maintenance Time and New Development in Maintenance Design Technology[J].Journal of CAEIT,2010,5(4):301-388.
[13] 丁定浩,陆军,王斌.新型战备完好率模型[J].电子产品可靠性与环境试验,2010,28(3):1-5. DING Ding-hao,LU Jun,WANG Bin.A Novel Readiness Model[J].Electronic Product Reliability and Environment Testing,2010,28(3):1-5.
[14] 丁定浩.以LRU 的RMS 参数表达的战备完好率模型[J].电子产品可靠性与环境试验,2012,30(1):1-5. DING Ding-hao.Readiness Model Expressed with Parameters of RMS Supportability of LRUs[J].Electronic Product Reliability and Environment Testing,2012,30(1):1-5.
[15] 陈光宇,李婧,刘楠,等.时间约束下k/N(G)机群任务可用度的建模方法[J].电 子 科 技 大 学 学 报,2014,43(6):943-949. CHEN Guang-yu,LI Jing,LIU Nan.Mission Availability Modeling Methods for k/N(G) Fleet under Time Constraints[J].Journal of University of Electronic Science and Technology of China,2014,43(6):943-949.
[16] 岳奎志,侯志强,韩维,等.机群出动能力的Markov模型[J].系统仿真学报,2008,20(22):6278-6281. YUE Kui-zhi,HOU Zhi-qiang,HAN Wei,et al.Markov Model of Air Fleet Sortie Ability[J].Journal of System Simulation,2008,20(22):6278-6281.
[17] 张卓,岳奎志,韩维,等.作战飞机出动能力评估模型[J].海军航空工程学院学报,2007,22(6):659-662. ZHANG Zhuo,YUE Kui-zhi,HAN Wei,et al.Assessment Model of the Military Aircrafts Executing Ability[J].Journal of Naval Aeronautical and Astronautical University,2007,22(6):659-662.
[18] 韩维,李成,商兴华.基于Markov模型的机群完好率研究[J].飞机设计,2011,31(4):60-63. HAN Wei,LI Cheng,SHANG Xing-hua.Study on the Readiness Rate of Air Fleet Based on Markov Model[J].Aircarft Design,2011,31(4):60-63.
[19] WANG Jian,WANG Hong-wei.A CMMS-Based Formal Conceptual Modeling Approach for Team Simulation and Training[J].Lecture Notes in Computer Science,2009(1):946-955.
[20] CJCSM3500.04C.Universal Joint Task List[R].http:∥www.dtic.mil/doctrine/jel/cjcsd/cjcsm/ m350004c.pdf.
[21] 李军亮,滕克难.舰载机作战任务要求到装备保障要求转换研究[J],舰船科学学技术,2016,38(1):150-153. LI Jun-liang,TENG Ke-nan.Rsearch on Transformation from Operation Requirement to Support Requirement of Carrier-Based Aircraft[J].Ship Science and Technology,2016,38(1):150-153.
[22] 徐宗昌.保障性工程[M].北京,兵器工业出版社,2002. XU Zong-chang.Supportability Engineering[M].Beijing:Weapon Industry Press,2002.
[23] 王学望,康锐,张侦英.任务驱动的保障活动时间优化[J].计算机集成制造系统,2010,16(10):2227-2232. WANG Xue-wang,KANG Rui,ZHANG Zhen-ying.Task Driven Support Activity Time Optimization[J].Computer Integrated Manufacturing Systems,2010,16(10):2227-2232.
[24] 郭霖瀚,康锐,文佳.以保障活动为中心的装备保障资源数量预测[J].航空学报,2009,30(5):919-924. GUO Lin-han,KANG Rui,WEN Jia.Quantitative Forecast of Support Activity Centered Equipment Support Resources[J].Acta Aeronautica et Astronautica Sinica,2009,30(5):919-924.
[25] 文佳,康锐.平均维修保障等待时间的计算方法[J].北京航空航天大学学报,2010,36(4):451-454. WEN Jia,KANG Rui.Calculation Methods for Mean Waiting Time of Maintenance Support[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(4):451-454.
Military Aircraft Fleet Operational Readiness Research
LI Jun-liang1,2,TENG Ke-nan1,XU Ji-hui1,XIA Fei3,LI Ji-ying1
(1.Naval Aeronautical Engineering Institute,Shandong Yantai 264000,China;2.PLA,No.92635 Troop,Shandong Qingdao 266041,China;3.State Grid Liaoyang Electric Power Supply Company,Liaoning Liaoyang 111000,China)
In considering of the three relations among mission requirement, aircraft fleet and support system,a mission-driven aircraft fleet operational readiness simulation model is established. Using the operational mission requirements and aircraft fleet technical state as inputs, performing O&MTA,the PERT network with logic certainty and stochastic schedule is set up. The distribution functions and parameters of maintenance time, spare parts delay time and resource group waiting time of the nodes and paths in the PERT network are analyzed. The most critical paths are found by using Monte Carlo method. By calculating the selected critical paths, the change rate of the aircraft fleet readiness rate with the support time can be obtained. The results show that the simulation model can reflect the real situation of aircraft fleet operational readiness rate under different mission requirement and support system, and can provide decision support for equipment operational use.
aircraft fleet;operational readiness;PERT network;Monte Carlo;maintenance;support
2016-05-10;
2016-08-23
李军亮(1982-),男,陕西岐山人。博士生,研究方向为装备保障理论与应用。
10.3969/j.issn.1009-086x.2017.03.024
E926.3;TB114.3
A
1009-086X(2017)-03-0147-08
通信地址:264000 山东省烟台市芝罘区二马路188号海军航空工程学院科研部软件中心
E-mail:Navy_air523@126.com

