改进的防空导弹武器系统作战效能评估模型*

陈金宏，鲁明，黄凯

(海军指挥学院，江苏 南京 210016)

改进的防空导弹武器系统作战效能评估模型*

陈金宏，鲁明，黄凯

(海军指挥学院，江苏 南京 210016)

针对当前防空导弹武器系统作战效能评估模型的局限性，运用排队论基本原理，基于目标有限等待和差错服务，构建了改进的作战效能评估模型，并应用该模型进行了验证计算。结果表明，防空导弹的飞行速度、杀伤区远界和每次射击击毁概率是影响防空导弹武器系统作战效能的主要因素，对于优化防空兵力部署、改进武器系统性能具有一定的参考价值。

防空导弹武器系统；作战效能评估；目标有限等待；差错服务；飞离强度；有效服务强度

0 引言

防空导弹武器系统作战效能分析是合理构建防空体系的重要依据。从排队论的角度看，来袭目标飞越防空导弹武器系统射击服务区(以下简称射击服务区)的过程，相当于有限等待和接受差错服务[1]，若目标成功接受射击服务(被击毁)而消失，视为服务有效，否则目标再次接受射击服务；若目标等待服务或接受服务的时间过长，目标将飞离射击服务区而成功突防。本文基于目标有限等待和差错服务，对所有进入射击服务区的目标计算飞离强度，并以有效服务强度作为系统服务能力指标，改进了防空导弹武器系统的作战效能评估模型。

1 基本假设

(1) 长时间持续来袭的目标流近似于强度为λ的泊松流，即在时间(0，t)内来袭目标数Xt的概率分布为P(Xt=k)=(λt)ke-λt/k! (k=0，1，2，…)。

由于泊松流最难于抗击[2]，将目标流视为泊松流，可以从最困难条件下分析防空导弹武器系统的作战效能。防空导弹武器系统部署于保卫目标旁，来袭目标径直攻击保卫目标，不干扰、抗击或机动规避防空导弹武器系统的拦截。

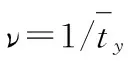
图1 射击服务区与杀伤区的垂直剖面示意图Fig.1 Schematic diagram of vertical section of shoot service zone and kill zone

在上述假设条件下，防空导弹武器系统可视为基于目标有限等待和差错服务的M/M/n：∞/∞/FCFS随机服务系统，即来袭目标流是泊松流，射击时间服从负指数分布，n个服务台，系统容量无限，目标源总量无限，先到先服务。射击服务过程的排队模型如图2所示。

图2 射击服务过程的排队模型Fig.2 Queuing model for shooting service process

2 状态分析

定义t时刻随机服务系统的状态为此时处于射击服务区内目标的随机数量Xt。则服务系统可能处于以下3种状态：

(1)Xt=0，射击服务区内目标数为0，n个火力通道均不射击；

(2)Xt=k(k=1，2，…，n-1)，射击服务区内目标数为k，k个火力通道正在射击；

(3)Xt=n+s(s=0，1，2，…)，射击服务区内目标数为n+s，n个火力通道均在射击，s个目标在等待射击。

由基本假设可知：

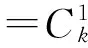
以Pi(t)(i=0，1，…)表示t时刻系统处于状态Xt=i的概率，下面对Pi(t)进行讨论。

(1) 系统处于状态Xt=0时

t+Δt时刻，系统处于状态Xt+Δt=0的概率可表述为下列3个独立事件的概率之和：

1)t时刻，系统处于状态Xt=0，且Δt时间内无新目标进入。该事件概率为P0(t)[1-λΔt+ο(Δt)] =(1-λΔt)P0(t)+ο(Δt)。

2)t时刻，系统处于状态Xt=1，Δt时间内，无新目标进入，分配给目标的火力通道完成射击并击毁目标，且无目标飞离射击服务区。该事件概率为P1(t)[1-λΔt+ο(Δt)][μΔt+ο(Δt)]Pc[1-νΔt+ο(Δt)]=μPcΔtP1(t)+ο(Δt)。

3)t时刻，系统处于状态Xt=1，Δt时间内，无新目标进入，分配给目标的火力通道未完成射击，该目标飞离射击服务区。该事件概率为P1(t)[1-λΔt+ο(Δt)][1-μΔt+ο(Δt)][νΔt+ο(Δt)]=νΔtP1(t)+ο(Δt)。

因此，t+Δt时刻，系统处于状态Xt+Δt=0的概率为P0(t+Δt)=(1-λΔt)P0(t)+(μPc+ν)Δt·P1(t)+ο(Δt)，则[P0(t+Δt)-P0(t)]/Δt=-λP0(t)+(μPc+ν)P1(t)+ο(Δt)/Δt。

(2) 系统处于状态Xt=k(k=1，2，…，n-1)时

t+Δt时刻，系统处于状态Xt+Δt=k的概率可表述为下列5个独立事件的概率之和：

1)t时刻，系统处于状态Xt=k，Δt时间内，无新目标进入，k个火力通道均未完成射击，且k个目标均未飞离射击服务区。该事件概率为Pk(t)[1-λΔt+ο(Δt)][1-kμΔt+ο(Δt)]·[1-kνΔt+ο(Δt)]=[1-(λ+kμ+kν)Δt]·Pk(t)+ο(Δt)。

2)t时刻，系统处于状态Xt=k，Δt时间内，无新目标进入，仅1个火力通道完成射击但未击毁目标，且k个目标均未飞离射击服务区。该事件概率为Pk(t)[1-λΔt+ο(Δt)][kμΔt+ο(Δt)](1-Pc)[1-kνΔt+ο(Δt)]=kμ(1-Pc)ΔtPk(t)+ο(Δt)。

3)t时刻，系统处于状态Xt=k+1，Δt时间内，无新目标进入，仅1个火力通道完成射击并击毁目标，且k+1个目标均未飞离射击服务区。该事件概率为Pk+1(t)[1-λΔt+ο(Δt)][(k+1)μΔt+ο(Δt)]Pc[1-(k+1)νΔt+ο(Δt)]=(k+1)·μPcΔtPk+1(t)+ο(Δt)。

4)t时刻，系统处于状态Xt=k+1，Δt时间内，无新目标进入，k+1个火力通道均未完成射击，仅1个目标飞离射击服务区。该事件概率为Pk+1(t)·[1-λΔt+ο(Δt)][1-(k+1)μΔt+ο(Δt)]·[(k+1)νΔt+ο(Δt)]=(k+1)νΔtPk+1(t)+ο(Δt)。

5)t时刻，系统处于状态Xt=k-1，Δt时间内，仅1个新目标进入，k-1个火力通道均未完成射击，且k-1个目标均未飞离射击服务区。该事件概率为Pk-1(t)[λΔt+ο(Δt)][1-(k-1)μΔt+ο(Δt)][1-(k-1)νΔt+ο(Δt)]=λΔtPk-1(t)+ο(Δt)。

因此，t+Δt时刻，系统处于状态Xt+Δt=k的概率为Pk(t+Δt)=[1-(λ+kμPc+kν)Δt]Pk(t)+[(k+1)(μPc+ν)Δt]Pk+1(t)+λΔtPk-1(t)+ο(Δt)，则[Pk(t+Δt)-Pk(t)]/Δt=-[λ+k(μPc+ν)]Pk(t)+(k+1)(μPc+ν)Pk+1(t)+λPk-1(t)+ο(Δt)/Δt。

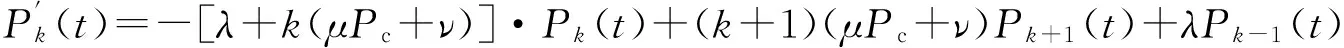
类似可得服务系统状态变化的微分方程组为

(1)

由微分方程组(1)可知，该服务系统状态转移图如图3所示。当系统中目标数为k(k=1，2，…，n-1)时，目标流将受到强度为kμPc的有效射击而损毁，同时将有强度为kν的目标流飞离射击服务区而成功突防；当系统中目标数为n+s(s=0，1，2，…)时，目标流将受到强度为nμPc(已达系统最大有效服务能力)的有效射击而损毁，同时将有强度为(n+s)ν的目标流成功突防。

文献[3-13]中系统状态转移图如图4所示。对比图3、图4可知，本文建立的模型与文献[3-13]存在2个区别：

(1) 文献[3-13]主张未接受射击服务的目标有限等待，对于接受射击服务的目标不考虑飞离强度，一旦服务开始，不管等待时间多长，都将完成射击服务，但实际上可能出现未完成射击服务，目标就已飞离射击服务区的情况。本文基于所有目标有限等待，从状态Xt=0开始引入飞离强度ν，更符合作战过程，因为任一目标飞越射击服务区相当于有限等待，飞越时间达到有限等待时间，该目标都将飞离射击服务区成功突防，而与目标是否接受射击服务无关。

(2) 文献[3-13]以服务强度μ作为系统服务能力指标，计算稳态下未受射击而直接突防的概率Pt和目标受射击概率Ps(Ps=1-Pt)，进而求得目标流击毁概率Ph(Ph=PsPc)，相当于以未受射击而直接突防的目标数推算受射击目标数，以受射击目标数乘以击毁概率Pc计算击毁目标数。通常击毁概率Pc是经大量射击试验后，由击毁目标数除以总射击次数得来。由于实际作战中每个目标对应的射击次数是不定的，以受射击目标数代替总射击次数来计算击毁目标数，将带来一定误差。实际上，射击过程具有差错服务的特点，目标流在受到强度为μ的射击后，平均强度为μPc的目标流被击毁而消失，即单火力通道有效服务强度为μPc，受射击但未被击毁(服务无效)的目标将继续留在队列中再次接受服务，直至被击毁或飞离射击服务区，可一定程度上体现射击次数，以此计算的击毁目标数更为合理。因此，本文基于差错服务，以有效服务强度μPc作为系统服务能力指标，能更真实地反映作战过程。

3 系统性能指标

图3 基于目标有限等待和差错服务的防空导弹武器系统状态转移图Fig.3 State transition diagram of air defense missile weapon system based on target finite waiting and false-serving

图4 文献[3-13]中防空导弹武器系统状态转移图Fig.4 State transition diagram of air defense missile weapon system in the literature [3-13]

(2)

于是得到：

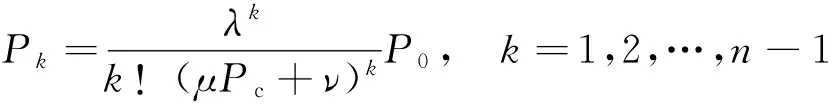
(3)

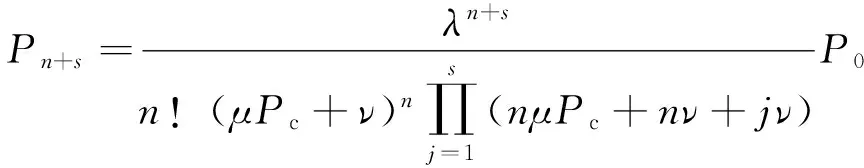
s=0，1，2，….

(4)

(5)

系统主要性能指标如下：

进入防空导弹射击服务区的目标的平均数，即平均队长为

(6)

射击服务区中正受到射击的目标的平均数，即平均服务队长为

(7)

飞离射击服务区前未接受射击服务的目标的平均数，即平均排队长为

(8)

对于射击服务区中每个未接受射击服务的目标都将以强度ν飞离射击服务区，因此目标等待射击服务超时而直接突防的概率为

(9)

对于射击服务区中每个接受射击服务的目标也将以强度ν飞离射击服务区，因此目标接受射击服务超时而突防的概率为

(10)

射击服务区中的所有目标都以强度ν飞离，目标总突防概率为

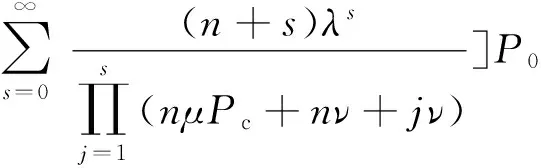
(11)

防空导弹武器系统以强度μPc击毁所射击的目标，目标被击毁概率为

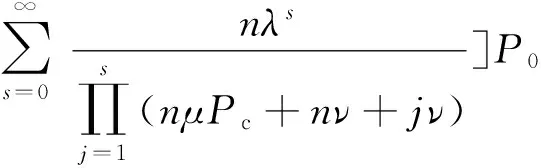
(12)

防空导弹武器系统的作战目的就是最大限度地击毁来袭目标，因此本文以目标被击毁概率Ph作为防空导弹武器系统的作战效能指标。

受到射击的目标中，被击毁的概率为

(13)

图随ν/μ变化的曲线Fig.5 Curves of with ν/μ changes

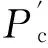
实际防空作战中，还需考虑目标发现概率、指挥概率、引导概率、截获概率、可靠性概率、反干扰概率、反机动概率，可用乘积方式将有效服务强度由μPc修正为μPcx；当目标流中部分目标的突防高度超出武器系统有效抗击范围[15]时，视为未发现目标，可用该比例修正目标发现概率；考虑武器系统(服务台)战损概率，相当于火力通道数n减少。

4 算例分析

假设某防空导弹武器系统装备有8辆垂直发射车，每辆垂直发射车有2个发射通道，即系统火力通道数为16，导弹平均速度vd为1 km/s，射击准备时间tz为8 s，每次射击击毁概率Pc=0.75，目标发现概率等其余概率均假设为1。该防空导弹武器系统部署于保卫目标旁，采用单射方式拦截来袭目标，备弹充足，装填及时。来袭飞机防区外发射巡航导弹或是距保卫目标25 km时发射高速反辐射导弹然后返航。对于速度为300 m/s、高度为25 m超低空突防的来袭飞机，由于杀伤区远界过近，无法抗击，而只能拦截其发射的导弹。防空导弹武器系统假想参数如表1所示。

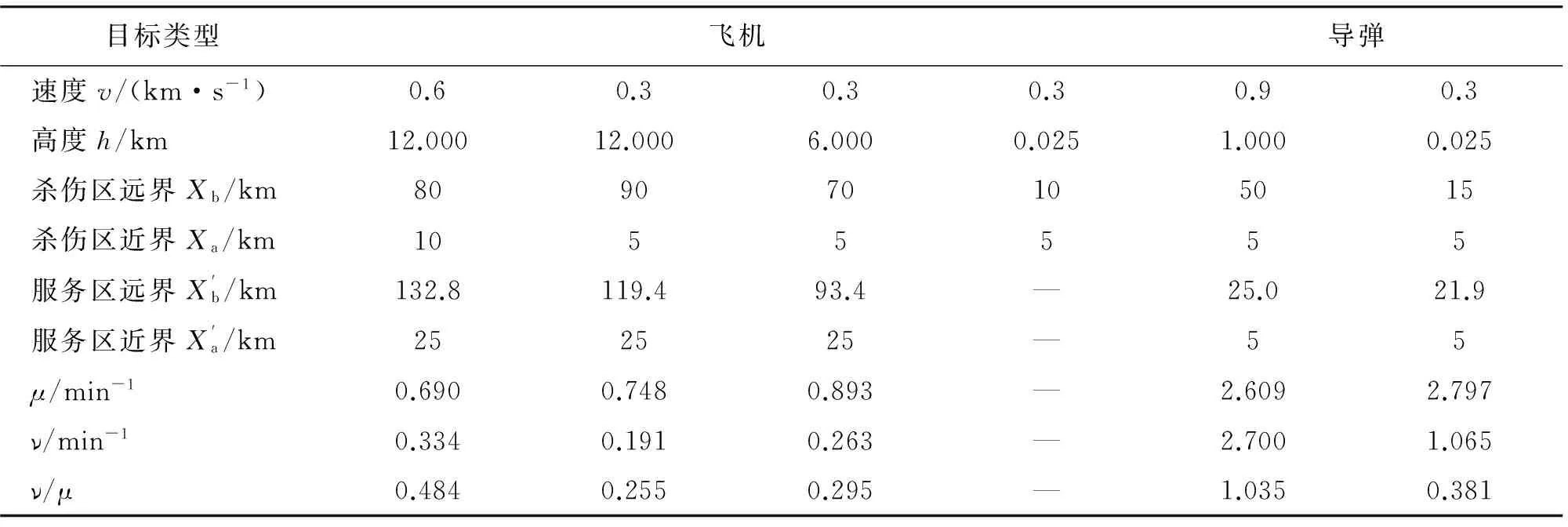
表1 防空导弹武器系统假想参数Table 1 Hypotheticalparametersof air defense missile weapon system

(14)

(15)

(16)

根据式(5)，(12)，可求得不同目标流强度下的目标被击毁概率Ph，并以此作为防空导弹武器系统的作战效能指标。计算结果如表2所示。

由式(13)整理可得

(17)

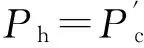
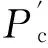
从以上曲线可以判断：提高防空导弹飞行速度vd和每次射击击毁概率Pc，延伸防空导弹杀伤区远界Xb，均可大幅提升防空导弹武器系统的作战效能，但提升幅度逐渐趋缓，进一步提高参数，收效不明显；缩短射击准备时间tz，对抗击导弹目标意义较大，但对抗击飞机目标效果并不明显。

图 随vd变化的曲线Fig.

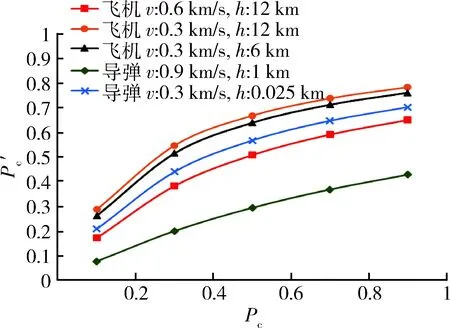
图 随Pc变化的曲线Fig.7 Curves of with Pc changes

目标飞机导弹v:0.6km/sh:12kmv:0.3km/sh:12kmv:0.3km/sh:6kmv:0.9km/sh:1kmv:0.3km/sh:0.025kmλ/min-120.6080.7460.7180.4200.66340.6080.7460.7180.4200.66380.6070.7420.7170.4200.663160.5080.5390.6270.4200.663320.2590.2700.3200.4200.661640.1290.1350.1600.3940.5221280.0650.0670.0800.2340.262P'c0.6080.7460.7180.4200.663

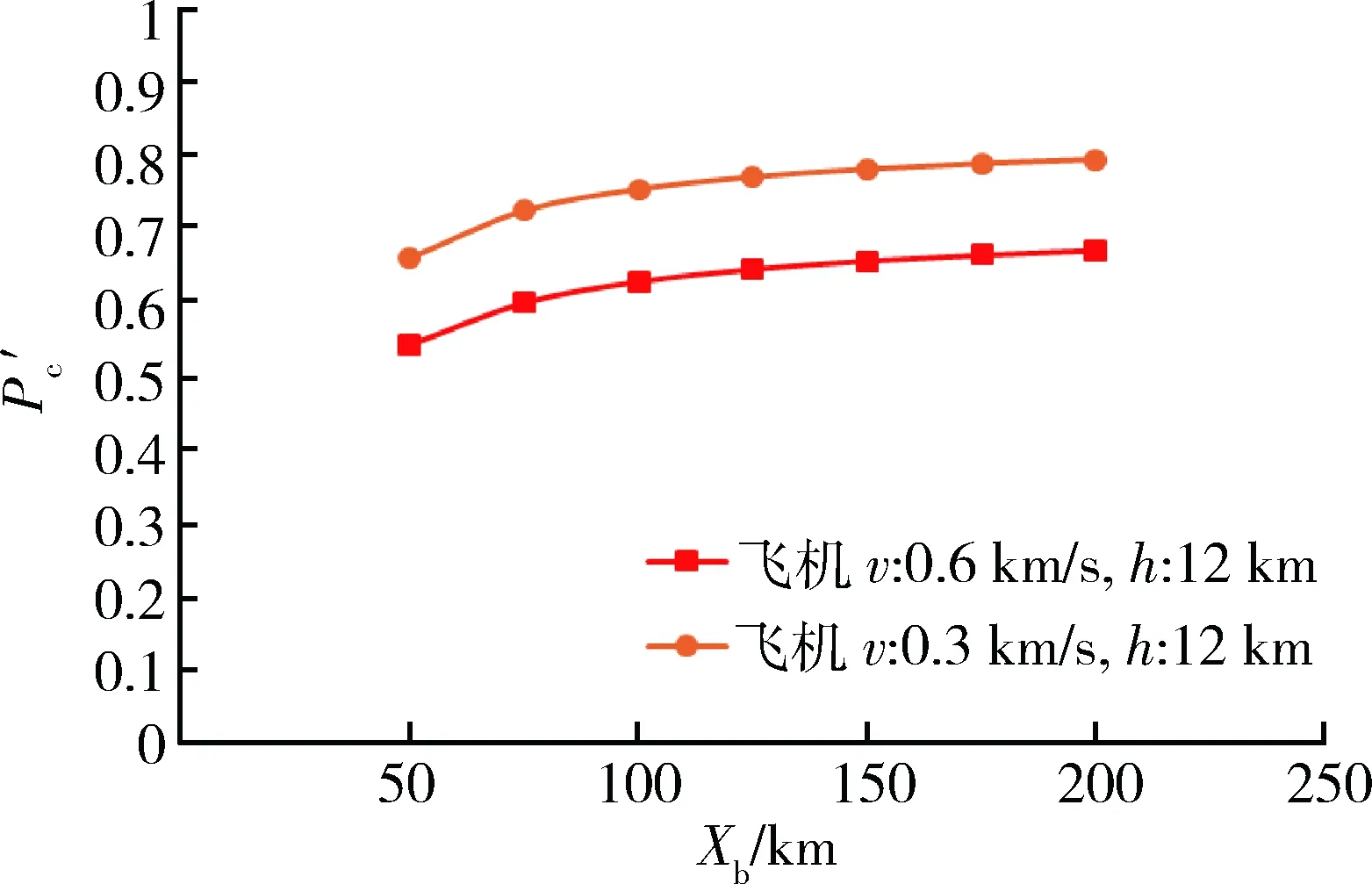
图 随Xb变化的曲线Fig.8 Curves of with Xb changes

图 随tz变化的曲线Fig.9 Curves of with tz changes

5 结束语

本文针对当前防空导弹武器系统作战效能评估模型的局限性，运用排队论基本原理，基于目标有限等待和差错服务，构建了改进的作战效能评估模型，并应用该模型进行了验证计算。结果表明，防空导弹的飞行速度、杀伤区远界和每次射击击毁概率是影响防空导弹武器系统作战效能的主要因素。为达到预期的防空作战效能指标，应针对这三个主要因素，优选防空导弹武器系统或改进现有的防空导弹武器系统性能，并以此作为构建防空体系、优化防空部署的重要依据。

[1] 龙光正，严国顺，龙晓伟.基于SPN有限等待差错服务的火力单元排队模型[J].火力与指挥控制，2004，29(6)：26-28. LONG Guang-zheng，YAN Guo-shun，LONG Xiao-wei.Firepower Unit Finite Waiting False-Serving Queue Model Based on SPN [J].Fire Control & Command Control，2004，29(6)：26-28.

[2] 史越东.军事运筹学教程[M].南京：海军指挥学院，2010：152-166. SHI Yue-dong.Military Operational Research Course [M].Nanjing：Naval Command College，2010：152-166.

[3] 韩松臣.导弹武器系统效能分析的随机理论方法[M].北京：国防工业出版社，2001：61-67. HAN Song-chen.Stochastic Theory and Method for Effectiveness Analysis of Missile Weapon Systems [M].Beijing：National Defense Industry Press，2001：61-67.

[4] 张明智，娄寿春，聂成.海上防空模型研究[J].系统工程理论与实践，2001(8)：111-118. ZHANG Ming-zhi，LOU Shou-chun，NIE Cheng.The Study of Maritime Air Defense Model [J].Systems Engineering-Theory & Practice，2001(8)：111-118.

[5] 苑立伟，杨建军，张多林.基于排队论的防空导弹群作战效能研究[J].现代防御技术，2005，33(5)：4-7. YUAN Li-wei，YANG Jian-jun，ZHANG Duo-lin.Research on Operational Efficiency of Air Defense Missile Group Based on Queuing Theory [J].Modern Defense Technology，2005，33(5)：4-7.

[6] 俄罗斯朱可夫防空军事指挥学院.防空作战模拟与效能评估[M].来斌，牛存良，熊友奇，译.北京：军事科学出版社，2005：18-22. Zhukov Air Defense Military Command College of Russia.Air Defense Combat Simulation and Performance Evaluation [M].LAI Bin，NIU Cun-liang，XIONG You-qi，Translated.Beijing：Military Science Press，2005：18-22.

[7] 陈立新，殷兴良，陈万春.采用随机服务系统理论分析网络中心化防空作战[J].系统仿真学报，2005，17(7)：1670-1673. CHEN Li-xin，YIN Xing-liang，CHEN Wan-chun.Analysis of Network Centric Air Defense Operation Using Stochastic Service System Theory [J].Journal of System Simulation，2005，17(7)：1670-1673.

[8] 苑立伟，杨建军，赵保军，等.防空导弹群作战效能中拦截适宜性因子的确定[J].战术导弹技术，2006(3)：44-47. YUAN Li-wei，YANG Jian-jun，ZHAO Bao-jun，et al.The Determination of Interception Fitness Factor in Research on Operational Effectiveness of Air Defense Missile Group [J].Tactical Missile Technology，2006(3)：44-47.

[9] 刘钢，徐清华，周智超，等.基于排队论的反舰导弹突防概率研究[J].火力与指挥控制，2008，33(12)：102-105. LIU Gang，XU Qing-hua，ZHOU Zhi-chao，et al.Study on Penetration Probability of Anti-Ship Missile Based on Queuing Theory [J].Fire Control & Command Control，2008，33(12)：102-105.

[10] 贺川，王桂花，蒋里强，等.基于排队论的地空导弹武器系统作战效能评估[J].火力与指挥控制，2010，35(5)：110-113. HE Chuan，WANG Gui-hua，JIANG Li-qiang，et al.The Operational Effectiveness Assessment of the Surface-to-air Missile Weapon System Based on Queuing Theory [J].Fire Control & Command Control，2010，35(5)：110-113.

[11] 彭绍雄，李学园，邹强，等.基于排队论的舰空导弹武器系统射击效能研究[J].战术导弹技术，2011(4)：5-7. PENG Shao-xiong，LI Xue-yuan，ZOU Qiang，et al.Research on Anti-Missile Firing Effectiveness of Ship-to-Air Missile System Based on Queuing Theory [J].Tactical Missile Technology，2011(4)：5-7.

[12] 李仁松，姜志刚，赵磊.多目标通道的舰空导弹武器系统作战效能评估[J].舰船电子工程，2011，31(9)：27-30. LI Ren-song，JIANG Zhi-gang，ZHAO Lei.Efficiency Evaluation of the Ship’s Multi-Targeting Ship-to-Air Missile Defense System [J].Ship Electronic Engineering，2011，31(9)：27-30.

[13] 赵广彤，俞一鸣，刘群，等.基于排队论的防空导弹武器系统作战效能研究[J].现代防御技术，2014，42(1)：19-24. ZHAO Guang-tong，YU Yi-ming，LIU Qun，et al.Research on Combat Effectiveness of Antiaircraft Missile Weapon System Based on Queuing Theory [J].Modern Defense Technology，2014，42(1)：19-24.

[14] CHUNG K L.Markov Chain with Stationary Transition Probabilities [M].Berlin：Springer，1985.

[15] 朱雪平，李东伟，王敬华.基于排队论的地面防空系统服务概率研究[J].指挥控制与仿真，2013，35(1)：71-73. ZHU Xue-ping，LI Dong-wei，WANG Jing-hua.Research on the Service Probability of the Ground Air Defense System Based on Queuing Theory [J].Command Control & Simulation，2013，35(1)：71-73.

Improved Model for Operational Effectiveness Assessment of Air Defense Missile Weapon System

CHEN Jin-hong，LU Ming，HUANG Kai

(Naval Command College，Jiangsu Nanjing 210016，China)

Aiming at the current limit in assessing operational effectiveness of air defense missile weapon system, applying basic principle of queuing theory, and based on target finite waiting and false-serving, an improved model is established for operational effectiveness assessment. The verifying results show that flight speed, kill zone boundary and destruction probability of air defense missile are major factors affecting the operational effectiveness of air defense missile weapon system．This assessment model can provide reference value in optimizing disposition of air defense troops and improving performance of weapon system.

air defense missile weapon system；operational effectiveness assessment；target finite waiting；failed serving；flying away intensity；effective service intensity

2016-07-20；

2016-09-06

陈金宏(1985-),男,福建福州人。博士生,主要研究方向为海军战术应用理论。

通信地址：210016 江苏省南京市玄武区半山园21号研究生2队 E-mail：cjh5666083@163.com

10.3969/j.issn.1009-086x.2017.03.003

TJ761.1；E844

A

1009-086X(2017)-03-0013-09