冲击噪声环境中波束域DOA估计方法研究*

李洪升，张瑞丰，杜宇，王永孝

(1.中国人民解放军95861部队，甘肃 酒泉 735018；2.中国人民解放军95948部队，甘肃 酒泉 732750)

冲击噪声环境中波束域DOA估计方法研究*

李洪升1，张瑞丰1，杜宇1，王永孝2

(1.中国人民解放军95861部队，甘肃 酒泉 735018；2.中国人民解放军95948部队，甘肃 酒泉 732750)

研究了冲击噪声环境中波束域波达方向(direction of arrival，DOA)估计问题。在冲击噪声环境下，基于共变和分数低阶矩的 ROC-MUSIC和FLOM-MUSIC方法稳健性较差。为了改进空间谱估计性能，首次将波束空间处理应用于共变系数矩阵和分数低阶矩矩阵中，定义了新的波束域共变系数矩阵和波束域分数低阶矩矩阵，提出了新的波束域ROC-MUSIC(BROC-MUSIC)算法和波束域FLOM-MUSIC(BFLOM-MUSIC)算法。理论分析表明，可以通过波束域共变系数矩阵和波束域分数低阶矩矩阵的特征分解来估计噪声子空间，从而实现对信源的DOA估计。计算机仿真结果证明了算法的有效性和正确性。

波束空间；DOA估计；共变矩阵；分数低阶矩；冲击噪声；特征分解

0 引言

冲击噪声背景下波达方向(direction of arrival，DOA)估计问题，近几年得到了国内外学者的广泛重视，已成为空间谱估计的一个新的发展方向，其研究领域已经拓展到雷达、通信、电子对抗及射电天文等许多领域[1-7]。由于在实际应用中，所遇到的许多随机信号和噪声并不是高斯分布的，例如大气雷电噪声、通信线路上的瞬间尖峰语音信号和海洋环境噪声以及多种人为噪声等，这些信号中存在显著的尖峰，用传统的基于二阶统计量的方法进行处理不能得到满意的结果。有一种很重要的统计信号模型称为α稳定分布(Alpha-stable distribution)，可以用来描述上面提到的这类非高斯脉冲信号和噪声[1-2]。然而，稳定分布没有有限的二阶矩，基于二阶统计量的DOA估计方法性能退化较大，不再适用。因此，在MUSIC(multiple signal classification)算法的基础上，文献[3]提出了基于稳健共变的MUSIC(robust covariation-based MUSIC，ROC-MUSIC)方法；文献[4]提出了基于分数低阶矩(fractional lower order moment，FLOM)的MUSIC(FLOM-MUSIC)方法。这2种算法属于阵元域的子空间类算法，需要计算接收数据共变或分数低阶矩矩阵的特征分解，算法计算量较大，且对系统误差较为敏感，稳健性不强。而在高斯噪声假设下，文献[8]提出了基于波束域的MUSIC方法，较好地提高了MUSIC算法的性能。随后，子空间思想[9]和波束域方法[10-13]得到了广泛应用。针对冲击噪声背景下空间谱估计问题，曾在阵元域提出几种新的DOA估计方法[14-15]。在文献[14]中将空间平滑思想引入到了冲击噪声环境中，提出了新的解相干源算法，但稳健性不强。在文献[15]中引入对角加载思想，改进了ROC-MUSIC方法，但也只限于在阵元域中应用，没有提高计算效率。为进一步提高算法的稳健性，在文献[8]启发下，通过构建新的共变系数矩阵和分数低阶矩矩阵，提出了2种新的适用于冲击噪声环境的波束域DOA估计算法。理论分析表明，新算法降低了对系统误差和噪声的敏感性，计算机仿真实验进一步证明了新算法的正确性和稳健性。

1 问题描述及信号模型

假设有D个信号sq(t)入射到由M个阵元组成的一个均匀线阵上，加性噪声nm(t)为复SαS随机变量，1<α≤2。阵列第m个阵元上接收的信号rm(t)可表示为

(1)

式中：am(θq)为信号sq(t)在波达方向θq上第m个阵元的增益，q=1，2，…，D；m=1，2，…，M。

式(1)写成矩阵形式为

(2)

式中：

(3)

(4)

(5)

(6)

若用a(θq)表示来自发射源q 的波阵面的M×1维调整向量：

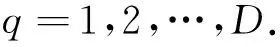
(7)

根据共变的定义[3]，可得入射信号的共变矩阵如下：

(8)

式中：Γs=diag(γs1，γs2，…，γsD)；γsq=(sq，sq)α为信号sq的分散系数(即为信号功率的2倍)；Γn=γnI，(ni(t)，nj(t))α=γnδi，j。

由于

(9)

式中：i，j=1，2，…，M。

则可得

(10)

则ROC-MUSIC算法获得的空间谱[3]为

(11)

另一方面，接收数据的分数低阶矩矩阵为一个M×M维矩阵Cr，其第(i，k)个元素Cik定义为

(12)

可得

(13)

式中：Λ为信号的分数低阶相关矩阵；Cn=γnI。

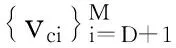
则FLOM-MUSIC算法获得的空间谱[4]为

(14)

2 2种新的波束域DOA估计算法

为了减小计算的复杂性，降低对系统误差的敏感性，提高算法的稳健性，把阵元空间的ROC-MUSIC算法和FLOM-MUSIC算法推广到波束空间，提出了波束空间ROC-MUSIC算法和波束空间FLOM-MUSIC算法，即BROC-MUSIC(beamspace-based ROC-MUSIC)和BFLOM-MUSIC(beamspace-based FLOM-MUSIC)算法。波束域DOA估计原理见图1。

图1 波束域DOA估计Fig.1 Beamspace DOA estimation

考虑阵元间距为半波长的均匀线阵，则阵列的导向向量

(15)

设阵列的接收数据形成B个波束，则这B个波束的归一化加权矩阵为

(16)

通过波束空间变换后的输出

(17)

为B×1维向量，对应的波束空间共变矩阵定义为

Γyy=THΓrT=

TH(AΓsAH+Γn)T=

THAΓsAHT+γnI=

BΓsBH+γnI，

(18)

式中：

B= THA=

THa(θ1)THa(θ2)…THa(θD)=

b(θ1)b(θ2)…b(θD)，

(19)

对(18)式进行特征分解得到

(20)

式中：

Λs=diag(ξ1，ξ2，…，ξD)；

ΛΓ=diag(ξD+1，ξD+2，…，ξB)，

ξi(i=1，2，…，B)为特征值。

Γs=(e1，e2，…，eD)和vΓ=(eD+1，eD+2，…，eB)分别为信号子空间与噪声子空间。

(21)

同理，定义波束空间分数低阶矩矩阵为

Cyy=THCrT=

TH(ACsAH+Γn)T=

THACsAHT+γnI=

BCsBH+γnI.

(22)

(23)

3 仿真计算与结果分析

在下面的仿真实验中，采用8元均匀直线阵，阵元间距为半波长。信源处于远场，冲击噪声满足SαS分布条件且α=1.6。预形成波束数取5。因为α稳定分布噪声不存在有限的二阶矩(即方差不存在)，因此就不能采用一般的信噪比定义(信号与噪声功率比的分贝数)进行性能分析。为了方便合理地考查系统性能，定义广义信噪比为

(24)

假设在冲击噪声背景下，2个不相关信源，其入射方向分别为10°和40°。快拍数为128，分数低阶矩参数p为1.2。200次独立实验，图2给出了4种算法估计的均方误差(MSE)随广义信噪比变化曲线。图3给出了4种算法成功概率随广义信噪比变化的曲线。

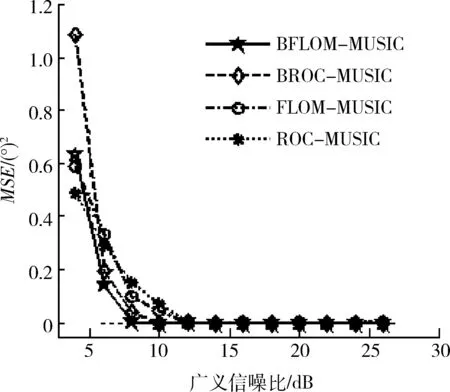
图2 均方误差随广义信噪比变化曲线Fig.2 Change curve of MSE vs. GSNR

图3 成功概率随广义信噪比变化曲线Fig.3 Change curve of success probability vs. GSNR

由图2和图3可知，在广义信噪比小于15 dB情况下，BFLOM-MUSIC和BROC-MUSIC算法总体性能要优于FLOM-MUSIC和ROC-MUSIC算法的。而当广义信噪比超过20 dB时，4种算法的性能相当，都能达到较高的估计精度，估计的成功概率已经接近100%了。

图4表示GSNR为10 dB，快拍数为128时，独立运算20次获得的空间谱曲线图。从图中可以看出，尽管4种算法都能正确分辨出2个信源的波达方向，但以我们提出的BFLOM-MUSIC和BROC-MUSIC算法分辨力最强，而FLOM-MUSIC和ROC-MUSIC算法获得的空间谱具有较高的副瓣。

图4 空间谱Fig.4 Spatial spectra

4 结束语

在雷达和通信信号传输过程，背景噪声和干扰常常表现为非高斯脉冲特性，使得在冲击噪声背景下的空间谱估计问题成为又一个新的研究方向。本文针对这一新问题，提出了2种适用于冲击噪声环境的DOA估计算法。算法引入波束空间的思想，重新构建了共变系数矩阵和分数低阶矩矩阵，并结合子空间算法完成了空间谱估计。仿真实验表明，在低广义信噪比下，BFLOM-MUSIC和BROC-MUSIC算法能克服强噪声干扰，可实现DOA的精确估计，表现出较强的稳健性，且算法在波束域完成，计算量与FLOM-MUSIC算法和ROC-MUSIC算法相比显著降低。

[1] SHAO M，NIKIAS C L.Signal Processing with Fractional Lower Order Moments：Stable Processes and Their Applications[J].Proceedings of IEEE，1993，81(7)：986-1010.

[2] NIKIAS CL，SHAO M.Signal Processing with Alpha-Stable Distributions and Applications[M].New York：John Wiley & Sons Inc.，1995.

[3] ZTSAKALIDES P，NIKIAS C L.The Robust Covariation-Based MUSIC(ROC-MUSIC) Algorithm for Bearing Estimation in Impulsive Noise Environments[J].IEEE Trans.on Signal Processing，1996，44：149-159.

[4] LIU T H，MENDEL J M.A Subspace-Based Direction Finding Algorithm Using Fractional Lower Order Statistics[J].IEEE Trans.on Signal Processing，2001，49：1605-1613.

[5] TSIHRINTZIS G A，NIKIAS C L.Evaluation of Fractional，Lower-Order Statistics-Based Detection Algorithms on Real Radar Sea-Clutter Data[J].Radar，Sonar and Navigation，IEE Proceedings，1997，144(1)：29-38.

[6] SPASOJEVIC P，WANG Xiao-dong.Multi-User Detection in Alpha Stable Noise[J].Military Communications Conference，2001.MILCOM 2001.Communications for Network-Centric Operations：Creating the Information Force.IEEE，2001，2(10)：1087-1090.

[7] 王永孝，李洪升，杨争.冲击噪声背景下引信目标方位估计方法研究[J].现代防御技术，2011，39(4)：80-83. WANG Yong-xiao，LI Hong-sheng，YANG Zheng.Research on DOA Estimation Method for Fuse in Impulse Noise[J].Modern Defence Technology，2011，39(4)：80-83.

[8] STOICS P，NEHORAI A.Comparative Performance Study of Element-Space and Beam-Space MUSIC Estimator E[J].Circuits，Systems，Signal Processing，1991，10(3)：285-291.

[9] VIBERG M，OTTERSTEN B.Sensor Array Processing Based on Subspace Fitting[J].IEEE Trans.on Signal Processing，1991，39(5)：1110-1121.

[10] LINEBARGER D A，DEGROAT R D，DOWLING E M，et al.Constrained Beamspace MUSIC[J].Acoustics，Speech，and Signal Processing，ICASSP-93.，1993，4(4)：27-30.

[11] ZOLTOWSKI M D，SILVERSTEIN S D，MATHEWS C P.Beamspace Root-MUSIC for Minimum Redundancy Linear Arrays[J].Signal Processing，IEEE Transactions on See also Acoustics，Speech，and Signal Processing，IEEE Transactions on，1993，41(7)：2502-2507.

[12] KAUTZ G M，ZOLTOWSKI M D.Beamspace DOA Estimation Featuring Multirate Eigenvector Processing[J].Signal Processing，IEEE Transactions on See also Acoustics，Speech，and Signal Processing，IEEE Transactions on，1996，44(7)：1765-1778.

[13] 洪振清，张剑云.基于波束域预处理的MIMO雷达MVDR波束形成算法[J].系统仿真学报，2013，25(4)：722-727. HONG Zhen-qing，ZHANG Jian-yun.MVDR Beamforming Algorithms Based on Beamspace Processing for MIMO Radar[J].Journal of System Simulation，2013，25(4)：722-727.

[14] 李洪升，杨日杰，何友，等.冲击噪声背景下相干信源DOA估计方法研究[J].微波学报，2008，24(3)：82-86. LI Hong-sheng，YANG Ri-jie，HE You，et al.Research on DOA Estimation Methods of Coherent Sources in the Presence of Impulsive Noise[J].Journal of Microwaves，2008，24(3)：82-86.

[15] 李洪升，孙勇，张瑞峰，等.一种冲击噪声背景下稳健的目标方位估计方法[J].无线电通信技术，2014，40(5)：76-78. LI Hong-sheng，SUN Yong，ZHANG Rui-feng，et al.A Robust DOA Estimation Method for Target in Impulse Noise[J].Radio Communication Technology，2014，40(5)：76-78.

DOA Estimation Method of the Beamspace in Impulsive Noise Environment

LI Hong-sheng1，ZHANG Rui-feng1，DU Yu1，WANG Yong-xiao2

(1.PLA，No.95861 Troop，Gansu Jiuquan 735018，China;2.PLA，No.95948 Troop，Gansu Jiuquan 732750，China )

The estimation of beamspace direction of arrival (DOA) in the impulse noise environment is studied.In the presence of impulsive noise, ROC-MUSIC and FLOM-MUSIC methods based on covariance and fractional lower order moment have poor stability.In order to improve the performance of spatial spectrum estimation, the beamspace processing is applied to covariance coefficient matrix and fractional lower order moments matrix, and new definitions for beamspace covariance coefficient matrix and beamspace fractional lower order moments matrix are made, and new beamspace ROC-MUSIC (BROC-MUSIC) algorithm and beamspace FLOM-MUSIC (BFLOM-MUSIC) algorithm are proposed. The theoretical analysis shows that the noise subspace can be estimated by the characteristics of the beamspace covariance coefficient matrix and beamspace fractional lower order moments matrix decomposition, thus the DOA estimation of source is realized. Computer simulation results show the effectiveness and correctness of the proposed algorithm.

beamspace；direction of arrival(DOA) estimation；covariation matrix；fractional lower order moment；impulsive noise；eigen decomposition

2016-08-25；

2016-09-02

李洪升(1968-)，男，辽宁锦州人。高工，博士后，主要研究方向为信号信息处理。

10.3969/j.issn.1009-086x.2017.03.015

TJ765.3；TP391.9

A

1009-086X(2017)-03-0093-05

通信地址：735018 甘肃省酒泉市14支局844信箱