摭谈一道平面几何题的解法探究与启示

☉江苏泰州市孔桥初级中学 严亚琴

摭谈一道平面几何题的解法探究与启示

☉江苏泰州市孔桥初级中学 严亚琴

平面几何是初中数学课程教学的重要内容之一，几何图形翻折问题是几何学习的重点和难点.由于这类问题要求学生具有一定的综合分析能力，因而受到命题者的青睐.笔者在数学教学中，曾经遇见一道典型的图形翻折问题，学生独立处理的正确率很低.本文对此题进行深入思考与分析，呈现三种解题方法的探究过程，希望能给读者带来一定的参考价值.

一、案例呈现与分析

案例：在△ABC中，∠A=θ，AB=k，P为AC的中点，沿着直线BP将△ABP进行翻折，A点变为A′，满足∠A′CB=θ，则BC=______.

分析：本题主要考查图形翻折问题，题设内容言简意赅，对学生的解题而言存在一定的难度，主要体现在：题目设计图形翻折问题但是没有提供现成的几何图形，要求学生根据题设信息准确作出图形；借助于题设信息分析问题时，需要添加合理的辅助线；需要观察与分析基本几何图形组合与分离的思维能力.在此，笔者对解题思路与方法进行探究，展示三种具体方法的探究过程，供参考.

二、解法探究与启示

解法探究1——“四点共圆”尽显奇妙.

根据题意，构建图形（如图1），连接A′C、AA′、A′B，由于翻折过程中存在对称性特征，所以PA′=PA.

在△AA′C中，PC=PA=PA′，则△AA′C为直角三角形

图1

由于∠PAB=∠PA′B=θ，则∠A′CB=∠ACB+∠PCA′.又∠PA′C=∠PCA′，则∠AA′B=∠ACB，则A′、C、B、A四点共圆.

在Rt△ABC中，根据三角关系可得：BC=AB·tanθ= ktanθ.

启示：本题借助于“四点共圆”的数学规律进行解题，解题过程简洁、利落，解法可谓“精妙”.多数学生难以真正理解这种解法，对灵活运用“四点共圆”处理实际问题更是渺茫，主要原因是中考数学考试说明中没有明确要求学生必须掌握“四点共圆”的数学知识与规律.作为数学教师，在完成圆的基本知识教学后，应该适当补充“四点共圆”的判断与性质，在学生的能力范围内，让学生多掌握一种解决问题的途径与手段.

解法探究2——“补全”图形，活用相似.

根据题意，构建图形（如图2），连接A′C、AA′、A′B，延长AA′和BC相交于Q，借助于解法1中的方法可得到：∠AA′B=∠ACB，则∠QA′B=∠QCA（补角相等）.由于在△QA′B和△QCA中两个对应的角相等，所以△QA′B∽△QCA，则，即

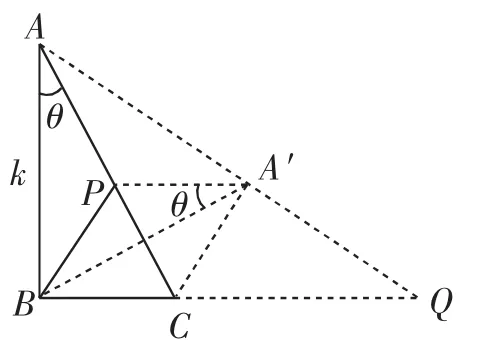
图2

在△QA′C和△QBA中，满足“两边对应成比例且夹角相等”，则△QA′C∽△QBA，则

由三角关系，得BC=AB·tanθ=ktanθ.

启示：此解法是借助于“补全”图形，构造相似三角形来处理问题；其中两对相似三角形的显现得益于“两高”型基本图形的运用，如图4为“两高”型基本图形（AD⊥BQ、 BE⊥AQ），借助于直角三角形相似的性质可以得出，则△QDE∽△QAB.针对这种基本图形特征进行联想与迁移，我们容易在图3中得出：△QA′C∽△QBA.可见，一线数学教师在教学中要注重学生联想与迁移能力的培养.

?

图4

解法探究3——“咬定青山，拨云见日”.

根据题意，构建图形（如图5），延长BP交AA′与M点，连接A′C、AA′、A′B，过C点作CD⊥BP交BP于E点，交AB于D点，结合图形翻折的特征，可得A′M=AM，∠A′MP=，则四边形A′MEC为矩形.由于，则∠BCD=θ.此时可以分离出基本图形（如图6），根据△CBD∽△ABC，可知，即BC2=BD·BA.

图5

图6

启示：此解法是根据题设中已知信息进行探索，基于“共边共角”型基本图形的特征，在原图中构建且分离出基本图形，从而得出重要关系式：BC2=BD·BA，此时可以发现BC为所求量未知，BA=k为已知，BD为未知量且难以求出，部分学生遇到这种情况时容易产生放弃继续探索下去的念头.数学教师在数学解题教学中应该倡导学生保持“咬定青山不放松”的探索精神，树立“条条大道通罗马”的必胜信念，坚信“拨得云开见日出”的必然结果；让学生明白在数学解题中注重基本图形（共边共角）的构建与利用是解决数学难题的一种重要手段.

关于“共边共角”型基本图形的运用，在此我们可以再运用一个案例进行说明，具体如下.

在直角梯形ABCD中，AB∥DC，AD=15，AB=16，BC=12，如图7所示，E、F分别是AB和DC上的动点且F不与点C和D重合，AF与DE相交于G且满足∠AGE=∠DAB，若AE=x，DF=y，试求y关于x的函数表达式（注明x的取值范围）.

剖析：根据题设已知条件，可知在△EGA和△EAD中存在两个对应角相等，则△EGA∽△EAD，则∠ADE=∠GAE=∠AFD.容易发现在△ADF中存在“共边共角”型基本图形，则可得出AD2=AG·AF.

图7

根据题设条件，结合几何关系，可得：DC=7，AF2=（9+y）2+122，则则

三、总结反思与感悟

在初中数学教学中，解题教学是课程教学中的重点，主要目的在于如何想方设法提高学生运用数学知识与规律解决实际问题的能力.在本文中笔者以一道典型的图形翻折问题为探讨基础，列举三种解题方法的探究过程和解题后的想法与启示，由于笔者水平有限和时间仓促，在此问题的处理方法上可能还存在更好的解法与技巧，有待于读者进一步深入探究与思考.当然，我们在实际数学课堂教学中，介绍给学生的解题方法往往都是以“易接受、最优化”为原则.笔者认为在时间允许的情况下，应该引导学生进行一题多解的探究与追求，简洁解法和繁杂解法能够体现数学不同角度的“美景”，学生都能从中得到一定的启发，对于学生综合能力的培养有着重要的促进作用.