在发现式教学中培养数学发散思维

☉广东深圳市龙华区大浪实验学校 王振鑫

☉广东深圳市民治中学 余 涛

在发现式教学中培养数学发散思维

☉广东深圳市龙华区大浪实验学校 王振鑫

☉广东深圳市民治中学 余 涛

当前，数学教学改革和发展的总趋势就是发展思维，培养能力.新课程改革就是要培养学生的发散思维能力.要达到这一要求，教师的教学就必须从优化学生的思维品质入手，把创新教育渗透到课堂教学中，激发和培养学生的思维品质.

中学阶段，是思维最为活跃的阶段之一.在中学阶段，学生的求知欲最为强烈，并且理解能力和学习能力是最为活跃的，因此，对中学生进行发散思维能力的培养，从某种意义上来讲，是最有成效的.数学作为一门应用最为广泛、最能培养发散思维和问题解决能力的基础课程，其在培养学生的思维能力上具有独特的优势.因此，应当注重在中学数学教育中，将培养学生的创新能力、发散思维放在突出的位置上，以适应转型时代社会发展的需要.

发现式教学是基于布鲁纳的发现学习而提出的，是指在教师的指导下，通过阅读、观察、实验、思考、讨论等方式，引导学生发现问题，研究问题，进而解决问题、总结规律，成为知识的发现者.发散思维最基本的特色是：从多方面、多思路去思考问题.发现式教学培养学生发散思维有利于提高学生学习质量，有利于培养学生独立研究的能力，更有利于锻炼学生的思考能力.具体体现在以下几个方面：

一、营造环境，培养兴趣

在课堂上数学教师要善于用自己炽热的数学情感去调动、激发学生对数学学习的美好情感，营造一个良好的学习环境.在教学中，注意“课引”的设计，尽量使学生在一开始上课就对本节课怀有深厚的兴趣和好奇心.

案例1：在给初二学生第一次讲授不等关系时可以这样引入：阿凡提给巴依老爷放羊，羊越来越多，羊圈装不下了，可是小气的巴依老爷不愿多出做羊圈的栅栏，他让阿凡提自己想办法.阿凡提想出一个好办法：他首先把羊圈由长方形改建成正方形，这样就装下了.过了一年羊圈又装不下了，阿凡提又将正方形改建成圆形，又能把羊装下了.人们都夸阿凡提聪明.同学们想知道阿凡提这样做的根据吗？

这样就使本来枯燥的数学知识和我们的日常生活联系起来了，而且以故事形式表现出来，调动了学生的兴趣，活跃了课堂气氛，使学生的思维处于一种兴奋和开放的状态，这样容易培养其发散思维.

二、在课堂教学中应该适当给予学生思考的习惯与能力

在课堂上善于创设思维情景，引导学生积极思考，运用已学过的知识去解决新问题.其中组织课堂讨论是一种使用较普遍的有效方法.这样培养出来的学生敢于提问题、敢于批判、敢于质疑、思维敏捷，不受教师讲解的束缚，可为发散思维的培养创造良好的内、外部环境.

案例2：已知在平面直角坐标系中的三点A（1，0）、B（-1，0）、C（0，2），请你构造一些函数关系式或一些学过的图形，使其图像经过A、B、C三点，并写出函数关系式或图形的名称.

解析：我们的教学目的是希望学生阅读题目后，能尽可能多地写出满足题设的函数关系式或图形.如果学生最后能从下面的方面构造函数关系式或写出图形名称，那么我们的教学目的就达到了.

初中学生通过已学的知识可以从以下方向入手：

生1：从一次函数和分段函数着手构造.

生2：从二次函数着手构造抛物线函数关系式.

生3：构造等腰三角形.

生4：构造菱形.

生5：构造等腰梯形.

生5：构造圆形.

生6：构造圆锥体.

……

图1

通过这样的训练，注重学生思维能力的培养，训练创新思维.数学是思维的体操.因此，若能对数学教材巧安排，对问题妙引导，创设一个良好的思维情境，对学生的思维训练是非常有益的.在教学中应打破“老师讲，学生听”的常规教学，变“传授”为“探究”，充分暴露知识形成的过程，促使学生一开始就进入创新思维状态中，以探索者的身份去发现问题、总结规律.这样才能避免“死读书，读死书”的情况，使学生对所学的知识达到融会贯通，产生学习数学的喜悦情感，而不是让学生处于痛苦不堪的题海战术之中.

案例3：已知p+q+1＜0，求证：1位于方程x2+px+q=0的两根之间.

分析：对于此题，若按常规思路，先用求根公式求出方程的两根x1、x2，再求证结论，则将陷入困境，因此另觅新路.

证明：设y=x2+px+q，显然抛物线的开口向上.令x=1，则y=p+q+1.由已知p+q+1＜0，则点（1，p+q+1）在x轴下方（如图1）.

故原方程有两根x1、x2，且1位于这两根之间.

点评：这种解法通常称为“图像法”，当用常规方法不能解决问题时，应教授学生及时改变思路，另选突破口，切忌在原方法上徘徊.否则难以使思维发生质的飞跃，也不利于创造性思维的培养.

所以在学习数学的过程中，我们要着重训练学生“一题多解”“一题多变”“一法多用”的能力，从而最终实现促使其发散思维的培养和训练.

（一）一题多解.

指多角度考虑同一个问题，找出各方法之间的关系和优劣.“一题多解”之所以有助于发散思维的培养，主要是因为它要求学生的思维活动要“多向”，不局限于单一角度，不受一种思路的束缚，为了寻求问题的解决，它要求寻找多样化的解决方式，谋求多种可能.在这种情况下，学生往往会独辟蹊径，发现解决问题的新途径.

案例4：如图2，已知AB是⊙O的切线，切点为B，OA交⊙O于D，连接BD，BC⊥AO于点C，求证：∠1=∠2.

分析：利用条件（AB是⊙O的切线）的方法有多种，若要利用“弦切角定理”证明此题，就必须作出所对的圆周角，作法有如下三种.

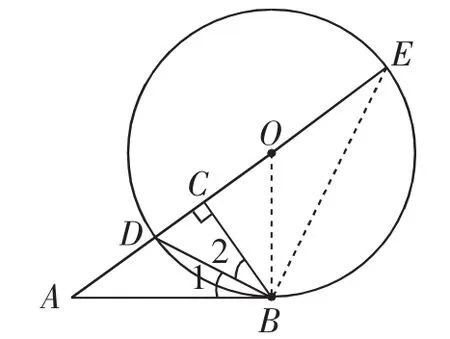
图3

证法1：如图3，延长AO交⊙O于点E，连接BE、OB，则∠2=∠E，∠DBE=90°.

由∠OBD=∠BDO，∠1+∠OBD=90°，得∠1+∠BDE= 90°.又∠E+∠BDE=90°，所以∠1=∠E.

故∠1=∠2.

证法2：如图4，延长BC交⊙O于点E，连接ED.

由弦切角定理，可得∠1=∠E.

由垂径定理，可知∠2=∠E.

故∠1=∠2.

图4

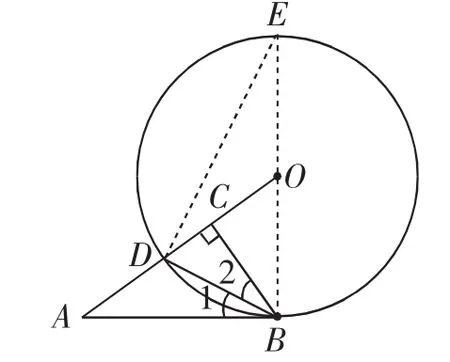
图5

证法3：如图5，连接BO并延长BO，交⊙O于点E，连接DE.

由弦切角定理，可得∠1=∠E=∠ODE.

由∠ODE+∠CDB=90°，∠2+∠CDB=90°，得∠ODE=∠2.

故∠1=∠2.

此题的三种证法，既有效地复习了“切线有关的性质”——切线的性质定理、弦切角定理、切线定理，又提高了学生应用切线性质的能力，培养了学生思维的广阔性和灵活性.同时，通过多种解法的比较，提炼出最佳解法，从而达到优化学生解题思路的目的.

（二）一题多变.

通过题目的引申、变化、发散，提供问题的背景，提示问题间的逻辑关系.“一题多变”之所以有助于发散思维的培养，主要是因为它要求学生必须形成知识系统，对不同知识之间的联系能通过自己以前所学的知识构筑起联系它们的桥梁.“一题多变”不仅培养了学生的发散思维能力，也极大地激发了学生学习数学的积极性和浓厚的兴趣.

“一题多变”的常用方法有：

1.变换命题的条件与结论；

2.保留条件，深化结论；

3.探讨命题的推广；

4.生根伸枝，图形变换.

我们仍然以案例4中的题为例，再通过如下变形，更进一步提高整体学习关于圆的相关知识和定理.

案例5：该题可以作如下变化：

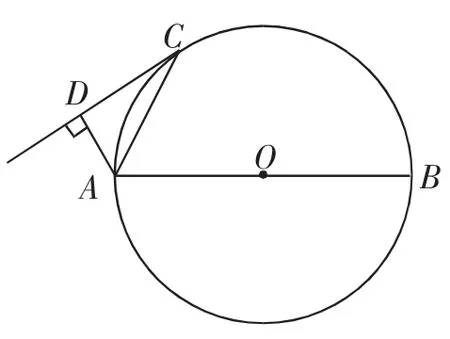
图6

变式1：如图6，已知AB是⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D，求证：AC平分∠DAB.

变式2：如图7，已知BC与⊙O相切于点B，CE垂直直径AF于点E，交弦AB于D，求证：CD=CB.

图7

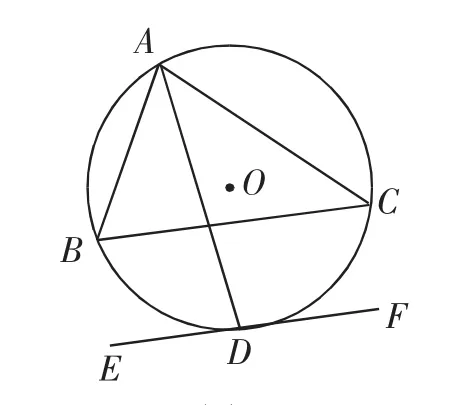
图8

变式3：如图8，△ABC内接于⊙O，AD平分∠BAC，交⊙O于D，过D作⊙O的切线EF，求证：EF∥BC.

通过对同一个题目的不同变形，我们又得到不同的证明结果，同时每一个结果的证明方法又可以是多样的，这样避免了学生陷入题海之中，同时也让学生发现了圆的各种相关知识和定理“万变不离其宗”的特点，大大提高了学生学习的兴趣.

（三）一法多用.

以一种方法处理相似或类似，甚至仅仅有部分条件相似的问题.“一法多用”可以使学生对所学过的知识的理解更加深刻，同样能够达到事半功倍的效果.

例如，我们在学习二元一次方程时，采取的求解方式就是联立方程.这个方法可以广泛地运用于求函数交点之中.

案例6：已知两个一次函数的表达式分别是y=3x-4和y=-2x+3，求两个函数的交点坐标.

分析：众所周知，一次函数实际上和二元一次方程息息相关，求两个一次函数的交点，其实就是求两个二元一次方程的公共解，所以我们只需要把两个函数联立即可.

（1）求两个函数的表达式；

（2）求直线与双曲线的交点坐标和△AOC的面积.

分析：根据△AOB的面积求出k=-3.

根据二元一次方程组求解的方法，联立两个函数关系式求解即可.

案例8：已知在坐标平面内有二次函数y=x2-2x和一次函数y=2x+2，求这两个函数的交点坐标.

分析：求交点坐标，案例6和7已经很明确地告诉我们，只需要将函数方程联立起来，求方程组的解，由此可知：然后求解一元二次方程x2-4x-2=0，得到x1=2+ ■ 6，x2=2- ■6.

由上述三题我们发现“一法多用“实际上能够让学生在学习数学过程中找到问题的规律及解决问题的方法，从而摆脱死读书、读死书、题海战术的桎梏.

三、在教学过程中恰当采取延迟评价的教学方法

这样可以给学生创设一种畅所欲言、互相启发的氛围，使学生在有限的时间内提出尽可能多的创造性设想，因而有助于培养学生的发散思维能力.学生思维启动的过程中别人的特别是老师的过早评价，往往会成为思维展开的抑制因素.正因为如此，我们在课堂上应当表现出极大的耐心，给学生充分的时间，让他们驰骋联想、各抒己见.在这种情况下，学生会有一种“安全感”“自由感”，从而无拘束、无顾虑地针对问题展开积极的思维活动和语言活动，起到相互启发的作用.这对小学、中学的教育来说都是一样的.

四、适当地在课堂上组织集体讨论

教师是课程进行过程中的引路人和指南针.但是不能形成教师的话就是“圣旨”，有时候也应该在课堂上组织一些集体讨论来培养学生的发散性思维.

集体讨论可分为2人小组、4人小组或全班讨论.这样的讨论没有教师的介入，有利于学生畅所欲言、集思广益，从而引发创造性思维的产生.在集体讨论中，学生的思维处于积极状态，所以集体讨论对思维能力的培养是有益的，对学生真正理解数学知识也是有益的.从表面上看，集体讨论时似乎课堂秩序有点儿乱，但如果学生真正是在参与讨论，甚至大声争论，那就是学生生动、活泼、主动学习的体现！

“业精于勤”.只要我们在教学中运用以上各种解题方法培养学生，让学生去理解各知识点之间的联系，触类旁通，使学生的思维时常处于多向、发散、开放状态，让他们去发现问题，从而使他们的思维上升到一个新的领域，使我们的数学教育真真正正发生“质”的变化，使数学能更好地为社会主义现代化服务，从而面向世界，面向未来！

1.罗增儒.数学解题学引论［M］.陕西：陕西师范大学出版社，2004.

2.罗增儒.中学数学课例分析［M］.陕西：陕西师范大学出版社，2001.

3.林崇德.教育的智慧写给中小学教师［M］.北京：开明出版社，1999.

4.王宪生.黄岗兵法变式题阵［M］.西安：陕西师范大学出版社，2003.

5.刘家松等.素质教育新教案（八年级下）［M］.北京：西苑出版社，2004.

6.冯大学，发现式教学法应用于新课标教材教学的实践与反思，《数学教学通讯》2010年第4期.