深究尺规作图，“牵出”全等三角形——全等三角形（第1课时）教学与思考

☉江苏苏州市高新区第一中学 单净璇

深究尺规作图，“牵出”全等三角形
——全等三角形（第1课时）教学与思考

☉江苏苏州市高新区第一中学 单净璇

全等三角形起始课是很多教研活动中的热点课题，因为这个课时的教学内容只需要关联少量的三角形概念和内角和，相对独立，不受教学进度太大影响，成为各级教研活动经常选用的比赛课时.然而这个课时的教学内容在各级教材上多是较为简单的全等图形、全等三角形的概念，简单识别全等三角形后找找对应边、对应角等训练，对多数学生来说，这节课有些消耗时间，硬把学生留在原地空转，而不涉及后续的全等三角形的判定公理，是值得商榷的.我们注意到全国著名特级教师李庾南老师在全等三角形起始课的教学时，就引导学生全面接触了全等三角形的判定方法，值得学习.受此启发，我们最近在教学全等三角形起始课时，也尝试了由尺规作图出发，“引出”全等三角形概念和一个公理的教学尝试，取得较为理想的教学效果.本文呈现这节课的教学设计，并跟进阐释教学立意，供研讨.

一、全等三角形起始课教学设计

【教学目标】在尺规作图中学习全等三角形的基本概念、一个公理（“边边边”）；理解并灵活运用全等三角形的性质（对应角相等、对应边相等）.

【重点、难点】识别经过“变换“之后的全等三角形的对应边、对应角.

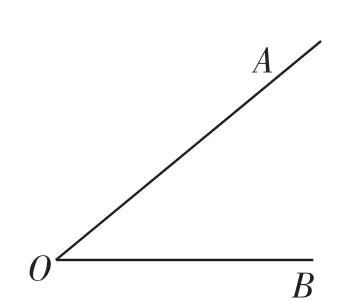
图1

【教学流程】

作图活动（一） 用尺规“复制”角.

如图1，作一个角等于∠AOB.

活动设计：教师示范尺规作图作出一个角等于已知角（如图2），并利用透明纸（或裁剪下来）比对两个角是否相等，说清背后的原理，给出公理，两个能完全重合的三角形称之为全等三角形，揭示全等三角形的判定公理SSS，并可适时链接到作平行线的方法.同时定义全等三角形、符号表示、相关概念等.

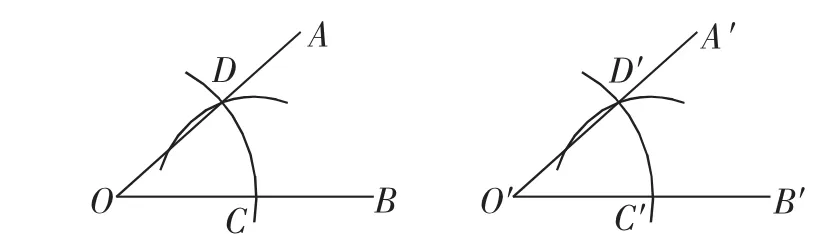
图2

作图活动（二） 用尺规“翻折”三角形.

如图3，将三角形ABC翻折，右侧为示意图形.

图3

活动设计：教师示范如何将一个三角形翻折，学生模仿操作，并追问，说说这两个三角形全等的依据，写出全等三角形符号表示，指出对应边、对应角.

作图活动（三） 用尺规“旋转”三角形.

如图4，尺规作图，将三角形ABC绕点B旋转得到三角形A′BC′（右侧为示意图）.

图4

活动设计：教师先示范旋转线段BA，将BA绕点B顺时针旋转一定角度到A′B的位置，分别以B、A′为圆心，BC、AC的长为半径作弧交于C′，则△A′BC′就可看成是△ABC旋转而来.追问：能否证明此时两个三角形是全等形？它们的对应角、对应边是哪些？并跟进设计一问：“求证：∠A′BA=∠C′BC.”

作图活动（四） 用尺规作出平行四边形.

如图5，以三角形ABC的三个顶点为顶点，再找一个点D，使点A、B、C、D围成平行四边形（两组对边分别平行的四边形为平行四边形）.

图5

活动设计：教师示范用圆规、直尺将一个三角形补成一个平行四边形，有三种可能的作法，先后呈现两种，追问学生是否还有不同的作法，引出经典问题：已知3个点探究第4个的位置，使这4个点能形成平行四边形.重点还在辨析这类四边形的由对角线分割之后的全等三角形及对应关系.可以针对其中一个平行四边形，提出证明题的要求，比如求证AB∥CD，或者提出问题“分析此时AB、CD之间的位置关系，并说明理由”.

课堂小结与解题训练：

1.如图6，对照下列图形，写出两个三角形全等的符号表达式，并指出对应边与对应角.

图6

2.如图7，下面是利用尺规作∠AOB的角平分线OC的作法：

①以O为圆心，适当长为半径画弧，分别交OA、OB于点D、E；

图7

③画射线OC，射线OC就是∠AOB的角平分线.

在上述用尺规作角平分线的过程中，请利用全等三角形的知识，解释OC为什么是∠AOB的角平分线.

设计意图：第1题是在不同的全等三角形图形中，引导学生识别全等三角形，找准对应关系，为后续全面、系统学习全等三角形的判定作好准备；第2题是训练角平分线的尺规作图与作图依据.

附：板书设计

二、教学思考

1.深刻理解全等三角形在几何中的地位，从“教教材”走向“用教材教”.

由于全等三角形在平面几何中的特殊地位，后续很多几何问题都需要建立在全等三角形的基础上进行研究，它是沟通边、角关系的重要工具，特殊三角形的性质、勾股定理的证明、平行四边形的判定与性质的探究、圆的学习等，都需要全等三角形的支持.而全等三角形的判定公理有多条，属于作图验证的公理.基于上述认识，我们决定“学材再建构”（李庾南老师新近提出的“三学”之一），即打破教材顺序，从尺规作图说起，先通过作图验证两个三角形重合的关键，定义全等三角形，给出“边边边”公理，真正践行从“教教材”走向“用教材教”（钟启泉语）.

2.基于尺规作图与全等三角形的关系，选定尺规作图驱动教学进程.

尺规作图博大精深，现行初中几何教学对尺规作图的要求整体不高，各级考试（特别是中考）往往也是考查简单的几种尺规作图，不少地区对这个考点甚至多年不考，这就影响了平时的几何教学，误以为这个知识点是可以淡化甚至忽略的.从上面的教学设计来看，各个环节都是在尺规作图的驱动下向前推进，每种尺规作图之后需要追问学生作图依据，组织推理语句、展示交流他们的理解.因为对于尺规作图的一些作法来说，更重要的是作图之后的推理证明，几何的理性思维也在于此.

3.注意平衡尺规作图与全等三角形新知之间的教学用时.

由于这是全等三角形起始课，而且各个教学环节都是由尺规作图驱动着前进，会给学生或听课老师一种错觉，误以为这是在专题学习尺规作图，故教师需要十分注意控制尺规作图作法上的时间，在归纳全等三角形新知、训练全等三角形符号表达、推理语句组织的教学活动上下足功夫，而不是整节课都是训练学生作图、纠正作法等偏离教学重点的教学行为.

三、写在后面

全等三角形在后续几何学习中价值巨大，奠基作用明显，缺它不可，同时全等三角形也与诸多数学知识联系紧密（如本课的“驱动问题”——尺规作图）.故对全等三角形起始课的教学研究也是热点课题，本文也是本着“同课异构”、殊途同归的教学追求，开展一次教学实践，有一定的教学可行性，但也不一定适合所有教师和学生，欢迎大家批评指正.

1.仇锦华.从数学整体观看单元教学［J］.中学数学教学参考（中），2015（11）.

2.刘东升.我们需要怎样的“问题”驱动课堂——由美国莎维女士执教的函数图像课说起［J］.教育研究与评论（课堂观察版），2016（11）.

3.顾为秀.从“标准”到“变式”，从封闭走向开放——以“全等三角形”起始课教学为例［J］.中学数学（下），2016（12）.

4.周红娟.从操作走向思考，从“参观”走向“探索”——“等腰三角形的性质（第1课时）”教学与反思［J］.中学数学（下），2014（7）.

5.郑毓信.“开放的数学教学”新探［J］.中学数学月刊，2007（7）.