归类新定义考题，明辨“同与不同”——以两道新定义考题为例

☉江苏昆山市娄江实验学校 胡 俊

归类新定义考题，明辨“同与不同”
——以两道新定义考题为例

☉江苏昆山市娄江实验学校 胡 俊

新定义考题是近年来不少地区中考一道亮丽的风景线，个别省市各区的模考卷几乎“一时新风”，其中出现不少优秀的新定义考题.本文拟结合两道解法趋同的新定义考题，讲解思路，并跟进教学思考，供分享.

一、两道新定义考题的思路突破

考题1：在平面直角坐标系xOy中，A（t，0）、B（t+对于线段AB和x轴上方的点P给出如下定义：当∠APB=60°时，称点P为AB的“等角点”.

（2）直线MN分别交x轴、y轴于点M、N，点M的坐标是（6，0），∠OMN=30°.

①线段AB的“等角点”P在直线MN上，且∠ABP= 90°，求点P的坐标；

②在①的条件下，过点B作BQ⊥PA，交MN于点Q，求∠AQB的度数；

③若线段AB的所有“等角点”都在△MON内部，则t的取值范围是__________.

思路突破：首先理解新定义，根据A、B点的坐标特征，可确认线段AB的长为 ■ 3，由∠APB=60°想到等边三角形ABP，进而想到△ABP的外接圆，从而想清图1这样的圆弧，即优弧APB上任意一点都是符合要求的“等角点”.接着想清该外接圆的圆心、半径等信息，经过确认应该能得出圆K的半径AK为1，弦心距.还需要说明的是，定义中指出“线段AB和x轴上方的点P”，忽视这里的“x轴上方”则容易错误理解成x轴下方的情形（如图2）.

图1

图2

接着求解第（1）问，精准构造图3，就可确认点C、D在优弧AB上，而点E在圆K外部，不是等角点.教学时需要提醒学生精准作图，否则容易造成错解.另外，如果构造图形有误差，需要结合这些数据的特点进行校正.比如C、E两点都在直线上，A、E两点都在直线x=上，这样也有助于认识点E在圆K外的位置关系.

图3

（2）①分两种情况.

若N点在y轴的正半轴上，构造图4分析.由∠APB= 60°，∠ABP=90°，得∠PAB=30°.又∠OMN=30°，所以PA= PM，AB=BM.易得BM=AB= ■ 3，所以PB=1，即P（6-

图4

图5

类似的，若N在y轴的负半轴上，构造图5分析.

②先考虑N在y轴正半轴上的情形，构造图6分析.

由BQ⊥AP，且∠APB=60°，∠PBQ=30°，可得∠ABQ=60°，所以∠BMQ=∠MQB=30°.所以BQ=BM= AB.于是确认△ABQ是等边三角形.即∠AQB=60°.

类似的，当点N在y轴负半轴上时，类比分析.

③若线段AB的所有“等角点”都在△MON内部，就是优弧在△MON内部，容易发现该圆左侧与y轴相切（如图7）、右侧与MN相切（如图8）是两次临界状态.

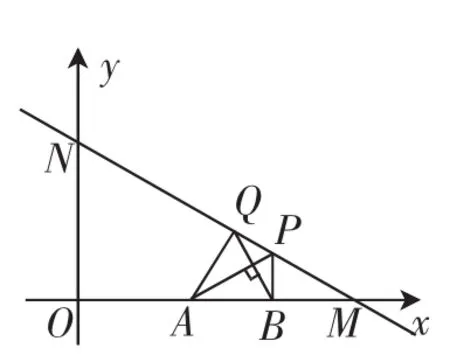
图6

图7

图8

接下来分析出图7、图8中点A的坐标即可.让我们把图7再次“放大”，以便更好地“暴露“图形中的细节与解法步骤，如图9，O′H=，OH=O′A=O′D=1，此时OA=OH-

图9

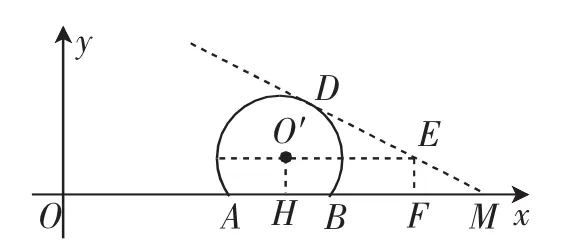
图10

考题2：如图11，对于平面直角坐标系xOy中的点P和线段AB，给出如下定义：如果线段AB上存在两个点M、N，使得∠MPN=30°，那么称点P为线段AB的伴随点.

图11

（1）已知点A（-1，0）、B（1，0）及D（1，-1）、

①在点D、E、F中，线段AB的伴随点是_________；

②作直线AF，若直线AF上的点P（m，n）是线段AB的伴随点，求m的取值范围.

（2）平面内有一个腰长为1的等腰直角三角形，若该三角形边上的任意一点都是某条线段a的伴随点，请直接写出这条线段a的长度的范围.

思路简述：首先想清新定义的图形结构，构造图12进行分析，与考题2相比，这里的优弧AB有两段分布在x轴上、下方，且这两段优弧围成区域内部（除AB线段上的点）所有点都是符合要求的所谓“伴随点”.

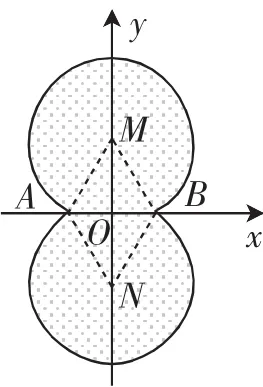
图12

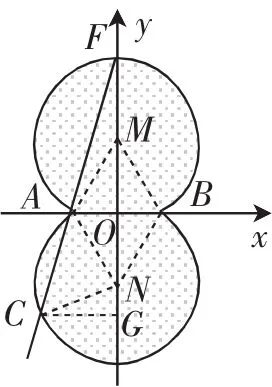
图13

图14

（1）①把三个点在图12中标出来就可确定只有点D、F符合要求.

（2）如图14，将该等腰直角三角放置于阴影区域内时，恰能被完整覆盖，此时直径为，半径为，也就是AB为，即

二、教学思考

1.审题要慢，理解新定义的图形结构是解题关键.

新定义考题需要理解图形结构，并对关键词句隐含的限制信息充分解读，对应到构造中去.这类习题往往与一些特殊图形有关，如特殊直角三角形、外接圆等知识，需要解读、构图.同时有些隐含信息的解读也很关键，如考题1中如果忽略“x轴上方的点P”可能造成复杂的构造与多解，而考题2又需要想清两段优弧及其内部的区域都是伴随点.

2.归类新定义考题，引导学生感受“同与不同”.

经过教学实践，将考题1、考题2归类讲解可以使学生感受到这类问题的类似结构，这里的“同与不同”对比明显，如考题1只是一段优弧，而考题2则是两段优弧及其内部区域（线段AB除外）.通过“形异质同”考题的呈现，可以促进学生“做一题，会一类”.同时也能学会这类考题的解题策略、读题策略，特别是不漏掉一句甚至一个字符.

3.开展解后反思，明辨解题所需的重要知识点.

倡导解后反思是解题教学的重要环节，如考题1解答之后，不但要让学生明白阅读理解新定义，想清“优弧”结构的重要性，同时要引导学生积累解题策略，如善于在分析问题过程中适时分离图形、放大局部图形（如图9、图10）；而考题2求解过程中，在图13、14中构造特殊直角三角形，实现问题思路贯通，这些都需要在反思回顾时想清，并做好相关解题经验的积累.

三、写在最后

新定义考题是近年来北京地区比较重要的一类考题，对各地的考题走向都带来了不小的影响.然而应对新定义考题的备课研究，特别是围绕优秀考题的“一题一课”的课例研究还有待丰富，本文也只是尝试将两道类似考题集中在一起进行解法的探究，还有待重组、设计成课例，以便从解题探究走向解题教学的研究.

1.沈丽婧.聚焦微专题：中考二轮复习的实践与思考——以一组“关联试题”复习为例［J］.中学数学（下），2017（3）.

2.甘晓云.以退为进：挑战新定义考题的有效策略——北京海淀九上期末卷第29题解析与赏析［J］.中学数学（下），2017（2）.