斜简支梁桥支点剪力计算方法的研究

宋娃丽，史帆，王荣霞

（河北工业大学土木与交通学院，天津300401）

斜简支梁桥支点剪力计算方法的研究

宋娃丽，史帆，王荣霞

（河北工业大学土木与交通学院，天津300401）

以某斜简支T形梁桥为研究对象，通过建立空间力学模型，分析了不同斜度下斜梁桥的荷载传递机理，并计算和比较了由汽车荷载所引起的正交桥与斜桥的支点剪力，指出杠杆原理法在斜梁桥内力计算中的局限性.为优化斜梁桥在汽车荷载下支点剪力的计算方法，提出混合影响线法并明确了斜梁桥通过混合影响线法计算支点剪力的具体步骤.通过该方法计算得到的斜梁桥内力结果与模型计算结果相符，且该方法理论明确，计算简便，可应用于工程实际.

斜简支梁桥；支点剪力；混合影响线；汽车荷载

0 引言

当道路在选线的过程中受到障碍物或建筑物的限制时，为了更好地适应地形地物，往往需要考虑修建斜桥[1].在我国，关于正交桥的理论知识体系已经建立得比较完善[2]，而关于斜桥的受力特性及设计计算等方面的内容尚需深入研究[3].外国学者在20世纪50年代就对斜桥展开研究并取得了一些成果：Chen[4]运用变分法研究了不同刚度下的斜肋梁板的弯矩和挠度变化并提出了与之相对应的影响系数；Bakht[5]针对斜梁桥利用对半连续梁法对其进行简化并进行了详细的计算与分析；Harry W.Shenton[6]研究了斜钢板桥的荷载横向分布.我国学者席振坤[7]在20世纪80年代依据《公路桥涵设计通用规范（JTJ 021-1989）》[8]的荷载标准及公路等级提出了用有限元分析横向绞结的斜梁（板）桥的方法，并给出了不同斜度、板梁数、弯扭参数的绞结板桥纵向内力的折减系数.余泉[9]对简支斜小箱梁桥的受力行为和荷载横向分布进行了分析研究并提出了计算其荷载横向分布的修正刚接梁法；谭俊[10]考虑了斜梁桥弯扭耦合效应，建立了利用传递矩阵法求解多梁式斜梁桥荷载横向分布系数的弹性横梁法，并与刚性横梁法及有限单元法的计算结果进行比较；龙形航[11]对斜梁桥结构理论和计算方法进行深入分析，总结了斜梁桥在进行荷载横向分布计算时用到的几种适用方法.总之，上述工作均从不同方面揭示和研究了斜桥的部分受力特点和设计计算方法，但随着《公路桥涵设计通用规范（JTG D60-2004）》[12]及《公路桥涵设计通用规范（JTG D60-2015）》[1]的提出，公路桥梁荷载等级及计算标准又发生了新的变化，原有的部分方法已经不适宜解决在新规范下斜桥的内力计算问题，此外，由于斜桥弯扭耦合效应明显，其受力特性与横向刚度关系密切，且目前还没有在新规范下考虑斜梁桥横向刚度的支点剪力理论计算方法.因此，本文依据《公路桥涵设计通用规范（JTG D60-2015）》为解决斜梁桥在活载（公路-Ⅰ级荷载）下支点剪力的理论计算，提出了混合影响线法，并通过建立不同斜度的斜梁桥Midas模型，比较了混合影响线法和有限元方法计算支点剪力的结果，验证了本方法的正确性和适用性.

1 斜梁桥的荷载传递机理

斜桥一般包括斜梁桥、斜拱桥、斜刚架桥等桥梁形式[2-3]，其中斜梁桥为区别于正交梁桥的桥轴线法线与支承边有一定夹角的梁桥，如图1所示.图中α为斜度，即指桥轴线法线与支承边之间小于90°的夹角，以表示斜梁桥的倾斜程度.

某跨径为13 m的简支斜梁桥，宽16.75 m，由11片梁组成，主梁采用等高度预应力混凝土T形梁，并以湿接缝连接，桥梁横断面见图2，主梁细部尺寸见图3.

图1 斜梁桥示意图Fig.1 Diagram of the skew beam bridge

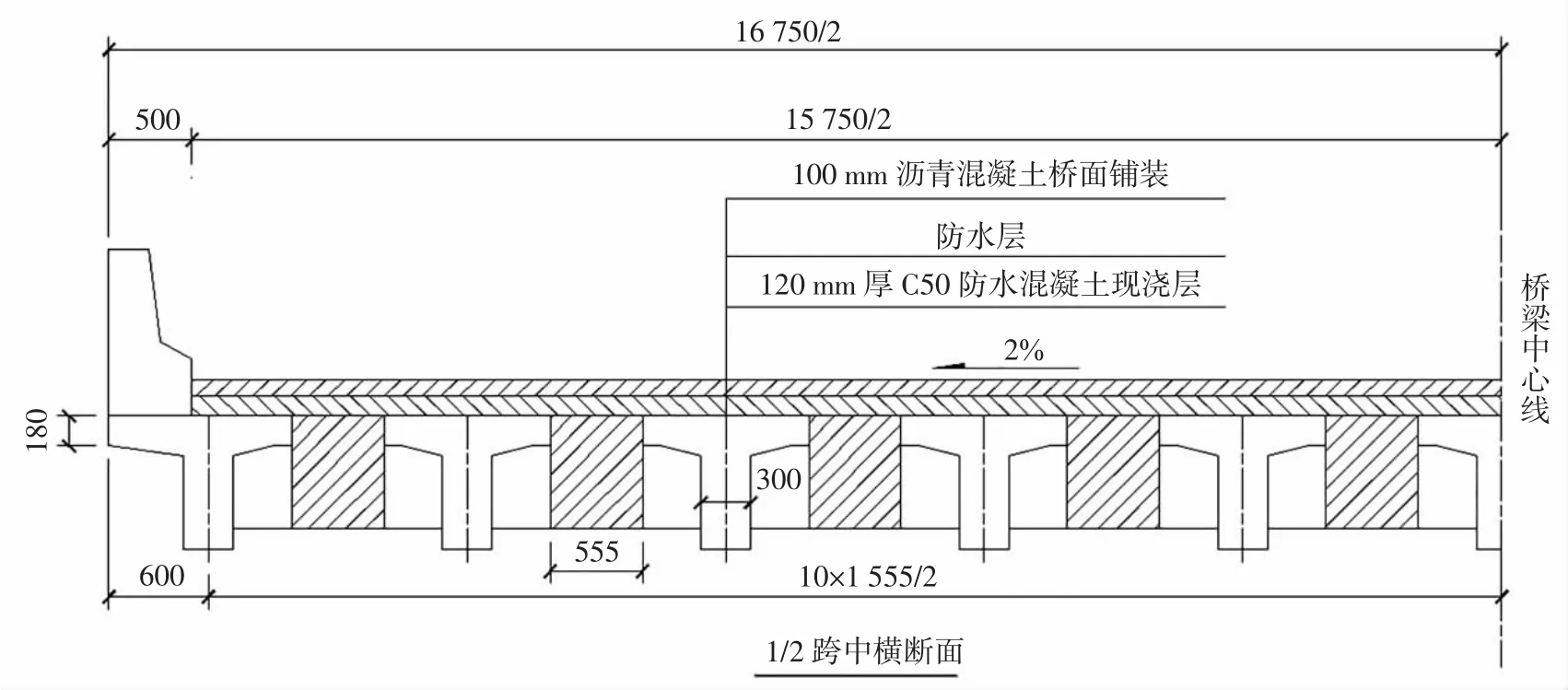
图2 桥梁横断面图（单位：mm）Fig.2 Cross section of the bridge（mm）

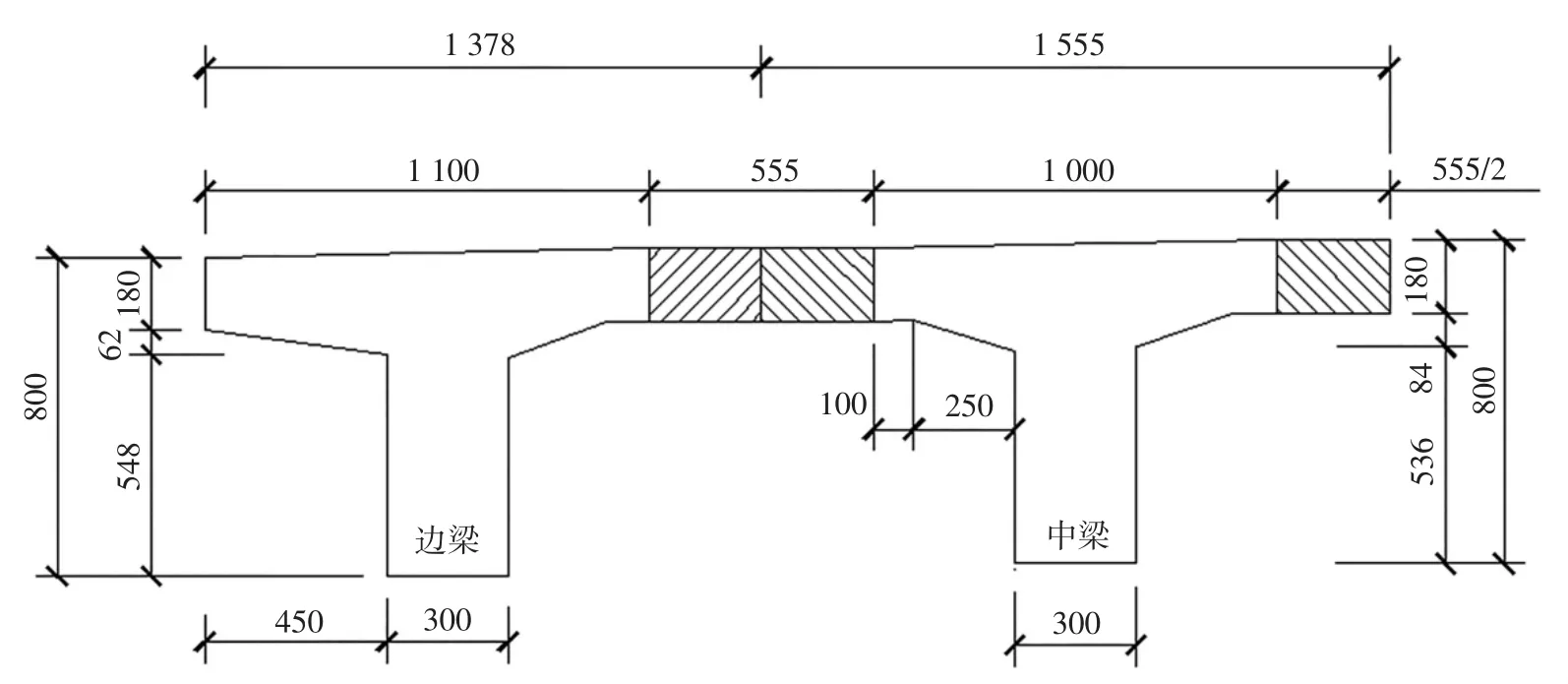
图3 主梁细部尺寸（单位：mm）Fig.3 Size of main beam in detail（mm）

对此桥梁的计算采用空间杆系有限元法，运用Midas/civil软件分别建立斜度为0°、15°、30°、45°的梁格模型，并计算在2号梁跨中截面集中荷载作用下的全桥位移等值线及全桥最大弯矩传递方向线，计算结果如图4～图7所示.

图4 正交（0°）2号梁跨中集中荷载作用下的荷载传递Fig.4 Load transfer mechanism of the second beam（0°）

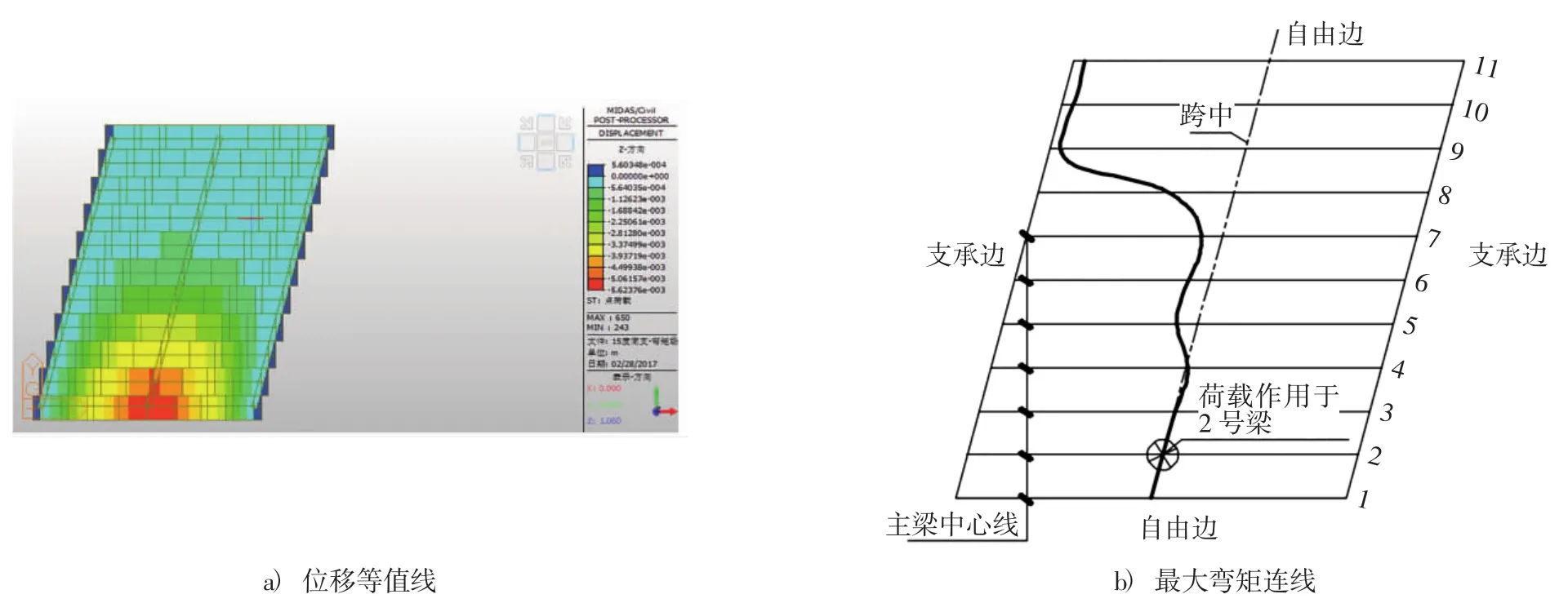
图5 斜交（15°）2号梁跨中集中荷载作用下的荷载传递Fig.5 Load transfer mechanism of the second beam（15°）

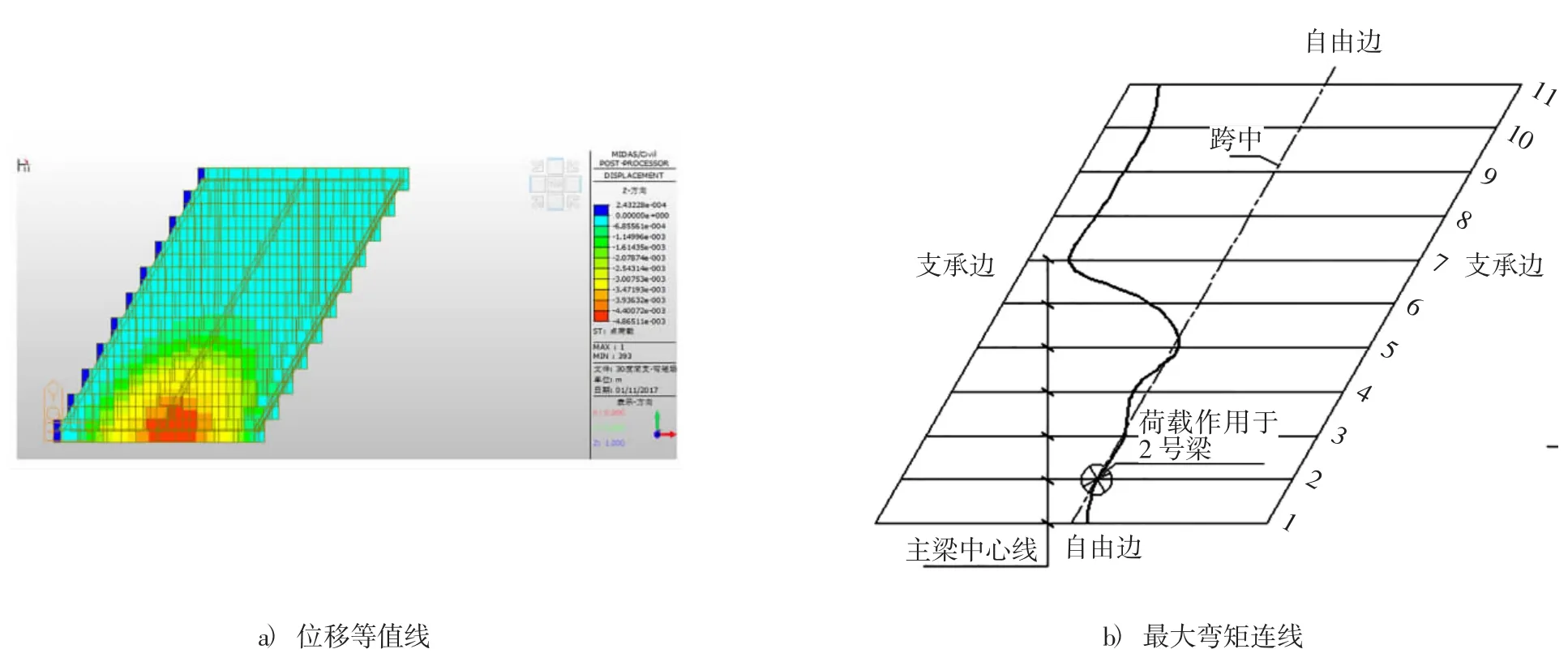
图6 斜交（30°）2号梁跨中集中荷载作用下的荷载传递Fig.6 Load transfer mechanism of the second beam（30°）

图7 斜交（45°）2号梁跨中集中荷载作用下的荷载传递Fig.7 Load transfer mechanism of the second beam（45°）

从图4～图7可以看出，与正交桥梁不同的是，斜简支梁桥最大弯矩的连线是先沿各梁跨中连线传递然后开始向自由边方向（桥梁钝角处）发展的，且随着斜度的增大，向自由边方向发展的趋势出现的越早，跨中最大弯矩的横向传递线与各梁跨中连线的分离程度随斜度的增大而增大.这些特征对斜交桥梁的支点受力产生了一定影响.

2 Midas模型的验证

为验证Midas模型建立的合理性，本文针对正交桥的支点剪力进行了进一步的理论计算.在实际的桥梁支点剪力的理论计算中，为将空间问题转化为平面问题，常引入横向分布系数的概念[1-2].对于正交桥，计算支点截面的横向分布系数一般采用杠杆原理法，其基本假定是忽略主梁之间横向结构的联系作用，即假设桥面板在主梁上断开，而当作沿横向支承在主梁上的简支梁或悬臂梁来考虑[2，13].

如图8所示，以3号梁为例，若采用杠杆法计算作用于3号梁的车轮影响线纵标，在影响线区域（2～4号梁之间）外的车轮对其是没有影响的.计算结果如表1所示.

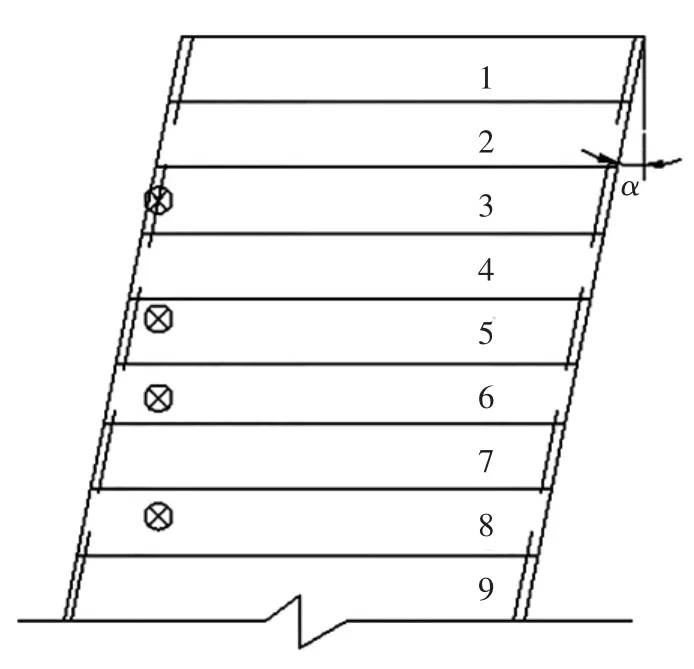
图8 斜梁桥的车辆布置Fig.8 Vehicle arrangement of skew bridge

表1 正交桥Midas软件与杠杆原理法计算公路-Ⅰ级荷载下的支点剪力kNTab.1 Shearing force of orthogonal bridge with theoretical model and mixed influence line method

由表1可知，通过杠杆原理法与Midas软件得到的正交桥在公路-Ⅰ级荷载下的支点剪力值相对误差为5.82%～8.05%，说明Midas软件空间模型建立合理.

3 Midas软件计算斜桥支点剪力

运用Midas软件计算不同斜度的斜桥在公路-Ⅰ级荷载作用下的支点剪力及其与正交桥支点剪力的比值，结果见表2.

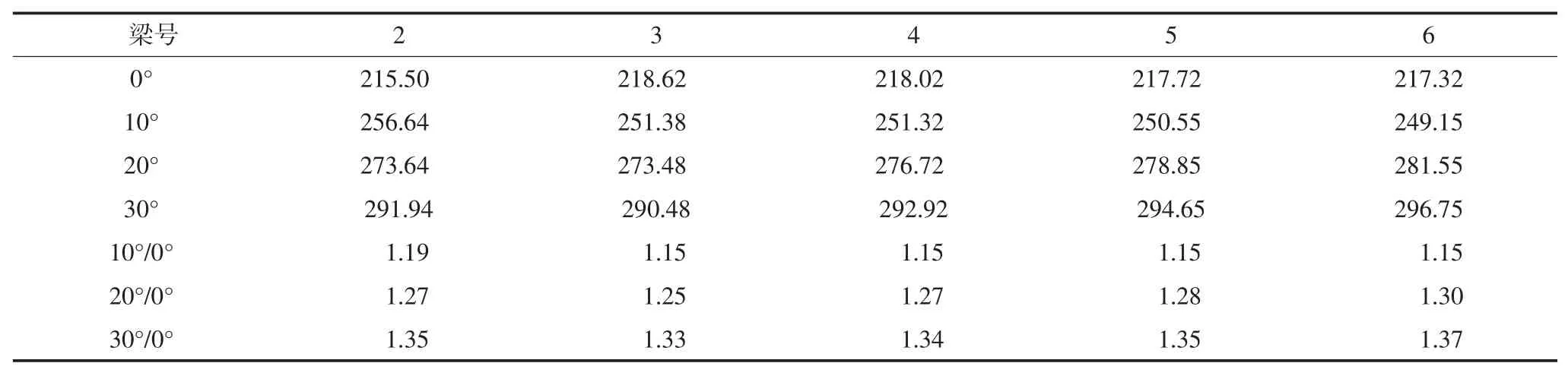
表2 Midas软件计算不同斜度斜桥公路-Ⅰ级荷载下的支点剪力kNTab.2 Shearing force of skew bridge in different angles with theoretical model

表2的计算结果表明，随着斜度的增大，斜交桥支点剪力与正交桥之比由平均1.15倍增大到平均1.35倍，且各号梁的支点剪力增长倍数仅相差4%～5%.上述结果表明，在实际设计时，若采用与正交桥相同的杠杆原理法计算斜桥的支点剪力，其结果往往比实际值偏低，理论计算与实际受力效应数值差达15%～35%，严重影响了构件安全，需对原计算方法进行适当改进.

4 混合影响线法计算斜桥结构内力

对于正交桥来说，其在活载下的支点剪力可以采用杠杆原理法进行计算[2]，而对于斜桥来说，如图8所示，以3号梁为例，作用于5号梁、6号梁和8号梁的车轮对3号梁的车轮影响线会有弹性分布影响[14].对于作用在支点处的荷载可以采用杠杆原理法进行计算，而对于非作用在支点处的荷载应充分考虑桥梁横向刚度使其合理分配于周围的梁[15-16].因此，本文通过混合影响线法解决非作用在支点处荷载所引起的支点剪力计算方法.

考虑到本斜梁桥横向刚度较大，对于不在支点处的荷载可以采用刚接板梁法对其进行分配并得到相应的影响线坐标.同时，根据前述斜梁桥的荷载传递机理，可以假定荷载横向分布取垂直于自由边的方向，又根据荷载在主梁上的作用位置，则可以对应取正交桥跨中截面或考虑横向分布系数沿桥跨的变化段内插从而得到横向分布影响线坐标，此种计算横向分布影响线的方法即为混合影响线法.即当计算斜梁桥的支点剪力时，首先应同时绘制杠杆原理法和刚接板梁法的荷载横向分布影响线并得到交点，其次考虑横向分布系数沿桥跨的变化绘制混合影响线，最终通过混合影响线法得到斜梁桥的支点剪力值.采用混合影响线法计算得到的简支斜梁桥支点剪力结果同时考虑了桥梁斜度和横向刚度两个影响因素，与斜梁桥实际结构受力状态更加吻合.

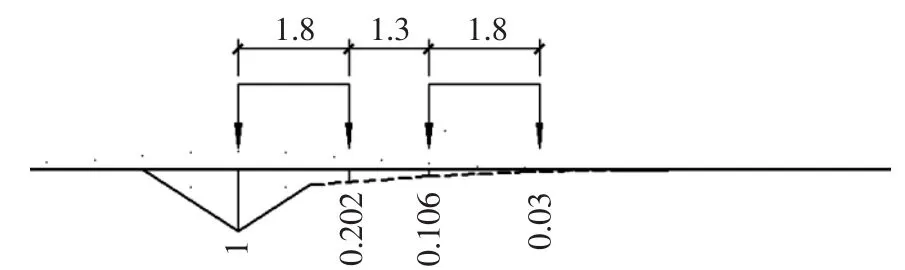
图9 3号梁混合影响线Fig.9 Mixed influence line of the third beam

以图2所示的结构为例，若采用混合影响线法对荷载横向分布系数进行计算，则其混合影响线中的实线为杠杆法结果，虚线为刚接板梁法结果，如图9所示.同时又可知，3、4列车汽车横向折减系数分别为0.78和0.67[1]，则由此两列汽车进行偏载控制设计，得到3号梁的支点截面横向分布系数为0.669，而相同荷载作用下的正交桥的结果为0.579.

此外，采用混合影响线法时由斜梁桥荷载传递机理，横向分布系数沿桥跨变化，当斜度α＜30°时，由支点横向分布系数至跨中截面横向分布系数的变化段长应取L/5（L为计算跨径）；当斜度30°＜α＜45°时，变化段长可取L/4.且当α=0°即为正交桥时，混合影响线法结果与杠杆原理法结果一致.

5 混合影响线法与Midas/civil软件模型结果的对比

以图2所示结构，分别用Midas软件及混合影响线法计算公路-Ⅰ级荷载下的30°斜交梁桥的2～6号梁（1号梁不控制设计）的支点剪力（未计冲击力），并比较其计算结果，见表3.

表3 斜度30°时Midas软件与混合影响线法公路-Ⅰ级荷载下的支点剪力kNTab.3 Shearing force of bridge in thirty degrees with theoretical model and mixed influence line method

由表3可知，斜交30°梁桥混合影响线法与Midas软件计算值相对误差为3.52%～6.15%，且混合影响线法计算的结果值偏大，则说明混合影响线法满足精度要求并偏于安全.

6 结论

通过本文的理论及计算分析，可得出如下结论：

1）斜梁桥荷载横向分布的路径都有垂直于自由边方向发展的趋势，且随着斜度的增大，此趋势出现的梁号越接近于荷载直接作用的梁号.

2）对于采用横向湿接缝连接的斜T形梁桥，汽车荷载引起的支点剪力随斜度的增大而增大，斜度为30°的斜桥的支点剪力约为正交桥的1.35倍.在实际设计时，若采用与正交桥相同的支点剪力法计算斜桥的支点剪力，主梁可能因混凝土斜截面的抗剪承载力不足而出现斜裂缝.

3）计算斜梁桥的支点剪力时，可采用混合影响线法，即同时采用杠杆原理法和刚接板梁法绘制其荷载横向分布影响线以得到两影响线的交点，并考虑横向分布系数对于不同的斜度α需采用不同的变化段长度，绘制混合影响线.

4）通过混合影响线法计算得到的简支斜梁桥支点剪力结果同时考虑了桥梁斜度和横向刚度两个影响因素，所得到的计算结果不仅满足在新规范下斜梁桥设计的要求且偏于安全，同时此方法理论明确，计算简便，可用于工程实际.

[1]JTG D60-2015，公路桥涵设计通用规范[S].北京：人民交通出版社，2015.

[2]项海帆.高等桥梁结构理论[M].北京：人民交通出版社，2013.

[3]黄平明.混凝土斜梁桥[M].北京：人民交通出版社，1999.

[4]Bakht B.Analysis of some skew bridges as right bridges[J].Journal of Structural Engineering，1988，114（10）：2307-2322.

[5]Bishara A G，Liu M C，El-Ali N D.Wheel load distribution on simply supported skew I-beam composite bridges[J].Journal of Structural Engineering，1993，119（2）：399-419..

[6]Huang Haoxiong，Shenton Harry W，Chajes Michael J.Load distribution for a highly skewed bridge：testing and analysis[J].Journal of Bridge Engineering，2004，9（6）：558-562.

[7]席振坤.横向铰接斜梁（板）桥实用计算法[M].北京：人民交通出版社，1991.

[8]JJTJ 021-1989，公路桥涵设计通用规范[S].北京：人民交通出版社，1989.

[9]余泉.多箱式连续小箱梁桥受力特性的分析及其试验研究[D].杭州：浙江大学，2006.

[10]谭俊.荷载横向分布的弹性横梁法[D].长沙：长沙理工大学，2014.

[11]龙形航.简支转连续斜T梁桥空间受力分析[D].长春：吉林大学，2015.

[12]JTG D60-2004，公路桥涵设计通用规范[S].北京：人民交通出版社，2004.

[13]彭卫兵，赵麒麟，潘晓东，等.基于实体单元的桥梁截面内力计算研究[J].土木工程学报，2012，45（9）：91-99.

[14]He X H，Sheng X W，Scanlon A.Skewed concrete box girder bridge static and dynamic testing and analysis[J].Engineering Structures，2012，39（6）：38-49.

[15]马占海.斜交板梁桥的横向受力理论计算与试验分析[J].交通科技，2015（2）：40-41.

[16]王秀艳.基于JTG D60-2004规范的斜板桥实用计算方法研究[D].上海：同济大学，2008.

[责任编辑 杨屹]

Study on shearing force calculation method for skew simply beam bridge

SONG Wali,SHI Fan,WANG Rongxia
（School of Civil Engineering and Transportation,Hebei University of Technology,Tianjin 300401,China）

For a skew T-beam supported simply bridge,the space mechanics model established to calculate and compare the shearing force caused by vehicle load,and analyze the load transfer mechanism of skew beam bridge with different angles.The limitations of lever principle method is indicated.In order to optimize the traditional calculation method for shearing force,the mixed influence line method is proposed and the procedure of this method is cleared.The results obtained with mixed influence line method agree with the theoretical model value,and this method is practical.

skew simply beam bridge;shearing force;mixed influence line;vehicle load

U441.5

A

1007-2373（2017）02-0113-06

10.14081/j.cnki.hgdxb.2017.02.019

2017-02-27

2016年廊坊市科技支撑计划（2016013073）

宋娃丽（1964-），女，教授．