组合受力钢筋混凝土环形截面构件极限承载力研究

王蒙，王璞，黄真

（上海交通大学船舶海洋与建筑工程学院，上海200240）

组合受力钢筋混凝土环形截面构件极限承载力研究

王蒙，王璞，黄真

（上海交通大学船舶海洋与建筑工程学院，上海200240）

基于变角空间桁架理论对钢筋混凝土环形截面构件在拉压弯剪扭组合受力下的极限承载力计算模型进行了研究，具体研究内容包括构件破坏截面几何形式表达和极限承载力计算公式.首先依据变角空间桁架理论推导出在拉压弯剪扭组合受力下的钢筋混凝土环形截面构件的破坏面倾角表达式.据此确定破坏面几何形状，并对破坏面一侧隔离体建立极限平衡方程，获得组合受力的钢筋混凝土环形截面构件承载力计算模型表达式.并将推导的钢筋混凝土环形截面构件承载力计算模型表达式与相应的试验研究结果进行比较.

钢筋混凝土；环形截面；组合受力；极限承载力

0 引言

钢筋混凝土环形截面构件常应用于桥梁结构及一些特殊结构，如石油管道结构等.在自重、水土压力、风荷载等作用下，钢筋混凝土结构破坏大多由构件或节点在拉压、弯、剪、扭4种组合作用[1]下引起的。目前既有研究和规范[2-4]对单一受力作用下的钢筋混凝土构件极限承载力已有了较好的计算方法，但是对于拉压弯剪扭组合受力的钢筋混凝土构件承载力计算常常基于经验公式，对环形截面构件则缺乏统一的理论基础和计算模型.

有关于钢筋混凝土组合受力构件极限承载力的研究，绝大部分是基于矩形和箱型截面构件展开的，基于环形截面构件的研究则非常稀少.对于环形截面构件领域，2012年，霍锦峰[5]骆华勋[6]刘西拉对统一破坏模型进行了推导.刘西拉等人的研究，通过将钢筋离散将钢筋混凝土等效为均质材料，对均质材料的承载能力进行推导；本文研究则是基于变角空间桁架模型，建立包含钢筋和混凝土的隔离体模型，通过极限状态下的隔离体的受力分析建立承载力表达式.

针对拉压弯剪扭复合受力构件的承载力计算，变角空间桁架理论[7]是目前应用较为广泛的方法，已有相关文献针对矩形和箱型截面构件进行了研究[8-10].本文应用变角空间桁架模型，分析推导钢筋混凝土环形截面构件在拉压轴力、弯矩、剪力、扭矩共同作用下的破坏模式和极限承载力表达公式，并与一些现有试验结果比较.由于本文是基于静荷载工况建立理论模型，推导的极限承载力表达式也仅适用于静荷载工况，对于动荷载工况尚需进一步研究.

1 理论模型

1.1 计算假定

本文根据变角空间桁架理论模型，推导出环形截面构件破坏时，轴压力、扭矩、剪力、弯矩间的强度相关方程.对于理论模型，作如下2个假定：

1）构件达到极限扭矩时，假定全部箍筋受拉屈服、裂缝处纵筋受拉屈服、受压区纵筋受压屈服. 2）近似认为剪力流中心线、箍筋的内皮、纵筋到环形截面中心距离相同，记为

1.2 确定破坏面形式

裂缝先在截面下端混凝土受拉区产生，在两侧以不同的裂缝倾角向受压区发展，最后在受压区闭合.如图1所示，黑色部分为混凝土受压区.本文以图示顶部混凝土压碎宣告完全丧失承载力.

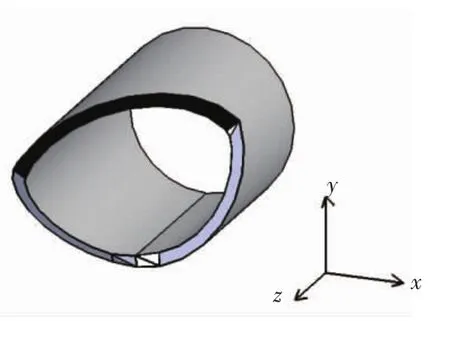
图1 环形截面构件破坏形式Fig.1 Failure mode of the annular section member

1.3 计算破坏面裂缝倾角

基于变角空间桁架理论模型，裂缝间的混凝土形成压杆，纵向钢筋和箍筋则形成拉杆，裂缝间混凝土不传递力.

计算时取侧壁壁厚近似处处相等，设由扭矩T产生的剪力流qt在环形截面均匀分布：

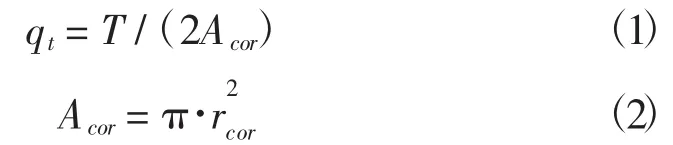
由剪力产生的剪力流在2个环形侧壁中发生，且为均匀分布得：

将扭矩产生的剪力流与剪力产生的剪力流叠加，由公式（1）～公式（3）分别得到两侧壁的剪力流：

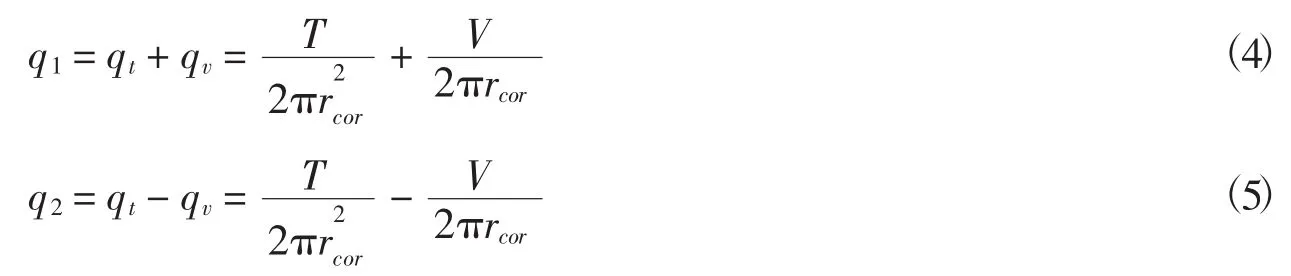
取隔离体如图2所示，隔离体为裂缝下方到环形截面最低点的部分.

图2为从环形截面截取一段侧壁的受力.对此隔离体，由于裂缝处混凝土不传力，其在图示y方向受力为2部分：1）混凝土环形侧壁剪力在y方向的分量，其值为剪力流q在y方向分量对侧壁弧长的积分；2）裂缝处箍筋拉力在y方向的分量，其值为各箍筋拉力y方向分量的和，此处将离散分布的箍筋等效为相同配筋率下的连续分布，则其中轴心张角dφ对应裂缝处的箍筋数量为rcordφcotθ/s由y方向上的静力平衡得到：

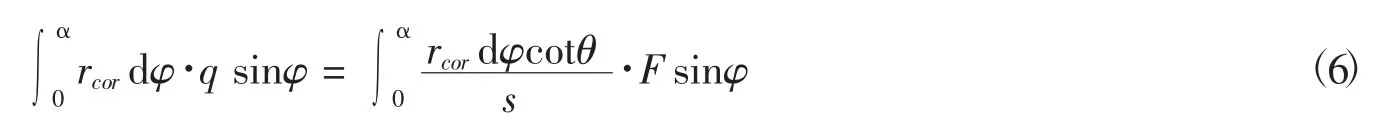
F为单肢箍筋的拉力，由于假定箍筋全部屈服，则有：

图2 裂缝下方侧隔离体Fig.2 Free body under the crack

由于假定了裂缝处箍筋全部屈服，本公式适用于剪力或扭矩较大的情况.

公式（6）整理得：

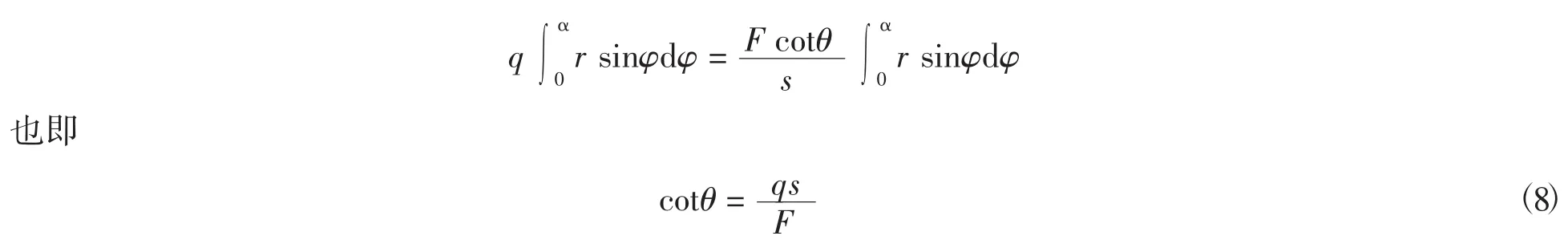
由于两侧壁的剪力流大小不同，两侧的倾角也不相同，将公式（4）和公式（5）代入公式（6），据此可以得知两侧壁裂缝的倾角

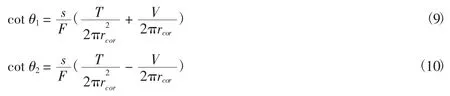
1.4 计算混凝土受压区高度

受压区钢筋全部受压屈服，受压区混凝土达到抗压强度，裂缝处纵筋全部受拉屈服，则由正截面z方向受力平衡得：

整理得：

式中：A为环形截面截面积.则等效受压区混凝土中心到环形截面中心的距离r′可由以下积分获得：

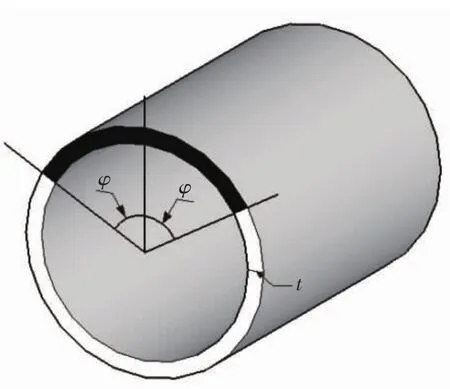
图3 混凝土受压区示意图Fig.3 Compression area of the concrete

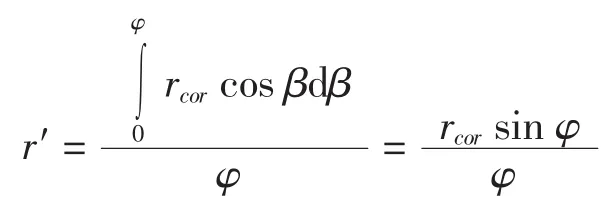
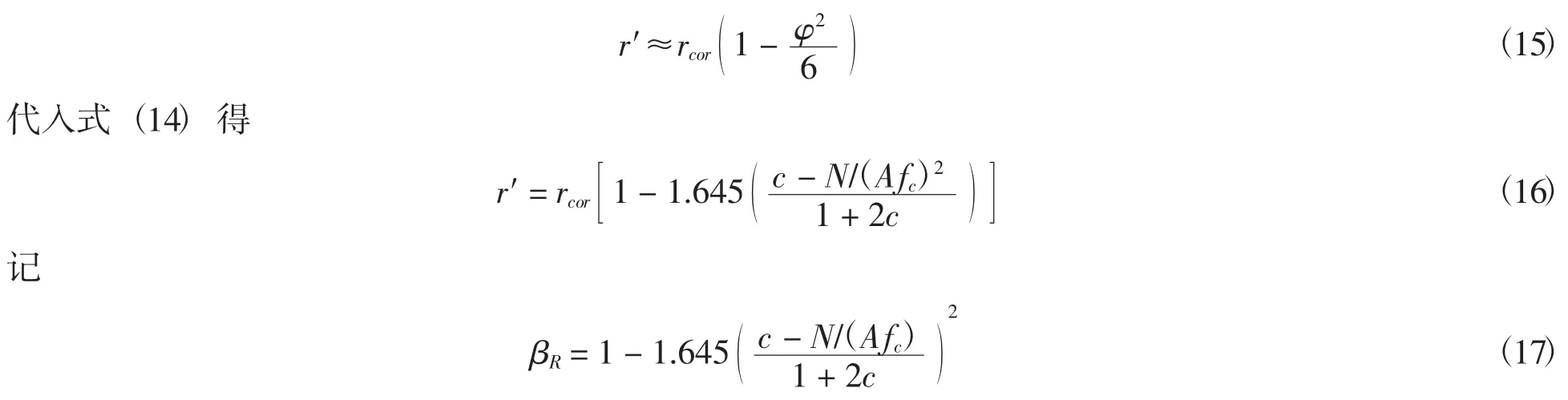
1.5 建立极限承载力表达式

构件破坏时，两侧壁裂缝倾角由公式（7）和公式（8）所得.假定混凝土受压区中心于裂缝最低点正上方，距离圆心r′的位置.

取隔离体为图4破坏面右侧的部分，对混凝土受压区中心所在轴线取矩（图中的1-1轴）.对破坏面列平衡方程，建立极限承载力表达式.

1.5.1 箍筋拉力产生的力矩

对隔离体采用柱坐标，则裂缝上每一点，可由法向量为z轴方向的平面上，其与最低点的张角唯一确定.考虑距最低点张角φ处的箍筋拉力，如图4所示：其力臂L，为箍筋弧线段长与的积θ，拉力F在y方向的投影为因此箍筋拉力产生的力矩为

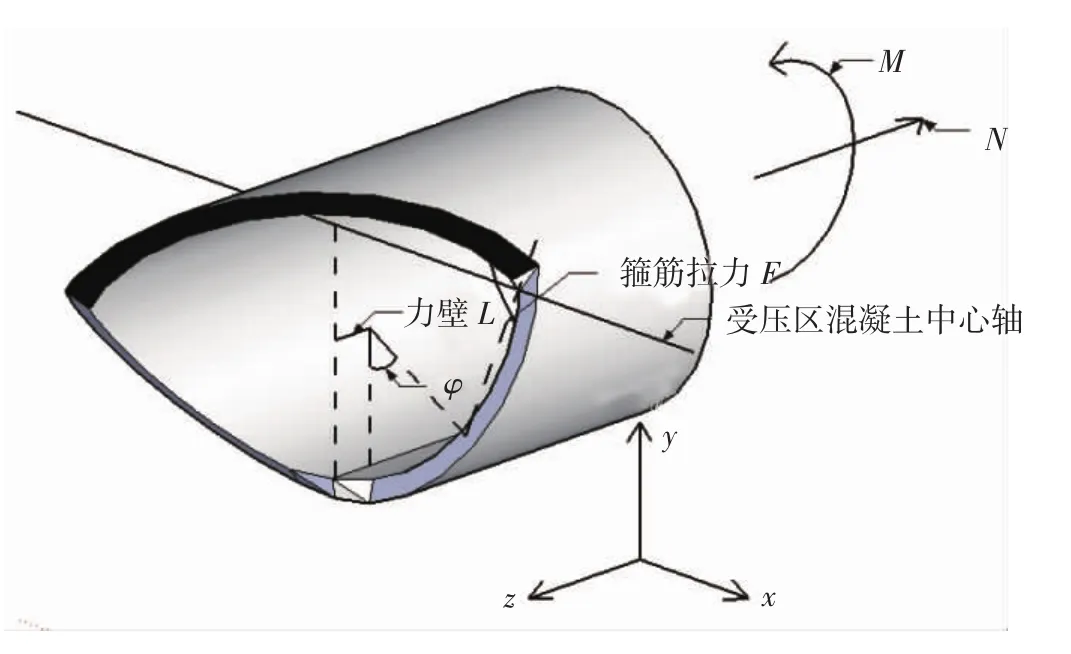
图4 隔离体受力示意图Fig.4 Foces on the free body

1.5.2 纵筋产生的力矩

假定裂缝处纵筋都受拉屈服，受压区纵筋都受压屈服.对受压区中心取矩时，受压区纵筋合力矩为零.则全部纵筋产生的力矩与全纵筋受拉屈服产生的力矩相等，为

1.5.3 外力产生的力矩

将公式（19）、公式（20）代入公式（21）得

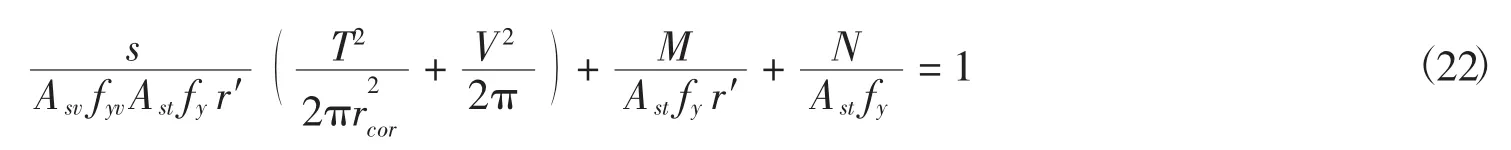
公式可改写为

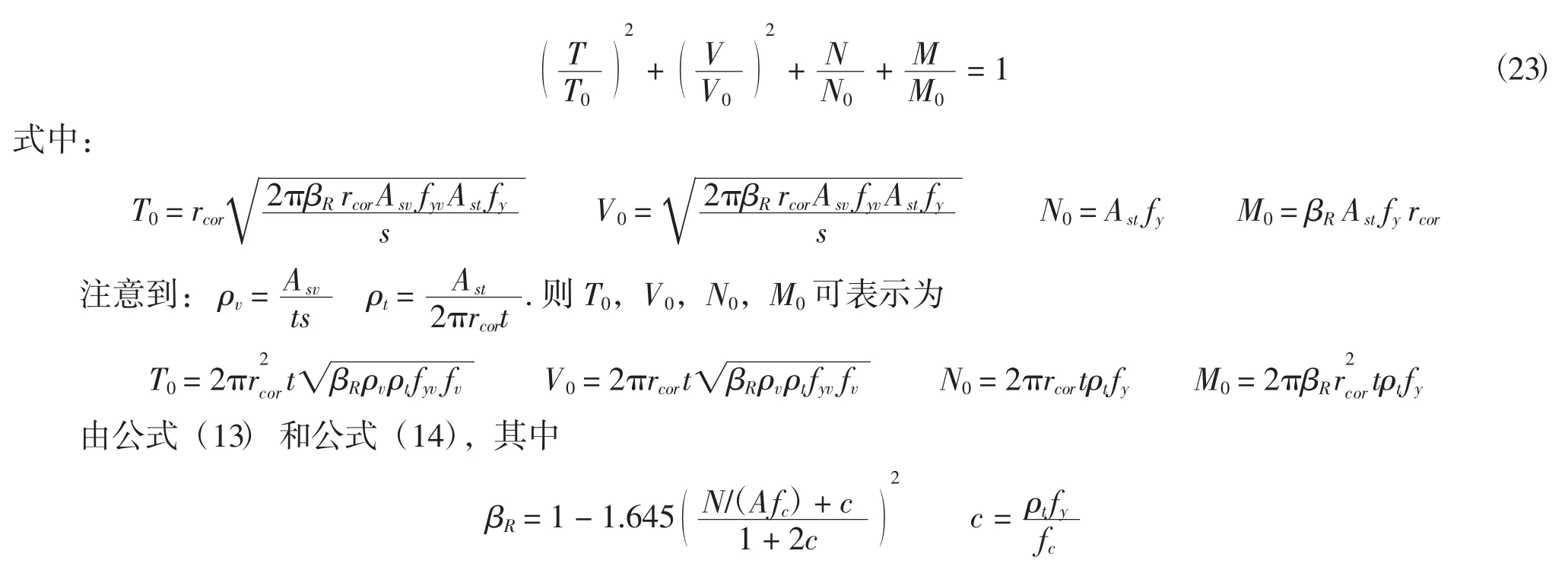
2 试验验证及其他理论对比

关于环形钢筋混凝土构件复合受力极限承载力的统一表达式，国内在这方面的研究还相对欠缺.霍锦峰[5]在其研究中给出与本文近似的理论公式：

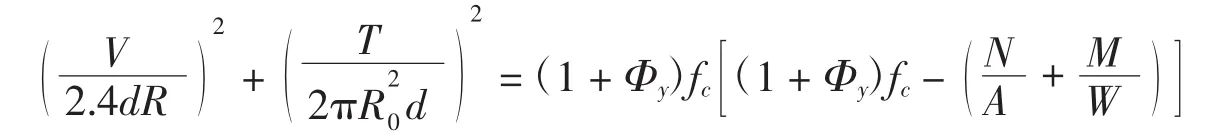
为验证本文模型的可行性，本文选取吕志涛等[11-12]的环形截面构件弯剪破坏试验数据进行计算，结果见表1，并将计算结果与试验结果对比，结果见表2.

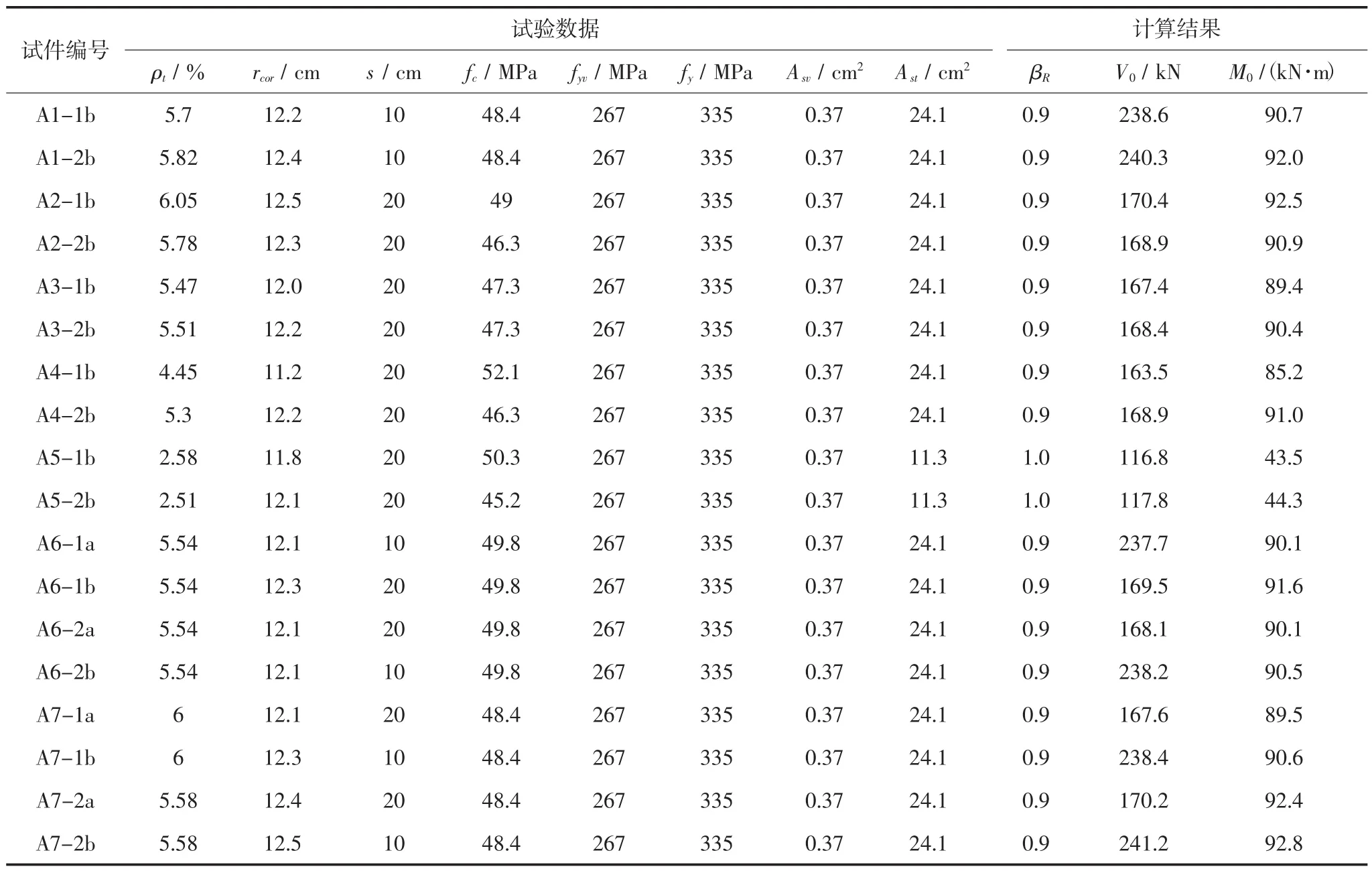
表1 截面构件试验数据与计算结果Tab.1 experimental data for annular section members and calculation results

由表2最后1列值与1的比较，均值1.3，标准差0.21，可见模型能一定程度上反应真实破坏情况.大部分破坏时大于1，可知理论公式偏于安全.

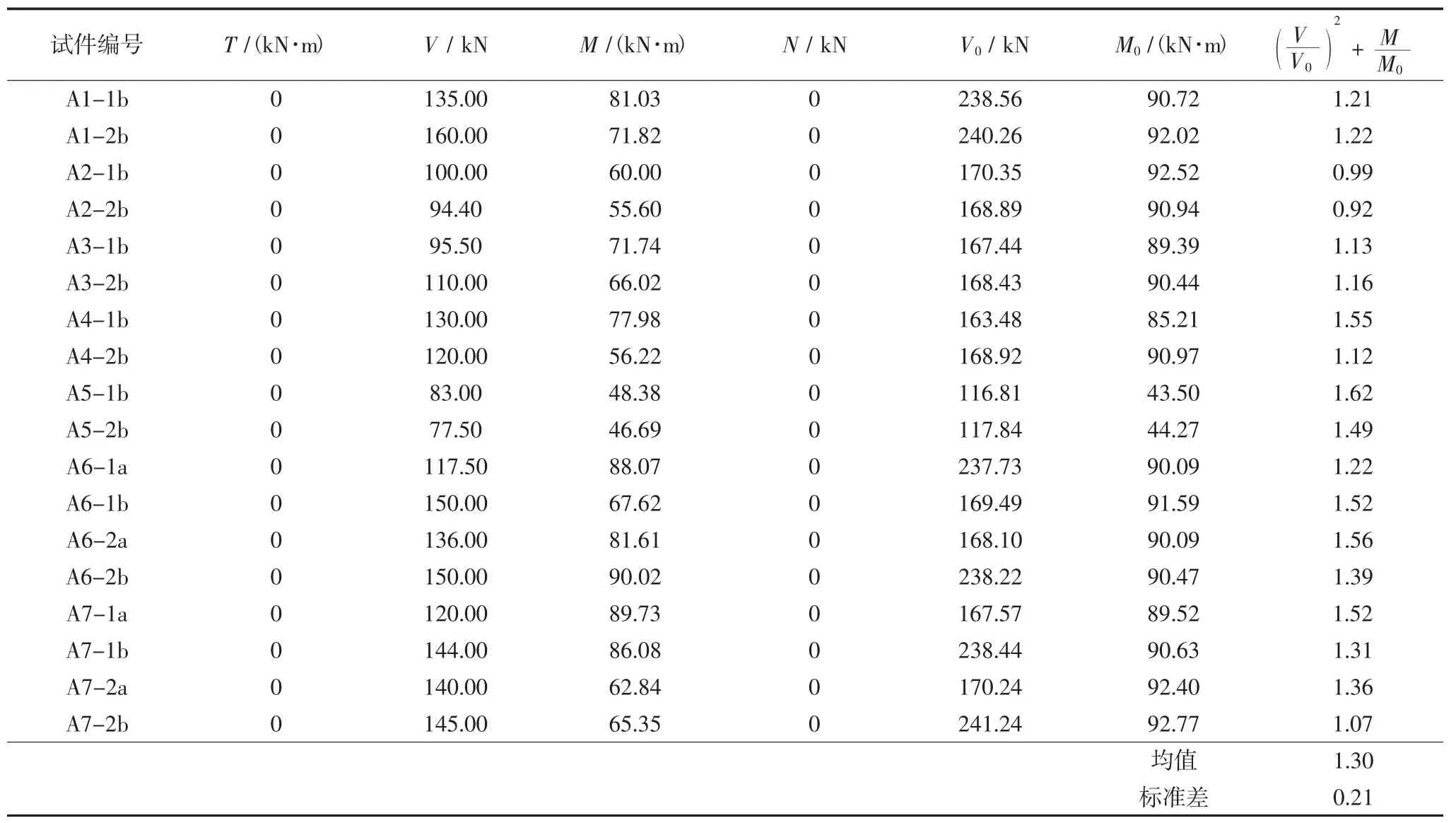
表2 模型解与实验值对比Tab.2 Comparison of medel results to experimental results

3 结论

对于钢筋混凝土环形截面构件复合受力破坏，本文首先通过变角空间桁架理论获得裂缝倾角，随后依据正截面受力平衡计算受压区高度，最后通过建立对混凝土受压区中心轴的力矩平衡，推导出了拉压、弯、剪、扭各种内力组合作用下极限承载力的计算公式.

该计算公式形式简洁，易于计算.与现有的环形截面构件试验结果进行比较，理论公式偏于安全.可以用于在复杂静力荷载作用下钢筋混凝土结构极限承载力的计算.

[1]刘继明.钢筋混凝土复合受扭构件受力行为和设计方法的研究[D].西安：西安建筑科技大学，2004.

[2]HusTTC.Unified approach to shear analysis and design[J].Cement and Concrete Composites.1998，20（6）：419-435.

[3]李宏，刘西拉.混凝土拉、剪临界破坏及纯剪强度[J].工程力学，1992，54（4）：23-29.

[4]HsuTTC.Toward a unified nomenclature for reinforced-concrete theory[J].Engineering Mechanics.1996，122（3）：275-283.

[5]霍锦锋，刘西拉.钢筋混凝土环形截面构件破坏的统一表达[J].上海交通大学学报，2005，39（11）：1866-1869.

[6]骆华勋，刘西拉.钢筋混凝土环形截面构件的统一破坏模型[J].上海交通大学学报，2012，46（1）：152-157.

[7]THOMASTCH.Torsion of Reinforced Concrete[M].Van Nostrand Reinhold Company，Inc，1984.

[8]门进杰，史庆轩，刘继明.钢筋混凝土复合受扭构件抗扭承载力统一方程[J].西安建筑科技大学学报（自然科学版），2006，38（2）：227-231.

[9]林咏梅，周小真，张连德.钢筋混凝土双向压弯构件在单调扭矩作用下抗扭性能的研究[J].建筑结构学报，1996，17（1）：30-39.

[10]刘继明，史庆轩，李志军，等.钢筋混凝土箱型构件双向压弯剪反复扭矩作用的性能研究[J].建筑结构，2007，37（7）：20-24.

[11]吕志涛，周明华，陈友文.环形截面钢筋混凝土受弯构件的抗剪强度实验研究[J].南京工学院学报，1980（3）：26-31.

[12]吕志涛，石平府，周燕勤.圆形、环形截面钢筋混凝土构件抗剪承载力的实验研究[J].建筑结构学报，1995，16（3）：13-20.

[责任编辑 杨屹]

Ultimate bearing capacity of annular section RC members subjected to compound forces

WANG Meng,WANG Pu,HUANG Zhen
(School of Naval Architecture,Ocean and Civel Engineering,Shanghai Jiao Tong University,Shanghai 200240，China)

Base on variable-angle space truss model theory,the ultimate bearing capacity of reinforced concrete members with ring sections subjected to compound forces was studied in this paper,which includes the form of the failure cross section and a practical formula for calculating the ultimate capacity.Firstly,the inclination angle of failure surface was derived base on variable-angle space truss model theory,by which the failure surface was determined.Secondly,equilibrium equations were set-up by the balance of the isolated body besides the failure surface,by which unified expressions to ultimate bearing capacity were built.Finally,theoretical expressions were compared with experiment results.

reinforced concrete;ring-section;compound force;ultimate bearing capacity

TU375

A

1007-2373（2017）02-0099-06

10.14081/j.cnki.hgdxb.2017.02.017

2016-11-23

国家自然科学基金（51178265）

王蒙（1991-），男，硕士研究生，wangsage@sjtu.edu.cn.通讯作者：黄真（1963-），女，教授，zhenhuang@sjtu.edu.cn.