浅谈两个重要极限的应用型教学

□孙芳菲

（陕西国际商贸学院 陕西 咸阳 712046）

浅谈两个重要极限的应用型教学

□孙芳菲

（陕西国际商贸学院 陕西 咸阳 712046）

两个重要极限在高等数学中占着非常重要的位置，不仅是函数求极限的一种方法，而且它的应用思想——凑形式，在以后的教学中将会被广泛应用。本文主要讲述这两个重要极限的推广型与应用性，对于第一个极限的应用（型）在凑形式时要保证变量的一致性和变量趋于零，对于第二个极限的应用（1∞型）在凑形式时要抓两点“：1+”和“互倒”。

重要极限；凑形式；型；1∞型

1 第一个重要极限

此极限公式的推导依据是应用极限存在第一准则——夹逼准则，各类高等数学教材上对于此推导过程都有详细的讲解[1]，故此处不再详述。不过，在此推导过程中出现的相对重要的几个性质应不容忽视。分别是：

而在本篇文章里，主要是详细解说一下此极限公式的推广与应用。

1.1 形式的推广

从上例中不难看出，如果分子中三角函数sin后面的变量形式u(x)与分母的变量形式一致且u(x)→0，可采用变量代换思想转化为第一个重要极限从而求出其结果，即极限形式的推广形为：

上述推广形中一定要保证两点：u(x)的形式一致性、u(x)→0，尤其是最后一个，是一些学生容易忽略的。

1.2 形式的应用

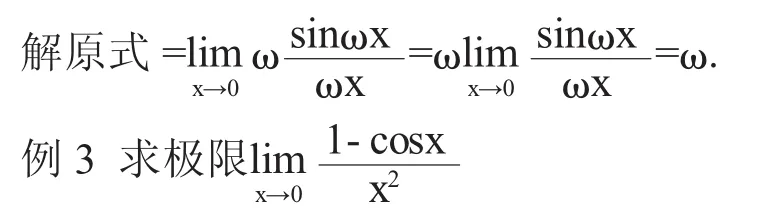
分析：x→0时x2→0，cosx→1,1-cosx→0，故为型且含有三角函数，因此不妨应用半角公式转化为正弦类型，再凑推广形。

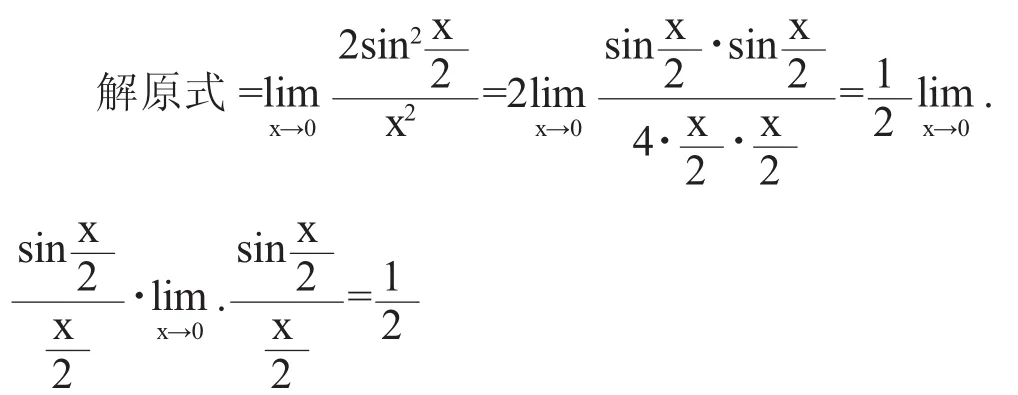
2 第二个重要极限

同样，此极限的推导依据是极限存在准则——单调有界准则[1]，这里也同样不再详述，我们主要关注此极限公式的推广与应用。

2.1 形式的推广

首先，不难看出此极限类型：底数为1+无穷小量，幂次部分为无穷大量，简称1∞型。且底数形式中有“1+”，“1+”后的变量与幂次变量“互倒”，抓住这三点，就不难得出其推广形式。其推广形的抽象概括形式为：

在这里，学生易把此极限类型与其他相似型（如(1+无穷小量）α型）混淆，从而得出结果为1的错误答案，例如（α为任意常数）。总之，对此类极限一定要注意其型，然后根据相应的型来解决。

2.2 形式的应用

分析：为1∞型，在构造推广形时抓两点：“1+”与“互倒”。

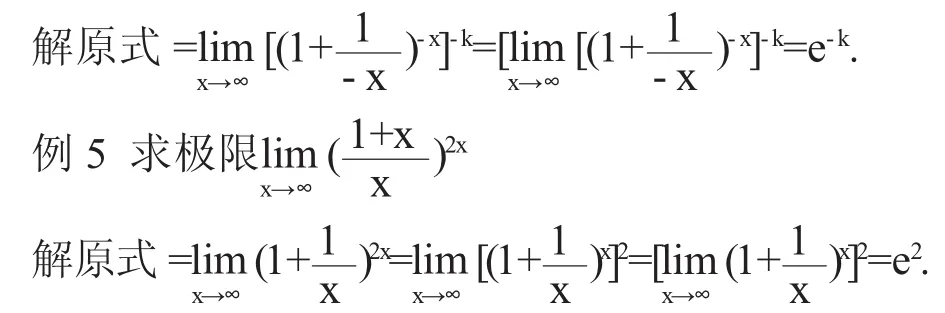
从上面两个例子中可以看出，一旦凑出底数的“1+”和幂次部分满足与底数“1+”后面部分互为倒数，那么此种形式的极限值一定存在，且为自然对数e。而且不难发现，两个例子中最后凑出的最外部幂次部分为常数，利用极限的四则运算就可得到结果。

但是，在实际应用中，不乏会出现最外部幂次部分为函数的形式，此时应该怎么办呢？这里，由函数的连续性我们可得到如下定理：

定理[1]：对于形如u(x)v(x)(u(x)>0,u(x)≠1)的函数（通常称为幂指函数），在同一自变量变化过程中，如果有

通俗来说，对幂指函数求极限，就是对底数和幂次分别求极限。但要注意底数的极限值必须大于零。

总之，无论什么样的形式，只要抓住三点，首先判定是1∞型，在应用第二个重要极限构造凑形式时一定要保证底数部分的“1+”以及幂次和“1+”后面量的“互倒”，然后应用幂指函数求极限或者幂次函数求极限，那么问题就迎刃而解了。

对于两个重要极限的应用，凑形式是很有用的方法，不仅在本文这里，在后面导数的求解、积分的求解中应用性都非常广泛。对于型且含三角类型的，要保证变量一致性和变量趋于零，对于1∞型，要保证底数“1+”和底数和幂次变量“互倒”。

1004-7026（2017）08-0114-02

O13;G642

A

10.16675/j.cnki.cn14-1065/f.2017.08.089