基于蠕变柔量求解沥青混合料连续延迟时间谱*

吕慧杰 刘涵奇 罗 蓉 陈 辉 冯光乐

(武汉理工大学交通学院1) 武汉 430063) (湖北省交通运输厅工程质量监督局2) 武汉 430063)

基于蠕变柔量求解沥青混合料连续延迟时间谱*

吕慧杰1)刘涵奇1)罗 蓉1)陈 辉1)冯光乐2)

(武汉理工大学交通学院1)武汉 430063) (湖北省交通运输厅工程质量监督局2)武汉 430063)

根据AC-13C沥青混合料在5种不同温度下的单轴压缩蠕变试验结果，利用时温等效原理得到沥青混合料的蠕变柔量主曲线；应用蠕变柔量与延迟时间谱之间的数学关系，获得连续延迟时间谱的解析表达式.结果表明，单轴压缩蠕变试验能够获得连续延迟时间谱，然后得到存储柔量.

道路工程；沥青混合料；延迟时间谱；蠕变柔量；主曲线

沥青混合料的线性粘弹性质是对其进行粘弹力学分析以及工程应用的基础.表征沥青混合料基本粘弹性质的物理量包括蠕变柔量、松弛模量、动态模量，以及动态柔量等，这些物理量具有不同的函数表达形式[1-2].根据线性粘弹性原理，这些材料函数都是基于同一延迟时间谱的材料性质的不同体现[3].沥青混合料的延迟时间谱是描述沥青混合料粘弹性与时间或者频率的关系，是各种粘弹函数的核心，通过延迟时间谱可以将各种材料函数联系起来，因此，沥青混合料延迟时间谱的求解对基本粘弹性质的研究有着十分重要的意义.

目前，对于高分子材料、聚合物，以及粘弹性流体等的延迟时间谱研究较多，对于沥青混合料延迟时间谱的研究较少[4].文中将基于单轴压缩蠕变试验，利用时温等效原理，通过绘制蠕变柔量主曲线的方法将较窄的时间域和温度域的蠕变柔量扩展到宽阔的时间域和温度域，然后利用延迟时间谱与蠕变柔量函数的数学关系求解连续延迟时间谱，对延迟时间谱的获取及应用进行探索.

1 延迟时间谱

处于线性粘弹性状态时的沥青混合料，其应力与应变的一维本构关系，可由玻尔兹曼叠加原理进行描述，若输入应力σ(t)，输出应变ε(t)可表示为

(1)

式中：τ为虚拟变量，τ∈[0,t]；D(t)为当沥青混合料处于线性粘弹性状态时的蠕变柔量；σ(t)为输入应力.

目前，沥青混合料的蠕变柔量一般采用由一个弹簧和若干个开尔文元件串联而成的广义开尔文力学模型进行表征，其中弹簧用于表征沥青混合料中的弹性效应，粘壶用于表征沥青混合料中的粘性效应，见图1.图1中E0为瞬时弹性模量；Ei为第i个开尔文元件中弹簧的弹性模量；ηi为第i个开尔文元件中粘壶的粘度；N为开尔文元件的个数.

图1 广义开尔文模型

广义开尔文模型相对应的蠕变柔量Prony级数表达式为

式中：De为平衡柔量，且De=1/E0；Di和ρi分别为第i个延迟强度和延迟时间，且ρi=ηi/Ei.

式(2)中的蠕变柔量定义在一系列离散的延迟时间点ρi上.如果将广义开尔文模型中开尔文元件的个数无限制地增加，离散时间点的间隔将趋近于无限小，ρi将变为连续的时间轴.根据积分的定义，可以将式(2)中的Di替换为F(ρ)dρ，则级数形式的式(2)变为如下积分的形式[5]

(3)

由于沥青混合料的延迟时间经常跨越十几个数量级，所以常常采用自然对数来表示，则式(3)可写为

(4)

式中：L(ρ)为沥青混合料的延迟时间谱.L(ρ)为一种分布函数，L(ρ)d lnρ为延迟时间在lnρ和lnρ+d lnρ之间的对粘弹性材料柔度的贡献.

由式(4)可知，蠕变柔量的函数表达式是一个含有延迟时间谱的积分表达式，即蠕变柔量可以由延迟时间谱表示出来.那么，延迟时间谱也同样可以由一个含有蠕变柔量的解析表达式表示.因此，为了得到延迟时间谱的解析表达式，可以通过单轴压缩蠕变试验先确定蠕变柔量的函数，然后再求解延迟时间谱的解析表达式.

2 试 验

2.1 试验材料

沥青选用SBS改性沥青，集料选用石灰岩.采用AC-13C型沥青混合料，通过试验确定的集料的合成级配见表1，最佳油石比为4.30%.

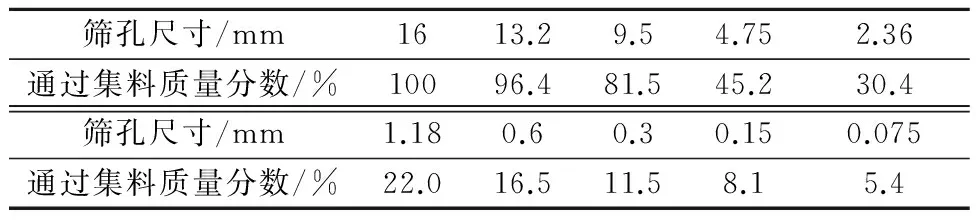
表1 沥青混合料矿料级配组成

根据规范中的有关规定[6]，热拌沥青混合料试件的制备采用Superpave旋转压实试件制备方法，首先成型高度为170 mm、直径为150 mm的圆柱形试件，然后用取心机取心(直径100 mm)，并用切割机切割，得到高度为150 mm、直径为100 mm的试件.通过水中重法测量计算各试件的空隙率，当试件的空隙率满足4.0%±0.5%的要求，且上下表面水平时方可用于单轴压缩蠕变试验.本次试验选用两个合格试件进行平行试验，两个试件分别记作HMA-1和HMA-2.

2.2 单轴压缩蠕变试验

采用多功能材料试验机进行单轴压缩蠕变试验.为了研究沥青混合料在不同温度下的蠕变性质，试验在0,10,20,30,40 ℃五个温度下进行.在每次试验前均将试验试件放置于环境箱中进行养生，养生温度为相对应的试验温度，养生时间不少于3 h，以保证试件的温度与试验温度一致.试验的加载时间为120 s，且为了确保沥青混合料处于线性粘弹性阶段，施加的轴向力需保证试件的累积应变小于150×10-6[7].各温度下均对两个试件进行平行试验，试验结果取两个试件数据的平均值.通过对原始的试验数据进行计算，得到原始的蠕变柔量数据点，AC-13C沥青混合料试件在不同温度下的蠕变柔量随加载时间的分布情况见图2.

图2 各温度下蠕变柔量曲线

由图2可知，沥青混合料的蠕变性能是与温度和加载时间相关的.当温度相同时，蠕变柔量随着加载时间的增长而变大；当加载时间相同时，蠕变柔量随着温度的升高而增大.沥青混合料的蠕变性能对其抗车辙性能有很大的影响，蠕变柔量越大，抗车辙能力越弱.这说明温度的升高和加载时间的增长会降低沥青混合料的抗车辙性能.沥青混合料蠕变性能的时间温度相关性将作为绘制蠕变柔量主曲线的理论基础.

3 求解连续延迟时间谱

根据线性粘弹性理论，延迟时间谱是各种粘弹函数的核心，可以将各种粘弹函数有机结合起来.相关研究表明，通过蠕变柔量函数D(t)可以近似计算连续延迟时间谱，分别通过微商近似求得，并且计算的精度随着微商次数的变高而提高.一般研究中求2次近似得到的L(ρ)已足够精确.文中采用2次近似求解连续延迟时间域，其表达式为

(5)

3.1 绘制蠕变柔量主曲线

单轴压缩蠕变试验的加载时间和试验温度均是有限的，不足以满足工程实践的要求.为了在更广温度和时间范围内研究沥青混合料的蠕变性质，可以通过利用绘制蠕变柔量主曲线的方法实现.沥青混合料是一种典型的粘弹性材料，满足时温等效原理，即以试验温度和参考温度下的蠕变柔量做对比，当试验温度高于参考温度时，该试验温度对参考温度下蠕变柔量的影响相当于在参考温度下延长试验时间，其具体数学表达式为

D(T,t)=D(Tref,tr),tr=t/αT

(6)

式中：T为试验温度；t为试验加载时间；D(T,t)为试验温度和试验加载时间下测得的蠕变柔量；Tref为指定的参考温度；tr为缩减时间；D(Tref,tr)为参考温度和缩减时间下的蠕变柔量；αT为移位因子.

根据时温等效原理，研究采用CAM模型作为主曲线的拟合模型、采用Arrhenius方程作为时温位移因子绘制蠕变柔量主曲线.CAM模型和Arrhenius方程的表达式为

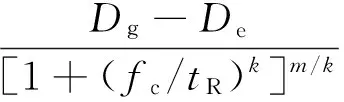
(7)

(8)

式中：De，Dg，fc，m和k均为拟合参数；ΔE为活化能；R为通用气体常数；T和Tref分别为热力学温度标下的试验温度和参考温度.

以20 ℃为参考温度，采用CAM模型和Arrhenius方程，通过EXCEl表格的非线性数据拟合功能对试验数据进行拟合，拟合的目标为式(9)所示误差最小，拟合得到的参数见表2，得到的蠕变柔量主曲线见图3.根据拟合的结果计算拟合优度，其值为0.999 2，说明采用CAM模型和Arrhenius方程可得到与试验数据相符的蠕变柔量主曲线.

(9)

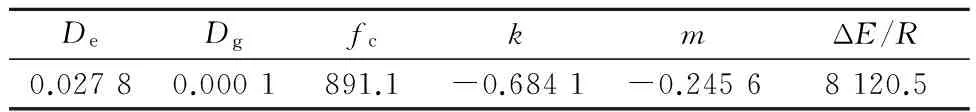
表2 拟合参数

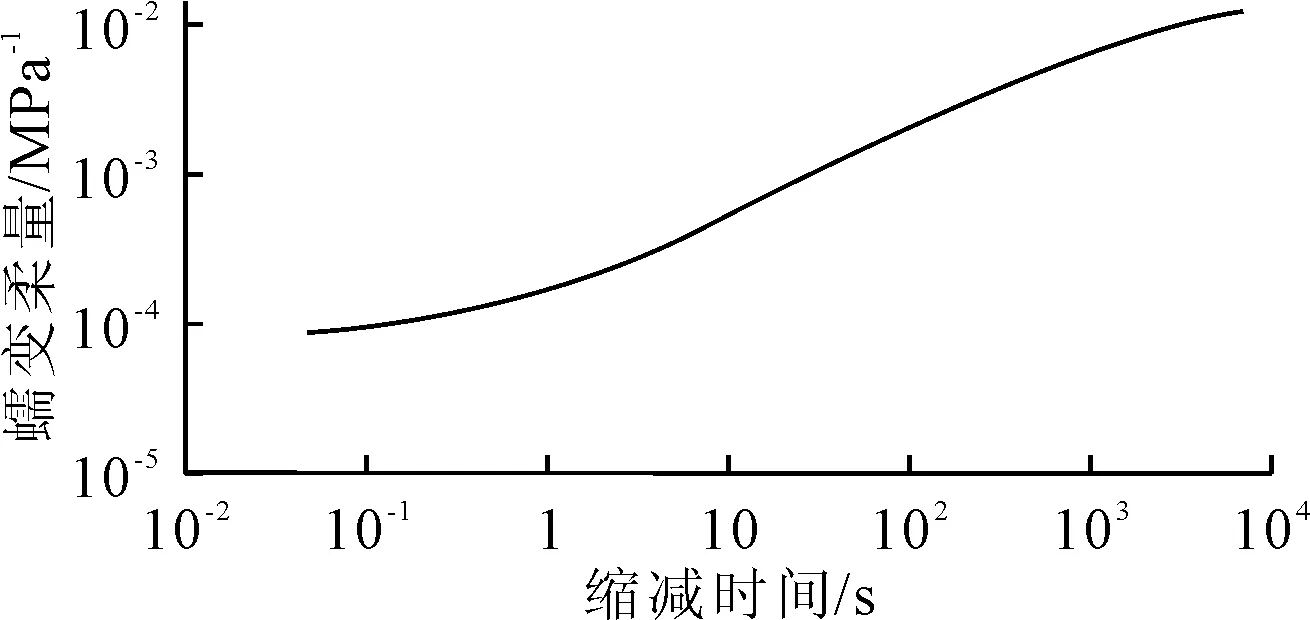
图3 蠕变柔量主曲线(参考温度：20 ℃)

3.2 求解连续延迟时间谱

基于CAM模型的蠕变柔量函数关系式，分别计算蠕变柔量函数的1次和2次微商，然后将计算结果带入式(5)，得到近似的连续延迟时间谱L(ρ)为

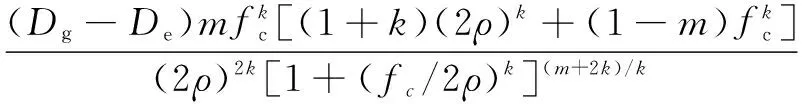
(10)

将表2所列的拟合参数带入式(10)，最终计算得到AC-13C沥青混合料的连续时间谱，其表达式见式(11)，曲线图见图4.

L(ρ)=1.684 6×10-4ρ0.684 1(0.196 6+

0.011 9ρ0.684 1)(1+0.015 4ρ0.684 1)-2.359 0(11)

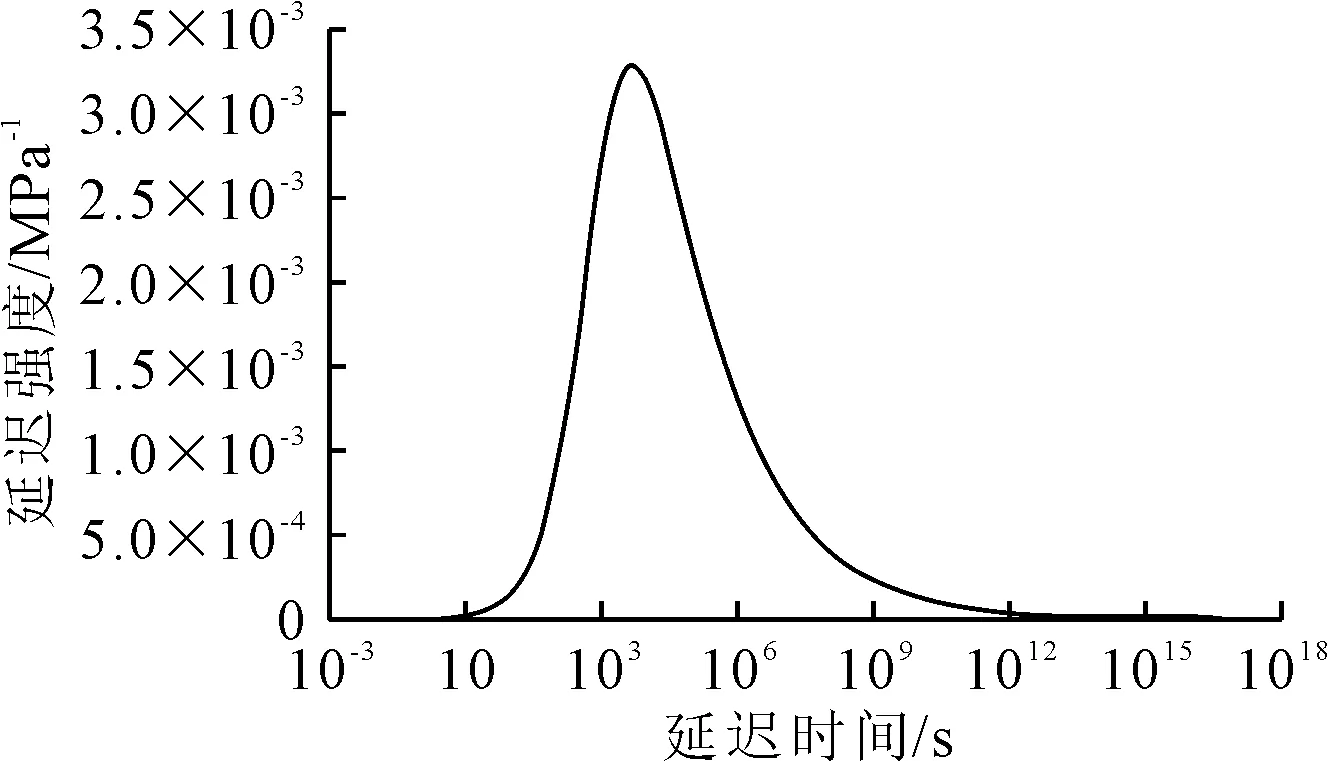
图4 连续延迟时间谱(参考温度：20 ℃)

3.3 连续延迟时间谱的应用

延迟时间谱是各种粘弹函数的核心，可以通过延迟时间谱得到其他粘弹函数.本文以利用延迟时间谱求解储存模量为例加以说明.根据弹性粘弹性对应原理，可得储存柔量的表达式为

(12)

根据定积分的数学含义，则可以将储存模量的积分表达式写为

(Δlnρi=0.5ln 10)

(13)

将表2所列各拟合参数的值带入式(13)中，则可以得到AC-13C沥青混合料试件的存储柔量，其主曲线见图5.

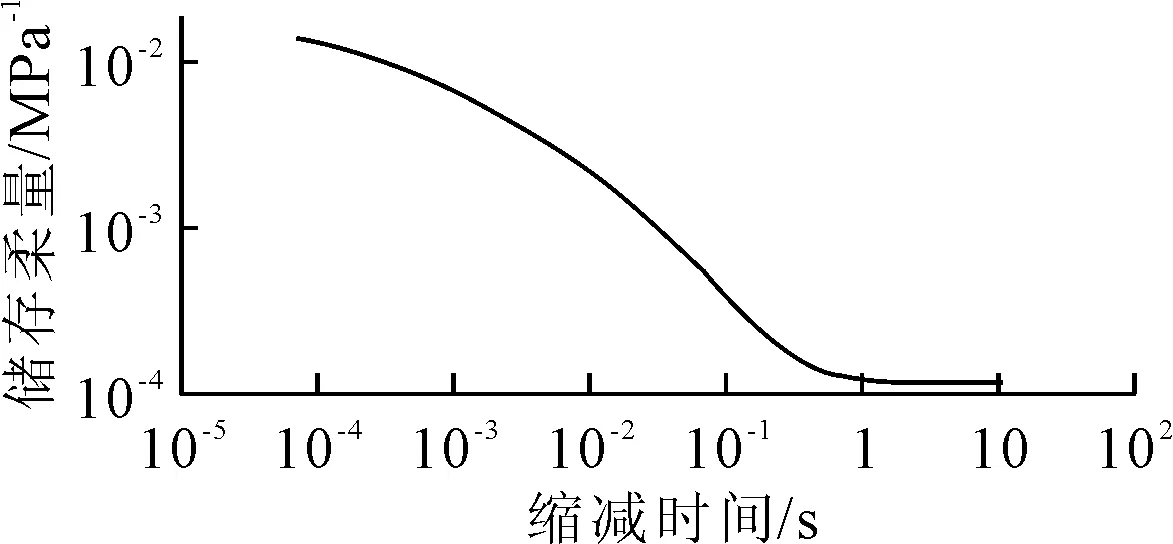
图5 储存柔量主曲线(参考温度：20 ℃)

通常，利用动态试验确定储存柔量主曲线，通常需要在5个试验温度(-10，4.4，21.1，37.8和54.4 ℃)和6个试验频率(0.1，0.5，1，5，10和25Hz)进行交叉试验，一组试验需要约2天的时间，试验的过程耗时较长.通过简单的蠕变试验，利用延迟时间谱获取存储柔量主曲线可以节约大量时间，有利于相关研究的开展.

4 结 论

1) 随着温度的升高和加载时间的增加，沥青混合料的蠕变柔量增大，存储柔量减小，抗车辙能力下降.

2) 基于时温等效原理，利用CAM模型可以很好地确定蠕变柔量的主曲线，用以表征沥青混合料蠕变柔量在较宽时间和温度范围内的变化情况，为实际工程应用提供参考.

3) 基于线性粘弹性理论，通过蠕变柔量求解得到连续的延迟时间谱，并以此为桥梁得到储存柔量主曲线，从而为沥青混合料及路面结构粘弹力学响应分析提供有效途径.

[1]LUO R, LYTTON R L. Characterization of the tensile viscoelastic properties of an undamaged asphalt mixture[J]. Journal of Transportation Engineering,2010,136(3):173-180.

[2]LUO X, LUO R, LYTTON R L. Characterization of fatigue damage in asphalt mixtures using pseudostrain energy[J]. Journal of Materials in Civil Engineering,2012,25(2):208-218.

[3]迟凤霞,张肖宁,邹桂莲.基于动态模量主曲线的沥青混合料连续松弛时间谱[J].华南理工大学学报(自然科学版),2008,36(10):76-80.

[4]赵延庆,王国忠,王志超,等.沥青混合料松弛时间谱分析[J].建筑材料学报,2010,13(5):636-640.

[5]SUN Y, CHEN J, HUANG B. Characterization of asphalt concrete linear viscoelastic behavior utilizing havriliak-negami complex modulus model[J]. Construction & Building Materials,2015,99(1):226-234.

[6]交通运输部公路科学研究院.公路工程沥青及沥青混合料试验规程:JTG E20—2011[S].北京：人民交通出版社,2011.

[7]赵延庆,唐积民,白龙.利用沥青混合料复数模量确定松弛模量研究[J].建筑材料学报,2012,15(4):498-502.

Determination of Continuous Retardation Spectrum of Asphalt Mixtures Based on Creep Compliance

LYU Huijie1)LIU Hanqi1)LUO Rong1)CHEN Hui1)FENG Guangle2)

(School of Transportation, Wuhan University of Technology, Wuhan 430063, China)1)(Division of Engineering Quality Supervision, Department of Transportation of Hubei Province, Wuhan 430063, China)2)

Based on the results of uniaxial compressive creep tests performed on AC-13C asphalt mixtures at five temperatures, the time-temperature superposition principle is employed to generate the creep compliance master curve. The analytical expression of continuous retardation spectrum is then derived with the application of the mathematical relationship between creep compliance and continuous retardation spectrum. The results indicate that: the uniaxial compressive creep tests can obtain the continuous retardation spectrum of asphalt mixture quickly and the resulting continuous retardation spectrum can then be converted to storage modulus.

road engineering; asphalt mixtures; continuous retardation spectrum; creep compliance; master curve

2017-02-23

*国家重点基础研究发展计划(973计划)项目资助(2015CB060100)

U414

10.3963/j.issn.2095-3844.2017.03.027

吕慧杰(1992—)：男，硕士生，主要研究领域为沥青路面材料