基于相位旋转和帧头检测的16APSK相位模糊纠正算法
冯晓文,李庆坤,成亚勇
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
基于相位旋转和帧头检测的16APSK相位模糊纠正算法
冯晓文,李庆坤,成亚勇
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
针对16APSK信号载波同步的多重相位模糊问题,提出了一种简单的结合相位旋转和帧头检测的相位模糊纠正算法。对16APSK信号载波同步的相位模糊问题做了简要介绍,并进行了数学推导和分析。提出的相位模糊纠正算法,首先利用CORDIC算法进行角度计算和相位旋转,把16APSK信号的12重相位模糊降低到4重相位模糊,接着利用帧头检测技术对4重相位模糊进行纠正,最终得到正确的星座图和解码数据。为了验证算法的可行性,在FPGA上对提出的相位模糊纠正算法进行了实现和测试,测试结果表明,提出的算法能够正确纠正16APSK信号载波同步中的多重相位模糊问题。
16APSK调制;相干解调;相位模糊;相位旋转
0 引言
在宽带卫星通信中,由于星际链路较长,为了保证卫星信号的有效传输,调制端的功率放大器常常工作在其饱和点附近[1]。功率放大器固有的非线性会导致调制信号幅度失真和相位失真。由于APSK对非线性失真具有固有的抵抗性,且具有较高的功率有效性和频带利用率,因此是一种非常适合非线性卫星信道的调制方式[2]。16APSK的星座图由内外2个同心圆组成,幅度变化较少,复杂度较低,在卫星通信领域是一个非常有前景的调制方案[3]。
对于信号的解调,一般有相干解调[4]和非相干解调[5]。在相干解调载波同步的相位估计中,普遍存在相位模糊问题。QPSK存在4重相位模糊问题[6],8PSK存在8重相位模糊问题[7],16APSK也存在多重相位模糊问题[8]。一般采用差分编码可以克服相位模糊问题[9],但需要在发射端和接收端分别加入差分编码电路和差分检测电路。另外,对于相干解调系统,差分编码还存在误码扩散问题[10]。本文提出了一种结合相位旋转和帧头检测的方法,可以克服16APSK的多重相位模糊问题。
1 16APSK模型
APSK的星座图由多个包含不同数目信号点的同心圆构成,每个同心圆相当于一个PSK星座图[11],描述如下:
(1)
式中,k=1,2,3,…,K为同心圆的数目;rk为第k个同心圆的半径;nk为第k个同心圆上的信号点数目;ik=0,1,2,…,nk-1;θk为第k个同心圆上信号点的初始相位。16APSK的星座图由2个同心圆构成,研究较多的是4+12形式的16APSK,即内圆有4个信号点,外圆有12个信号点。本文中,16APSK星座图外圆和内圆的半径比为r2/r1=2.7;初始相位分别为θ1=π/4,θ2=π/12,其星座图如图1所示。
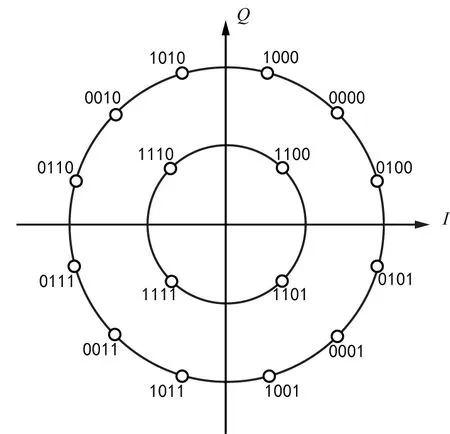
图1 4+12形式的16APSK调制星座图
2 16APSK相位模糊分析
接收机收到16APSK信号后,要进行相干解调。在相干解调算法中,一般采用锁相环来实现载波同步[12]。对于16APSK信号的载波同步,有一些常见的算法,如判决引导算法(DD算法)[13]、极性判决算法[14]和简化星座算法[15]等。简化星座算法由于其同步建立时间较短,环路跟踪稳定的特点,受到广泛欢迎。在简化星座算法中,对16APSK信号执行3次方运算。根据16APSK的星座特点,3次方运算之后,内圆的星座点收缩到接近于0,外圆的星座点扩大,变成一个QPSK星座图[16],如图2所示,这样则可采用QPSK的鉴相算法。
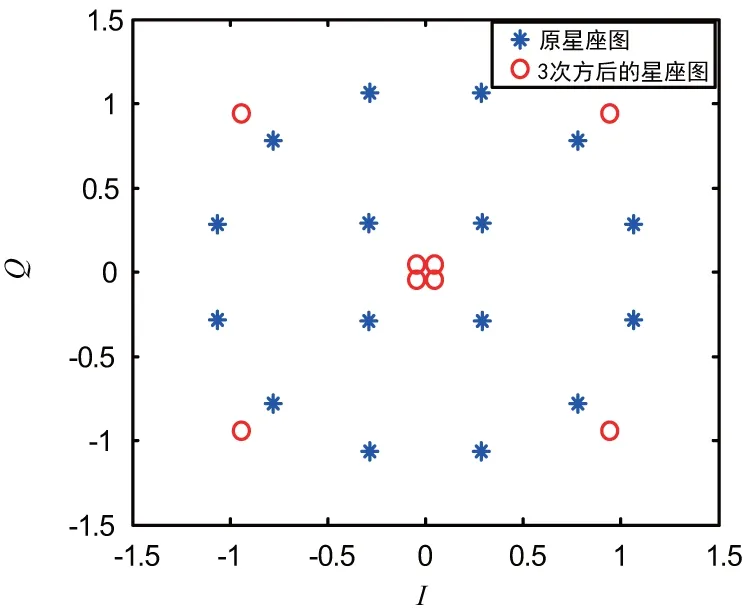
图2 16APSK原星座图和3次方后的星座图
下面对简化星座的载波同步算法进行推导,从而分析16APSK信号的相位模糊问题[17]。假设接收端的本振正交信号为:

(2)
式中,wc为本振频率。接收端收到的16APSK信号为:
y(t)=a(t)cos[wct+θe(t)]+b(t)sin[wct+θe(t)]。
(3)
式中,a(t)和b(t)分别指正交同相分量的值;θe(t)指接收端本振和16APSK信号载波的相差。
接收信号经过下变频处理,再通过低通滤波器滤除倍频分量,得到的正交同相信号为:
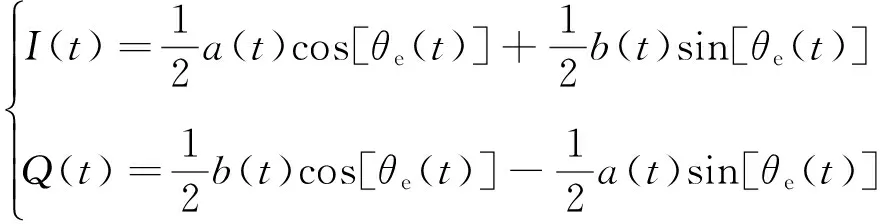
(4)
为了简化推导,式(4)可改写为:
(5)
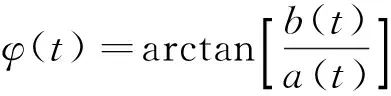
(6)
在简化星座载波同步算法中,对式(6)进行3次方运算,有
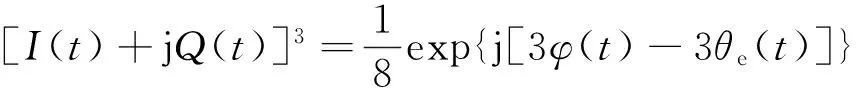
(7)
进行3次方运算后的新的正交同相信号为:

(8)
3次方后的星座图显示,内圆的信号很小,对鉴相误差影响较小,因此主要考虑外圆星座点的鉴相误差。外圆星座点正好是QPSK,则采用QPSK的鉴相算法[18],鉴相公式为:
D[θe(t)]=sgn[Q′(t)]I′(t)-sgn[I′(t)]Q′(t)。
(9)
QPSK存在0,π/2,π或3π/2四重相位模糊,在式(9)简化过程中,假设相位锁定在0相位,即满足条件-π/4<3θe(t)<π/4,当3θe(t)接近于0相位时,有sin[3θe(t)]≈0,cos[3θe(t)]≈1。这样鉴相公式最终可简化为:
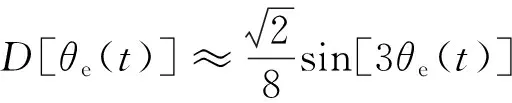
(10)
对于θe(t),在-π/4<3θe(t)<π/4范围内存在3重相位模糊,同理在QPSK另外的3种相位模糊情况下(π/4<3θe(t)<3π/4,3π/4<3θe(t)<5π/4,5π/4<3θe(t)<7π/4),也分别存在3重相位模糊。因此在16APSK的简化星座载波同步算法中,仍存在12重相位模糊。下面针对16APSK的相位模糊问题提出解决方法。
3 16APSK相位模糊纠正算法
本文提出一种简单的纠正16APSK相位模糊问题的算法,该相位模糊纠正算法的原理如图3所示。在完成载波同步和位同步之后,得到的星座图是12重相位模糊情况中的一种。如果直接进行星座映射解码,不能解出正确的数据,必须对星座图进行相位补偿旋转,得到正确的星座图才能解码。本文提出的算法主要包括4个模块:标记内圆星座点模块、偏转角度计算模块、星座图相位补偿旋转模块和帧头检测模块。

图3 相位模糊纠正算法原理
3.1 标记内圆星座点模块
该模块用于从符号流中找到内圆上的星座点,通过和符号模值的平均值比较,符号模值小于平均值的星座点被判定为内圆上的星座点。由于计算符号模值需要开根号运算,在FPGA中开根号的计算比较复杂,因此直接用模值的平方值进行比较。每个符号的模值的平方值标记为:
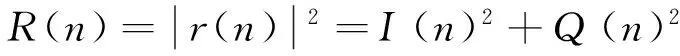
(11)
式中,n为符号的序列号。符号流模值的平方的平均值为:

(12)
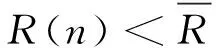
3.2 偏转角度计算模块
内圆上有4个星座点,正好分别分布在4个像限。只需要一个像限的星座点,就可以计算出星座图偏转的角度,在这里采用第一像限的星座点。如果正交同相2路数据的符号都为正,则判定该星座点在第一像限,然后计算该星座点的角度(计算多次第一像限的星座点角度取平均值)。星座点角度的计算采用CORDIC算法[19]的向量模式。CORDIC算法的基本原理如下:

(13)
式中,(x,y)分别为星座点的横坐标I(n)和纵坐标Q(n);α为从星座点(x,y)变换到(x′,y′)旋转的度数。sin(α)和cos(α)的值存储在查找表中。找到的内圆上第一像限的星座点按着如图4所示的方式旋转,直到纵坐标y′为零或者接近于零时停止旋转。

图4 CORDIC算法迭代示意
每次旋转角度的累积就是该星座点的角度。CORDIC算法计算角度的准确度跟其迭代次数有关。迭代次数越多,计算的角度值越准确,但耗费的资源越多。本文中CORDIC算法的迭代次数为10次,计算的角度精度为0.09°。
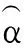
3.3 星座图相位补偿旋转模块
3.4 帧头检测模块
经过前面3个模块的运算,获得的星座图可以进行星座映射解码。但因为图1的星座度旋转0,π/2,π或3π/2不会发生变化,所以仍存在4重相位模糊。可以对4种可能的星座图进行并行解码,然后对解码后的数据进行帧头检测,出现正确帧头的数据即为相位模糊纠正正确的数据。假设帧头设置为“EB90”,则另外3种相位模糊情况的帧头分别为“C671”、“D8A3”和“F542”。只有检测到“EB90”帧头的数据才是最后解码正确的数据。
4 FPGA硬件平台验证
为了验证提出的相位模糊纠正算法,在FPGA上进行了实现和测试。
测试信号为16APSK调制信号,采样频率为56 MHz,载波频率为70 MHz。载波同步采用简化星座算法[16],位同步采用Gardner算法[20]。用QuartusII自带的嵌入式逻辑分析仪SignalTap II Logic Analyzer采集载波同步和位同步完成之后的数据,再导入到Matlab软件中,得到如图5所示的星座图。从图5中可以看出,锁相环锁定的星座图存在相位模糊。
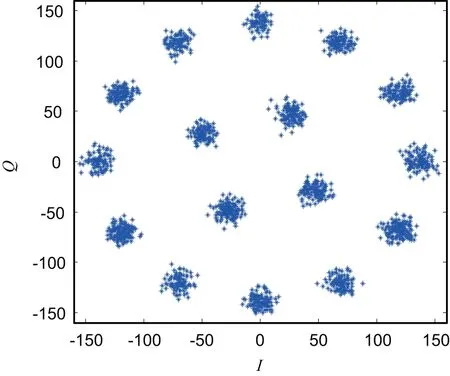
图5 载波同步和位同步后的星座图
根据内圆上第一像限星座点的角度算出修正星座图所需旋转的度数为π/12(在FPGA中用341表示,因为在FPGA中角度查找表大小为8 192,即一个周期2π分成8 192份)。获得旋转所需的角度后,星座图按照式(13)进行旋转,获得修正的星座图如图6所示。
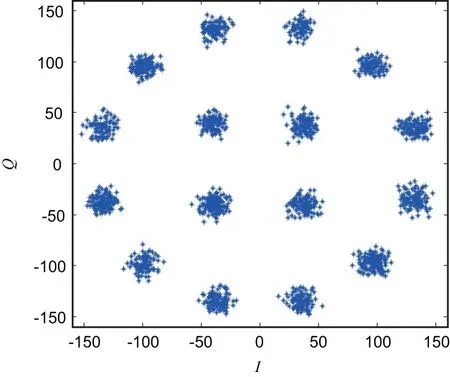
图6 相位补偿旋转后的星座图
对旋转后的星座图进行映射解码,因为仍存在4重相位模糊,所以对0,π/2,π或3π/2四种模糊度的星座进行并行解码,用嵌入式逻辑分析仪采集到的数据如图7所示。在程序中设置“EB90”为帧头,从图7中可以看出,4种可能的解码数据帧头分别为“EB90”、“F542”、“D8A3”和“C671”。选择帧头为“EB90”的数据作为最后的解码数据输出。

图7 帧头检测模块仿真数据
5 结束语
本文提出了一种结合相位旋转和帧头检测的16APSK信号相位模糊纠正算法。该算法利用内圆星座点的位置计算出修正星座图所需的角度,采用CORDIC算法进行相位旋转,得到修正的星座图。修正的星座图仍存在4重相位模糊,再利用帧头检测的方法对剩余的4重相位模糊进行纠正,最终得到正确的解码数据。算法原理简单,易于在硬件平台上实现。在FGPA上的测试结果表明,提出的算法能够成功地纠正16APSK的12重相位模糊问题,验证了算法的可行性。该算法在低信噪比的情况下,由于受到噪声的干扰,可能会出现内圆星座点角度计算不准确的情况。在下一步的工作中,还需进一步研究低信噪比条件下纠正相位模糊的问题。
[1] 郭雅琴,叶焱,刘太君,等.逆F类功放数字预失真改进算法[J].无线电通信技术,2014,40(5):61-64.
[2] 雷菁,黄英,刘志新.非线性卫星信道中APSK信号星座优化设计研究[J].武汉理工大学学报,2006,28(8):117-121.
[3] 崔霞霞,江会娟,万明刚.一种8PSK、16APSK与32APSK软解映射的实现技术[J].无线电工程,2011,41(4):45-48.[4] 耿虎军.高速数字相干解调的研究[D].西安:西安电子科技大学,2010.
[5] 王伟,张靖,王伟伟.FSK信号非相干解调的数字实现[J].无线电通信技术,2010,36(4):61-64.
[6] 郭兴阳,谢德芳.QPSK数字化解调相位模糊校正方法研究[J].空军工程大学学报(自然科学版),2001,2(1):41-44.
[7] 何军,郭勇.PTCM+8PSK克服相位模糊技术的FPGA实现[J].无线电通信技术,2014,40(1):90-92.
[8] 何朝玉,李超,陈晖,等.一种适用于突发16APSK信号的载波同步算法[J].无线电工程,2012,42(5):61-64.
[9] 崔颖.差分编码关键技术研究[D].北京:北京邮电大学,2013.
[10] 王岳,熊蔚明.基于独特码检测的载波相位模糊纠正方法[J].现代电子技术,2009(3):62-64.
[11] 宫晓妍,刘建伟,杨友福.基于卫星信道的APSK调制研究[J].遥测遥控,2009,30(6):10-14.
[12] 潘申富,王立功.全数字时钟锁相环的设计[J].无线电通信技术,2002,28(4):49-50.
[13] LI J,FENG D Z,ZHENG W X.An Efficient Soft Decision-Directed Algorithm for Blind Equalization of 4-QAM Systems[C]∥2016 IEEE International Symposium on Circuits and Systems(ISCAS),2016:1 726-1 729.
[14] 夏文娟,窦建华,刘洋,等.高阶QAM的载波恢复方法研究[J].合肥工业大学学报(自然科学版),2013,36(6):700-703.
[15] 李湘鲁,代涛,姚远程.基于FPGA的16APSK数字接收机的设计与实现[J].电子技术应用,2013,39(3):47-49.
[16] 徐烽,邱乐德,王宇.基于精简星座鉴相的大频偏16-APSK信号载波同步[J].电子技术应用,2012,38(12):87-90.
[17] 徐烽,邱乐德,王宇.16-APSK信号NDA鉴相新算法[J].电讯技术,2012,52(10):1 614-1 618.
[18] 黄凌.基于FPGA的QPSK全数字调制解调系统的设计与实现[D].南京:南京航空航天大学,2010.
[19] 黄海.基于CORDIC的离散三角变换快速算法及其实现研究[D].哈尔滨:哈尔滨工业大学,2014.
[20] 李建海,成亚勇.QPSK调制解调中的Gardner定时恢复算法研究与性能分析[J].无线电工程,2004,34(10):55-57.
An Algorithm of Phase Ambiguity Correction for 16APSK Based on Phase Rotation and Frame Header Detection
FENG Xiao-wen,LI Qing-kun,CHENG Ya-yong
(The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)
A simple phase ambiguity correction algorithm combining phase rotation and frame header detection is proposed for resolving the multiple phase ambiguity problem of 16APSK signal carrier synchronization.The phase ambiguity problem of 16APSK signal carrier synchronization is briefly introduced,and the mathematical derivation and analysis are carried out.For the proposed algorithm,firstly the phase ambiguity of 16APSK signal is reduced from 12-fold to 4-fold depending on the angle calculation and phase rotation calculated by CORDIC algorithm,then the 4-fold phase ambiguity is corrected by the header detection technique,finally the corrected constellation diagram and decoded data are obtained.In order to verify the feasibility of the proposed algorithm,it is implemented and tested on FPGA.The test results show that the proposed algorithm can correctly resolve the multiple phase ambiguity problem of 16APSK signal carrier synchronization.
16APSK modulation;coherent demodulation;phase ambiguity;phase rotation
10.3969/j.issn.1003-3106.2017.07.04
冯晓文,李庆坤,成亚勇.基于相位旋转和帧头检测的16APSK相位模糊纠正算法[J].无线电工程,2017,47(7):15-19.[FENG Xiaowen,LI Qingkun,Cheng Yayong.An Algorithm of Phase Ambiguity Correction for 16APSK Based on Phase Rotation and Frame Header Detection[J].Radio Engineering,2017,47(7):15-19.]
2017-02-20
国家高技术研究发展计划(“863”计划)基金资助项目(2013AA122904)。
TN911
A
1003-3106(2017)07-0015-05
冯晓文 男,(1986—),博士,工程师。主要研究方向:航天测控。
李庆坤 男,(1976—),博士,高级工程师。主要研究方向:航天测控。

