最小二乘法压差传感器原位校准

褚福刚，杨全海，乔文生，康 宁，韩 用

(中国航天科工集团第六研究院601所，内蒙古 呼和浩特 010076)

最小二乘法压差传感器原位校准

褚福刚，杨全海，乔文生，康 宁，韩 用

(中国航天科工集团第六研究院601所，内蒙古 呼和浩特 010076)

针对喷管摆动试验中压差传感器输出数据处理较复杂，导致摆动力矩计算不准确的问题，开展了压差传感器原位校准技术研究，并采用最小二乘法对校准数据进行处理，修正了压差传感器输出数据的处理公式，提高了喷管摆动力矩计算精度。阐述了压差传感器原位校准方法及最小二乘法在压差传感器校准中的应用，与原有公式计算结果相比，校准后压差传感器输出数据计算精度提高了56.88%。

校准；数据处理；最小二乘法；压差传感器

0 引言

喷管摆动过程中，喷管力矩的大小会对推力向量控制产生重要影响[1]，是摆动试验的主要测试项目。目前通常采用电液伺服作动器控制喷管进行摆动[2]，因而摆动力矩的计算精度主要受作动器输出的力矩数据处理精度影响。由文献[3-4]可知，由于喷管摆动试验的特殊性，喷管摆动试验现场工作环境与作动器出厂检验环境有很大不同，采用出厂设定的力矩数据处理公式对实际试验数据进行处理，往往具有较大误差。根据文献[5-6]可分析得出，数据处理误差产生原因主要包括力矩数据的零位误差和作动器的力矩转换系数误差2个方面，二者都与试验现场的试验环境有关。因此需要对作动器力矩输出进行试验现场原位校准，得出准确的力矩数据处理计算方法，提高喷管摆动试验的力矩计算精度[7]。此外，对作动器进行原位校准后，其力矩测量值与喷管现场实际摆动力矩更加一致，因此是喷管摆动虚拟试验的重要现场数据来源，对实现虚拟现实一致性方面具有重要作用[8]。

理论上，压差传感器校准数据应具有较好的线性，但在校准时难免引入信号噪声和测量误差，使校准数据偏离其理论直线[9]，因此需要对压差传感器校准数据进行处理和分析，推算出真实的数据处理公式。最小二乘法是一种数学优化算法，根据文献[10-11]可知，它通过最小化误差的平方和寻找数据间的最佳匹配函数，可有效用于曲线拟合，并使得到的曲线与实际曲线之间的误差平方和最小。因此提出采用最小二乘法对压差传感器校准数据进行曲线拟合，以快速有效地得出真实的压差传感器计算公式。

1 压差传感器校准

目前电液伺服作动器通常采用压差传感器测量压差信号，测试中喷管摆动力矩的计算依据是压差传感器的输出信号，由于该信号易受试验现场环境影响，而文献[12-13]通过原位校准能够将环境因素校准到传感器输出数据中，因此需要对压差传感器输出数据处理公式进行原位校准。由于影响到喷管力矩计算公式精度的因素主要包括压差传感器输出零位和压差与电压之间的线性公式，其中压差传感器的输出零位需要在对作动器供压之前，分别记录压差传感器的输出值，因此建立压差与电压之间的转换公式是进行压差传感器计算公式原位校准的重点。建立的喷管力矩原位校准系统简图如图1所示，其中PL是控制腔压差传感器，长线缆传输距离与实际试验距离相同。

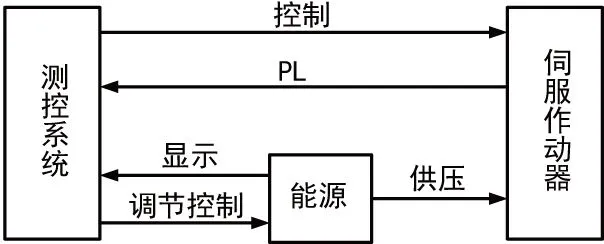
图1 压差传感器原位校准系统

在压差传感器原位校准系统中，测控系统远距离对伺服作动器进行摆动控制和压差采集，对液压能源进行控制调节并读取压力值，液压能源按调节的压力值对作动器提供压力。原位校准原理是对伺服作动器供固定数值的压力，同时读取采集到的PL电压值，通过提供一系列连续的压力值和采集到的相对应压差传感器输出值，建立压差和压差传感器输出之间的关系公式，其中将传感器输出的零位作为关系曲线的截距。通过上述校准原理便可建立压差传感器的压差和电压之间转换系数，用其对原始压差数据处理公式进行修正，以获取较精确的喷管摆动力矩。由文献[14-15]可知，压差传感器原位校准必须在空载情况下进行，对作动器的控制信号幅值应超过其能达到的最大伸长长度或缩短长度，以使能源压力全部加压到压差传感器上，此时读取的压差压力就是控制输出的能源压力。

2 最小二乘法应用

最小二乘法能够拟合出2列数据间的最佳关系公式，因此对压差传感器原位校准数据进行处理时，采用最小二乘法对压差压力和电压之间的线性关系进行拟合。设定好的一系列压差压力PLij(i=1,2,…,n;j=1,2,…,k)之后，通过采集系统采集到相对应的传感器输出电压Vij(i=1,2,…,n;j=1,2,…,k)，其中n为循环次数，k为采样点数。

设压差压力与电压的真实关系为：

PLn=bV+a,

(1)

则压差测量值与真实值的差值为φ=PLij-PLn，因此建立最小二乘法的优化判据为：

φ=∑(PLij-PLn)。

(2)

将式(1)代入式(2)，得

φ=∑(PLij-a-bVij)2。

(3)

当∑(PLij-a-bVij)最小时，得到的a和b即为校准出的压差压力和电压的关系曲线系数，对a和b求偏导数，并令其等于零，可得

∑2(a+bVij-PLij)=0，

(4)

∑2Vij(a+bVij-PLij)=0。

(5)

由式(4)和式(5)求得a和b两个未知数，得出

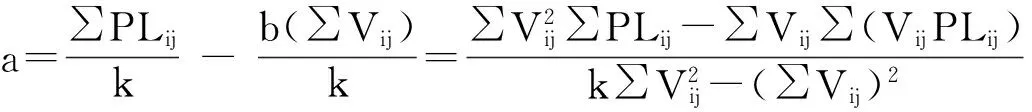
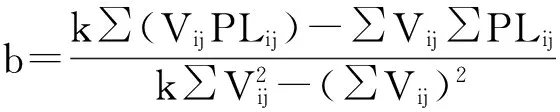
(6)

将式(6)代入式(1)得到的数学模型，便是通过最小二乘法得出的压差压力与电压的关系式，在压力为零时对应的电压便是压差传感器的零位输出。因此，该关系式同时校准了压差传感器零位输出和压差压力与电压之间的转换系数，并使得校准数据与真实值的差值平方和最小[16]。

3 压差校准数据处理

应用伺服作动器推动喷管摆动过程中，采用所提的压差传感器校准方案对数据处理公式进行原位校准，根据文献[17-18]的校准要求，控制液压能源分别对伺服作动器提供0、4、8、12、16和20 MPa的压力，进行6个点的原位校准，共进行了5次校准循环。得到的校准数据共包括6个点的压差压力值和对应的压差传感器输出值，采用最小二乘法对压差传感器的电压与压差压力关系曲线进行拟合。某次校准过程中采集到的压差压力值和对应的PL电压值如表1所示，采用最小二乘法拟合出的直线和采样点分布对比如图2所示。

通过最小二乘法拟合出的压差传感器压力值与压差测量值的直线方程为y=(x-0.097 5)/0.193 3。观察压差传感器测量值和校准得出的直线方程分布图看出，实际测量值紧密均匀分布在校准直线周围。因此，得到的校准直线方程成功拟合了实际测量数据曲线。

表1 压差校准原始数据

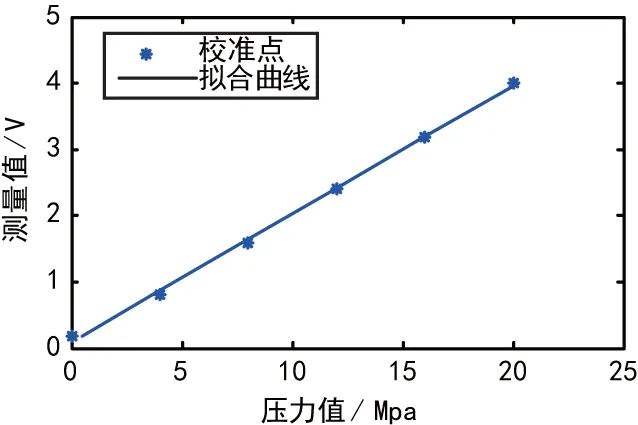
图2 压差校准拟合曲线

压差传感器压力值与测量值的出厂计算公式为y= 5x-0.3，在压力分别为0、4、8、12、16和20 MPa下，对出厂计算结果和校准结果进行比较，比较结果如表2所示。

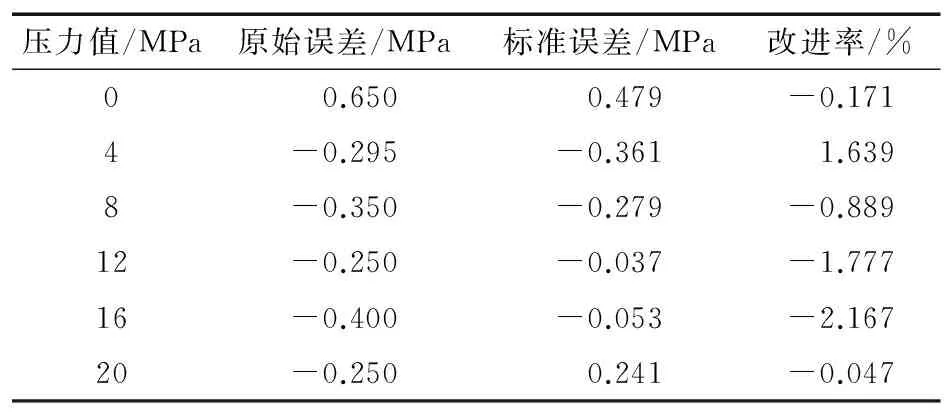
表2 校准结果与原始结果对比

表2中原始误差为传感器出厂计算结果与伺服作动器实际加压值的差值，校准误差为原位校准后计算结果与伺服作动器实际加压值的差值，改进率为校准误差绝对值与原始误差绝对值的差值再与伺服作动器加压值的比值的百分比。观察改进率可以发现，在0、8、12、16和20 MPa压力值下校准后压差传感器误差均小于原始误差，最大偏小比例为2.167%；仅在4 MPa压力值下校准后误差大于原始误差，且偏大值仅为1.639%，因此表明校准效果较为明显。通过对6个点压力值下的压差传感器实测值和计算值比较可以发现，压差传感器校准后数据计算精度比原始计算精度平均提高56.88%。

4 结束语

在喷管摆动试验中，为降低试验现场环境对力矩信号处理产生的影响，提出了一种喷管力矩原位校准方案，用以降低力矩零位和力矩转换系数两方面的误差。其中对力矩转换系数的校准数据进行处理时，采用最小二乘法拟合出了最终的力矩转换系数。对比校准后的力矩转换系数和原始转换系数的转换结果表明，在6个压力值的计算中，校准后的力矩转换结果中5个转换值优于原始转换结果，仅在4 MPa下误差略大于原始转换值，平均转换精度提高56.88%，证明了所采用原位校准方案的有效性较好。

[1] 王春光,史宏斌,王雪坤,等.高压下喷管柔性接头摆动力矩数值分析[J].推进技术,2011,32(2):202-219.

[2] 戴莹,肖丹,刘凤江,等.电液伺服机构装调批生产管理研究与应用[J].航天工业管理,2016(9):39-41.

[3] 李连强,林新兵,曹雄,等.固体火箭发动机地面静止试验的危害及安全防护[J].四川兵工学报,2013,34(4):66-69.

[4] 商霖,廖选平,李璞.固体火箭发动机地面热试车试验研究[J].强度与环境,2015(6):36-44.

[5] 许益民.电液伺服阀动态相频特性CAT数据处理误差分析[J].机械工程学报,2005,41(1):46-49.

[6] 徐峰,张少博,徐海峰.发动机热试车数据测量误差分析及处理方法[J].火箭推进,2012,38(4):72-75.

[7] 郝瑞参，李德才，刘华刚,等.磁流体的性质对压差传感器输出性能的影响[J].仪表技术与传感器，2014(8):16-29.

[8] 邹宇,宫秀良,程博,等.固体火箭发动机虚拟试验技术初探和应用[J].计算机测量与控制,2015,23(8):2 749-2 752.

[9] 张钟华.现代计量测试技术的进展[J].中国计量学报,2006,17(1):1-7.

[10] 贾小勇,徐传胜,白欣.最小二乘法的创立及其思想方法[J].西北大学学报(自然科学版)，2006,36(3):507-511.[11] 张晓安,何晓峰,逯亮清,等.载波相位模糊度递推最小二乘逼近算法[J].无线电工程,2010,2(40)：28-31.

[12] 张学成,荆风林,任敏,等.火箭发动机推力测量的原位自动校准[J].宇航计测技术,1998,18(2):60-64.

[13] 读德方,赵国荣,周建军.总体最小二乘法在惯导原位标定中的应用[J].电光与控制,2011,18(4):89-92.

[14] 杨文荣,王菲，刘剑飞,等.磁性液体微压差传感器校准信号源的研究[J].仪器仪表学报,2011,32(4):801-806.

[15] 杨军,范静,李程.非线性电感式压差传感器动态校准[J].计量、测试与校准,2011,3(5):15-18.

[16] 田垅,刘宗田.最小二乘法分段直线拟合[J].计算机科学,2012,39(6):482-484.

[17] 赵楠,武伟,刘昕.一种基于信号幅度测量的相位校准方法分析[J].无线电工程,2010,40(9):62-64.

[18] 王丽红,王玲.基于VEE的信号发生器自动校准系统[J].无线电工程,2010,40(2):51-64.

In-situ Calibration of Differential Pressure Sensor Based on Least Square Method

CHU Fu-gang,YANG Quan-hai,QIAO Wen-sheng,KANG Ning,HAN Yong

(TheSixthResearchInstituteofChinaAerospaceScienceandIndustryCorporation,HohhotInnerMongolia010076,China)

Considering the swing moment calculation inaccuracy due to the complex data processing of differential pressure sensor in nozzle swing test,the in-situ calibration technique of differential pressure sensor is studied.The least square method is used for the processing of calibration data,the processing formula of sensor output data is modified,and the accuracy of nozzle swing torque is improved.The paper describes the method of in-situ calibration of a differential pressure sensor as well as the application of least square method in calibration.As compared with the previous calculated result,the calculation accuracy of the differential pressure sensor output data after calibration is improved by 56.88%.

calibration;data processing;least square method;differential pressure sensor

10.3969/j.issn.1003-3106.2017.07.18

褚福刚,杨全海,乔文生,等.最小二乘法压差传感器原位校准[J].无线电工程,2017,47(7):75-77.[CHU Fugang,YANG Quanhai,QIAO Wensheng,et al.In-situ Calibration of Differential Pressure Sensor Based on Least Square Method[J].Radio Engineering,2017,47(7):75-77.]

2017-02-20

国防基础科研基金资助项目。

�

A

1003-3106(2017)07-0075-03

褚福刚 男，(1983—)，硕士，工程师。主要研究方向：推力向量测控。

杨全海 男，(1982—)，硕士，工程师。主要研究方向：推力向量测控。