RLS、VSSLMS算法应用于天线组阵的分析及仿真

赵晓明，陈学军，魏瑞利，王青松，苏新军

(西安卫星测控中心，陕西 西安 710043)

RLS、VSSLMS算法应用于天线组阵的分析及仿真

赵晓明，陈学军，魏瑞利，王青松，苏新军

(西安卫星测控中心，陕西 西安 710043)

针对天线组阵常用相关算法Simple、Sumple、Eigen(基于本征值)和LS(最小二乘法)的不足，提出递推式最小二乘法(RLS)和变步长最小均方法(VSSLMS)这2种新型算法，对其应用于深空网天线组阵进行了研究。对这2种算法进行了仿真，结果表明，RLS算法存在信噪比合成性能随组阵天线数目增加而下降的缺陷，VSSLMS算法具有强信号时信噪比合成性能迅速提高的优点；在接收信号弱并且组阵天线数目较少情况下，RLS算法的信噪比合成性能略好于VSSLMS算法；当接收信号较强尤其是组阵天线数目较多时，VSSLMS算法的信噪比合成性能反而比RLS算法更好一些。

天线组阵；信噪比合成性能；递推式最小二乘算法；变步长最小均方算法

0 引言

深空探测是当今航天技术发展的一个重要方向，其主要技术难题之一是微弱信号条件下的信号接收问题，基于性价比及使用灵活性等方面的考虑[1]，将一定数量的天线进行组阵不失为提高微弱信号接收信噪比的有效途径。

当前天线组阵技术的研究方向主要有宽带合成技术、相关算法、天线布局优化、大气环境影响、非均匀阵合成及故障天线的检测和处理等[2]。文献[3-4]对下行宽带信号合成方案、相关算法及合成效率等进行了相关理论分析和初步工程验证，文献[5-6]对天线布局优化问题进行了理论分析和仿真，文献[7]给出了天线组阵中大气扰动的模型，经数值模拟后对扰动造成的增益合成损失进行了评估，文献[8-9]中将均匀天线阵中的一些理论方法推广到非均匀天线阵。针对基于Sumple算法的组阵天线，文献[10]给出了一种权值幅度修正算法，可明显降低故障天线的权值幅度并有助于检测出故障天线。

相关算法的合理选择对提高天线阵信噪比合成性能有着重要的意义，信噪比合成因子(表征信噪比合成损失的大小)或合成效率是评判算法优劣的主要尺度。

深空网天线组阵常用的信号相关合成算法有Simple、Sumple、Eigen和LS[1]。

Simple算法中，指定天线阵中的某一个天线作为参考天线，其余天线的信号分别与参考天线的信号进行相关，再用各个相关结果分别去修正对应天线的信号，使各个天线的信号与参考天线相位对齐，最后将所有天线的信号相加，从而提高SNR。这种算法适用于天线阵中有一个大口径主力天线的情形，选择主力天线作为参考天线可提高相位对齐的程度。严格来讲，此算法不是一种迭代算法，递推次数的增加并不能提高相位对齐精度。

Sumple算法中，作为阵相位参考的不是某一个天线，而是所有其他天线信号的加权和。由于参考是流转参考，因此存在相位漂移[3]。它是一种迭代算法，经不到10次迭代，权系数便趋于收敛。这种算法可适用于比Simple算法更弱的情形。文献[11-12]中对Sumple算法的权值计算及Sumple的相位漂移问题进行了理论分析和数学推导，文献[13]中将Sumple算法相位补偿及信号强度估计方法推广到了非均匀天线阵。

Eigen算法是基于求矩阵本征值的一类算法，文献[14-15]对它的迭代型算法Power Method(幂方法)和Matrix Free Power Method(无需构造相关矩阵的幂方法)进行了介绍。文献[16]针对小区域天线组阵提出了一种基于归一化权的Matrix Free Power Method。文献[17]在SIMULINK仿真平台上对该算法与Simple算法和Sumple算法的合成效率进行了比较。这类算法对噪声较敏感。

LS算法是利用最小均方误差准则得到的一种算法。一般情况下，需要构造相关矩阵并且要求矩阵的逆，运算量大。

上述4种算法中，LS算法的信噪比合成性能最好[1]。但对普通的LS算法而言，在实际应用中可能遇到的困境是：当相关矩阵对应的行列式很小时，最小二乘估计的性能很差；另外，当根据旧的数据构造好相关矩阵后，随着新的数据的产生，必须重新构造相关矩阵，这会面临计算上的困难。

为提高相关合成算法的信噪比合成性能，专家和学者们进行了许多研究。文献[18]中为更精确估计Sumple算法和Simple算法中相位差变化率，给出了一种最小二乘估计与滤波方法。针对信噪比及调制方式未知情况下的天线组阵文献[19]提出了一种权值盲估计算法。文献[20]中针对极低接收信噪比的情形提出了一种基于信噪比估计和单纯形最优化搜索的合成新算法。针对频率选择性衰落信道特性，文献[21]中给出了一种基于频域分量合并的算法。

这里提出2种新型递推算法，RLS算法(递推式最小二乘法)和VSSLMS算法(变步长最小均方法)，它们本质上都是基于最小均方误差准则，因此可以获得很好的信噪比合成性能，同时它们都不需要构造相关矩阵，也不需求矩阵的逆，故相较于LS算法有计算上的优势。RLS算法是最小二乘法的递推表示形式[22]。VSSLMS算法是在LMS(最小均方)算法基础上发展而来的。LMS算法是Widrow和Hoff等人于1960年提出的，它具有结构简单、运算量小、稳定性好的优点，因而得到广泛的应用。LMS算法存在收敛速度和稳态误差这一对固有矛盾，VSSLMS(变步长最小均方)算法可以克服这一矛盾。

探索RLS和VSSLMS算法在天线组阵中的应用，对它们的信号相关合成性能进行仿真和评估颇有意义。

1 深空网天线组阵中的RLS算法

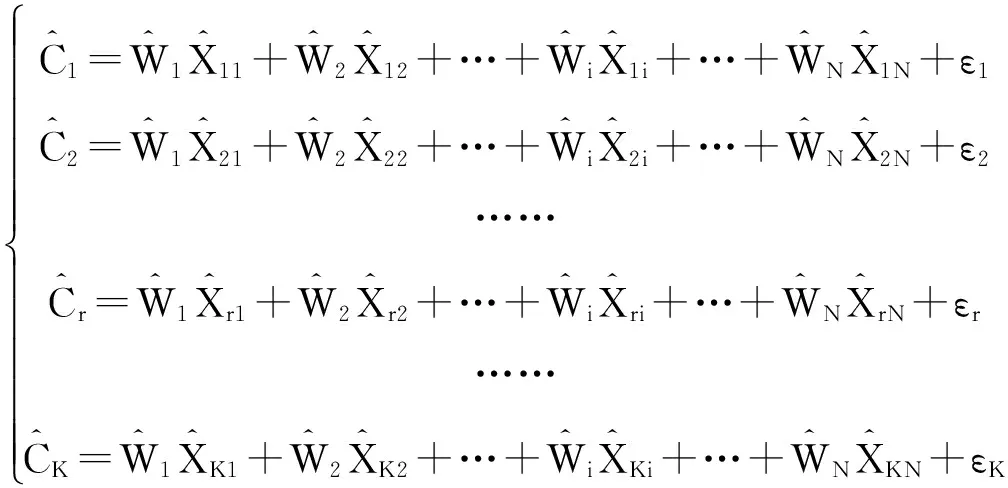
将上述方程组改写为：

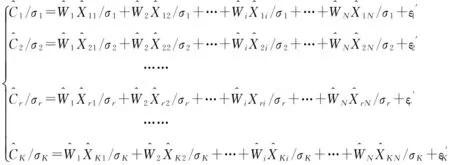
设

则上式可写成矩阵形式：

C=XW+ε。

现定义列矢量b，其中br=(Cr/σr)，定义矩阵A，其中Ari=Xri/σr，则

χ2=(b-AW)T(b-AW)。

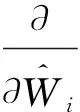
结果为:

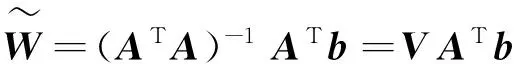
理论上可证明，当σi=σ=常数时，LS算法的实际合成输出的信噪比SNR相对理想合成的信噪比SNR0的合成因子为[7]:

编制好年度财务预算是确保全年经营指标任务完成的基本保障。编制财务预算时，横向先由各部门做好业务预算，比如销售预算、生产预算等，最后由财务部门汇总编制符合企业的财务全面预算。纵向由各分、子公司做好财务预算并由上级单位审核批准后实施，同时上报集团公司并由集团公司编制财务预算，形成全覆盖的预算管理准体系，使财务预算更有针对性和有效性。各企业在编制财务预算的同时，要突出预算的科学性，保持预算的连续性，促进财务预算的编制程序更趋标准，同时要兼顾预算的个性差异，保证预算的顺利实施。

即LS的信噪比合成性能随着递推次数的增加而提高、随着天线数目的增加而下降。

LS的递推算法RLS的表示形式为[23]:

其中，

β为常数；I为单位矩阵。β的取值不影响最终的求解结果，只对递推次数有影响。

2 深空网天线组阵中的VSSLMS算法

LMS算法是基于最小均方误差准则和最陡下降法原理得到的一种递推算法，具有与RLS算法类似的特点，不需构造相关矩阵，也不涉及矩阵求逆。

通常的固定步长LMS算法的迭代公式可表示为：

e(n)=d(n)-XT(n)W(n)，

W(n+1)=W(n)+2μe(n)X(n)。式中，X(n)为时刻n的输入信号矢量；W(n)和W(n+1)分别是时刻n和n+1的加权系数；d(n)为期望输出值；e(n)为误差；μ为恒定步长因子。步长因子μ控制收敛速度且直接影响稳态误差。然而收敛速度和稳态误差是一对固有矛盾，为使收敛速度加快必需提高μ，然而较大的μ却会导致较大的稳态误差，反之较小的μ虽然会减小稳态误差却会导致收敛速度变慢。为了克服这一矛盾，提出了各种变步长LMS算法即VSSLMS，这些变步长算法的共同点是初始阶段使用较大的步长以加快收敛，而在算法收敛后保持很小的步长以获得较小的稳态误差。

VSSLMS算法的关键是构建步长函数，步长函数必须具有如下特点：单调增函数、有界函数和良好的鲁棒性。这里给出4种步长函数[24]：

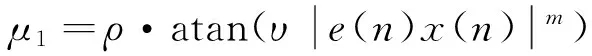
μ2=ρ·(1-exp(-υ|e(n)x(n)|m))，

μ3=ρ·(1-2/(exp(υ|e(n)x(n)|m)+1))，

μ4=ρ·(1-1/(υ|e(n)x(n)|m+1))。

当x≥0时(即图中的e(n)x(n)≥0)，这4种函数都是有界单调增函数；当x=0时，其值为零；x=时，其值为ρ，参数ρ、υ和m分别可调整最大步长值、x较大时步长增加速度及x=0附近步长值的变化的平坦度，因此具有良好的鲁棒性。VSSLMS步长函数特性如图1所示。

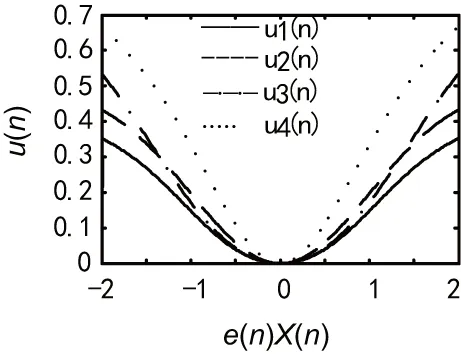
(a) μ1：ρ=1/π，υ=0.5，m=2 μ2：ρ=0.5，υ=0.5，m=2μ3：ρ=0.7，υ=0.5，m=2 μ4：ρ=0.9，υ=0.5，m=2

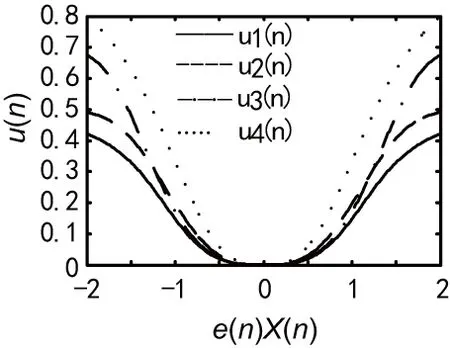
(b) μ1、μ2、μ3和μ4：m=3，ρ和υ同(a)

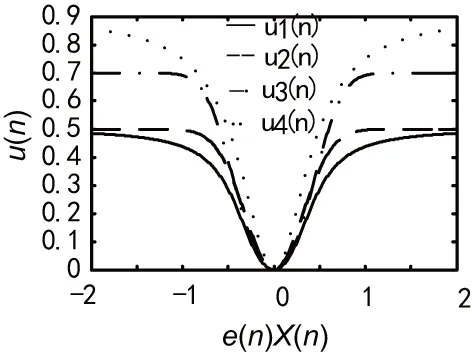
(d) μ1、μ2、μ3、μ4：υ=5，ρ和m同(a)

图1(b)相较于图1(a)，m由2增大到3，|e(n)·x(n)|=0附近曲线变得更加平坦；

图1(c)相较于图1(a)，ρ增大到2倍，μ值也放大到2倍；

图1(d)相较于图1(a)，υ增大到原来的10倍，μ值上升到最大值的速度大大加快。

对天线组阵应用来说还必须考虑相位对齐，因此必须应用复数LMS算法，它的表示式为[25]：

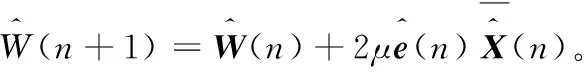
3 RLS和VSSLMS算法的仿真

为简化问题，仿真假设使用的深空网天线阵为等口径天线阵。RLS算法中，取参数β=1 000。VSSLMS算法选用的步长函数为：

μ2=ρ(1-exp(-υ|e(n)x(n)|m))。

取参数ρ=1、υ=10和m=1。

RLS和VSSLMS算法的仿真从信噪比合成因子与单个天线信号信噪比的关系、与阵天线个数的关系及收敛过程3个方面进行，结果如图2所示。

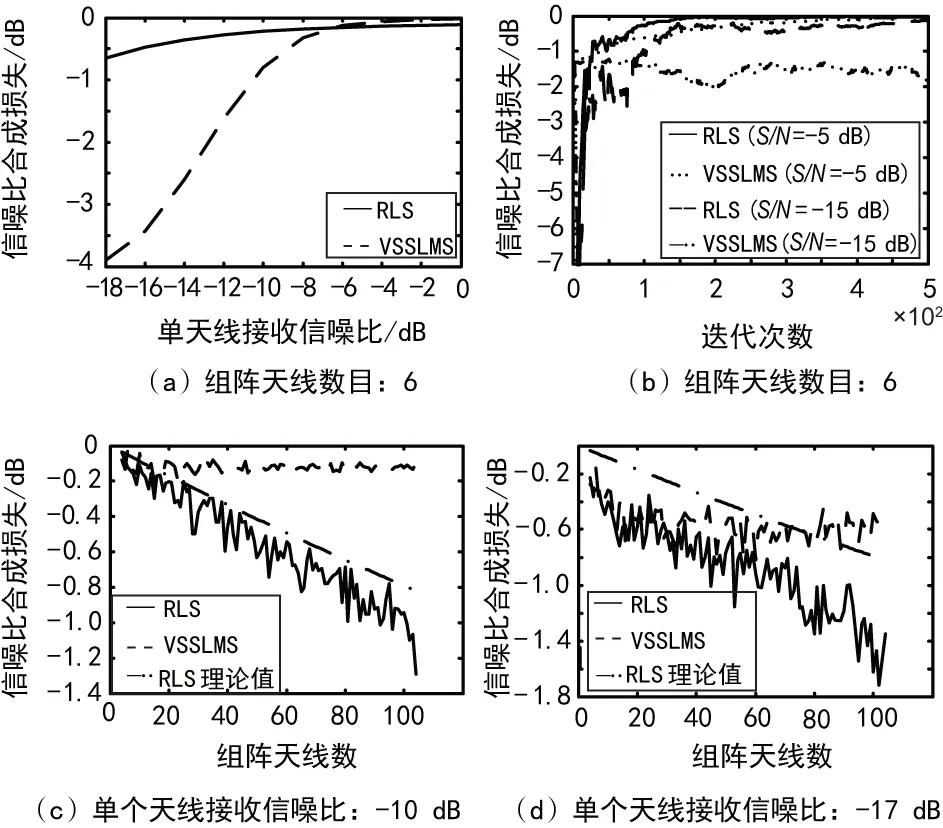
图2 RLS和VSSLMS的信噪比合成因子

由图2(a)可见，RLS算法的信噪比合成性能总体上略好于VSSLMS算法。2种算法的信噪比合成因子都随单个天线信噪比的增加而增加，相比较而言，递推式RLS算法变化得较为缓慢，而VSSLMS算法变化得更快一些；另外，在弱信噪比时，RLS算法的合成信噪比略优于VSSLMS算法，但当信噪比较强时VSSLMS算法的合成信噪比反而更好一些。

图2(b)是2种算法的收敛过程，可以看出，RLS算法收敛得略为快一些，同时可再次看出强、弱信噪比下2种算法的信噪比合成性能特点。

图2(c)和图2(d)是2种算法下信噪比合成因子随组阵天线个数的变化规律。可以看出RLS算法的信噪比合成因子随组阵天线个数的增加而变差，而VSSLMS算法的信噪比合成因子与组阵天线个数无关，当信号较强且组阵天线数目较多时，VSSLMS算法的信噪比合成性能更好。

4 结束语

在深空网天线组阵中应用RLS算法和VSSLMS算法均能在获得很好的合成信噪比的同时避免矩阵计算，大大降低运算量。通过对RLS算法和VSSLMS算法的仿真比较可知：RLS算法存在信噪比合成性能随阵天线数目增加而下降的缺陷，VSSLMS算法的信噪比合成性能与阵天线数目无关；RLS算法的信噪比合成性能随着信号的增强缓慢增加，VSSLMS算法的信噪比合成性能随信号的增强迅速提高；当信号较弱且组阵天线数目不多时，RLS算法的信噪比合成性能略好于VSSLMS算法；当信号较强尤其是阵天线数目较多时，VSSLMS算法的信噪比合成性能比RLS算法更好。

针对工程实际，对RLS和VSSLMS算法在极低接收信噪比及非均匀口径天线阵下的应用今后有必要进行更深入的研究。

[1] ROGSTAD D H.深空网的天线组阵技术[M] .李海涛，译.北京:清华大学出版社，2005．

[2] 徐茂格,柴霖.我国深空天线组阵技术现状与发展思考[J].电讯技术，2014，54(1):109-114．

[3] 钟晓玲，周三文，李海涛，等.天线组阵信号合成技术的研究[J].遥测遥控，2007，28(增)：43-45.

[4] 孟帏,刘莹,张娅楠.下行宽带信号天线组阵试验验证及分析[J].无线电工程，2014，44(9)：28-31．

[5] JONES D L.Geometric Configuration Constraints for Large Deep Space Network Arrays[R/OL].IPN Progress Report,2004:42-157.http:∥tmo.jpl.nasa.gov/ipn_progress_report/ipn.cfm

[6] 徐茂格.深空大规模天线组阵布局设计[J].飞行器测控学报，2013,32(1):7-10．

[7] 党宏杰,史学书,袁嗣杰,等.大气湍流对深空天线组阵影响的仿真分析[J].计算机工程与应用，2010，46(9S):357-360．

[8] 涂启辉,沈彩耀,于宏毅,等.一种非均匀天线组阵下信号时延最优化补偿方法[J].科学技术与工程，2014,14(23):214-218．

[9] 孔德庆.非均匀天线组阵Sumple权值信噪比及信号合成性能分析[J].宇航学报，2009，30(5):1 941-1 945．

[10] 沈彩耀,胡赟鹏,于宏毅.天线组阵中基于Sumple算法的故障天线分析[J].宇航学报，2011，32(11):2 445-2 449．

[11] ROGSTAD D H.The SUMPLE Algorithm for Aligning Arrays of Receiving Radio Antennas:Coherence Achieved with Less Hardware and Lower Combining Loss[R/OL].IPN Progress Report 42-162,August 15,2005.http:∥tmo.jpl.nasa.gov/ipn_progress_report/ipn.cfm

[12] 沈彩耀,于宏毅.天线组阵中SUMPLE算法的合成相位漂移补偿[J].飞行器测控学报，2011，30(6):42-45．

[13] 孔德庆，施浒立.非均匀天线组阵SUMPLE合成相位补偿及信号强度估计[J].电波科学学报，2009，24(4)：632-636．

[14]PERRY Bill.POWER METHOD[OL].Online Linear Algebra Book-Chapter 6,2007.http:∥distance-ed.math.tamu.edu/Math640/chapter6.

[15] LEE C H,VILNROTTER V,SATORIUS E,et al.Large-Array Signal Processing for Deep-Space Applications[R/OL] IPN Progress Report 42-150,August 15,2002.http:∥tmo.jpl.nasa.gov/ipn_progress_report/ipn.cfm

[16] 赵晓明,冯恩信,姜家持.一种用于深空网天线组阵的基于归一化权的Matrix-free Power Method[J].遥测遥控，2009，30(4):15-20．

[17] 赵晓明，偶小娟，陈学军，等．深空天线组阵相关合成算法的Simulink仿真与分析[J]．电讯技术，2015，55(5):509-515．

[18] 孔德庆,施浒立.天线组阵中相位差的递推最小二乘估计与滤波[J].宇航学报，2010，31(1):211-216．

[19] 沈彩耀,于宏毅,顾宇巍,等.一种用于天线组阵的合成权值盲估计算法[J].计算机应用研究，2010，27(10)：3 747-3 749．

[20] 张儒源,詹亚锋,陆建华.基于信噪比估计的天线组阵迭代信号合成新算法[C]∥中国宇航学会深空探测技术专业委员会第八届学术年会论文集：491-495．

[21] 涂启辉,沈彩耀,于宏毅,等.基于频域分量最大比合成的多天线信号合成算法性能分析[J].信息工程大学学报， 2015，16(2):179-182．

[22] RICHTER P.H.Estimating Errors in Least-Squares Fitting[R].TDA Progress Report,1995:42-122.

[23] 郭金吉，甘泉，陈务深．多重线性回归的最小二乘估计的递推算法[J]．南京工业大学学报，2005，27(2)：43-46．

[24] 吴波，李庆梅，刘树东．新的变步长LMS算法及DSP设计[OL]．21IC中国电子网，2010． http:∥www.21ic.com/app/embed/201005/59262.html

[25] WIDROW Bernard,MCCOOL John,BALL Michael.The Complex LMS Algorithm[OL].Proceedings Letters.http:∥www-isl.stanford.edu/people/widrow/papers/j1975thecomplex.pdf.

Analysis and Simulation for RLS and VSSLMS used in Antenna Arraying

ZHAO Xiao-ming,CHEN Xue-jun,WEI Rui-li,WANG Qing-song,SU Xin-jun

(Xi’anSatelliteControlCenter,Xi’anShaanxi710043,China)

For the defects of the four algorithms,Simple,Sumple,Eigen(Eigen value based) and LS(least squares),which are used generally in DSN antenna arraying,two new algorithms,RLS(recursive least squares) and VSSLMS(variable step size least mean squares) are brought forward.And their applications in DSN antenna arraying are discussed and analyzed.Simulations of the two algorithms applied to DSN antenna arraying are performed,the results show:RLS has a shortcoming that the factor of SNR combination drops down when the antenna numbers of the array increases,while that of VSSLMS has nothing to do with the number of the array antennas;when the receiving signal is weak and the antenna number of the array is small,the performance of SNR combination of RLS is a little better than VSSLMS;But when the signal is strong especially when the antenna number of the array is big,the VSSLMS can obtain better performance of SNR combination.

antenna arraying;SNR combination performance;RLS algorithm;VSSLMS algorithm

10.3969/j.issn.1003-3106.2017.07.03

赵晓明,陈学军,魏瑞利,等.RLS、VSSLMS算法应用于天线组阵的分析及仿真[J].无线电工程,2017,47(7):10-14.[ZHAO Xiaoming,CHEN Xuejun,WEI Ruili,et al.Analysis and Simulation for RLS and VSSLMS used in Antenna Arraying,2017,47(7):10-14.]

2017-02-13

国家自然科学基金资助项目(61503414)。

TN850.9

A

1003-3106(2017)07-0010-05

赵晓明 男，(1971—)，硕士，高级工程师。主要研究方向：深空网天线组阵。

陈学军 男，(1968—)，硕士，高级工程师。主要研究方向：航天测控。