利用图像的动态性解决函数的综合问题
■河南省平顶山市第一中学 王丽娜 胡 玉
利用图像的动态性解决函数的综合问题
■河南省平顶山市第一中学 王丽娜 胡 玉
在每年高考试题当中,有关函数的试题都占有很大的比例。抽象性是函数问题的最大特点,如何寻找解决函数综合问题的切入点?本文结合实例,利用作图工具所作图像的动态性,通过形象的展示与动态的变化,帮助同学们深刻理解函数的概念和性质,以及函数图像的形成过程与应用。
一、利用图像的动态性求解分段函数的单调性

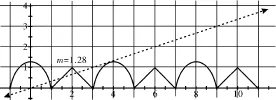
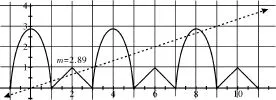
动态解析:当a从0开始变化时,函数f(x)的图像变化如图1~图5。满足条件:在(-∞,+∞)上是减函数的只有图2和图3,即满足 解得故选C。

图1
提炼:分段函数f(x)在整个定义域上单调递减必须从整体上考虑。不但要求在每一段上单调减,而且要求左半段的接点不低于右半段的接点,即整个函数图像从左到右必须一直下降(允许间断),借助图像的动态变化使问题“一目了然”。
二、利用图像的动态性求解函数图像的交点问题
已知函数f(x)= -x2+8x,g(x)=6lnx+m。是否存在实数 m,使得y=f(x)的图像与y=g(x)的图像有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,请说明理由。
动态解析:当m从小到大变化时,两条曲线的交点情况如图6~图10。当两条曲线在某个位置相切,此时为它们之间交点个数变化的临界位置,因此问题转化为求两条曲线相切时实数m的值。

图5
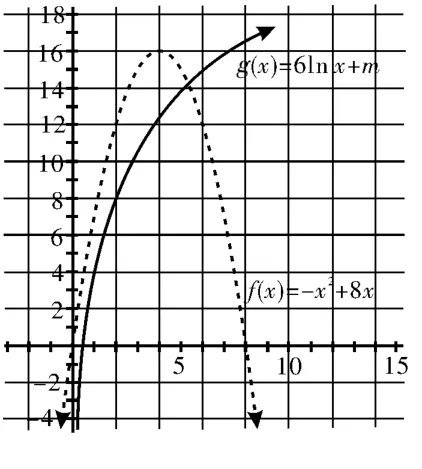
图6

图7
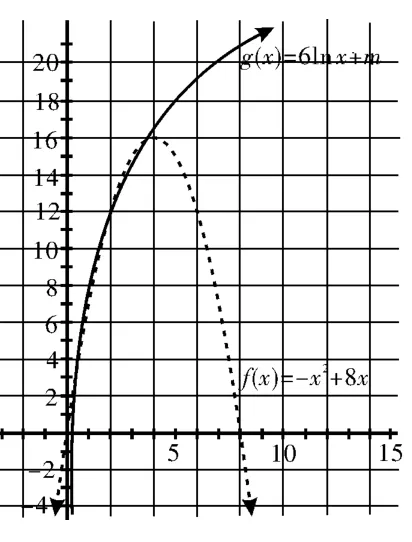
图8
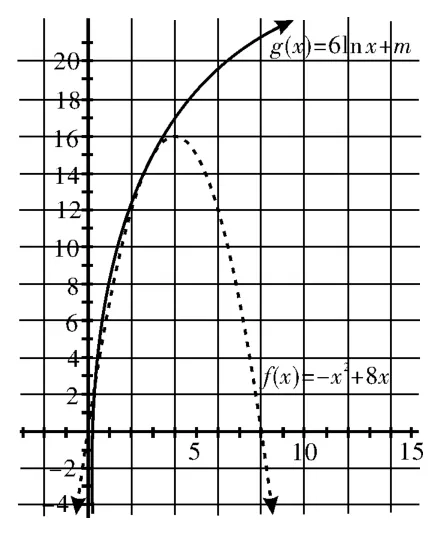
图9
当x=1时,f(x)与g(x)相切,如图7所示,由f(1)=g(1),解得m=7。
当x=3时,f(x)与g(x)相切,如图9所示,由f(3)=g(3),解得m=15-6ln3。

图10
当7 当m=7或m= 15-6ln3时,函数f(x)与g(x)的图像有两个不同的交点,如图7、9所示。 当m<7或m>15-6ln3时,函数f(x)与g(x)的图像有一个交点,如图6、10所示。 综上所述:当7 提炼:利用计算机作图工具可以帮助我们观察函数图像变化的过程及两个函数图像交点的变化规律,反过来帮助我们理解对数函数和二次函数的性质,以及它们之间的关系,使得数形结合有了更为广阔的用武之地。 图11 图12 图13 图14 图15 提炼:利用作图工具作出5类图像,寻求临界值,动态变换求得参数范围,凸显“形助数”的指导作用。对于周期函数来说,除了要掌握函数的整体性质,还需要抓住每个周期内的性质特征。在解决周期函数与非周期函数的综合问题时,研究两个函数关系发生改变的某个周期是解决问题的关键,可以避免大量烦琐的计算。 注:本文系2016年度河南省基础教育教学研究项目“信息技术辅助高中数学函数教学的应用研究”,课题编号:JCJYC16030453。 (责任编辑 王福华) 图2 图3 图4三、利用图像的动态性求解函数的零点或方程的根