关于运算律学习情况的调查和思考

浙江省衢州市衢江区全旺镇中心小学 陈建红 彭宝玉

一、缘起

在一次校级教研活动中上，我校的一位教师执教的是“乘法分配律”这一课时。听课教师感觉不错，在学生练习时（北师大版第49页第二题）其中有部分平时教师认为不错的学生，在解答中有三题出现了以下情况：

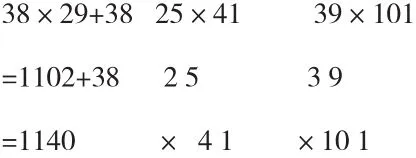
看到这里，笔者很困惑，学生的确是做对的，但我们教学运算定律的主要目标是让学生在计算中能依据题目数据特点进行简便计算。为什么有的学生在计算（20+4）×25、32×（200+3）、35×37+65×37时能运用乘法分配律进行简便计算，而对于38×29+38 、25×41、39×101却又用竖式计算了呢？为什么有的学生会出现（20+4）×25=20×25+4或（20+4）×25=20×25×4等错误呢？首先笔者为编写者所编排的这组习题叫好！应该说这组练习较全面的考查了学生对“乘法分配律”的灵活运用。结合自己的课堂教学，笔者也有这样的感觉：那就是尽管我们在教学中让学生充分体验乘法分配律的特征，可是最终一些学生在应用上还是存在各种各样的问题。是什么让这些学生难以致用呢？

二、运算律概述

“运算律”是小学数学“数的运算”中的一个重要内容，包括五个基本运算律，分别为：加法交换律a+b=b+a；加法结合律(a+b)+c=a+(b+c)；乘法交换律a×b=b×a；乘法结合律(a×b)×c=a×(b×c)；乘法分配律(a+b)×c=a×c+b×c。

三、对运算律学习情况的调查

1.孩子的想法

运算律的出现和运用使原本枯燥单调的计算活动变得充满灵活性、挑战性。提到学过的某个运算律，学生能够想到相应的字母公式，大多学生认为只要记住运算律的公式就能用来简便计算。同时不少学生也反应，记住公式比较容易，但在具体运用时，公式容易相混，特别是遇到变式题，判断不准用哪个公式、哪种方法，容易出错。

2.教师的认识

运算律是计算中最难啃的“骨头”之一，不像竖式计算和混合运算，只要掌握计算方法和运算顺序，加上细心认真，就能计算正确。令他们费解的是：在教学运算律的新授课上，学生反应良好，一般能较快地得出公式，也能运用公式进行简便计算，感觉难度不大。但在综合练习、变式练习时，由于运算律的题型变式多，易混题型多，学生很难分清，往往招架不住。

3.专家的看法

五个基本运算律从本质上反映了数学运算的规律，从形式到思想都具有高度的简洁性、概括性，是小学生最早接触或认识到的科学规律，在数学中具有重要的地位和作用。但是，当下运算律的教学可以说是处于被轻视的位置，教师对运算律的解读较浅，教材编写意图往往领略不到位，导致教学实况反馈不理想。

那么运算律应该怎样教学?如何才能让学生熟练正确运用运算律?运算律学习的最终目标又指向什么?事不避难，知难不难。笔者近几年对以上问题进行了一些思考与实践，力求突破这些难点，寻找到解决问题的有效策略。

四、解决策略及思考

1.重视运算律数学模型的建构

建构运算律的数学模型通常分以下几步：(1)从现实情境引出数学现象，感知运算律，体验它的合理性；(2)进行类似的实验，验证这种联系具有普遍性；(3)在观察、归纳、类比等学习活动中概括出运算律；(4)用字母符号抽象表示出运算律。

2.借“分类”思想，分辩各运算定律的运用

小学生由于年龄特征，思维往往表现出单一性，对复杂的事物一时也难以分辩。在学习乘法分配律之前，笔者发现学生都能很好的运用乘法的交换律和结合律进行简便计算。但是到了学习乘法分配律之后，很容易把乘法的结合律和分配律混肴，因此教师在教学中要充分利用习题资源借“分类”思想，促有效学习。

笔者认为：在计算课堂教学中，我们应根据教学内容的实际情况，经常进行这样的分类。俗话说“思之思之，神鬼通之”，这样的分类不仅能培养学生认真、仔细的学习习惯，还能培养他们的数学思考的习惯，更重要的是学生通过了这样的分类加深了知识之间的联系与比较，使学生发生错误的概率降低到最小化，让所学的知识较好的内化于学生。

3.依据学情.合理拓展

除了五个基本运算律外，我们往往进行一些推广，得到减法性质：a-b-c=a-(b+c)；除法性质：a÷b÷c=a÷(b×c)；这些性质可以通过解决现实问题的过程得以抽象，获得形式化，学生还是能够接受的。但是人为的增加像a-(b-c)=a-b+c、a÷(b÷c)：a÷b×c等运算符号加减混合、乘除混合的公式，往往由于没有经过验证，学生很难形成深刻印象，导致学生不但不能正确掌握，而且与其他公式相混。

顺便说一下，基本运算律之所以不涉及减法和除法运算，是因为在自然数集中，减法与除法运算不是封闭的，它们分别与加法与乘法互为逆运算。引入分数后，除法与乘法就可以统一为乘法；引入负数后，加法与减法就可以统一为加法。减法或除法的运算性质在数的理论系统中，不是源，只是流，因此与基本运算律不可等量齐观。

4.优化算法，培养思维灵活性

在数学学习的意义上，运算律教学的价值更多体现在应用上，它具有很强的工具性，即运算律是学生灵活处理运算程序、使运算过程简单但又不会改变运算结果的重要依据。“简便计算”是立足于“运算律”基础上的算法简单化的过程，学生可以根据运算和数据的特点，灵活选择运算方法，以提高运算的速度，从而培养思维的灵活性。

一个数学教师，如果不能对自己的学科怀有一种追本溯源的态度，如果不能对自己所教的数学有一份深切关注与深刻思索，他的工作则必然就带有一种盲目性与追逐性，自然就无法在纷繁复杂的数学教育变革中找准继承与创新的支点。